Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-03T04:57:56.463Z Has data issue: false hasContentIssue false
  • English
  • Français

Unstable miscible displacements in radial flow with chemical reactions

Published online by Cambridge University Press:  26 April 2021

Min Chan Kim ,
Satyajit Pramanik Open the ORCID record for Satyajit Pramanik [Opens in a new window] ,
Vandita Sharma Open the ORCID record for Vandita Sharma [Opens in a new window]  and
Manoranjan Mishra Open the ORCID record for Manoranjan Mishra [Opens in a new window]
Min Chan Kim
Affiliation:
Department of Chemical Engineering, Jeju National University, Jeju63243, Republic of Korea
Satyajit Pramanik*
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar382355, India
Vandita Sharma
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Rupnagar140001, India
Manoranjan Mishra
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Rupnagar140001, India
*
†Email address for correspondence: satyajit.pramanik@iitgn.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

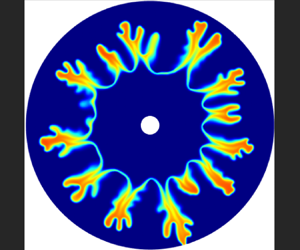
The effects of the $A + B \rightarrow C$ chemical reaction on miscible viscous fingering in a radial source flow are analysed using linear stability theory and numerical simulations. This flow and transport problem is described by a system of nonlinear partial differential equations consisting of Darcy's law for an incompressible fluid coupled with nonlinear advection–diffusion–reaction equations. For an infinitely large Péclet number ($Pe$), the linear stability equations are solved using spectral analysis. Further, the numerical shooting method is used to solve the linearized equations for various values of $Pe$ including the limit $Pe \rightarrow \infty$. In the linear analysis, we aim to capture various critical parameters for the instability using the concept of asymptotic instability, i.e. in the limit $\tau \rightarrow \infty$, where $\tau$ represents the dimensionless time. We restrict our analysis to the asymptotic limit $Da^{\ast }$$(= Da \tau ) \rightarrow \infty$ and compare the results with the non-reactive case ($Da = 0$) for which $Da^{\ast } = 0$, where $Da$ is the Damköhler number. In the latter case, the dynamics is controlled by the dimensionless parameter $R_{Phys} = -(R_{A} - \beta R_{B})$. In the former case, for a fixed value of $R_{Phys}$, the dynamics is determined by the dimensionless parameter $R_{Chem} = -(R_{C} - R_{B} - R_{A})$. Here, $\beta$ is the ratio of reactants’ initial concentration and $R_{A}$, $R_{B}$ and $R_{C}$ are the log-viscosity ratios. We perform numerical simulations of the coupled nonlinear partial differential equations for large values of $Da$. The critical values $R_{Phys, c}$ and $R_{Chem, c}$ for instability decrease with $Pe$ and they exhibit power laws in $Pe$. In the asymptotic limit of infinitely large $Pe$ they exhibit a power-law dependence on $Pe$ ($R_{Chem, c} \sim Pe^{-1/2}$ as $Pe \rightarrow \infty$) in both the linear and nonlinear regimes.

JFM classification

Interfacial Flows (free surface): Fingering instability Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 917 , 25 June 2021 , A25
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Al-Gwaiz, M.A. 2008 Sturm-Liouville Theory and its Applications. Springer-Verlag.Google Scholar
Balog, E., Bittmann, K., Schwarzenberger, K., Eckert, K., De Wit, A. & Schuszter, G. 2019 Influence of microscopic precipitate structures on macroscopic pattern formation in reactive flows in a confined geometry. Phys. Chem. Chem. Phys. 21, 2910–2918.CrossRefGoogle Scholar
Ben, Y., Demekhin, E.A. & Chang, H.-C. 2002 A spectral theory for small-amplitude miscible fingering. Phys. Fluids 14 (3), 999–1010.10.1063/1.1446885CrossRefGoogle Scholar
Brau, F. & De Wit, A. 2020 Influence of rectilinear vs radial advection on the yield of $A + B \rightarrow C$ reaction fronts: a comparison. J. Chem. Phys. 152 (5), 054716.CrossRefGoogle Scholar
Brau, F., Schuszter, G. & De Wit, A. 2017 Flow control of $A+B\rightarrow C$ fronts by radial injection. Phys. Rev. Lett. 118, 134101.10.1103/PhysRevLett.118.134101CrossRefGoogle Scholar
Campana, D.M. & Carvalho, M.S. 2014 Liquid transfer from single cavities to rotating rolls. J. Fluid Mech. 747, 545–571.10.1017/jfm.2014.175CrossRefGoogle Scholar
Cardenas, M.B., et al. 2019 Submarine groundwater and vent discharge in a volcanic area associated with coastal acidification. Geophys. Res. Lett. e2019GL085730.Google Scholar
Chandrasekhar, S. 2013 Hydrodynamic and Hydromagnetic Stability. Courier Corporation.Google Scholar
Chung, D.-W., Shearing, P.R., Brandon, N.P., Harris, S.J. & García, R.E. 2014 Particle size polydispersity in Li-ion batteries. J. Electrochem. Soc. 161 (3), A422–A430.10.1149/2.097403jesCrossRefGoogle Scholar
COMSOL 2019 v. 5.4 COMSOL AB.Google Scholar
Davit, Y., Byrne, H., Osborne, J., Pitt-Francis, J., Gavaghan, D. & Quintard, M. 2013 Hydrodynamic dispersion within porous biofilms. Phys. Rev. E 87 (1), 012718.10.1103/PhysRevE.87.012718CrossRefGoogle ScholarPubMed
De Wit, A. 2016 Chemo-hydrodynamic patterns in porous media. Phil. Trans. R. Soc. A 374 (2078), 20150419.10.1098/rsta.2015.0419CrossRefGoogle ScholarPubMed
De Wit, A. 2020 Chemo-hydrodynamic patterns and instabilities. Annu. Rev. Fluid Mech. 52, 531–555.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 2004 Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Escala, D.M., De Wit, A., Carballido-Landeira, J. & Muñuzuri, A.P. 2019 Viscous fingering induced by a pH-sensitive clock reaction. Langmuir 35 (11), 4182–4188.10.1021/acs.langmuir.8b03834CrossRefGoogle ScholarPubMed
Gérard, T. & De Wit, A. 2009 Miscible viscous fingering induced by a simple $A + B \rightarrow C$ chemical reaction. Phys. Rev. E 79 (1), 016308.10.1103/PhysRevE.79.016308CrossRefGoogle Scholar
Hejazi, S.H., Trevelyan, P.M.J., Azaiez, J. & De Wit, A. 2010 Viscous fingering of a miscible reactive $a+ b \rightarrow c$ interface: a linear stability analysis. J. Fluid Mech. 652, 501–528.CrossRefGoogle Scholar
Hill, S. 1952 Channeling in packed columns. Chem. Engng Sci. 1 (6), 247–253.CrossRefGoogle Scholar
Homsy, G.M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.CrossRefGoogle Scholar
Huppert, H.E. & Neufeld, J.A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46 (1), 255–272.CrossRefGoogle Scholar
Kim, M.C. 2012 Onset of radial viscous fingering in a Hele-Shaw cell. Korean J. Chem. Engng 29 (12), 1688–1694.10.1007/s11814-012-0091-3CrossRefGoogle Scholar
Kim, M.C. 2014 Effect of the irreversible $A + B \rightarrow C$ reaction on the onset and the growth of the buoyancy-driven instability in a porous medium. Chem. Engng Sci. 112, 56–71.CrossRefGoogle Scholar
Kim, M.C. 2018 Double diffusive effects on radial fingering in a porous medium or a Hele-Shaw cell. Korean J. Chem. Engng 35 (2), 364–374.CrossRefGoogle Scholar
Kim, M.C. & Choi, C.K. 2011 The stability of miscible displacement in porous media: nonmonotonic viscosity profiles. Phys. Fluids 23 (8), 084105.10.1063/1.3624620CrossRefGoogle Scholar
Kumar, A. & Mishra, M. 2019 Boundary effects on the onset of miscible viscous fingering in a Hele-Shaw flow. Phys. Rev. Fluids 4, 104004.CrossRefGoogle Scholar
Lerisson, G., Ledda, P.G., Balestra, G. & Gallaire, F. 2020 Instability of a thin viscous film flowing under an inclined substrate: steady patterns. J. Fluid Mech. 898, A6.CrossRefGoogle Scholar
Mcdowell, A., Zarrouk, S.J. & Clarke, R. 2016 Modelling viscous fingering during reinjection in geothermal reservoirs. Geothermics 64, 220–234.CrossRefGoogle Scholar
Nagatsu, Y & De Wit, A. 2011 Viscous fingering of a miscible reactive $A+B \rightarrow C$ interface for an infinitely fast chemical reaction: nonlinear simulations. Phys. Fluids 23 (4), 043103.CrossRefGoogle Scholar
Nagatsu, Y., Ishii, Y., Tada, Y. & De Wit, A. 2014 Hydrodynamic fingering instability induced by a precipitation reaction. Phys. Rev. Lett. 113, 024502.CrossRefGoogle ScholarPubMed
Nagatsu, Y., Matsuda, K., Kato, Y. & Tada, Y. 2007 Experimental study on miscible viscous fingering involving viscosity changes induced by variations in chemical species concentrations due to chemical reactions. J. Fluid Mech. 571, 475–493.10.1017/S0022112006003636CrossRefGoogle Scholar
Nama, N., Huang, T.J. & Costanzo, F. 2017 Acoustic streaming: an arbitrary Lagrangian–Eulerian perspective. J. Fluid Mech. 825, 600–630.CrossRefGoogle ScholarPubMed
Nejati, I., Dietzel, M. & Hardt, S. 2015 Conjugated liquid layers driven by the short-wavelength Bénard–Marangoni instability: experiment and numerical simulation. J. Fluid Mech. 783, 46–71.CrossRefGoogle Scholar
Paterson, L. 1981 Radial fingering in a Hele Shaw cell. J. Fluid Mech. 113, 513–529.CrossRefGoogle Scholar
Pritchard, D. 2004 The instability of thermal and fluid fronts during radial injection in a porous medium. J. Fluid Mech. 508, 133–163.10.1017/S0022112004009000CrossRefGoogle Scholar
Rana, C., Pramanik, S., Martin, M., De Wit, A & Mishra, M. 2019 Influence of langmuir adsorption and viscous fingering on transport of finite size samples in porous media. Phys. Rev. Fluids 4 (10), 104001.CrossRefGoogle Scholar
Riaz, A. & Meiburg, E. 2003 a Radial source flows in porous media: linear stability analysis of axial and helical perturbations in miscible displacements. Phys. Fluids 15 (4), 938–946.CrossRefGoogle Scholar
Riaz, A. & Meiburg, E. 2003 b Three-dimensional miscible displacement simulations in homogeneous porous media with gravity override. J. Fluid Mech. 494, 95–117.CrossRefGoogle Scholar
Riaz, A., Pankiewitz, C. & Meiburg, E. 2004 Linear stability of radial displacements in porous media: influence of velocity-induced dispersion and concentration-dependent diffusion. Phys. Fluids 16 (10), 3592–3598.CrossRefGoogle Scholar
Saffman, P.G. & Taylor, G.I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A Math. Phys. Sci. 245 (1242), 312–329.Google Scholar
Schuszter, G., Brau, F. & De Wit, A. 2016 a Calcium carbonate mineralization in a confined geometry. Environ. Sci. Technol. Lett. 3 (4), 156–159.CrossRefGoogle Scholar
Schuszter, G., Brau, F. & De Wit, A. 2016 b Flow-driven control of calcium carbonate precipitation patterns in a confined geometry. Phys. Chem. Chem. Phys. 18, 25592–25600.CrossRefGoogle Scholar
Schuszter, G. & De Wit, A. 2016 Comparison of flow-controlled calcium and barium carbonate precipitation patterns. J. Chem. Phys. 145 (22), 224201.CrossRefGoogle ScholarPubMed
Sharma, V., Nand, S., Pramanik, S., Chen, C.-Y. & Mishra, M. 2020 Control of radial miscible viscous fingering. J. Fluid Mech. 884, A16.10.1017/jfm.2019.932CrossRefGoogle Scholar
Sharma, V., Pramanik, S., Chen, C.-Y. & Mishra, M. 2019 A numerical study on reaction-induced radial fingering instability. J. Fluid Mech. 862, 624–638.10.1017/jfm.2018.963CrossRefGoogle Scholar
Sharma, V., Pramanik, S. & Mishra, M. 2016 Fingering instabilities in variable viscosity miscible fluids: radial source flow. In Proceedings of the 2016 COMSOL Conference in Bangalore.Google Scholar
Sharma, V., Pramanik, S. & Mishra, M. 2017 Dynamics of a highly viscous circular blob in homogeneous porous media. Fluids 2 (4), 32.CrossRefGoogle Scholar
Tan, C.T. & Homsy, G.M. 1987 Stability of miscible displacements in porous media: radial source flow. Phys. Fluids 30 (5), 1239–1245.CrossRefGoogle Scholar
Tóth, Á., Schuszter, G., Das, N.P., Lantos, E., Horváth, D., De Wit, A. & Brau, F. 2020 Effects of radial injection and solution thickness on the dynamics of confined $A + B \rightarrow C$ chemical fronts. Phys. Chem. Chem. Phys. 22 (18), 10278–10285.CrossRefGoogle Scholar
Trevelyan, P.M.J. & Walker, A.J. 2018 Asymptotic properties of radial $A+B \rightarrow C$ reaction fronts. Phys. Rev. E 98, 032118.CrossRefGoogle Scholar
Welty, C., Kane, A.C. & Kauffman, L.J. 2003 Stochastic analysis of transverse dispersion in density-coupled transport in aquifers. Water Resour. Res. 39 (6), 1150.CrossRefGoogle Scholar
Yortsos, Y.C. 1987 Stability of displacement processes in porous media in radial flow geometries. Phys. Fluids 30 (10), 2928–2935.10.1063/1.866070CrossRefGoogle Scholar