Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-31T11:44:44.359Z Has data issue: false hasContentIssue false
  • English
  • Français

Added-mass force on elliptic airfoils

Published online by Cambridge University Press:  10 September 2021

Eric J. Limacher Open the ORCID record for Eric J. Limacher [Opens in a new window]
Eric J. Limacher*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: limacher@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

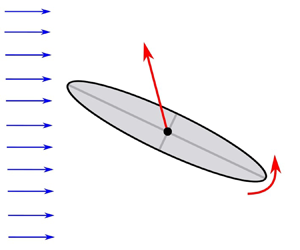
Herein, exact algebraic expressions for the non-circulatory (added-mass) forces on elliptic airfoils are derived for any two-dimensional motion – including simultaneous rectilinear acceleration and rotation – embedded in a steady free-stream flow. Despite the lengthy history of the added-mass concept and its widespread application to cylinders of various cross-sections, such closed-form expressions for elliptic cylinders, in terms of kinematic and geometric parameters alone, have remained absent from the literature until now. Inspection of the derived equations reveals that for pure pitching about a point on the chord-line, increasing thickness always decreases the added-mass force magnitude. For any given motion of the chord-line, the difference in force between thick and thin airfoils is proportional to the square of the thickness, although this difference may be positive or negative for the general three-degree-of-freedom case. In the special case of zero thickness and small pitch angles, Theodorsen's added-mass lift force on rigid thin airfoils is recovered; for large pitch angles, an exact generalization of Theodorsen's expression, applicable to the chord-normal direction, is given.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 926 , 10 November 2021 , R2
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brennen, C.E. 1982 A review of added mass and fluid inertial forces. Tech. Rep. N62583-81-MR-554. Naval Civil Engineering Laboratory.Google Scholar
Chang, C.-C. 1992 Potential flow and forces for incompressible viscous flow. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 437 (1901), 517–525.Google Scholar
Fackrell, S. 2011 Study of the added mass of cylinders and spheres. PhD thesis, University of Windsor.Google Scholar
Fernandez-Feria, R. 2019 On the added-mass force and moment and the vortex projection method. Application to thin airfoils. Fluid Dyn. Res. 51 (3), 035509.CrossRefGoogle Scholar
von Kármán, T. & Sears, W.R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5 (10), 379–390.CrossRefGoogle Scholar
Kinsey, T. & Dumas, G. 2008 Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 46 (6), 1318–1330.CrossRefGoogle Scholar
La Mantia, M. & Dabnichki, P. 2012 Added mass effect on flapping foil. Engng Anal. Bound. Elem. 36 (4), 579–590.CrossRefGoogle Scholar
Lighthill, J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
Limacher, E.J. 2019 Added mass and vortical impulse: theory and experiment. PhD thesis, University of Calgary.Google Scholar
Limacher, E., Morton, C. & Wood, D. 2018 Generalized derivation of the added-mass and circulatory forces for viscous flows. Phys. Rev. Fluids 03, 014701.CrossRefGoogle Scholar
Milne-Thomson, L.M. 1968 Theoretical hydrodynamics, 5th ed. MacMillan Education Ltd.CrossRefGoogle Scholar
Newman, J.N. 1977 Marine hydrodynamics. MIT Press.CrossRefGoogle Scholar
Ōtomo, S., Henne, S., Mulleners, K., Ramesh, K. & Viola, I.M. 2021 Unsteady lift on a high-amplitude pitching aerofoil. Exp. Fluids 62 (1), 6.CrossRefGoogle Scholar
Polet, D.T., Rival, D.E. & Weymouth, G.D. 2015 Unsteady dynamics of rapid perching manoeuvres. J. Fluid Mech. 767, 323–341.CrossRefGoogle Scholar
Quartapelle, L. & Napolitano, M. 1983 Force and moment in incompressible flows. AIAA J. 21 (6), 911–913.CrossRefGoogle Scholar
Saffman, P.G. 1992 Vortex dynamics. Cambridge University Press.Google Scholar
Sedov, L.I. 1965 Two-dimensional problems in hydrodynamics and aerodynamics. Interscience Publishers (John Wiley and Sons Inc.).CrossRefGoogle Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. Tech. Rep. 496. National Advisory Committee for Aeronautics.Google Scholar
Van Buren, T., Floryan, D. & Smits, A.J. 2019 Scaling and performance of simultaneously heaving and pitching foils. AIAA J. 57 (9), 3666–3677. arXiv:1801.07625.CrossRefGoogle Scholar
Williamson, C.H.K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Wu, J.C. 1981 Theory for aerodynamic force and moment in viscous flows. AIAA J. 19 (4), 432–441.CrossRefGoogle Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2015 Vortical flows. Springer.CrossRefGoogle Scholar