Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hooke, John A.
1970.
On some limit theorems for the GI/G/1 queue.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
634.
Whitt, Ward
1970.
Multiple channel queues in heavy traffic. III: random server selection.
Advances in Applied Probability,
Vol. 2,
Issue. 2,
p.
370.
Iglehart, Donald L.
and
Kennedy, Douglas P.
1970.
Weak convergence of the average of flag processes.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
747.
Iglehart, Donald L.
1971.
Functional limit theorems for the queue GI/G/1 in light traffic.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
269.
Kyprianou, E.
1971.
The virtual waiting time of the GI/G/1 queue in heavy traffic.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
249.
Whitt, Ward
1971.
Weak convergence theorems for priority queues: preemptive-resume discipline.
Journal of Applied Probability,
Vol. 8,
Issue. 01,
p.
74.
Iglehart, Donald L.
1971.
Multiple channel queues in heavy traffic.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 17,
Issue. 2,
p.
168.
Cohen, J. W.
1972.
The suprema of the actual and virtual waiting times during a busy cycle of the Km/Kn/1 queueing system.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
339.
Cohen, J. W.
1972.
The suprema of the actual and virtual waiting times during a busy cycle of the K
m/K
n/1 queueing system.
Advances in Applied Probability,
Vol. 4,
Issue. 02,
p.
339.
Kennedy, Douglas P.
1972.
Rates of convergence for queues in heavy traffic. II: Sequences of queueing systems.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
382.
Kennedy, Douglas P.
1972.
Rates of convergence for queues in heavy traffic. I.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
357.
Whitt, Ward
1972.
Complements to heavy traffic limit theorems for the GI/G/1 queue.
Journal of Applied Probability,
Vol. 9,
Issue. 01,
p.
185.
Harrison, J. Michael
1973.
A limit theorem for priority queues in heavy traffic.
Journal of Applied Probability,
Vol. 10,
Issue. 04,
p.
907.
Loulou, Richard
1973.
Multi-channel queues in heavy traffic.
Journal of Applied Probability,
Vol. 10,
Issue. 4,
p.
769.
Kennedy, Douglas P.
1973.
Limit theorems for finite dams.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 3,
p.
269.
Iglehart, Donald L.
1973.
Weak convergence of compound stochastic process, I.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 1,
p.
11.
Cohen, J.W.
1973.
Asymptotic relations in queueing theory.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 2,
p.
107.
Crane, Michael A.
1973.
Queues in transportation systems, I: a Markovian system.
Journal of Applied Probability,
Vol. 10,
Issue. 3,
p.
630.
Iglehart, Donald L.
1973.
Weak convergence in queueing theory.
Advances in Applied Probability,
Vol. 5,
Issue. 3,
p.
570.
Loulou, Richard
1973.
Multi-channel queues in heavy traffic.
Journal of Applied Probability,
Vol. 10,
Issue. 4,
p.
769.
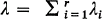 is the total arrival rate to the system and
is the total arrival rate to the system and 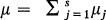 is the maximum service rate of the system. As a measure of congestion we define the traffic intensity ρ = λ/μ.
is the maximum service rate of the system. As a measure of congestion we define the traffic intensity ρ = λ/μ.



