Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mather, John N.
1984.
Amount of rotation about a point and the Morse index.
Communications in Mathematical Physics,
Vol. 94,
Issue. 2,
p.
141.
MacKay, R. S.
and
Percival, I. C.
1985.
Converse KAM: Theory and practice.
Communications in Mathematical Physics,
Vol. 98,
Issue. 4,
p.
469.
Escande, D.F.
1985.
Stochasticity in classical Hamiltonian systems: Universal aspects.
Physics Reports,
Vol. 121,
Issue. 3-4,
p.
165.
Chou, Weiren
and
Griffiths, Robert B.
1986.
Ground states of one-dimensional systems using effective potentials.
Physical Review B,
Vol. 34,
Issue. 9,
p.
6219.
Jürgen, Moser
1986.
Recent Developments in the Theory of Hamiltonian Systems.
SIAM Review,
Vol. 28,
Issue. 4,
p.
459.
Mather, John
1986.
A criterion for the non-existence of invariant circles.
Publications mathématiques de l'IHÉS,
Vol. 63,
Issue. 1,
p.
153.
MacKay, R. S.
1986.
Lecture Notes in Physics.
Vol. 247,
Issue. ,
p.
390.
Leage, I.
and
Mackay, R.S.
1986.
Badly ordered periodic orbits of the standard map.
Physics Letters A,
Vol. 118,
Issue. 6,
p.
274.
Yamaguchi, Yoshihiro
1986.
Breakup of an invariant curve in a dissipative standard mapping.
Physics Letters A,
Vol. 116,
Issue. 7,
p.
307.
Moser, Jürgen
1986.
Lecture Notes in Physics.
Vol. 247,
Issue. ,
p.
492.
Bangert, V.
1987.
The existence of gaps in minimal foliations.
Aequationes Mathematicae,
Vol. 34,
Issue. 2-3,
p.
153.
Boyland, Philip L.
and
Hall, Glen Richard
1987.
Invariant circles and the order structure of periodic orbits in monotone twist maps.
Topology,
Vol. 26,
Issue. 1,
p.
21.
Olvera, Arturo
and
Simó, Carles
1987.
An obstruction method for the destruction of invariant curves.
Physica D: Nonlinear Phenomena,
Vol. 26,
Issue. 1-3,
p.
181.
Paramio, M.
and
Sesma, J.
1987.
Breakdown of KAM tori in the standard map.
Physics Letters A,
Vol. 124,
Issue. 6-7,
p.
345.
Boyland, Philip L.
1987.
Invariant circles and rotation bands in monotone twist maps.
Communications in Mathematical Physics,
Vol. 113,
Issue. 1,
p.
67.
Barge, Marcy
and
Swanson, Richard
1988.
Rotation shadowing properties of circle and annulus maps.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 4,
p.
509.
Stark, J.
1988.
An exhaustive criterion for the non-existence of invariant circles for area-preserving twist maps.
Communications in Mathematical Physics,
Vol. 117,
Issue. 2,
p.
177.
Celletti, Alessandra
and
Chierchia, Luigi
1988.
Construction of analytic KAM surfaces and effective stability bounds.
Communications in Mathematical Physics,
Vol. 118,
Issue. 1,
p.
119.
Eckhardt, Bruno
1988.
Quantum mechanics of classically non-integrable systems.
Physics Reports,
Vol. 163,
Issue. 4,
p.
205.
1988.
Destruction of invariant circles.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 8,
p.
199.




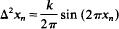
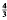 .
.