Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T00:59:37.664Z Has data issue: false hasContentIssue false
  • English
  • Français

A TWO-CLASS RETRIAL SYSTEM WITH COUPLED ORBIT QUEUES

Published online by Cambridge University Press:  23 January 2017

Ioannis Dimitriou
Ioannis Dimitriou*
Affiliation:
Department of Mathematics, University of Patras, 26500 Patras, Greece E-mail: idimit@math.upatras.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a single server system accepting two types of retrial customers, which arrive according to two independent Poisson streams. The service station can handle at most one customer, and in case of blocking, type i customer, i=1, 2, is routed to a separate type i orbit queue of infinite capacity. Customers from the orbits try to access the server according to the constant retrial policy. We consider coupled orbit queues, and thus, when both orbit queues are non-empty, the orbit queue i tries to re-dispatch a blocked customer of type i to the main service station after an exponentially distributed time with rate μi. If an orbit queue empties, the other orbit queue changes its re-dispatch rate from μi to 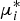$\mu_{i}^{\ast}$. We consider both exponential and arbitrary distributed service requirements, and show that the probability generating function of the joint stationary orbit queue length distribution can be determined using the theory of Riemann (–Hilbert) boundary value problems. For exponential service requirements, we also investigate the exact tail asymptotic behavior of the stationary joint probability distribution of the two orbits with either an idle or a busy server by using the kernel method. Performance metrics are obtained, computational issues are discussed and a simple numerical example is presented.

Keywords

asymptotic analysisboundary value problemscoupled orbit queuesretrials
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 31 , Issue 2 , April 2017 , pp. 139 - 179
Copyright
Copyright © Cambridge University Press 2017 

References

1. Adan, I., Boxma, O., Kapodistria, S., & Kulkarni, V. (2016). The shortest queue polling model. Annals of Operations Research 241(1): 167–200.Google Scholar
2. Andradottir, S., Ayhan, H., & Down, D. (2001). Server assignment policies for maximizing the steady-state throughput of finite queueing systems. Management Science 47: 1421–1439.Google Scholar
3. Artalejo, J.R. (1999). A classified bibliography of research on retrial queues: progress in 1990–1999. Top 7: 187–211.Google Scholar
4. Artalejo, J.R. (1999). Accessible bibliography on retrial queues. Mathematical and Computer Modeling 30: 1–6.Google Scholar
5. Artalejo, J.R. & Gomez-Corral, A. (2008). Retrial queueing systems: a computational approach. Berlin: Springer-Verlag.Google Scholar
6. Artalejo, J.R. (1997). Analysis of an M/G/1 queue with constant repeated attempts and server vacations. Computers and Operations Research 24(6): 493–504.Google Scholar
7. Avrachenkov, K., Nain, P., & Yechiali, U. (2014). A retrial system with two input streams and two orbit queues. Queueing Systems 77: 1–31.Google Scholar
8. Avrachenkov, K. & Yechiali, U. (2010). Retrial networks with finite buffers and their applications to internet data traffic. Probability in the Engineering and Informational Sciences 22: 519–536.Google Scholar
9. Badila, S. & Resing, J.A.C. (2016). A coupled processor model with simultaneous arrivals and ordered service requirements. Queueing Systems 82: 29–42.Google Scholar
10. Borst, S., Boxma, O., & Uitert, M. (2003). The asymptotic workload behavior of two coupled queues. Queueing Systems 43(1–2): 81–102.Google Scholar
11. Borst, S., Boxma, O., & Jelenkovic, P. (2000). Coupled processors with regularly varying service times. In INFOCOM 2000 Proceedings, IEEE, vol. 1, pp. 157–164.Google Scholar
12. Borst, S., Jonckheere, M., & Leskela, L. (2008). Stability of parallel queueing systems with coupled service rates. Discrete Event Dynamic Systems 18(4): 447–472.Google Scholar
13. Borst, , Hegde, S., & Proutiere, A. (2009). Interacting queues with server selection and coordinated scheduling: application to cellular data networks. Annals of Operations Research 170(1): 59–78.Google Scholar
14. Boxma, O. & Groenendijk, W.P. (1988). Two queues with alternating service and switching times. In Boxma, O. & Syski, R. (eds.), Queueing theory and its applications. Amsterdam: North-Holland, pp. 261–281.Google Scholar
15. Boxma, O. (1984). Two symmetric queues with alternating service and switching times. In Gelenbe, E. (ed.), Performance ’84. Amsterdam: North-Holland, pp. 409–431.Google Scholar
16. Cohen, J.W. (1982). The single server queue. Amsterdam: North-Holland.Google Scholar
17. Cohen, J.W. & Boxma, O. (1983). Boundary value problems in queueing systems analysis. Amsterdam: North-Holland.Google Scholar
18. Cohen, J.W. (1987). A two queue, one server model with priority for the longer queue. Queueing Systems 2: 261–283.Google Scholar
19. Cohen, J.W. (1988). Boundary value problems in queueing theory. Queueing Systems 3: 97–128.Google Scholar
20. Cohen, J.W. (1992). Analysis of random walks. Amsterdam: I.O.S. Press.Google Scholar
21. Choi, B.D., Park, K.K., & Pearce, C.E.M. (1993). The M/M/1 retrial queue with control policy and general retrial times. Queueing Systems 14: 275–292.Google Scholar
22. Choi, B.D., Rhee, K. H., & Park, K.K. (1993). The M/G/1 retrial queue with retrial rate control policy. Probability in the Engineering and Informational Sciences 7: 29–46.Google Scholar
23. Denteneer, D. & van Leeuwaarden, J.S.H. (2008). Multiaccess, Reservations & Queues. Philips Research Book Series, vol. 10, Heidelberg, Berlin: Springer-Verlag.Google Scholar
24. Dimitriou, I. (2016). A queueing model with two types of retrial customers and paired services. Annals of Operations Research 238(1): 123–143.Google Scholar
25. Falin, G.I. & Templeton, J.G.C. (1997). Retrial queues. London: Chapman & Hall.Google Scholar
26. Falin, G.I. (1988). On a multiclass batch arrival retrial queue. Advances in Applied Probability 20: 483–487.Google Scholar
27. Farahmand, K. (1990). Single line queue with repeated demands. Queueing Systems 6: 223–228.Google Scholar
28. Fayolle, G. (1986). A simple telephone exchange with delayed feedbacks. In Boxma, O.J., Cohen, J.W. & Tijms, M.C. (eds.), Proceedings of the International Conference on Teletraffic Analysis and Computer Performance Evaluation. Amsterdam: North-Holland, pp. 245–253.Google Scholar
29. Fayolle, G. & Iasnogorodski, R. (1979). Two coupled processors: The reduction to a Riemann–Hilbert problem. Zeitschrift fur Wahrscheinlichkeitstheorie und Verwandte Gebiete 47: 325–351.Google Scholar
30. Fayolle, G., Iasnogorodski, R., & Malyshev, V. (1999). Random walks in the quarter-plane, algebraic methods, boundary value problems and applications. Vol. 40 of Applications of Mathematics. Berlin: Springer-Verlag.Google Scholar
31. Feng, W., Kowada, M., & Adachi, K. (1998). A two-queue model with Bernoulli service schedule and switching times. Queueing Systems 30: 405–434.Google Scholar
32. Flajolet, F. & Sedgewich, R. (2009). Analytic combinatorics. New York: Cambridge University Press.Google Scholar
33. Gakhov, F.D. (1966). Boundary value problems. Oxford: Pergamon Press.Google Scholar
34. Grishechkin, S.A. (1992). Multiclass batch arrival retrial queues analyzed as branching processes with immigration. Queueing Systems 11: 395–418.Google Scholar
35. Guillemin, F. & van Leeuwaarden, J.H.S. (2011). Rare event asymptotics for a random walk in the quarter plane. Queueing Systems 67: 1–32.Google Scholar
36. Guillemin, F. & Pinchon, D. (2004). Analysis of generalized processor-sharing systems with two classes of customers and exponential services. Journal of Applied Probability 41: 832–858.Google Scholar
37. Hunter, T.E. & Nosratinia, A. (2004). Diversity through coded cooperation. IEEE Transactions on Wireless Communications 5: 283–289.CrossRefGoogle Scholar
38. Janssens, G.K. (1997). The quasi-random input queueing system with repeated attempts as a model for a collision-avoidance star local area network. IEEE Transactions on Communications 45: 360–364.Google Scholar
39. Khomichkov, I.I. (1995). Calculation of the characteristics of local area network with p-persistent protocol of multiple random access. Automation and Remote Control 56: 208–218.Google Scholar
40. Kulkarni, V.G. (1986). Expected waiting times in a multiclass batch arrival retrial queue. Journal of Applied Probability 23: 144–154.Google Scholar
41. Langaris, C. & Dimitriou, I. (2010). A queueing system with n-phases of service and (n-1)-types of retrial customers. European Journal of Operations Research 205: 638–649.Google Scholar
42. Li, H. & Zhao, Y.Q. (2011). Tail asymptotics for a generalized two-demand queuing model-a kernel method. Queueing Systems 69: 77–100.Google Scholar
43. Li, H. & Zhao, Y.Q. (2015). A kernel method for exact tail asymptotics for random walks in the quarter plane. http://arxiv.org/pdf/1505.04425v1.pdf Google Scholar
44. Moutzoukis, E. & Langaris, C. (1996). Non-preemptive priorities and vacations in a multiclass retrial queueing system. Stochastic Models 12(3): 455–472.Google Scholar
45. Muskhelishvili, N.I. (1992). Singular integral equations. New York: Dover Publications.Google Scholar
46. Nain, P. (1985). Analysis of a two-node Aloha network with infinite capacity buffers. In Hasegawa, T., Takagi, H. & Takahashi, Y. (eds.), Proceedings of the International Seminar on Computer Networking and Performance Evaluation. Tokyo, Japan, pp. 49–63.Google Scholar
47. Nehari, Z. (1975). Conformal mapping. New York: Dover Publications.Google Scholar
48. Papadimitriou, G., Pappas, N., Traganitis, A., & Angelakis, V. (2015). Network-level performance evaluation of a two-relay cooperative random access wireless system. Computer Networks 88: 187–201.Google Scholar
49. Pappas, N., Kountouris, M., Ephremides, A., & Traganitis, A. (2015). Relay-assisted multiple access with full-duplex multi-packet reception. IEEE Transactions on Wireless Communications 14: 3544–3558.Google Scholar
50. Resing, J.A.C. & Ormeci, L. (2003). A tandem queueing model with coupled processors. Operations Research Letters 31: 383–389.Google Scholar
51. Rengarajan, B., Caramanis, C., & De Veciana, G. (2008). Analyzing queueing systems with coupled processors through semi definite programming. INFORMS: Applied Probability Session, http://users.ece.utexas.edu/gustavo/papers/SdpCoupledQs.pdf Google Scholar
52. Song, Y., Liu, Z., & Zhao, Y. (2016). Exact tail asymptotics: revisit of a retrial queue with two input streams and two orbits. Annals of Operations Research 247: 97–120.Google Scholar
53. Szpankowski, W. (1994). Stability conditions for some multiqueue distributed systems: Buffered random access systems. Advances in Applied Probability 26: 498–515.Google Scholar
54. Takahashi, Y. (1990). Coupled processor: a second order continuous state model. Probability in the Engineering and Informational Sciences 4: 277–298.Google Scholar
55. Van Leeuwaarden, J.S.H., & Resing, J.A.C. (2005). A tandem queue with coupled processors: Computational issues. Queueing Systems 50: 29–52.Google Scholar
56. Vitale, C., Rizzo, G., Rengarajan, B., & Mancuso, V. (2015). An analytical approach to performance analysis of coupled processor systems. ITC 2015 Proceedings of 27th International Teletraffic Congress, IEEE, Ghent, Belgium, pp. 89–97.Google Scholar
57. Vitale, C, Rizzo, G., & Mancuso, V. (2015). A coupled processors model for 802.11 ad hoc networks under non saturation. In ICC 2015, IEEE International Conference on Communications, London, UK, pp. 628–634.Google Scholar
58. Vitale, C, Mancuso, V., & Rizzo, G. (2015). Modelling D2D communications in cellular access networks via coupled processors. COMSNETS 2015 Proceedings of 7th International Conference on Communication Systems and Networks, Bangalore, India, pp. 1–8.Google Scholar