Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-02T21:48:52.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermal plumes in viscoplastic fluids: flow onset and development

Published online by Cambridge University Press:  18 December 2015

I. Karimfazli ,
I. A. Frigaard  and
A. Wachs
I. Karimfazli
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC, V6T 1Z4, Canada
I. A. Frigaard*
Affiliation:
Department of Mechanical Engineering, University of British Columbia, 2054-6250 Applied Science Lane, Vancouver, BC, V6T 1Z4, Canada Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada
A. Wachs
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2, Canada IFP Energies nouvelles, Fluid Mechanics Department, Etablissement de Lyon, 69360 Solaize, France
*
†Email address for correspondence: frigaard@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

The purely conductive state in configurations such as the Rayleigh–Bénard one is linearly stable for yield stress fluids at all Rayleigh numbers, 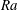$Ra$. However, on changing to localized heater configurations the static background state exists only if the yield stress is sufficiently large. Otherwise, thermal plumes may be induced in a stationary viscoplastic fluid layer, as illustrated in the recent experimental study of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). Here, we study an analogous problem both analytically and computationally, from the perspective of an ideal yield stress fluid (Bingham fluid) that is initially stationary in a locally heated rectangular tank. We show that for a non-zero yield stress the onset of flow waits for a start time 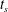$t_{s}$ that increases with the dimensionless ratio of yield stress to buoyancy stress, denoted 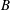$B$. We provide a precise mathematical definition of 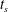$t_{s}$ and approximately evaluate this for different values of 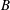$B$, using both computational and semianalytical methods. For sufficiently large 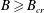$B\geqslant B_{cr}$, the fluid is unable to yield. For the flow studied, 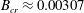$B_{cr}\approx 0.00307$. The critical value 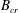$B_{cr}$ and the start time 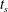$t_{s}$, for 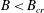$B<B_{cr}$, are wholly independent of 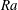$Ra$ and 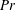$Pr$. For 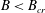$B<B_{cr}$, yielding starts at 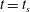$t=t_{s}$. The flow develops into either a weakly or a strongly convective flow. In the former case the passage to a steady state is relatively smooth and monotone, resulting eventually in a steady convective plume above the heater, rising and impinging on the upper wall, then recirculating steadily around the tank. With strongly convecting flows, for progressively larger 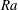$Ra$ we observe an increasing number of distinct plume heads and a tendency for plumes to develop as short-lived pulses. Over a certain range of 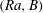$(Ra,B)$ the flow becomes temporarily frozen between two consecutive pulses. Such characteristics are distinctly reminiscent of the experimental work of Davaille et al. (J. Non-Newtonian Fluid Mech., vol. 193, 2013, 144–153). The yield stress plays a multifaceted role here as it affects plume temperature, size and velocity through different mechanisms. On the one hand, increasing 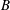$B$ tends to increase the maximum temperature of the plume heads. On the other hand, for larger 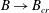$B\rightarrow B_{cr}$, the plume never starts.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 787 , 25 January 2016 , pp. 474 - 507
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J., Frigaard, I. A. & Ovarlez, G. 2014 Yielding to stress: recent developments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 46, 121–146.Google Scholar
Balmforth, N. J. & Rust, A. C. 2009 Weakly nonlinear viscoplastic convection. J. Non-Newtonian Fluid. Mech. 158 (1–3), 36–45.Google Scholar
Barnes, H. A. 1999 The yield stress – a review or ‘ ${\rm\pi}{\it\alpha}{\it\nu}{\it\tau}{\it\alpha}~{\it\rho}{\it\epsilon}{\it\iota}$ ’ – everything flows? J. Non-Newtonian Fluid. Mech. 81, 133–178.Google Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80 (345), 339–358.Google Scholar
Bayazitoglu, Y., Paslay, P. R. & Cernocky, P. 2007 Laminar Bingham fluid flow between vertical parallel plates. Intl J. Therm. Sci. 46 (4), 349–357.Google Scholar
Bonn, D., Paredes, J., Denn, M. M., Berthier, L., Divoux, T. & Manneville, S.2015 Yielding to stress: recent developments in viscoplastic fluid mechanics, Preprint submitted arXiv:1502.05281v1.Google Scholar
Cherkasov, S. G. 1979 Combined convection of a viscoplastic liquid in a plane vertical layer. Fluid Dyn. 14 (6), 901–903.Google Scholar
Coussot, P. 2014 Yield stress fluid flows: a review of experimental data. J. Non-Newtonian Fluid. Mech. 211, 31–49.Google Scholar
Darbouli, M., Metivier, C., Piau, J. M., Magnin, A. & Abdelali, A. 2013 Rayleigh–Bénard convection for viscoplastic fluids. Phys. Fluids 25 (2), 023101.Google Scholar
Davaille, A., Gueslin, B., Massmeyer, A. & Giuseppe, E. Di 2013 Thermal instabilities in a yield stress fluid: existence and morphology. J. Non-Newtonian Fluid Mech. 193, 144–153.Google Scholar
Divoux, T., Barentin, C. & Manneville, S. 2011 From stress-induced fluidization processes to Herschel–Bulkley behaviour in simple yield stress fluids. Soft Matt. 7, 8409–8418.Google Scholar
Frigaard, I. A. & Nouar, C. 2005 On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newtonian Fluid. Mech. 127 (1), 1–26.Google Scholar
Gershuni, G. Z. & Zhukhovitski, E. M. 1973 Convective stability of Bingham fluid. Dokl. Akad. Nauk SSSR 208 (1), 63–65.Google Scholar
Glowinski, R. & Wachs, A. 2011 Numerical Methods for non-Newtonian Fluids, Special Volume, Handbook of Numerical Analysis, vol. XVI, On the numerical simulation of viscoplastic fluid flow, pp. 483–718. North-Holland.CrossRefGoogle Scholar
Hassan, M. A., Pathak, M. & Khan, M. K. 2013 Natural convection of viscoplastic fluids in a square enclosure. Trans. ASME J. Heat Transfer 135 (12), 122501.Google Scholar
Huilgol, R. R. & Kefayati, G. R. 2015 Natural convection problem in a Bingham fluid using the operator–splitting method. J. Non-Newtonian Fluid. Mech. 220, 22–32.Google Scholar
Kaminski, E. & Jaupart, C. 2003 Laminar starting plumes in high-Prandtl-number fluids. J. Fluid Mech. 478, 287–298.Google Scholar
Karimfazli, I. & Frigaard, I. A. 2013 Natural convection flows of a Bingham fluid in a long vertical channel. J. Non-Newtonian Fluid. Mech. 201, 39–55.CrossRefGoogle Scholar
Karimfazli, I., Frigaard, I. A. & Wachs, A. 2015 A novel heat transfer switch using the yield stress. J. Fluid Mech. 783, 526–566.Google Scholar
Kebiche, Z., Castelain, C. & Burghelea, T. 2014 Experimental investigation of the Rayleigh–Bénard convection in a yield stress fluid. J. Non-Newtonian Fluid. Mech. 203, 9–23.Google Scholar
Lyubimova, T. P. 1977 Numerical investigation of convection in a viscoplastic liquid in a closed region. Fluid Dyn. 12 (1), 1–5.Google Scholar
Massmeyer, A., Giuseppe, E. Di, Davaille, A., Rolf, T. & Tackley, P. J. 2013 Numerical simulation of thermal plumes in a Herschel–Bulkley fluid. J. Non-Newtonian Fluid Mech. 195, 32–45.Google Scholar
Moses, E., Zocchi, G. & Libchaber, A. 1993 An experimental study of laminar plumes. J. Fluid Mech. 251, 581–601.Google Scholar
Ovarlez, G., Cohen-Addad, S., Krishan, K., Goyon, J. & Coussot, P. 2013 On the existence of a simple yield stress fluid behavior. J. Non-Newtonian Fluid Mech. 193, 68–79.Google Scholar
Patel, N. & Ingham, D. B. 1994 Analytic solutions for the mixed convection flow of non-Newtonian fluids in parallel plate ducts. Intl Commun. Heat Mass Transfer 21 (1), 75–84.Google Scholar
Prager, W.1954 On slow visco-plastic flow, in: Studies in Mathematics and Mechanics (Presented to Richard von Mises by Colleagues, Friends, and Pupils).Google Scholar
Ribe, N., Davaille, A. & Christensen, U. 2007 Mantle Plumes: A Multidisciplinary Approach, Fluid Dynamics of Mantle Plumes. Springer.Google Scholar
Sparrow, E. M., Husar, R. B. & Goldstein, R. J. 1970 Observations and other characteristics of thermals. J. Fluid Mech. 41 (04), 793–800.Google Scholar
Temam, R. & Strang, G. 1980 Functions of bounded deformation. Arch. Rat. Mech. Anal. 75 (1), 7–21.Google Scholar
Turan, O., Chakraborty, N. & Poole, R. J. 2010 Laminar natural convection of Bingham fluids in a square enclosure with differentially heated side walls. J. Non-Newtonian Fluid. Mech. 165 (15–16), 901–913.Google Scholar
Turan, O., Chakraborty, N. & Poole, R. J. 2012 Laminar Rayleigh–Bénard convection of yield stress fluids in a square enclosure. J. Non-Newtonian Fluid. Mech. 171, 83–96.Google Scholar
Turan, O., Poole, R. J. & Chakraborty, N. 2011 Aspect ratio effects in laminar natural convection of Bingham fluids in rectangular enclosures with differentially heated side walls. J. Non-Newtonian Fluid. Mech. 166 (3–4), 208–230.Google Scholar
de Vahl Davis, G. 1983 Natural convection of air in a square cavity: a bench mark numerical solution. Intl J. Numer. Meth. Fluids 3 (3), 249–264.Google Scholar
Vikhansky, A. 2009 Thermal convection of a viscoplastic liquid with high Rayleigh and Bingham numbers. Phys. Fluids 21 (10), 103103.Google Scholar
Vikhansky, A. 2010a On the onset of natural convection of Bingham liquid in rectangular enclosures. J. Non-Newtonian Fluid. Mech. 165 (23–24), 1713–1716.Google Scholar
Vikhansky, A. 2010b On the stopping of thermal convection in viscoplastic liquid. Rheol. Acta 50 (4), 423–428.Google Scholar
Wachs, A., Hammouti, A., Vinay, G. & Rahmani, M. 2015 Accuracy of finite volume/staggered grid distributed Lagrange multiplier/fictitious domain simulations of particulate flows. Comput. Fluids 115, 154–172.Google Scholar
Xue, J.2007 Thermal and rheological properties of batter systems. PhD thesis, McGill University.Google Scholar
Yang, W. J. & Yeh, H. C. 1965 Free convective flow of Bingham plastic between two vertical plates. Trans. ASME J. Heat Transfer 87 (2), 319.Google Scholar
Zhang, J., Vola, D. & Frigaard, I. A. 2006 Yield stress effects on Rayleigh–Bénard convection. J. Fluid Mech. 566, 389–419.Google Scholar