Abstract
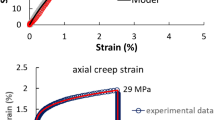
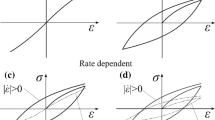
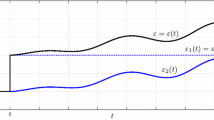
The quasi-static viscoelastic response of polymeric materialsis investigated utilizing constitutive models based on fractionalcalculus. Time-based fractional calculus analysis techniques areemphasized. Analytic solutions to quasi-static boundary value problemsin which the viscoelastic behavior is characterized by thefour-parameter fractional calculus-based solid model are given. Varioussets of data from the literature are fit with existing and newfractional calculus-based constitutive equations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bagley, R.L., ‘Power law and fractional calculus model of viscoelasticity’ AIAA Journal 27(10), 1986, 1412–1417.
Bagley, R.L. and Torvik, P.J., ‘A theoretical basis for the application of fractional calculus to viscoelasticity’ Journal of Rheology 27(3), 1983, 201–210.
Bagley, R.L. and Torvik, P.J., ‘On the fractional calculus model of viscoelastic behavior’ Journal of Rheology 30(1), 1986, 133–155.
Caputo, M. and Mainardi, F., ‘A new dissipation model based on memory mechanism’ Pure and Applied Geophysics 91, 1971, 134–147.
Christensen, R.M., Theory of Viscoelasticity, An Introduction, 2nd edn., Academic Press, New York, 1982.
Drozdov, A., Viscoelastic Structures, Academic Press, New York, 1998.
Erdelyi, A., Magnus, W., Oberheltinger, F. and Tricomi, F.G., Higher Transcendental Functions, Vol. 3, McGraw-Hill, New York, 1954, 206–209.
Friedrich, C., ‘Rheological material functions for associating comb-shaped or H-shaped polymers’ Philosophical Magazine Letters 66(6), 1992, 287–292.
Gottenberg, W.G. and Christensen, R.M., ‘An experiment for determination of the mechanical property in shear for a linear, isotropic viscoelastic solid’ International Journal of Engineering Science 2, 1964, 45–57.
Koeller, R.C., ‘Applications of fractional calculus to the theory of viscoelasticity’ Journal of Applied Mechanics 51, 1984, 299–307.
Koeller, R.C., ‘Polynomial operator, Stieltjes convolution and fractional calculus in hereditary mechanics’ Acta Mechanica 58, 1986, 251–264.
Padovan, J., ‘Computational algorithms for FE formulations involving fractional operators’ Computational Mechanics 2, 1987, 271–287.
Tobolsky, A.V., Properties and Structure of Polymers, Wiley, New York, 1960.
Tobolsky, A.V. and Catsiff, E., ‘Elastoviscous properties of polyisobutylene (and other amorphous polymers) from stress-relaxation studies. IX. A summary of results’ International Journal of Engineering Science 2, 1964, 111–121.
Tschoegl, N.W., The Phenomenological Theory of Linear Viscoelastic Behavior, Springer-Verlag, Berlin, 1989.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Welch, S.w., Rorrer, R.A. & Duren, R.G. Application of Time-Based Fractional Calculus Methods to Viscoelastic Creep and Stress Relaxation of Materials. Mechanics of Time-Dependent Materials 3, 279–303 (1999). https://doi.org/10.1023/A:1009834317545
Issue Date:
DOI: https://doi.org/10.1023/A:1009834317545