Abstract
Fractional time derivatives are used to deduce a generalization ofviscoelastic constitutive equations of differential operator type. Theseso-called fractional constitutive equations result in improvedcurve-fitting properties, especially when experimental data from longtime intervals or spanning several frequency decades need to be fitted.Compared to integer-order time derivative concepts less parameters arerequired. In addition, fractional constitutive equations lead to causalbehavior and the concept of fractional derivatives can be physicallyjustified providing a foundation of fractional constitutive equations.
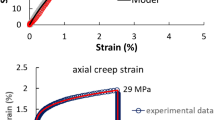
First, three-dimensional fractional constitutive equations based onthe Grünwaldian formulation are derived and their implementationinto an elastic FE code is demonstrated. Then, parameter identificationsfor the fractional 3-parameter model in the time domain as well as inthe frequency domain are carried out and compared to integer-orderderivative constitutive equations. As a result the improved performanceof fractional constitutive equations becomes obvious. Finally, theidentified material model is used to perform an FE time steppinganalysis of a viscoelastic structure.
Similar content being viewed by others
References
Abel, N., 'Solution de quelques problèmes à l'aide d'intégrales définites', Christiania Grondahl, Norway, 1881, pp. 16–18.
Bagley, R. L., 'Power law and fractional calculus model of viscoelasticity', AIAA Journal 27(10), 1989, 1412–1417.
Bagley, R. L. and Torvik, P. J., 'A theoretical basis for the application of fractional calculus to viscoelasticity', Journal of Rheology 27(3), 1983, 201–210.
Bagley, R. L. and Torvik, P. J., 'On the fractional calculus model of viscoelastic behaviour', Journal of Rheology 30(1), 1986, 133–155.
Caputo, M., 'Vibrations on an infinite viscoelastic layer with a dissipative memory', Journal of the Acoustical Society of America 56(3), 1974, 897–904.
Caputo, M. and Mainardi, F., 'A new dissipation model based on memory mechanism', Pure and Applied Geophysics 91, 1971, 134–147.
Cupial, P., 'Some approaches to the analyses of nonproportionally damped viscoelastic structures', in Proceedings of Dynamics of Continua, Bad Honnef, Germany, September 9–13, D. Besdo and R. Bogacz (eds.), Shaker-Verlag, 1996, pp. 93–102.
Enelund, M. and Josefson, B. M., 'Time-domain Finite Element analysis of viscoelastic structures with fractional derivatives constitutive relations', AIAA Journal 35(10), 1997, 1630–1637.
Enelund M., Mähler, L., Runesson, B., and Josefson, B. M., 'Formulation and integration of the standard linear viscoelastic solid with fractional order rate laws', Journal of Solids and Structures 36, 1999, 2417–2442.
Gaul, L., 'The influence of damping on waves and vibrations', Mechanical Systems and Signal Processing 13(1), 1999, 1–30.
Gaul, L. and Schanz, M., 'A comparative study of three boundary element approaches to calculate the transient response of viscoelastic solids with unbounded domains', Computer Methods in Applied Mechanics and Engineering 179, 1999, 111–123.
Gemant, A., 'A method of analyzing experimental results obtained from elasto-viscous bodies', Physics 7, 1936, 311–317.
Gemant, A., 'On fractional differentials', The Philosophical Magazine 25, 1938, 540–549.
Grünwald, A. K., 'Ñber 'begrenzte' Derivationen und deren Anwendung', Zeitschrift für angewandte Mathematik und Physik 12, 1867, 441–480.
Koeller, R. C., 'Applications of fractional calculus to the theory of viscoelasticity', ASME Journal of Applied Mechanics 51, 1984, 299–307.
Lacroix, S., Traité du calcul differentiel et du calcul intégral, Courcier, Paris, 1819.
Leibniz, G., Leibnizsche Mathematische Schriften, Georg Olm Verlag, Hildesheim, 1962.
Liouville, J., 'Mémoire sur le calcul des différentielles à indices quelconques', Journal d'Ecole Polytechnique 13, 1832, 71–162.
Liouville, J., 'Mémoire sur quelques quéstions de géomerie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces quéstions', Journal d'Ecole Polytechnique 13, 1832, 1–69.
Liouville, J., 'Mémoire sur le théoreme des fonctions complémentaires', Journal für die reine und angewandte Mathematik 11, 1834, 1–19.
Nutting, P. G., 'A new general law of deformation', Journal of the Franklin Institute 191, 1921, 679–685.
Oldham, K. B. and Spanier, J., The Fractional Calculus, Academic Press, New York, 1974.
Padovan, J., 'Computational algorithms for FE formulations involving fractional operators', Computational Mechanics 2, 1987, 271–287.
Podlubny, I., Fractional Differential Equations, Academic Press, San Diego, CA, 1999.
Ross, B., 'A brief history and exposition of the fundamental theory of fractional calculus', Fractional Calculus and Its Applications, Lecture Notes in Mathematics, Vol. 457, Springer-Verlag, Berlin, 1975.
Rossikhin, Y. A. and Shitikova, M. V., 'Application of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids', Applied Mechanics Reviews 50(1), 1997, 15–67.
Scott Blair, G. W. and Caffyn, J. E., 'An application of the theory of quasi-properties to the treatment of anomalous strain-stress relations', The Philosophical Magazine 40, 1949, 80–94.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Schmidt, A., Gaul, L. Finite Element Formulation of Viscoelastic Constitutive Equations Using Fractional Time Derivatives. Nonlinear Dynamics 29, 37–55 (2002). https://doi.org/10.1023/A:1016552503411
Issue Date:
DOI: https://doi.org/10.1023/A:1016552503411