Skip to main content
SpringerLink
Log in

Analysis of the dynamic responses for a pre-cracked three-point bend specimen

  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

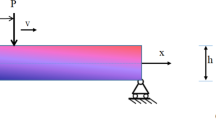
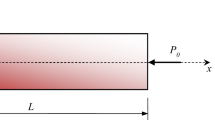
In this paper, shear deformation and rotary inertia was introduced into the calculation of the dynamic stress intensity factor by means of solving the stiffness of a pre-cracked three-point bend specimen. A simple formula of dynamic stress intensity factor for a pre-cracked three-point bend specimen is derived using the vibration analysis method. Dynamic three-point bending tests were performed on a uniquely modified Hopkinson pressure bar, allowing the dynamic responses of the pre-cracked specimen, such as: the natural frequency, the period of apparent specimen oscillations, the dynamic loads, and the dynamic stress intensity factor to be analyzed experimentally and theoretically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • ASTM Standard E399-90. (2002). 'Standard test method for plane strain fracture toughness of metallic materials', Annual Book of ASTM Standards, ASTM International. Baltimore pp. 443-473.

  • Bacon, C., Farm, J. and Lataillade, J.L. (1994). Dynamic fracture toughness determined from load-point displacement. Experimental Mechanics 34, 217–222.

    Article  Google Scholar 

  • Böhme, A.W. and Kalthoff, J.F. (1982). The behaviour of notched bend specimens in impact testing. International Journal of Fracture, 20, R139–R143.

    Article  Google Scholar 

  • Boyer, H.E. and Gall, T.L. (1985). Metals Handbook. 9Th Ed., American Society for Metals, Ohio pp. 190–207.

    Google Scholar 

  • Bucci, R.J., Paris, P.C., Landes, J.D. and Rice, J.R. (1972). J integral estimation procedures. In: H.T. Corten (ed.) Fracture Toughness. ASTM STP514, Part II. Philadelphia pp. 40–69.

  • Costin, L.S., Duffy, J. and Freund, L.B. (1977). Fracture initiation in metals under stress wave loading conditions. Fast fracture and crack arrest, ASTM STP627, American Science for Testing Materials, Philadelphia, PA. 1977, 301–318.

  • Cowper, G.R. (1966). The shear coefficient in Timoshenko's beams theory. Journal of Applied Mechanics 3, 335–340.

    Google Scholar 

  • Dally, J.W. and Sanford, R.J. (1987). Strain-gage methods for measuring the opening-mode stress-intensity factor, K IC . Experimental Mechanics 27, 381–388.

    Article  Google Scholar 

  • Dally, J.W. and Barker, D.B. (1988). Dynamic measurements of initiation toughness at high loading rates. Experimental Mechanics 28, 298–303.

    Article  Google Scholar 

  • Dutton, A.G. and Mines, R.A.W. (1991). Analysis of the Hopkinson pressure bar loaded instrumented Charpy test using an inertial modeling technique. International Journal of Fracture 51, 87–206.

    Google Scholar 

  • Freund, L.B. (ed.) (1990). Dynamic Fracture Mechanics. Cambridge University Press pp. 74.

  • Giovanola, J.H. (1986). Investigation and application of the one-point-bend impact test. Fracture mechanics: ASTM STP 905, (Edited by J.H. Underwood, R. Chait, C.W. Smith, D.P. Wilhem, W.A. Andres and J.C. Newman), American Society for Testing and Materials, Philadelphia, 307–328.

  • Gopalaratnam, V.S., Shah, S.P. and John, R. (1984). A modified instrumented Charpy test for cement-based composites. Experimental Mechanics 6, 102–111.

    Google Scholar 

  • Guo, W.G., Li, Y.L. and Liu, Y.Y. (1997). Analytical and experimental determination of dynamic impact stress intensity factor for 40Cr steel. Theoretical and Applied Fracture Mechanics 26, 29–34.

    Article  Google Scholar 

  • Ireland, D.R. (1975). 'Comments on EPRI Instrumented impact Procedures', Technical Report TR 75-37, EPRI Fracture Toughness Program Information Meeting, May 1975, Effects Technology, Inc.

  • Kalthoff, J.F. (1985). On the measurement of dynamic fracture toughness-A review of recent work. International Journal of Fracture 27, 277–298.

    Article  Google Scholar 

  • Kalthoff, J.F. (1986). Fracture behavior under high rates of loading. Engineering Fracture Mechanics 23, 289–298.

    Article  Google Scholar 

  • Kishimoto, K., Aoki, S. and Sakata, M. (1980). Simple formula for dynamic stress intensity factor of pre-cracked Charpy specimen. Engineering Fracture Mechanics 13, 501–508.

    Google Scholar 

  • Kishimoto, K., Kuroda, M., Aoki, S. and Sakata, M. (1984) Simple formulas for dynamic fracture mechanics parameters of elastic and viscoelastic three-point bend specimen based on Timoshenko's beam theory. In: S.R Valluri, D.M.R. Taplin et al (eds.) Advances in Fracture Research pp. 3177–3184.

  • Klepaczko, J.R. (1982). Discussion of a new experimental method in measuring fracture initiation at high loading rates by stress waves. ASME Journal of Engineering Materials and Technology 104, 29–35.

    Google Scholar 

  • Kobayashi, T., Yamamoto, I. and Ninomi, M. 1986). Evaluation of dynamic fracture toughness parameters by instrumented Charpy impact test. Engineering Fracture Mechanics 24, 773–782.

    Google Scholar 

  • Macke, Th., Martin, E., Balette, J.J. and Quenisset, J.M. (1990). Compliance calibration during instrumented Charpy impact testing. Engineering Fracture Mechanics 37, 831–838.

    Article  Google Scholar 

  • Marur, P.R., Simha, K.R.Y. and Nair, P.S. (1994). Dynamic analysis of three-point bend specimen under impact. International Journal of Fracture 68, 261–273.

    Article  Google Scholar 

  • Marur, P.R. (1995). The inertial effect in Charpy impact test. Engineering Fracture Mechanics 52, 1165–1166.

    Article  Google Scholar 

  • Marur, P.R. (1996a). On the effects of higher vibration modes in the analysis of three-point bend testing. International Journal of Fracture 77, 367–379.

    Article  Google Scholar 

  • Marur, P.R. (1996b). Numerical simulation of anvil interactions in the impact testing of notched bend specimens. International Journal of Fracture 81, 27–37.

    Article  Google Scholar 

  • Marur, P.R., Nair, P.S. and Simha, K.R.Y. (1996c). Two degrees of freedom modeling of pre-cracked beams under impact. Engineering Fracture Mechanics 53, 481–491.

    Article  Google Scholar 

  • Marur, P.R. (1998). Charpy specimen-A simply supported beam or a constrained free-free beam. Engineering Fracture Mechanics 61, 369–386.

    Article  Google Scholar 

  • Marur, P.R. (2000). Dynamic analysis of one-point impact test. Engineering Fracture Mechanics 67, 41–53.

    Article  Google Scholar 

  • Nash, G.E. (1969). An analysis of the forces and bending moments generated during the notched impact test. International Journal of Fracture Mechanics 5, 269–286.

    Article  Google Scholar 

  • Orynyak, I.V. and Krasowsky, A.J. (1998). The modeling of elastic response of a three-point bend specimen under impact loading. Engineering Fracture Mechanics 60, 563–575.

    Article  Google Scholar 

  • Rizal, S. and Homma, H. (2000). Dimple fracture under short pulse loading. International Journal of Impact Engineering 24, 69–83.

    Article  Google Scholar 

  • Rokach, I.V. 1998). Modal approach for processing one-and three-point bend test data for DSIF-time diagram determination. Part I-theory, Part II-calculations and results. Fatigue & Fracture of Engineering Materials & Structure 21, 1007–1026.

    Google Scholar 

  • Ruiz, C. and Mines, R.A.W. (1985). The Hopkinson pressure bar: An alternative to the instrumented pendulum for Charpy tests. International Journal of Fracture 29, 101–109.

    Google Scholar 

  • Sahraou, S. and Latallade, J.L. (1998). Analysis of load oscillations in instrumented impact testing. Engineering Fracture Mechanics 60, 437–446.

    Google Scholar 

  • Server, W.L., Wullaert, R.A. and Sheckherd, J.W. (1977). Evaluation of current procedures for dynamic fracture-toughness testing. In: Jane B. Wheeler (ed.) Flaw Growth and Fracture. ASTM STP 631. Philadelphia pp. 446–461.

  • Srawley, J.E. (1976). Wide range stress intensity factor expressions for ASTM E399 standard fracture toughness specimens. International Journal of Fracture 12, 475–476.

    Google Scholar 

  • Tada, H., Paris, P.C. and Irwin, G.R. (2000). The Stress Analysis of Cracks Handbook, Third Edition. ASME Press, New York pp. 58–60.

    Google Scholar 

  • Yokoyama, T. (1993). Determination of dynamic fracture-initiation toughness using a novel impact bend test procedure. Journal of Pressure Vessel Technology 115, 389–397.

    Google Scholar 

  • Wada, H., Seika, M. et al. (1993). Measurement of impact fracture toughness for PMMA with single-point bending test using an air gun. Engineering Fracture Mechanics 46, 715–719.

    Article  Google Scholar 

  • Weisbrod, G. and Rittel, D. (2000). A method for dynamic fracture toughness determination using short beams. International Journal of Fracture 104, 89–103.

    Article  Google Scholar 

  • Williams, J.G. (1987). The analysis of dynamic fracture using lumped mass-spring modes. International Journal of Fracture 33, 47–59.

    ADS  Google Scholar 

  • Williams, J.G., Tropsa, V. et al. (2001). Dynamic correction factors for K and G in high rate, SENB, impact tests. International Journal of Fracture 107, 259–278.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, University of California-San Diego, La Jolla, CA, 92093-0411

    Fengchun Jiang, Aashish Rohatgi, Kenneth S. Vecchio & Justin L. Cheney

Authors
  1. Fengchun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aashish Rohatgi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kenneth S. Vecchio
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Justin L. Cheney
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jiang, F., Rohatgi, A., Vecchio, K.S. et al. Analysis of the dynamic responses for a pre-cracked three-point bend specimen. International Journal of Fracture 127, 147–165 (2004). https://doi.org/10.1023/B:FRAC.0000035058.03627.30

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:FRAC.0000035058.03627.30

Search

Navigation