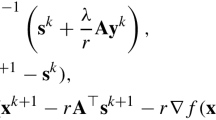Skip to main content
SpringerLink
Log in

Pseudomonotone Variational Inequalities: Convergence of the Auxiliary Problem Method

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

This paper deals with the convergence of the algorithm built on the auxiliary problem principle for solving pseudomonotone (in the sense of Karamardian) variational inequalities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Harker, P. T., and Pang, J. S., Finite-Dimensional Variational Inequality and Nonlinear Complementarity Problems: A Survey of Theory, Algorithms, and Applications, Mathematical Programming, Vol. 48, pp. 161–220, 1990.

    Google Scholar 

  2. Karamardian, S., Complementarity Problems over Cones with Monotone and Pseudomonotone Maps, Journal of Optimization Theory and Applications, Vol. 18, pp. 445–455, 1976.

    Google Scholar 

  3. Karamardian, S., and Schaible, S., Seven Kinds of Monotone Maps, Journal of Optimization Theory and Applications, Vol. 66, pp. 37–47, 1990.

    Google Scholar 

  4. Schaible, S., Generalized Monotonicity: A Survey, Generalized Convexity, Edited by S. Komlosi, R. Rapcsak, and S. Schaible, Springer Verlag, Heidelberg, Germany, pp. 229–249, 1994.

    Google Scholar 

  5. Karamardian, S., Schaible, S., and Crouzeix, J. P., Characterizations of Generalized Monotone Maps, Journal of Optimization Theory and Applications, Vol. 76, pp. 399–413, 1993.

    Google Scholar 

  6. Komlosi, S., Generalized Monotonicity and Generalized Convexity, Journal of Optimization Theory and Applications, Vol. 84, pp. 361–376, 1995.

    Google Scholar 

  7. Zhu, D., and Marcotte, P., New Classes of Generalized Monotonicity, Journal of Optimization Theory and Applications, Vol. 87, pp. 457–471, 1995.

    Google Scholar 

  8. Mangasarian, O. L., Pseudoconvex Functions, SIAM Journal on Control, Vol. 3, pp. 281–290, 1965.

    Google Scholar 

  9. Mangasarian, O. L., Nonlinear Programming, SIAM, Philadelphia, Pennsylvania, 1994.

    Google Scholar 

  10. Schaible, S., Generalized Monotonicity: Concepts and Uses, Variational Inequalities and Network Equilibrium Problems, Edited by F. Giannessi and A. Maugeri, Plenum Publishing Corporation, New York, NY, pp. 289–299, 1995.

    Google Scholar 

  11. Yao, J. C., Variational Inequalities with Generalized Monotone Operators, Mathematics of Operations Research, Vol. 19, pp. 691–705, 1994.

    Google Scholar 

  12. Yao, J. C., Multivalued Variational Inequalities with K-Pseudomonotone Operators, Journal of Optimization Theory and Applications, Vol. 83, pp. 391–403, 1994.

    Google Scholar 

  13. Crouzeix, J. P., Pseudomonotone Variational Inequality Problems: Existence of Solutions, Mathematical Programming, Vol. 78, pp. 305–314, 1997.

    Google Scholar 

  14. Zhu, D. L., and Marcotte, P., Cocoercivity and Its Role in the Convergence of Iterative Schemes for Solving Variational Inequalities, SIAM Journal on Optimization, Vol. 6, pp. 714–726, 1996.

    Google Scholar 

  15. Eckstein, J., and Bertsekas, D. P., On the Douglas–Rachford Splitting Method and the Proximal Point Algorithm for Maximal Monotone Operators, Mathematical Programming, Vol. 55, pp. 293–318, 1992.

    Google Scholar 

  16. Mataoui, M. A., Contributions à la Décomposition et à l' Agrégation des Problèmes Variationnels, Thesis Dissertation, É cole des Mines de Paris, Fontainebleau, France, 1990.

    Google Scholar 

  17. Brezis, H., Equations et Inéquations Nonlinéaires dans les Espaces Vectoriels en Dualité, Annales de l'Institut Fourier, Vol. 18, pp. 115–175, 1968.

    Google Scholar 

  18. Cohen, G., Optimization by Decomposition and Coordination: A Unified Approach, IEEE Transactions on Automatic Control, Vol. 23, pp. 222–232, 1978.

    Google Scholar 

  19. Cohen, G., Auxiliary Problem Principle and Decomposition of Optimization Problems, Journal of Optimization Theory and Applications, Vol. 32, pp. 277– 305, 1980.

  20. Cohen, G., and Zhu, D. L., Decomposition-Coordination Methods in Large Scale Optimization Problems: The Nondifferentiable Case and the Use of Augmented Lagrangians, Advances in Large Scale Systems Theory and Applications, Edited by J. B. Cruz, JAI Press, Greenwich, Connecticut, Vol. 1, pp. 203–266, 1983.

    Google Scholar 

  21. Cohen, G., Auxiliary Problem Principle Extended to Variational Inequalities, Journal of Optimization Theory and Applications, Vol. 59, pp. 325–333, 1988.

    Google Scholar 

  22. Bregman, L. M., The Relaxation Method of Finding the Common Point of Convex Sets and Its Applications to the Solution of Problems in Convex Programming, USSR Computational Mathematics and Mathematical Physics, Vol. 7, pp. 200–217, 1967.

    Google Scholar 

  23. Eckstein, J., Nonlinear Proximal Point Algorithms Using Bregman Functions, Mathematics of Operations Research, Vol. 18, pp. 202–226, 1993.

    Google Scholar 

  24. Pang, J. S., and Chan, D., Iterative Methods for Variational and Complementarity Problems, Mathematical Programming, Vol. 24, pp. 284–313, 1982.

    Google Scholar 

  25. El Farouq, N., and Cohen, G., Progressive Regularization of Variational Inequalities and Decomposition Algorithms, Journal of Optimization Theory and Applications, Vol. 97, pp. 407–433, 1998.

    Google Scholar 

  26. Cohen, G., and Chaplais, F., Nested Monotony for Variational Inequalities over Product of Spaces and Convergence of Iterative Algorithms, Journal of Optimization Theory and Applications, Vol. 59, pp. 369–390, 1988.

    Google Scholar 

  27. El Farouq, N., and Cohen, G., Convergence of a Zero-Finding Algorithm for Some Nonmonotone Linear Operators, Preprint, É cole des Mines, Paris, France, 1998.

    Google Scholar 

  28. Auslender, A., Optimization, Méthodes Numériques, Masson, Paris, France, 1976.

    Google Scholar 

  29. Arrow, K. J., and Enthoven, A. C., Quasiconcave Programming, Econometria, Vol. 29, pp. 779–800, 1961.

    Google Scholar 

  30. El Farouq, N., Pseudoconvex Optimization Problems: Convergence of the Auxiliary Problem Method, Report 00178, LAAS CNRS, Toulouse, France, 2000.

    Google Scholar 

  31. El Farouq, N., A Convergent Algorithm Based on the Progressive Regularization for Solving Pseudomonotone Variational Inequalities, Preprint, LAAS CNRS, Toulouse, France, 2000.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Université Blaise Pascal, Clermont II and LAAS CNRS, Toulouse, France

    N. El Farouq (Maître de Conférences)

Authors
  1. N. El Farouq
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

El Farouq, N. Pseudomonotone Variational Inequalities: Convergence of the Auxiliary Problem Method. Journal of Optimization Theory and Applications 111, 305–322 (2001). https://doi.org/10.1023/A:1012234817482

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1012234817482

Search

Navigation