Abstract
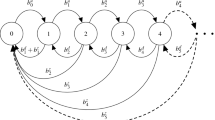
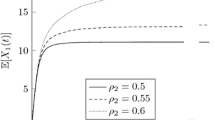
In this paper, we present a novel approach to determining the steady-state distribution for the number of jobs present in a 2-class, single server preemptive priority queueing model where the low priority source population is finite. Arrivals are assumed to be Poisson with exponential service times. The system investigated is a quasi birth and death process, and the joint distribution is derived via the method of generalized eigenvalues. Using this approach, we are able to obtain all eigenvalues and corresponding eigenvectors explicitly. Furthermore, we link this method to the matrix analytic approach by obtaining an explicit solution for the rate matrix R. Two numerical examples are given to illustrate the procedure and highlight some important computational features.
Similar content being viewed by others
References
A.S. Alfa, Matrix-geometric solution of discrete time MAP/PH/1 priority queue, Naval Research Logistics 45 (1998) 23-50.
D. Bertsimas, An analytic approach to a general class of G/G/s queueing systems, Operations Research 38 (1990) 139-155.
W.S. Dorn and D.D. McCracken, NumericalMethods with Fortran IV Case Studies (Wiley, New York, 1972).
H.R. Gail, S.L. Hantler and B.A. Taylor, Analysis of a non-preemptive priority multiserver queue, Advances in Applied Probability 20 (1988) 852-879.
E. Gelenbe and I. Mitrani, Analysis and Synthesis of Computer Systems (Academic Press, London, 1980).
P. Gohberg, P. Lancaster and L. Rodman, Matrix Polynomials (Academic Press, New York, 1982).
W.K. Grassmann and S. Drekic, An analytical solution for a tandem queue with blocking, Queueing Systems 36 (2000) 221-235.
W.K. Grassmann and J. Tavakoli, A tandem queue with movable servers: an eigenvalue approach, Preprint (2001).
B.R. Haverkort and A. Ost, Steady-state analysis of infinite stochastic Petri nets: A comparison between the spectral expansion and the matrix-geometric method, in: Proc. of 7th International Workshop on Petri Nets and Performance Models, Saint Malo, France (IEEE Computer Society Press, Silver Spring, Maryland, 1997) pp. 36-45.
E.P.C. Kao and K.S. Narayanan, Computing steady-state probabilities of a non-preemptive priority multiserver queue, ORSA Journal of Computing 2 (1990) 211-218.
L. Kleinrock, Queueing Systems, Volume II: Computer Applications (Academic Press, London, 1980).
G. Latouche and V. Ramaswami, A logarithmic reduction algorithm for quasi-birth-death processes, Journal of Applied Probability 30 (1993) 650-674.
D.R. Miller, Computation of steady-state probabilities for M/M/1 priority queues, Operations Reserach 29 (1981) 945-958.
I. Mitrani and R. Chakka, Spectral expansion solution for a class of Markov models: Application and comparison with the matrix-geometric method, Performance Evaluation 23 (1995) 241-260.
P.M. Morse, Queues, Inventories and Maintenance (Wiley, New York, 1958).
M.F. Neuts, The probabilistic significance of the rate matrix in matrix-geometric invariant vectors, Journal of Applied Probability 17 (1980) 291-296.
M.F. Neuts, Matrix Geometric Solutions in Stochastic Models-An Algorithmic Approach (Dover, New York, 1981).
W.P. Pierskalla and D.J. Brailer, Applications of operations research in health care delivery, in: Operations Research and the Public Sector, eds. S.M. Pollack, M.H. Rothkopf and A. Barnett (North-Holland, Amsterdam, 1994) pp. 469-505.
B.W. Stuck and E. Arthurs, A Computer and Communications Network Performance Analysis Primer (Prentice-Hall, Englewood Cliffs, NJ, 1985).
H. Takagi, Queueing Analysis: A Foundation of Performance Evaluation, Volume 1: Vacation and Priority Systems, Part 1 (North-Holland, Amsterdam, 1991).
H. Takagi, Queueing Analysis: A Foundation of Performance Evaluation, Volume 2: Finite Systems (North-Holland, Amsterdam, 1993).
T. Takine, A nonpreemptive priority MAP/G/1 queue with two classes of customers, Journal of Operations Research Society of Japan 39 (1996) 266-290.
K. Wuyts and R.K. Boel, Efficient matrix-geometric methods for B_ISDN by using spectral decomposition of the rate matrix, in: Advances in Matrix Analytical Methods for Stochastic Models (Notable Publications, Neshanic Station, NJ, 1998) pp. 341-359.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Drekic, S., Grassmann, W.K. An Eigenvalue Approach to Analyzing a Finite Source Priority Queueing Model. Annals of Operations Research 112, 139–152 (2002). https://doi.org/10.1023/A:1020933122382
Issue Date:
DOI: https://doi.org/10.1023/A:1020933122382