Abstract
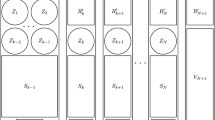
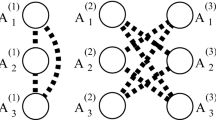
Let TT k denote the transitive tournament on k vertices. Let TT(h,k) denote the graph obtained from TT k by replacing each vertex with an independent set of size h≥1. The following result is proved: Let c 2=1/2, c 3=5/6 and c k =1−2−k−log k for k≥4. For every ∈>0 there exists N=N(∈,h,k) such that for every undirected graph G with n>N vertices and with δ(G)≥c k n, every orientation of G contains vertex disjoint copies of TT(h,k) that cover all but at most ∈n vertices. In the cases k=2 and k=3 the result is asymptotically tight. For k≥4, c k cannot be improved to less than 1−2−0.5k(1+o(1)).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alon, N. and Yuster, R.: The number of orientations having no fixed tournament, submitted.
Alon, N. and Yuster, R.: H-factors in dense graphs, J. Combin. Theory Ser. B 66 (1996), 269–282.
Bollobás, B.: Extremal Graph Theory, Academic Press, London, 1978.
Caro, Y.: Decomposition of large combinatorial structures, Arch. Math. 52 (1989), 289–297.
Chen, G., Lu X. and West, D. B.: Star-factors of tournaments, J. Graph Theory 28 (1998), 141–145.
Erdős, P. and Moser, L.: On the representation of directed graphs as unions of orderings, Publ. Math. Inst. Hungar. Acad. Sci. 9 (1964), 125–132.
Hajnal, A. and Szemerédi, E.: Proof of a conjecture of Erdős, In: P. Erdős, A. Renyi and V. T. Sós (eds), Combinatorial Theory and its Applications, Vol. II, Colloq. Math. Soc. Janos Bolyai 4, North Holland, Amsterdam, 1970, pp. 601–623.
Komlós, J.: Tiling Turán theorems, Combinatorica 20 (2000), 203–218.
Komlós, J., Sárközi, G. and Szemerédi, E.: Proof of the Alon#x2013;Yuster conjecture, Discrete Math. 235 (2001), 255–269.
Komlós, J. and Simonovits, M.: Szemerédi regularity lemma and its applications in graph theory, In: Paul Erdős is 80, Proc. Coll. Bolyai Math. Soc., Vol. 2, Keszthely, 1993, pp. 295–352.
Lonc, Z. and Truszcyński, M.: Decomposition of large uniform hypergraphs, Order 1 (1985), 345–350.
Reid, K. B.: Three problems on tournaments, In: Graph Theory and its Applications: East and West (Proc. 2nd China#x2013;USA Intl. Conf. Graph Th., San Francisco, 1989), New York Acad. Sci. Annals 576 (1989), 466–473.
Reid, K. B., and Parker, E. T.: Disproof of a conjecture of Erd?os and Moser on tournaments, J. Combin. Theory 9 (1970), 225–238.
Sanchez-Flores, A.: On tournaments free of large transitive subtournaments, Graphs Combin. 14 (1998), 181–200.
Shokoufandeh, A. and Zhao, Y.: Proof of a tiling conjecture of Komlós, Random Structures Algorithms, to appear.
Szemerédi, E.: Regular partitions of graphs, In: Proc. Colloque Inter. CNRS 260, CNRS, Paris, 1978, pp. 399–401.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Yuster, R. Tiling Transitive Tournaments and Their Blow-ups. Order 20, 121–133 (2003). https://doi.org/10.1023/B:ORDE.0000009250.31770.34
Issue Date:
DOI: https://doi.org/10.1023/B:ORDE.0000009250.31770.34