Abstract
Casson nanofluid, unsteady flow over an isothermal vertical plate with Newtonian heating (NH) is investigated. Sodium alginate (base fluid)is taken as counter example of Casson fluid. MHD and porosity effects are considered. Effects of thermal radiation along with heat generation are examined. Sodium alginate with Silver, Titanium oxide, Copper and Aluminum oxide are added as nano particles. Initial value problem with physical boundary condition is solved by using Laplace transform method. Exact results are obtained for temperature and velocity fields. Skin-friction and Nusselt number are calculated. The obtained results are analyzed graphically for emerging flow parameters and discussed. It is bring into being that temperature and velocity profile are decreasing with increasing nano particles volume fraction.
Similar content being viewed by others
Introduction
The fluid is a particular kind of matter which have no fixed shape and deforms easily due to external pressure1. Fluids are mainly of two type’s i.e Newtonian and non-Newtonian. Non-Newtonian fluids have numerous industrial applications2,3. Furthermore, its application with magnetohydrodynamic (MHD) flow in a porous medium can widely be seen in irrigation problem, biological system, petroleum, textile, polymer industries. More investigations have been published on numerous aspects of MHD non-Newtonian fluid passes over a porous medium4,5,6,7. The entropy analysis for nanofluid with different type of nano particles and water type base fluid for unsteady MHD flow was studied by8. The impact of magnetic field on free convection of nanofluid in a porous medium is presented by9. The effects of heat transfer on MHD nanofluid in a porous semi annulus has investigated by10 using numerical methods. Sheikholeslami et al.11 examined the influence of free convection in a semi annulus enclosure for ferrofluid flow in the presence of magnetic source with the consideration of thermal radiation. The observation of non-uniform magnetic field and variable magnetic field on forced convection heat is investigated by12,13. The observation of MHD on fluid flow with heat transfer is studded by14,15,16. Recently17,18 investigated the nanofluid transportation in a in the presence of magnetic source and porous cavity using CuO nano particles. The influence of external magnetic field for nanofluid as water is a base fluid of free convection flow is studied in19. Sheikholeslami and Ganji20 have investigated the effect of convective heat transfer for the nanofluid by semi analytical and numerical approaches. The same author has also investigated the influence of heat transfer for nanofluid between parallel plates in21. The influence of Lorentz forces and convection nanofluid flow is investigated by22,23,24. Dissimilar types of nano particles with water based fluid are studied by25,26. The influence of melting heat for nanofluid is studied by27. The transportation of nanofluid in porous media is investigated by28. The influence of magnetic field for nanofluid with entropy generation is analysed by29,30,31.
Nanotechnology is that kind of technology which provides the materials with size less than \(100\) nm called nanomaterials. On the basis of the structure and their properties, nanomaterials are divided into four categories32. Carbon based nano materials, metal based nano materials, Dendrimers and composite. The terminology of nanofluid was first investigated by Choi33. He defined that the fluids occupying the sizes of particles less than 100 nm is called nanofluid. The categorieswith different attitude of nano particles are particle material, Base fluid, size and concentration, of the nanofluid. Suspend these nano particles into any type of conventional fluid like oil, water, ethylene glycol to make nanofluids. The reason why nano size particles are preferred over micro size particles has been explained by34. Nano particles over micro particles, good improvement have seen in thermo physical properties. Nanofluids have various applications such as in air conditioning cooling, automotive, power plant cooling, improving diesel generator efficiency etc.35. Usually water, ethylene glycol are utilized as heat transfer base fluids. Different substances are used for the production of nanoparticles, which are generally divided into metallic i.e. copper36, metal-oxide i.e. CuO37, chalcogenides sulphides, selenides and telluride’s, mentioned38 and different particles, such like carbon nanotubes39. In literature the size of one particle is in between 20 nm40 and 100 nm41.
Casson fluid model was first presented by Casson in 1959. Casson fluids in tubes was first studied by Oka42. Examples of Casson fluids are honey, blood, soup, jelly, stuffs, slurries, artificial fibers etc. Cassonnanofluid flow with Newtonian heatingpresented by43. Sarojamma et al.44 investigated Casson nanofluid past over perpendicular cylinder in the occurrence of a transverse magnetic field with internal heat generation or absorption.
Khalid et al.45 examined unsteady MHD Casson fluid withfree convection flow in a porous medium. Bhattacharyya et al.46 studied systematically magnetohydrodynamic Casson fluid flow over a stretching shrinking sheet with wall mass transfer. Arthur et al.47 studied Casson fluid flow in excess of a perpendicular porous surface, chemical reaction in the existence of magnetic field. Recently, Fetecau et al.48 has investigated fractional nanofluids for natural convection flow over an isothermal perpendicular plate with thermal radiation. Hussanan et al.49 investigates the unsteady heat transfer flow of a non-Newtonian Casson fluid over an oscillating perpendicular plate with Newtonian heating. Recently, Imran et al.50 analyzed the effect of Newtonian heating with slip condition on MHD flow of Casson fluid. MHD flow of Casson fluid with heat transfer and Newtonian heating is analyzed by Hussanan et al.51. The effect of Newtonian heating for nanofluid is recently investigated by43,52. But no work is done until now on heat transfer enhancement in Sodium alginate fluid with additional effects of NH, MHD, porosity, heat generation, and thermal radiation. Silver (Ag), Titanium oxide (TiO2), Copper (Cu) and Aluminum oxide (Al2O3) are nano particles suspended in base fluid. Problem is solved and interpreted graphically with some conclusions.
Mathematical Modeling and solution of the Problem
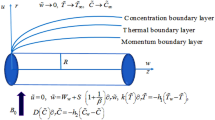
Sodium alginate with Silver (Ag), Titanium oxide (TiO2), Copper (Cu) and Aluminum oxide (Al2O3) nano particles is considered. Heat transfer, thermal radiation and heat generation are taken. Unsteady flow is over an infinite vertical plate (ξ > 0) embedded in a saturated porous medium. MHD effect with uniform magnetic field B of strength B0 and small magnetic Reynolds number. Initially both the plate and fluid are at rest with constant temperature Θ∞. At time t = 0+ the plate originates oscillation in its plane ξ = 0 according to condition
After some time, plate temperature is raised to Θ w . The fluid is electrically conducting. Therefore, by Maxwell equations
By using Ohm’s law
The quantities ρ nf , μ e and σ are assumed constants. Magnetic field B is normal to V. The Reynolds number is so small that flow is laminar. Hence,
Equation for an incompressible Casson fluid flow53,54,55
Or
where π = e ab e ab and e ab is the (a, b)ah factor of the deformation rate, π is represent the product of the factor of deformation rate with itself, π c is represent the critical value of this product based on the non-Newtonian model, μ η is represent the plastic dynamic viscosity of the non- Newtonian fluid and P λ is yield stress of fluid. Under these conditions alongside with the assumption that the viscous dissipation term in the energy equation is neglected, we get the following system56:
where k* is absorption coefficient and σ* is Stefan-Boltzmann constant. Where Q0 is the heat generation term, ρ nf is the density of nanofluids, μ nf is the dynamic viscosity, u is the fluid velocity in the \(x\)-axis perpendicular direction, γ is the Casson fluid parameter, ψ(0 < ψ < 1), K > 0, ψ is the porous medium and K is the permeability of porous medium, h s is a constant heat transfer coefficient, Θ w is the constant plate temperature (Θ w < Θ∞, Θ w > Θ∞ due to the cooled or heated plate, respectively), g is the acceleration due to gravity, and β nf is the thermal expansion coefficient of the nanofluid.
Expressions for (ρc p ) nf , (ρβ) nf , μ nf , ρ nf , σ nf , k nf are given by24:
where ϕ the volume fraction of nano particles, ρ f and ρ s is represent the density of base fluid and particle respectively, and c p is specific heat on constant pressure. k nf , k f , and k s are the thermal conductivities of the nanofluid, the base-fluid, and the solid particles, respectively. The expressions of Eq. (10) are classified to nano particles57. For supplementary nano particles with unlike thermal conductivity, dynamic viscosity, see to Table 158,59,60.
the dimensionless variables are56,
where
where \(\frac{1}{K}\) is permeability of pours medium, M is the magnetic parameter, Gr is thermal Grashof number, Pr is Prandtl number, Nr is radiation parameter, and λ is Newtonian heating parameter.
Laplace Transform Solution
Laplace transforms of Eqs (12, 13) gives:
Eq. (16) using Eq. (17) gives:
After taking the inverse Laplace of Eq. (18):
Solution of Eq. (15) is:
Arranging Eq. (20) as:
where
Upon inversion:
where
Particular Cases
In order to link our found solutions with published literature, the following particular cases are examined by taking some parameters absent.
Making Gr = γ = 0 and Re = 1 in Eq. (22), reduces to:
which is identical to results of 61, Eq. (24).
Taking \(M=\frac{1}{k}=0\) in the above relation, we get:
Which is in accordance with61, Eq. (25).
Taking \(Gr=M=\frac{1}{k}=\frac{1}{\gamma }=0\), in Eq. (22), it moderates to:
Identical to58, Eq. (35).
Skin friction and Nusselt Number
Discussion
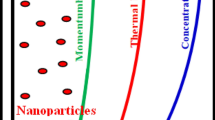
In this section different parameters including γ, ϕ, Gr, M, K, Pr, Nr Figs 2–11 are plotted. Geometry of problem is shown in Fig. 1. The influence of γ on u(y, t) which shows oscillatory behavior increasing first then decreasing is highlighted in Fig. 2.
Figures 3 and 4 show effects of ϕ on u(ξ, t) and θ(ξ, t).φ is take in between 0 ≤ ϕ ≤ 0.04 due to sedimentation when the range goes above from 0.08. It is observed in both cases if the nano particles volume fraction ϕ is increased it leads to the decreasing of temperature and velocity profile.
Figure 5 highlights the effect of Gr for Sodium alginate -based, Casson nanofluids on velocity profile. It is found that with increasing Gr, velocity increases. Because increasing effect in Gr, due to increase of buoyancy forces and decrease of viscous forces. Figure 6 the effect of M = 0, 1, 2 on the velocity profile. u(ξ, t) decreases due to increasing dragging force. M = 0, shows absence of MHD. Figure 7 shows K effect of on u(ξ, t). Velocity decrease due to decreasing friction. Figure 8 highlights that profile of velocity is increased with increasing radiation parameter Nr. The effect is studied for TiO2 nano particle.
The impact of two different types of nano particles (Al2O3 Sodium alginate -based Casson nanofluid and Ag-Sodium alginate -based nanofluid) on profile of velocity is studied in Fig. 9. The profile of velocity is greater for Al2O3 Sodium alginate -based Casson nanofluid and lower profile velocity for Ag-Sodium alginate -based nanofluid is observed.
Figure 10 highlights the comparison of both (Cu Sodium alginate -based Casson nanofluid and Ag-Sodium alginate -based nanofluid) on u(ξ, t). Velocity of Ag-Sodium alginate -based nanofluid is lower than copper Sodium alginate -based nanofluid. This shows that Cu nano particles have more thermal diffusivity compare to Ag which is physically true. Furthermore, the same comparison is study for Al2O3 and TiO2 models in Fig. 11, which shows that Aluminum oxide Al2O3 nano particles have high thermal diffusivity as compare to Titanium oxide TiO2.
Conclusion
The following remarks are concluded from this work:
-
u(ξ, t) decreases as γ increases
-
Temperature and velocity profile are decreasing with increasing nano particles volume
Fraction ϕ.
-
Al2O3 nanofluid has higher velocity from TiO2 nanofluid and Cu nanofluid has higher velocity from Ag nanofluid.
-
The pours medium K and MHD Μ show opposite behavior.
References
Makinde, O. D. & Mhone, P. Y. Heat transfer to MHD oscillatory flow in a channel filled with porous medium. Romanian Journal of Physics 50(9/10), 931 (2005).
Lissant, K. J. U.S. Patent No. 4,040,857. Washington, DC: U.S. Patent and Trademark Office (1977).
Aliseda, A. et al. Atomization of viscous and non-Newtonian liquids by a coaxial, high-speed gas jet. Experiments and droplet size modeling. International Journal of Multiphase Flow 34(2), 161–175 (2008).
Mehmood, A., Ali, A. & Mahmood, T. Unsteady magnetohydrodynamicoscillatory flow and heat transfer analysis of a viscous fluid in a porous channel filled with a saturated porous medium. Journal of Porous Media, 13(6) (2010).
Eldabe, N. T., Moatimid, G. M. & Ali, H. S. Magnetohydrodynamic flow of non-Newtonian visco-elastic fluid through a porous medium near an accelerated plate. Canadian Journal of Physics 81(11), 1249–1269 (2003).
Eldabe, N. T. & Sallam, S. N. Non-Darcy Couette flow through a porous medium of magnetohydro-dynamic visco-elastic fluid with heat and mass transfer. Canadian Journal of Physics 83(12), 1243–1265 (2005).
Hameed, M. & Nadeem, S. Unsteady MHD flow of a non-Newtonian fluid on a porous plate. Journal of Mathematical Analysis and Applications 325(1), 724–733 (2007).
Abolbashari, M. H., Freidoonimehr, N., Nazari, F. & Rashidi, M. M Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technology 267, 256–267 (2014).
Sheikholeslami, M., Ziabakhsh, Z. & Ganji, D. D. Transport of Magnetohydrodynamicnanofluid in a porous media. Colloids and Surfaces A. Physicochemical and Engineering Aspects 520, 201–212 (2017).
Sheikholeslami, M. & Ganji, D. D. Transportation of MHD nanofluid free convection in a porous semi annulus using numerical approach. Chemical Physics Letters 669, 202–210 (2017).
Sheikholeslami, M., Ganji, D. D. & Rashidi, M. M. Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation. Journal of the Taiwan Institute of Chemical Engineers 47, 6–17 (2015).
Sheikholeslami, M., Rashidi, M. M. & Ganji, D. D. Numerical investigation of magnetic nanofluid forced convective heat transfer in existence of variable magnetic field using two phase model. Journal of Molecular Liquids 212, 117–126 (2015).
Sheikholeslami, M., Rashidi, M. M. & Ganji, D. D. Effect of non-uniform magnetic field on forced convection heat transfer of–water nanofluid. Computer Methods in Applied Mechanics and Engineering 294, 299–312 (2015).
Sheikholeslami, M. & Ganji, D. D. Ferro hydrodynamic and magnetohydrodynamic effects on ferro fluid flow and convective heat transfer. Energy 75, 400–410 (2014).
Sheikholeslami, M., Ganji, D. D. & Rashidi, M. M. Magnetic field effect on unsteady nanofluid flow and heat transfer using Buongiorno model. Journal of Magnetism and Magnetic Materials 416, 164–173 (2016).
Sheikholeslami, M., Soleimani, S. & Ganji, D. D. Effect of electric field on hydrothermal behavior of nanofluid in a complex geometry. Journal of Molecular Liquids 213, 153–161 (2016).
Sheikholeslami, M. & Ganji, D. D. Numerical investigation of nanofluidtransportation in a curved cavity in existence of magnetic source. Chemical Physics Letters 667, 307–316 (2017).
Sheikholeslami, M. & Ganji, D. D. Numerical approach for magnetic nanofluidflow in a porous cavity using CuO nanoparticles. Materials & Design 120, 382–393 (2017).
Sheikholeslami, M. & Ganji, D. D. Free convection of Fe 3 O 4-water nanofluidunder the influence of an external magnetic source. Journal of Molecular Liquids 229, 530–540 (2017).
Sheikholeslami, M. & Ganji, D. D. Nanofluid convective heat transfer using semi analytical and numerical approaches: a review. Journal of the Taiwan Institute of Chemical Engineers 65, 43–77 (2016).
Sheikholeslami, M. & Ganji, D. D. Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Computer Methods in Applied Mechanics and Engineering 283, 651–663 (2015).
Sheikholeslami, M., Mustafa, M. T. & Ganji, D. D. Effect of Lorentz forces on forced-convection nanofluid flow over a stretched surface. Particuology 26, 108–113 (2016).
Sheikholeslami, M. & Ganji, D. D. Nanofluid hydrothermal behavior in existence of Lorentz forces considering Joule heating effect. Journal of Molecular Liquids 224, 526–537 (2016).
Sheikholeslami, M., Ganji, D. D. & Moradi, R. Forced convection in existence of Lorentz forces in a porous cavity with hot circular obstacle using nanofluid via Lattice Boltzmann method. Journal of Molecular Liquids 246, 103–111 (2017).
Sheikholeslami, M., Ganji, D. D. & Moradi, R. Heat transfer of Fe3O4–water nanofluid in a permeable medium with thermal radiation in existence of constant heat flux. Chemical Engineering Science 174, 326–336 (2017).
Sheikholeslami, M. & Ganji, D. D. Influence of magnetic field on CuO–H 2 O nanofluid flow considering Marangoni boundary layer. International Journal of Hydrogen Energy 42(5), 2748–2755 (2017).
Sheikholeslami, M., Nimafar, M. & Ganji, D. D. Analytical approach for the effect of melting heat transfer on nanofluid heat transfer. The European Physical Journal Plus 132(9), 385 (2017).
Sheikholeslami, M. & Ganji, D. D. Numerical analysis of nanofluidtransportation in porous media under the influence of external magnetic source. Journal of Molecular Liquids 233, 499–507 (2017).
Sheikholeslami, M., Nimafar, M. & Ganji, D. D. Nanofluid heat transfer betweentwo pipes considering Brownian motion using AGM. Alexandria Engineering Journal 56, 277–283 (2017).
Sheikholeslami, M. & Ganji, D. D. Impact of electric field on nanofluid forced convection heat transfer with considering variable properties. Journal of Molecular Liquids 229, 566–573 (2017).
Sheikholeslami, M. & Ganji, D. D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Physica A: Statistical Mechanics and its Applications 417, 273–286 (2015).
Putra, N., Thiesen, P. & Roetzel, W. Temperature dependence of thermal conductivity enhancement for nanofluids. Journal of Heat Transfer 125, 567–574 (2003).
Chol, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. ASME International Mechanical Engineering Congress & Exposition Publications 231, 99–106 (1995).
Karthik, V., Sahoo, S., Pabi, S. K. & Ghosh, S. On the photonic and electronic contribution to the enhanced thermal conductivity of water-based silver nanofluids. International Journal of Thermal Sciences 64, 53–61 (2013).
Eastman, J. A., Choi, S. U. S., Li, S., Yu, W. & Thompson, L. J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Applied Physics Letters 78(6), 718–720 (2001).
Li, Q., Xuan, Y. M., Jiang, J. & Xu, J. W. Experimental investigation on low andconvective heat transfer feature of a nanofluid for aerospace thermal management. YuhangXuebao Journal of Astronautics (China) 26(4), 391–394 (2005).
Heris, S. Z., Etemad, S. G. & Esfahany, M. N. Experimental investigation of oxide nanofluids laminar flow convective heat transfer. International Communications in Heat and Mass Transfer 33(4), 529–535 (2006).
Das, S. K., Choi, S. U., Yu, W., & Pradeep, T. Nanofluids: Science and technology. John Wiley & Sons. New Jersey (United States) (2007).
Faulkner, D. J., Rector, D. R., Davidson, J. J. & Shekarriz, R. Enhanced heat transfer through the use of nanofluids in forced convection. ASME International Mechanical Engineering Congress and Exposition, 1–6 (2004).
Lai, W. Y., Duculescu, B., Phelan, P. E. & Prasher, R. S. Convective heat transfer with nanofluids in a single 1.02-mm tube. ASME International Mechanical Engineering Congress and Exposition. 1–6 (2006).
Li, Q., Xuan, Y. & Wang, J. Investigation on convective heat transfer and flow features of nanofluids. Journal of Heat Transfer 125(2003), 151–155 (2003).
Oka, S. An Approach to α Unified Theory of the Flow Behavior of Time-Independent Non-Newtonian Suspensions. Japanese Journal of Applied Physics, 10( 3 ) (1971).
Ahmad, K., Hanouf, Z. & Ishak, A. MHD Cassonnanofluid flow past a wedge with Newtonian heating. The European Physical Journal Plus 132(2), 87 (2017).
Sarojamma, G. & Vendabai, K. Boundary layer flow of a Cassonnanofluid past a vertical exponentially stretching cylinder in the presence of a transverse magnetic field with internal heat generation/absorption. World Academy of Science, Engineering and Technology, International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 9(1), 138–143 (2015).
Khalid, A., Khan, I., Khan, A. & Shafie, S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Engineering Science and Technology, an International Journal 18(3), 309–317 (2015).
Bhattacharyya, K., Hayat, T. & Alsaedi, A. Analytic solution for magnetohydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer. Chinese Physics B 22(2), 024702 (2013).
Arthur, E. M., Seini, I. Y. & Bortteir, L. B. Analysis of Casson fluid flow over a vertical porous surface with chemical reaction in the presence of magnetic field. Journal of Applied Mathematics and Physics 3(06), 713 (2015).
Fetecau, C., Vieru, D. & Azhar, W. A. Natural Convection Flow of Fractional NanofluidsOver an Isothermal Vertical Plate with Thermal Radiation. Applied Sciences 7(3), 247 (2017).
Hussanan, A., Salleh, M. Z., Khan, I. & Tahar, R. M. Unsteady heat transfer flow of a Casson fluid with Newtonian heating and thermal radiation. JournalTeknologi 78(4), 1–7 (2016).
Ullah, I., Shafie, S. & Khan, I. Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium. Journal of King Saud University-Science 29(2), 250–259 (2017).
Hussanan, A., Salleh, M. Z., Khan, I. & Tahar, R. M. Heat Transfer in Magnetohydrodynamic Flow of a Casson Fluid with Porous Medium and Newtonian Heating. Journal of Nanofluids 6(4), 784–793 (2017).
Hayat, T., Khan, M. I., Waqas, M. & Alsaedi, A. Newtonian heating effect in nanofluid flow by a permeable cylinder. Results in Physics 7, 256–262 (2017).
Sheikholeslami, M. & Ellahi, R. Three dimensional microscopic simulation of magnetic field effect on natural convection of nanofluid. International Journal of Heat and Mass Transfer 89, 799–808 (2015).
Akbar, N. S., Raza, M. & Ellahi, R. Copper oxide nanoparticles analysis with water as base fluid for peristaltic flow in permeable tube with heat transfer. Computer Methods and Programs in Biomedicine 130, 22–30 (2016).
Oztop, H. F. & Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow 29(5), 1326–1336 (2008).
Khan, A., Khan, I. & Shafie, S. Effects of Newtonian heating and mass diffusion on HD free convection flow over vertical plate with shear stress at the wall. JournalTeknologi 78, 71–75 (2016).
Hussain, S. T., Khan, Z. H. & Nadeem, S. Water driven flow of carbon nanotubes in a rotating channel. Journal of Molecular Liquids 214, 136–144 (2016).
Khalid, A., Khan, I. & Shafie, S. Exact Solutions for Free Convection Flow of Nano Fluids with Ramped Wall Temperature. The European Physical Journal Plus 130(4), 1–14 (2015).
Hatami, M. & Ganji, D. D. Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders. Journal of molecular liquids. 188, 155–161 (2013).
Hatami, M. & Ganji, D. D. Natural convection of sodium alginate (SA) non-Newtonian nanofluid flow between two vertical flat plates by analytical and numerical methods. Case Studies in Thermal Engineering 2, 14–22 (2014).
Farhad, A., Khan, I. & Shafie, S. A Note on New Exact Solutions for some Unsteady Flows of Brinkman-Type Fluids over a Plane Wall. Zeitschriftfür Naturforschung A 67(6-7), 377–380 (2012).
Author information
Authors and Affiliations
Contributions
A.K. and I.K. designed the study; D.K. and F.K. conducted the experiments with technical assistance from F.A. and M.I.D.K. analyzed the data and wrote the paper; A.K., I.K. and M.I. provided general assistance. All authors have read and approved the final submission.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khan, A., Khan, D., Khan, I. et al. MHD Flow of Sodium Alginate-Based Casson Type Nanofluid Passing Through A Porous Medium With Newtonian Heating. Sci Rep 8, 8645 (2018). https://doi.org/10.1038/s41598-018-26994-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-26994-1
This article is cited by
-
Exploration of magnetically influenced flow dynamics of a dusty fluid induced by the ramped movement of a thermally active plate
Archive of Applied Mechanics (2024)
-
Computational simulation for MHD peristaltic transport of Jeffrey fluid with density-dependent parameters
Scientific Reports (2023)
-
Free convective trickling over a porous medium of fractional nanofluid with MHD and heat source/sink
Scientific Reports (2022)
-
Development of generalized Fourier and Fick’s law of electro-osmotic MHD flow of sodium alginate based Casson nanofluid through inclined microchannel: exact solution and entropy generation
Scientific Reports (2022)
-
Multi-generalized slip and ramped wall temperature effect on MHD Casson fluid: second law analysis
Journal of Thermal Analysis and Calorimetry (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.