Main

Quantum dots10—a nanoscale island containing a puddle of electrons—provide a highly tunable and simple setting to study the effects of large Coulomb interaction. They introduce level quantization and quantum interference in a controlled way, and can, in principle, be made in the very-low-density regime, where correlation effects are strong11. In addition, there are natural parallels between quantum dots and other confined systems of interacting particles, such as cold atoms in traps.

Therefore, we consider a model quantum dot consisting of electrons moving in a two-dimensional (2D) plane, with kinetic energy , and interacting with each other by long-range Coulomb repulsion (). Here electrons are labelled by i, their positions are ri, and all energies are expressed in atomic units, defined by ħ=e2/ε=m*=1 (with electronic charge e, effective mass m*, and dielectric constant ε). The electrons are confined by an external quadratic potential Vext(r)=(1/2)ω2r2 with circular symmetry and spring constant ω. The ratio between the strength of the Coulomb interaction and the kinetic energy is usually characterized by the interaction parameter rs≡(π n)−1/2, with n being the density of electrons. For our confined system in which n(r) varies, we define rs in the same way using the mean density . We have studied this system up to N=20 electrons. The spring constant ω makes the oscillator potential narrow (for large ω) or shallow (for small ω); it thereby tunes the average density of electrons between high and low values, thus controlling rs. For example, for N=20, varying ω between 3 and 0.0075 changes rs from 0.4 to 17.7. The radius of the dot grows significantly as rs increases, in an approximately linear fashion (see Fig. 1).

Figure 1: Electron density, n(r), for the ground state of an N=20 circular quantum dot (L=0, S=0).
figure 1

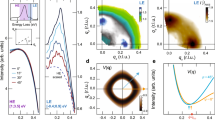
The extrapolated quantum Monte Carlo (QMC) estimator is used9. a, High density: rs≈0.4 (ω=3.0). b, Low density: rs≈15 (ω=0.01). Note the dramatic change in density profile with increasing rs: the electron–electron correlation caused by stronger interactions at low density produces sharp rings. The three-ring structure agrees with that seen in the classical limit. Note the significant increase in the radius of the dot for larger rs: it changes from approximately 2.75 to 80 (in atomic units) by increasing rs from 0.4 to 15. c, Radial cut of n(r) for rs≈10 (ω=0.02), where the three-ring structure is about to appear. The modulation is quantitatively characterized by the fractional peak height (FPH): draw the line tangential to the two outer peaks of n(r) (), then find the vertical line along which the distance from to n(r) is maximum, and finally define the FPH as the ratio of the two lengths . d, FPH as a function of rs for N=20 and 7. The curve for N=20 is linear and completely featureless for rs≲18. The solid line is a linear fit to the data. For smaller N, radial modulation in n(r) becomes stronger, leading to FPH→1 for large rs, and a deviation from linearity occurs (the dotted line ∼rs0.41 is the best fit for N=7). For our largest rs, the FPH typically grows with decreasing N, although not always monotonically. For example, FPH is largest for N=7, which yields a ‘perfect crystal’ with equidistant electrons, and thus produces a peak in the addition energy (see Fig. 3a). The Monte Carlo statistical error is less than the size of the points.

Full size image

In the bulk 2D electron gas, numerical work suggests a transition from a Fermi-liquid state to a Wigner crystal around rsc≈30–35 (refs 2–8). On the other hand, experiments on the 2D electron gas (which include, of course, disorder and residual effects of the ions) show more-complex behaviour, including evidence for a metal–insulator transition5.

Circular quantum dots have been studied previously using a variety of methods, yielding a largely inconclusive scenario. Many studies12,13,14 have used density functional theory or the Hartree–Fock method. These typically predict charge or spin-density-wave order even for modest rs (unless the symmetry is restored after the fact14), which are thought to be unphysical. Exact diagonalization calculations15,16 can be highly accurate but are restricted to small N and rs. Path-integral quantum Monte Carlo (PIMC) has also been applied: Egger et al. 17,18 found a crossover from Fermi liquid to ‘Wigner molecule’ at rs≈4—a value significantly smaller than the 2D bulk rsc. Another study19, using different criteria, found a two-stage transition for rs larger than rsc. Although PIMC treats interactions accurately, it has its own systematic and statistical problems; for instance, it generates a thermal average of states with different L and S quantum numbers, only preserving Sz symmetry. To avoid these various difficulties and to clarify the scenario, we have carried out a study using the variational Monte Carlo (VMC) and diffusion Monte Carlo (DMC) techniques9, which we used previously to study both circular20,21,22 and irregular23 dots at rs∼2. This method is free of the problems of PIMC but is approximate in that a ‘fixed-node’ error is made. We believe that the fixed-node error is small for the range of parameters studied here (see the Methods section, and the detailed comparison in the Supplementary Information).

Results for the electron density, n(r), are shown in Fig. 1. There is a dramatic change in n(r) on increasing interaction strength: for weak interactions (Fig. 1a), the density is rather homogeneous; the small modulation seen is caused by shell effects in the orbitals of the mean-field problem. In contrast, large rs induces strong radial modulation in n(r) (Fig. 1b), resulting in the formation of rings. Interestingly, for rs>10 the number of rings for each N is the same as that seen in the classical limit24,25 (), for example, three rings for N=20. In all of the cases we consider, the density n(r) is circularly symmetric, as is the density of spin-up and spin-down electrons separately, as required in two-dimensional systems, because we work with states of definite angular momentum L.

We find that the formation of rings, and the increase in their sharpness is completely smooth. This is shown quantitatively in Fig. 1d by using the fractional peak height (FPH, defined in Fig. 1c) of the outer ring to characterize the degree of structure. In the resulting curve for FPH as a function of rs, no deviations or special value of rs can be seen.

Having established the role of strong correlations in the formation of radial rings, which may be detectable in scanning-probe measurements, we turn to angular modulation—the issue of correlation-induced localization of the individual electrons in each of the circular rings. We therefore consider the pair densities gσ σ′(r0;r)—the probability of finding an electron with spin σ′ at location r when an electron with spin σ is held fixed at r0—and gT=g↑↑+g↑↓. In addition to radial rings, these detect any angular structure induced by the interactions.

The most prominent feature in the pair density is a hole around the location of the fixed electron. For unlike spins, it is caused purely by Coulomb repulsion (correlation hole), whereas for like spins the antisymmetry of the wavefunction plays an important role (exchange hole). For small rs, correlation is weak, so the hole in gσ,−σ is much smaller than that in gσ,σ. As rs increases, the correlation hole grows bigger, becoming the same size as the exchange hole around rs≈4–5.

Results for the pair density in the circular quantum dot are shown in Fig. 2 for an up-electron fixed on the outer ring. For N=20 at large rs, there are clear oscillations along the angular direction near r0. This signals ‘incipient’ Wigner localization. However, these oscillations are weak (weaker than the radial modulation) and short ranged (damped), indicating that long-range order is not yet established. As for radial modulation, the amplitude of the angular oscillations grows continuously, without any threshold value.

Figure 2: Pair density of the circular quantum dot with an up-electron fixed on the outer ring.
figure 2

a, g↑↓(r0;r) and b, g↑↑(r0;r) for the N=20 ground state (L=0, S=0) with rs≈15 (ω=0.01, r0=(57,0)). Short-range order develops near the fixed electron, indicating ‘incipient’ Wigner localization but not true long-range order. c, Evolution of angular oscillations along the outer ring with rs and N. The top trace shows 0.65×gT for rs≈6, N=20: although strong radial modulation has already appeared, leading to ‘ring formation’, there is almost no angular modulation. The middle trace is gT for rs≈15, N=20: clear angular structure is present, although compared with the ring modulation it is weak and short range. Spin-resolved angular structure is also shown here; note the peculiar bump at θ=π. The bottom trace is gT for rs≈16, N=6 (L=0, S=0): for small N, angular modulation is clearly stronger. (The y axis is shifted and scaled for N=20 for clarity.)

Full size image

The evolution of the angular oscillations as a function of rs and N is illustrated in Fig. 2c. Comparing the top two traces, for rs≈6 and 15 at N=20, we see that gT is almost featureless, even for an rs substantially larger than 1, whereas short-range oscillations have set in by our largest rs. The weakness of these oscillations suggests that electrons remain more or less delocalized along the ring for N=20, up to the largest rs studied. An intriguing feature of the spin-resolved pair densities shown is the bump at θ=π: g↑↑ decreases while g↑↓ increases. This feature is present for all rs≥4, and grows with increasing interaction strength; we have no explanation for it at this time. Turning now to smaller N, we find that two rings are present for N=6 at large rs: the outer ring has five electrons, whereas the remaining electron is at the centre. The lower trace in Fig. 2c shows that individual electrons are better localized for small N, a behaviour that we find holds quite generally.

Next, we turn our attention to the addition energy, Δ2E(N)=EG(N+1)+EG(N−1)−2EG(N), where EG(N) is the ground state energy of the dot with N electrons. This is accessible experimentally as the spacing between conductance peaks in a Coulomb blockade-transport measurement, and is given by the charging energy in the simplest model of a quantum dot10. Our results for Δ2E(N) (normalized by ω) for different interaction strengths are shown in Fig. 3 (rs for fixed ω varies slightly with N). For rs≈2, Δ2E(N) is similar to that of previous studies12,20,21: non-interacting ‘shell effects’ produce strong peaks for closed-shell configurations (N=6, 12, 20). At larger rs, the peaks weaken considerably, reducing mesoscopic fluctuations in Δ2E. For similar rs, shell effects are more strongly affected for small N, whereas their remnant persists for large N. For comparison, we plot the addition energy in the classical limit24,25 obtained from the ground-state energies in ref. 24. The remarkable similarity to our quantum result for small N at the largest rs is strong evidence for electron localization.

Figure 3: Ground-state energy.
figure 3

a, Addition energy (normalized) as a function of N for three different ω and for the classical limit24 . As interactions strengthen because of decreasing ω, the mesoscopic fluctuations in Δ2E become weaker. Note that this happens more readily in the small N limit. Features in the ω=0.01 trace at small N are remarkably similar to those found in the classical limit, showing that electrons are nearly localized for small N. (The zero of the y axis is offset for clarity, and the normalization of the classical trace is arbitrary.) b,c, gT for N=9, rs≈15 (ω=0.01), keeping an electron fixed on the outer ring (r0≈(37,0)), for L=0, S=3/2 (b, the usual ground state) and L=0, S=7/2 (c). Increasing rs, particularly for small N, often brings a strongly polarized state very close in energy to the ‘usual’ ground state. In the case shown, the two states become essentially degenerate (E=1.464651H*) within statistical errors. The extent of Wigner localization is clearly stronger for the S=7/2 state.

Full size image

Strong correlations can shuffle the energy ordering of different quantum states at fixed N. However, for ω>0.01, the ground state remains consistent with Hund’s first rule (except for N=3). For smaller ω, we see a tendency towards violation of this rule, primarily for small N (which, in general, are more affected by strong correlations), as in the following example. For N=9, the Hund’s rule ground state has (L,S)=(0,3/2). We find that for ω=0.01, the highly polarized state (0,7/2) becomes degenerate with the usual ground state (within our numerical accuracy). (All other (L,S) states lie higher in energy.) Note that S=7/2 requires promotion between non-interacting shells, and so lies much higher in energy in the weakly interacting limit. At large rs, this difference is overcome by the gain in interaction energy. The pair density gT for both these N=9 states is shown in Fig. 3. The more-polarized state is clearly more localized; we find that, as expected, this is generally the case because exchange keeps the electrons apart.

The scenario that emerges here is significantly different from that for the bulk. The gradual emergence of the radial oscillations is connected to the fact that the translational symmetry is necessarily broken, and so the interactions can readily amplify existing inhomogeneities. The development of the addition-energy curves further supports this point: the structure caused by quantum interference is rapidly suppressed by the interactions leading to surprisingly smooth behaviour over a wide range of rs. Thus, strong correlations and incipient localization should be taken into account for a very broad range of interaction strength.

Methods

As a starting point, we use the Kohn–Sham orbitals obtained from a density functional calculation done in the local density approximation. We then carry out a VMC calculation using a trial wavefunction, ΨT, which is a linear combination of products of up- and down-spin Slater determinants of the Kohn–Sham orbitals multiplied by a Jastrow factor. The Jastrow factor effectively describes the dynamic correlation between the electrons coming from their mutual repulsion, whereas the near-degeneracy correlation is taken into account by having more than one determinant. We optimize the Jastrow parameters and determinant coefficients by minimizing the variance of the local energy26,27. Finally, we use fixed-node DMC calculations9,28 to project the optimized many-body wavefunction onto a better approximation of the true ground state, an approximation that has the same nodes as ΨT.

The fixed-node DMC energy is an upper bound to the true energy, and only depends on the nodes of the trial wavefunction obtained from VMC. We have calculated the energy E(N,L,S) of a circular quantum dot for each N with angular momentum L and spin S—all good quantum numbers for our model. (Sz is also a good quantum number, and all our calculations are done for Sz=S; however, E is independent of Sz.) We investigated all possible combinations of L and S for the low-lying states, and the combination yielding the lowest DMC energy, EG, was taken as the ground state for that N. For expectation values of operators that do not commute with the hamiltonian—for example, the density or the pair density—we use an extrapolated estimator9,29 (denoted FQMC for an operator F), which eliminates the inaccuracy coming from the first-order error in the trial wavefunction. FQMC is defined as 2FDMC−FVMC when FDMC≥FVMC, and as FDMC2/FVMC otherwise.

In the multi-determinant expansion of ΨT, we only keep Slater determinants formed from the lowest energy Kohn–Sham orbitals for all of the results shown here. Our study is currently limited to rs≤18 for technical reasons. The most serious is the failure of the VMC optimization, as many Slater determinants need to be included for stronger interactions.

For two cases, corresponding to one moderate and one large rs, we have done preliminary calculations with higher orbitals by including all determinants involving promotion of two electrons across a shell gap (10 configuration-state functions for N=20). This allows for a change in the nodes of ΨT. We find that the change in the energy, as well as the change in density and pair density, is small, although somewhat larger for greater rs. Thus, we believe that the fixed-node error in our calculations is under control.