Measurement of the tilt of a moving domain wall shows precession-free dynamics in compensated ferrimagnets

Abstract

One fundamental obstacle to efficient ferromagnetic spintronics is magnetic precession, which intrinsically limits the dynamics of magnetic textures. We experimentally demonstrate that this precession vanishes when the net angular momentum is compensated in domain walls driven by spin–orbit torque in a ferrimagnetic GdFeCo/Pt track. We use transverse in-plane fields to provide a robust and parameter-free measurement of the domain wall internal magnetisation angle, demonstrating that, at the angular compensation, the DW tilt is zero, and thus the magnetic precession that caused it is suppressed. Our results highlight the mechanism of faster and more efficient dynamics in materials with multiple spin lattices and vanishing net angular momentum, promising for high-speed, low-power spintronic applications.

Introduction

In magnetic materials, the exchange interaction aligns the magnetic moments producing ferromagnetic or antiferromagnetic orders. Even if ferromagnets have numerous applications in spintronics, two effects limit the development of higher-density and faster devices. Firstly, the stray fields couple adjacent magnetic textures and limit their density. Secondly, the magnetic precession changes the internal magnetisation of moving textures, resulting in e.g. a continuous precession in field- or spin-transfer-torque-driven DWs above Walker threshold^1,2,3, in a steady-state internal angle in SOT-driven DWs^4,5, or in the topological deflection of skyrmions^6,7,8,9. All these effects limit the texture’s velocity. Antiferromagnetic order leads to faster dynamics and robustness against spurious fields, and is emerging as a new paradigm for spintronics¹⁰. However, perfect antiferromagnets with exactly compensated magnetic sub-lattices are hard to probe and manipulate, and therefore have been rarely studied or used in applications. Rare Earth-Transition Metal (RETM) ferrimagnetic alloys allow to benefit from both antiferromagnetic-like dynamics and ferromagnetic-like spintronic properties. Indeed, they have two antiferromagnetically-coupled sublattices, corresponding roughly to the RE and TM moments, and their spin transport is carried mainly by the TM sub-lattice¹¹. Furthermore, RETM thin films can exhibit perpendicular magnetic anisotropy, are conductors, and present large spin transport polarization and spin torques, even when integrated in complex stacks¹². Additionally, their magnetic properties can be controlled by changing either their composition or temperature, as described by the mean-field theory¹¹. For a given composition, they can exhibit two characteristic temperatures: the angular momentum compensation temperature (T_AC) and the magnetic compensation temperature (T_MC), for which the net angular momentum or the net magnetisation (M_S) are respectively zero (Fig. 1b). Interestingly, due to the different Landé factors of RE and TM, these two temperatures are different (with T_MC < T_AC for GdFeCo). At T_MC, the magnetostatic response vanishes (as observed in the divergence of the coercivity, anisotropy field, …). In contrast, at T_AC the dynamics is affected. Although these effects are challenging to evidence, the singular and promising behaviour of RETM at T_AC was observed in current-induced switching¹³, magnetic resonance¹⁴, and time-resolved laser pump-probe measurements^15,16. In very recent reports the signature of the dynamics at T_AC was assigned to a DW mobility peak, under field^17,18, under current by spin–orbit torques (SOT)^19,20,21,22, or by spin transfer torque²³. However, even if this mobility peak is a signature of angular compensation, it is affected by the strong sensitivity of DW propagation to Joule heating and pinning^24,25. Furthermore, none of the latter experiments gives a direct access to the internal DW magnetisation angle that is an intrinsic signature of the magnetisation precession. In this paper, we use a robust measurement of the variation of the DW velocity with a transverse bias field to determine the DW internal magnetisation angle across the compensation temperatures, and we show that there is no DW magnetisation tilt, and therefore no magnetic precession, at the angular moment compensation.

Figure 1

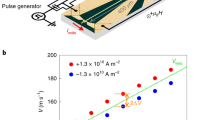
GdFeCo/Pt sample properties and SOT-driven DW propagation in tracks. (a) Sketch of the track containing a SOT-driven DW and of the magnetisation of the two sublattices (in red and blue) below T_MC. The size of the arrows represents their relative magnitude. The grayscale corresponds to the domain Kerr contrast while the DW is depicted in white. The angle of the DW magnetisation is given by φ. (b) Measured net magnetisation M_S (squares) of the virgin film and coercivity H_C (dots) of the patterned track versus temperature T. The M_S points were shifted by − 31 K to account for migration of Gd during patterning¹². The continuous line is the result of the mean-field model (see suppl.). (c) Kerr images of a DW driven by 300 GA/m², 25 ns current pulses in at temperature set-point of T_SP = 300 K. (d) (J,T_sp) colour-plot of measured mobilities (black points). Stars mark the peak of mobility µ versus T_SP (interpolated; see suppl.). The solid line is a quadratic fit of the maximum mobilities, with 345 K = T_SP + k J² (k = 1.3 10^–4 K/(GA m⁻²)²).

Results

DWs driven by SOT have been observed in thin ferrimagnetic films with a heavy-metal adjacent layer, like Pt, which induces three main interfacial effects: perpendicular anisotropy, Dzyaloshinskii-Moriya exchange interaction (DMI), and vertical spin current generated by the spin Hall effect (SHE) (Fig. 1a). Such systems present chiral Néel DWs^26,27, which is the configuration for which the SOT DW driving is most effective (Fig. 1a)⁴.

To investigate SOT-driven DW dynamics in RETM, a 10 µm-wide track of amorphous Gd_.4(Fe_.85Co_.15)_0.6 (5 nm) capped with Pt (7 nm) with perpendicular magnetic anisotropy was fabricated (Fig. 1a). Ms(T) was measured by SQUID magnetometry (Fig. 1b). Due to the migration of Gd during patterning¹² the M_S values have changed. By measuring the T_MC pre- and post-patterning, we corrected this M_S temperature shift of − 31 K. A relatively low and temperature-dependent magnetisation has been measured as expected¹². The magnetic compensation temperature where the net magnetisation vanishes is clearly visible. Transport measurements of the extraordinary Hall effect (EHE) versus field were made on 5 μm wide crosses at different temperatures for both in-plane and out-of-plane magnetic fields. The T_MC of the track, 312 K, was determined by measuring the coercivity divergence (Fig. 1b). It diverges at T_MC as the applied field produces opposite and balanced effects on the two compensated sub-networks. The magnitude of the SOT was determined with the second harmonic Hall voltage method^28,29.

DW velocity measurements were performed using a Kerr microscope with a controlled temperature sample holder (at temperature set-point T_SP). 25 ns pulses of current density J were applied in the track containing a DW. After each pulse, a Kerr image is recorded. The DWs move against the electron flow, which is compatible with SOT-driving of chiral Néel DWs with the same relative sign of DMI and SHE as the one found in ferromagnetic Pt/Co^4,30 and which rules out any significant spin-transfer torque²⁵. The linearity of the DW displacement with the pulse number and duration (see suppl.) allows the robust determination of the propagation velocity v. The magnitude of DMI was determined by analysing the DW velocity driven by electrical current under an in-plane field (H_x) collinear to the current³¹ (see suppl.). Since in perpendicularly-magnetised tracks SOT induced propagation depends on the DW in-plane magnetisation, the reversal of the DW propagation induced by the in-plane field also validates the SOT-driven mechanism.

High DW velocities (> 700 m/s; see velocity curves in suppl.) are observed for low J (~ 600 GA/m²), as previously reported in similar alloys^19,20. The DW mobility µ = v/J exhibits a peak that depends on the T_SP and the current density J. Figure 1d shows measured mobilities in a (J,T_sp) colour-plot, and for each J the maximum µ is marked with a star. The coordinates of the maxima µ follow $T - T_{SP} \propto J^{2}$ (solid line in Fig. 1c), which suggests that they all occur at a single track temperature T = 345 K. In ferromagnets, models predict that the SOT-driven DW steady-state velocity follows

$$ v/J \propto \cos \left( \varphi \right) $$

(1)

where $\varphi$ is the angle of the internal DW magnetisation⁴. The angle φ is determined by the balance between DMI, which favours the Néel configuration (φ = 0), and the precession induced by SOT, which increases $\left| \varphi \right|$. In ferrimagnets, it is expected that the precession depends on temperature and vanishes at T_AC with a peak in velocity (See suppl.). If the effects of pinning and Joule heating are neglected, it is possible to attribute the observed mobility peak with minimal $\left| \varphi \right|$, and it can be deduced that the temperature of the maxima is T_AC (345 K according to the fit in Fig. 1c), as previously done in Refs.^19,20.

In order to overcome these limitations, we propose a new method based on the application of a transverse field H_Y that reveals the internal magnetic dynamics of the DW. It provides both a qualitative and quantitative evaluation of $\varphi$, including its sign, across both compensation points, without requiring any additional sample magnetic parameters. Simultaneously, it determines the Joule heating amplitude.

We measured the DW velocity v versus T_SP with an applied in-plane field H_Y perpendicular to the current flow (see inset of Fig. 2a). Figure 2a shows the velocity v(T_SP, H_Y) without field (µ₀H_Y = 0) and with two opposite fields (µ₀H_Y =  ± 90 mT) for positive and negative current density (J =  ± 360 GA/m²). Whatever the H_Y field, the DW moves along the current direction. Two crossing points, at T_SP = 300 K and T_SP = 328 K, are observed where v(T_SP, + H_Y) = v(T_SP, − H_Y). On the first crossing point, the velocity without field is the same as with field, v(300 K, 0) = v(300 K, ± H_Y), while on the second crossing point the velocity without field is larger than with field, v(328 K, 0) > v(328 K, ± H_Y). The crossing points are more readily distinguished by plotting Δv(T_SP) ≡ v(T_SP, + H_Y) − v(T_SP, − H_Y), shown in Fig. 2b, and are the same for both current polarities.

Figure 2

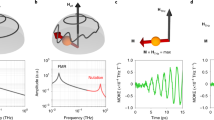
SOT-driven DW under H_Y: determination of the internal DW dynamics, T_MC and T_AC. (a) Measured DW velocity v versus sample holder set-point temperature T_SP with µ₀H_Y =  ± 90 mT or 0 mT, for J =  ± 360 GA/m². (b) Velocity difference Δv(T_SP) ≡ v(J, + H_Y) − v(J,-H_Y) from (a). (c) Diagram of the sublattice orientations in a SOT-driven DW under H_Y across compensation points. The red and blue arrows correspond to RE and TM, respectively. (d) Colour-plot of Δv/‹v›(J, T_SP). Black points correspond to measurements. Grey circles correspond to crossing points where Δv = 0 (see (a)). The black lines are parabolic fits of these crossing points (T = T_SP + k J², k = 0.8 10^–4 K/(GA/m²)², T_MC = 312 K, T_AC = 334 K). Above, the action of the SOT on the internal DW angle $\varphi_{J}$ is sketched, to illustrate the sense of rotation of $\varphi_{J}$ without field. Throughout, pink and green backgrounds mark the sign of Δv.

To understand the effect of H_Y on SOT-driven DWs in ferrimagnets, we first consider the well-understood ferromagnetic case. The H_Y couples to the internal magnetisation of the DW and changes the equilibrium φ. As v/J ∝ cos(φ) (Eq. 1), if + H_Y rotates φ closer to Néel configuration, it will increase the velocity. The sign of Δv shows whether + H_Y rotates φ closer to or farther from the Néel configuration compared to − H_Y. In particular, a positive Δv means that + H_Y and J have opposite contributions to φ (and Δv < 0 means + H_Y and J push φ in the same direction). Since the sign of the effect of H_Y is known, we can deduce the sign of the φ angle without field, that we note φ_J.

In the RETM ferrimagnetic case, the DW velocity can still be described with the same model³². Since the spin current interacts mainly with the TM sub-lattice (¹²and references therein), φ in Eq. (1) corresponds to the DW angle of the TM sub-lattice (see Fig. 1a). The Zeeman contribution of H_Y depends now on the net magnetisation M_S = M_TM − M_RE, which changes sign at T_MC.

Figure 2c shows a sketch of the in-plane magnetisation of the RE and TM sublattices at the centre of the SOT-driven DW at different temperatures. At T < T_MC, the RE sublattice is dominant (M_TM < M_RE) and + H_Y rotates φ clockwise. At T = T_MC, M_RE = M_TM and H_Y does not affect φ nor v, and v(H_Y = 0) = v(± H_Y). Above T_MC, M_TM > M_RE and the effect of external fields is reversed: + H_Y rotates φ counterclockwise.

In Fig. 2b, Δv < 0 below T_SP = 300 K, so we conclude that the current acts on φ in the same direction as + H_Y, i.e. φ_J < 0. We observe that T_MC occurs at T_SP = 300 K, as v(H_Y = 0) = v(± H_Y). At this point, it is not possible to determine the φ_J. Above T_MC, interestingly, the measured Δv crosses zero once more (T_SP = 328 K). Below this point, Δv > 0 so φ_J < 0, and above it Δv < 0 so φ_J > 0. At the crossing point, the current does not affect φ: φ_J = 0. The fact that the velocity with ± H_Y are smaller than without field confirms the symmetrical configuration shown in Fig. 2c with φ_J = 0 (see suppl. mat. for other values of H_Y). The observed reversal of the direction of the precession, and the precession-free point, is characteristic of the angular compensation, T_AC.

We measured this quantity for different current densities and the obtained behaviour is very similar. Figure 2d shows all measured Δv/‹v› in a colour-plot as a function of T_SP and J, normalized by the average velocity with + H_Y and -H_Y. This normalization removes the first-order dependence on |J| of Eq. (1) ($v \propto \cdot J \cdot \cos \varphi \left( J \right)$), as ${\Delta }v/v = 2\frac{{\cos \left( {\varphi_{{ + H_{Y} }} } \right) - \cos \left( {\varphi_{{ - H_{Y} }} } \right)}}{{\cos \left( {\varphi_{{ + H_{Y} }} } \right) + \cos \left( {\varphi_{{ - H_{Y} }} } \right)}}$ is independent of J, enabling the direct comparison of data for different current densities. Three regions can be observed with, successively, Δv < 0, Δv > 0 and Δv < 0, separated by the two sets of crossing points. These crossing points depend on J but their difference is independent of J (see data in suppl.). Indeed, both follow a Joule heating parabolic relation with same heating parameter (within 1%), which can be associated to the isothermal lines of T_MC = 312 K and T_AC = 334 K. These observations hold for different magnitudes of H_Y (see suppl.). Also, spurious external fields have low impact on the crossing points (see calculations in suppl.). Note that T_MC and T_AC are consistent with the previous measurements of H_C(T) in Fig. 1b (T_MC = 312 K) and µ(J) in Fig. 1d (T_AC = 345 K). Furthermore, the measured values of Δv are large (few hundreds of m/s), give directly the sense of precession of the magnetisation and show that the angle $\varphi$ of the moving DW changes sign and vanishes at T_AC.

Discussion

In ferromagnets, the angle φ can be described with the 1D model⁴, extended to include external magnetic fields:

$$ \varphi = \arctan \left( {\frac{\Delta }{D}\left( {\frac{{ \hbar \theta_{SHE} }}{2\,e t}\frac{ J}{\alpha } + \mu_{0} {\text{M}}_{s} {\text{H}}_{y} } \right)} \right) $$

(2)

where $\Delta$ is the DW width parameter, D is the DMI parameter, $\alpha$ is the Gilbert damping parameter, ħ is the reduced Planck constant, e is the fundamental charge, θ_SHE is the spin Hall angle of the Pt layer, and t is the magnetic film thickness. For a ferrimagnet, $\varphi$ corresponds to the DW angle of the TM sub-lattice (see Fig. 1a), M_S to the net magnetisation, and α is the effective Gilbert damping parameter. The observed reversal and vanishing of the precession dynamics (φ_J = 0) at T_AC is directly associated with a divergence and change of sign of this effective Gilbert damping parameter α(T) in Eq. (2), as described in Refs.^15,16,33 (Note that in Ref.¹⁷ it is stated that the α parameter does not diverge at T_AC. However, the authors refer to their new and distinct definition of α that is not the conventional Gilbert’s parameter. Gilbert’s α does diverge, as it is discussed briefly in Ref.¹⁷). Note that, even if α diverges and changes sign, the dissipation power, which is proportional to the product of α and the net angular momentum, remains finite and positive even across T_AC. This effective parameter approach was successfully used to describe ferrimagnetic dynamics observations^15,16,20,34.

Figure 3a,b show analytical calculations of the DW angle φ and related velocity v as a function of T and H_Y. All material parameters were taken from measurements (see Fig. 1b,c and suppl.), except for effective damping parameter α(T) which was approximated by $\propto$ 1/(T − T_AC) to account the expected divergence at T_AC. All other quantities (Δ, D, θ_SHE) are taken as constant in the narrow investigated range. We observe an excellent agreement between the theoretical curves and the experimental data in Fig. 2a. We can also verify the explanation given above (Fig. 2c): at T_MC, the φ and v are the same for all H_Y and, at T_AC, φ are opposite for + H_Y and − H_Y.

Figure 3

taken from measurements (see Fig. 1b,c and suppl.). µ₀H_Y =  ± 90 mT, and J =  ± 360 GA/m². (c) Experimental Δv/‹v› for different current densities. The thin lines correspond to fits using a simplified version of Eq. (2) (see text). The data were horizontally shifted so that their first crossing points are juxtaposed at T_MC = 312 K. (d) Obtained φ_J from the fits in (c). The thick lines and envelopes in (c) and (d) correspond to the theoretical curves, obtained with the same parameters of (a) and (b).

Determination of the internal DW angle. (a, b) Calculated φ and v according to Eqs. (1), (2), using the material parameters

All Δv/‹v› are shown in the same graph versus T in Fig. 3c. Since we know that all the first crossing points occur at the same track temperature (T_MC = 312 K), we shifted all the curves in Fig. 3c so the crossing points overlap at T_MC. Note that, for a given J, Δv/‹v› is only a function of φ(+ H_y) and φ(− H_y), with no other parameters²⁸. We use the approximation of $\alpha \propto 1/\left( {T - T_{AC} } \right)$ and $M_{S} \propto T - T_{MC}$ to get a simplified version of Eq. (2): $\varphi \left( {T, \pm H_{Y} } \right) = \arctan \left( {Ja\left( {T - T_{a} } \right) \pm H_{Y} b\left( {T - T_{b} } \right)} \right)$, that is used to fit the Δv/‹v› points for each current density (thin lines in Figs. 3c,d). The first term corresponds to the current contribution, and should change sign at T_AC, as the effective damping does, and the second term should change sign at T_MC, like M_S. The fitting indeed gives T_a = 336 ± 3 K ≈ T_AC, T_b = 312 ± 2 K ≈ T_MC (and a = − (0.3 ± 0.1) 10^–3 (K·GAm⁻²)⁻¹ and b = − 0.04 ± 0.01 (K·T)⁻¹). We plot the temperature evolution of φ_J in Fig. 3d, obtained directly from a and T_a. Without field, the angle φ_J follows the sketch of Fig. 2c, and is in agreement with the theoretical curve of Fig. 3a. All data Δv/‹v› (Fig. 3c) and the fitted φ_J (Fig. 3d) are in the envelope that corresponds to the theoretical curve for J between 150 and 450 GA/m².

In GdFeCo/Pt with Néel DWs and DMI, we measured how the velocity of an SOT-driven DW changes with an in-plane transverse bias field H_y. This bias field changes the internal angle of the magnetisation of the DW (φ_J) that affects its velocity (v ~ cos φ_J). By analysing the sign of the velocity difference with + H_y and—H_y (Δv), it is possible to determine the sign of φ_J. We found that there are two temperatures for which Δv = 0 and we showed that they correspond to the T_MC and T_AC. These measurements also reveal the vanishing of the tilt of the magnetisation at T_AC (φ_J = 0), which had been theoretically predicted but never directly observed. This novel approach determines precisely the magnitude and the sense of the DW tilt for a moving DW, which is a consequence of the magnetic precession of the spins through which the DW travels. This method gives T_MC and T_AC and is based on the intrinsic DW dynamics and so is unaffected by DW pinning. Finally, the velocity difference is easily observed (Δv ≈ 100 m/s), independent of the Joule heating and does not require knowledge of material parameters.

The suppression of magnetic precession opens new perspectives for fast and energy-efficient spintronics using any angular-momentum-compensated multi-lattice material. It induces a maximum of SOT-driven DW mobility in a compensated RETM ferrimagnet, as we observed in agreement with previous reports^19,20,21. Here, for the first time, direct experimental evidence is provided that the SOT-driven DW propagation is tilt-free and the DW remains Néel (φ = 0) in angular momentum compensated ferrimagnets. These dynamics in angular-momentum-compensated materials are also interesting for skyrmion dynamics, and it has been shown that it leads to efficient manipulations³⁵, and vanishing topological deflection²².

Materials and methods

Sample deposition, fabrication

The film of amorphous GdFeCo(5 nm) capped with Pt(7 nm) was deposited by electron beam co-evaporation in ultrahigh vacuum on thermally-oxidised Si substrates. Details of the film growth and characterisation can be found in¹². The tracks were patterned by e-beam lithography and hard-mask ion-beam etching.

Characterisation of the magnetic properties

Transport measurements of the extraordinary Hall effect versus field were made on 5 μm crosses at different temperatures in a commercial QD PPMS. The magnitude of the SOT equivalent field H_DL was determined with the harmonic voltage method^28,29. M_S(T) was measured by SQUID magnetometry. The magnitude of DMI equivalent field H_DMI was determined by analysing the SOT-driven DW velocity with a field collinear to the current as in³¹.

Kerr microscopy

Kerr microscopy experiments were performed using an adapted commercial Schafer Kerr microscope, with a temperature regulated sample holder. The DW velocity was measured by taking Kerr images before and after each of about ten current pulses (see Fig. 1c). The linearity of the DW displacement with the number of pulses and with the pulse duration allowed a reliable determination of the propagation velocity v.

Analytical model of DW velocity under SOT and field

Equations (1) and (2) and the theoretical plots in Figs. 2 and 3, were done using the 1D model described in⁴ in the steady-state regime ($\dot{\varphi } = 0$), extended to include external magnetic fields and neglecting the in-plane demagnetisation field:

$$ \left\{ {\begin{array}{ll} {\frac{\alpha v}{\Delta } = \gamma_{0} \left( {H_{Z} + \frac{\pi }{2}H_{SHE} \cos \varphi } \right)} \\ {\frac{v}{\Delta } = \gamma_{0} \frac{\pi }{2}\left( {\left( {H_{DMI} + H_{X} } \right)\sin \varphi + H_{Y} \cos \varphi } \right)} \\ \end{array} } \right. $$

with $H_{SHE} = \frac{\hbar }{2e}\frac{{\theta_{SHE} }}{{\mu_{0} M_{S} t}}J,\;H_{DMI} = \frac{D}{{\Delta \mu_{0} M_{S} }}$. In the absence of H_Z, this yields $v = \frac{{\gamma_{0} \Delta }}{\alpha } \frac{\pi }{2}H_{SHE} \cos \varphi$, $\varphi = \tan \left( {\frac{{H_{SHE} /\alpha + H_{Y} }}{{H_{DMI} + H_{X} }}} \right)$. These equations can be used for ferrimagnets using the effective parameters^15,16,33 as described above. The calculated plots in Fig. 3 are obtained using a constant ratio D/Δ obtained from the determination of H_DMI $\left( {\frac{D}{\Delta } = \mu_{0} M_{S} \left( T \right)H_{DMI} \left( T \right) = 2 \;{\text{kJ}}/{\text{m}}^{3} } \right)$, and the SOT factor $\frac{\hbar }{2e}\frac{{\theta_{SHE} }}{t}$ from the determination of H_DL (ℏ θ_SHE/(2 e t) = µ₀ M_S(T) H_DL(T)/J = 4.0 J·m⁻³/(GA·m⁻²)). The only parameter that is not experimentally determined, α(T), is approximated by an inverse linear law α(T) = 13.0 K/(T − T_AC), chosen to best reproduce the shape of the experimental curves (see Figs. 2a and 3b). See supplementary materials for more results.