Introduction

The advent of optical quantum information processing has placed stringent requirements on the ability to handle nonclassical states such as single-photon and entangled states. At variance with weak coherent light beams, which can also be used as pseudo–photon sources, single-photon Fock states either on demand or heralded guarantee conditional security, e.g., in quantum cryptography1 and are crucial in optical information processing2,3,4,5. Single-photon entangled states, in particular, can be generated and employed, e.g., for teleportation6 and linear optics quantum computation7. This is a basic form of entanglement and it is in principle isomorphic to any other kind of two-photon entanglement8,9.

Single-photon spatial entanglement, e.g., is attained by splitting a single-photon Fock state on a 50/50 beam splitter. Because the photon itself cannot be split, quantum mechanics prescribes that the photon must take both paths at once, thereby entangling the two spatial modes at the outputs of the beam-splitter. Such a single-photon entangled state realizes an optical qubit, where information can be encoded. Single-photon frequency entanglement can also be exploited to realize frequency qubit encoding10, which uses discrete orthogonal modes in the frequency domain rather than spatial modes. This kind of encoding appears more suitable to multi-mode entanglement11,12 and quantum information can benefit from multi-frequency encoding in much the same way as classical communication has from the introduction of frequency multiplexing.

We here show that single-photon frequency entanglement can be efficiently controlled trough an interface made of an optically dense sample of cold atoms. This would be crucial toward the realization of quantum memories that work with single-photon multimode entangled states2; in the following we specifically illustrate the case of a single-photon two-mode frequency entangled state of the form,

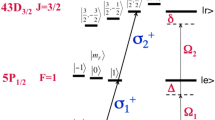
The photon excitation is simultaneously shared by two atomic transitions of frequency ωp and ωm (See Fig. 1), with |0m, 1p〉 and |1m, 0p〉 being the states with the photon created in one or the other frequency mode, whose phase relation should remain fixed to preserve entanglement through the interface. The state |Φe〉, an archetype of frequency entanglement, can be conditionally generated by standard techniques using parametric downconversion where a crystal with χ(2) nonlinearity is pumped at two different frequencies13. A signal and idler photon pair is generated in two different spatial directions and detection of one idler photon heralds the presence of a photon along the signal path. Indistinguishability between which pump has generated the photon pair leads to the superposition state (1), with the two possible alternatives of a single-photon with frequency ωm and ωp and with a relative phase ϕη set by the generation scheme. It is worth noting that standard optical manipulations can be used to convert |Φe〉 into a familiar single-photon spatialmode entangled state, namely through a unitary operation which redefines the state into a truly nonlocal entanglement14.

Figure 1
figure 1

Atomic interface for a single-photon frequency-bin entangled state.

A sample of cold atoms loaded into a magneto-optical trap (MOT) and initially pumped to state |1〉 is used as interface. Two continuous strong coupling beams ωcm and ωcp, with the same polarization and Rabi frequency Ωc but different detunings from the excited state |2〉, control the coupling of the frequency entangled state (1) to the interface. The relevant wavepacket of length and bandwidth such that is double Λ-resonant with the coupling beams (ωm − ωcm = ωp − ωcp) through a nearly-resonant () and a far off-resonant () (Raman) transition between the two hyperfine electronic ground states |1〉 and |3〉. Under such conditions non-resonantly excited coherences30 can be neglected and control of the entangled state is described by the closed set of coupled equations (2–3). The energy level scheme corresponds to the D2 line in 87Rb (52S1/2 → 52P3/2) with a transition wavelength λ21 = 780.24 nm. Hyperfine ground state dephasing and excited state relaxation rate are γ3 = 2π × 1 kHz and γ2 = 2π × 6 MHz.

Full size image

Routing the entangled state (1) requires a very good degree of control over the photon propagation and most importantly over the photon's quantum state. Routing has to preserve entanglement, in fact and should perform sufficiently large and flexible delays to be useful in all-optical processing. We show that this can be achieved through a phase-resonant excitation mechanism of an atomic interface where the two constraints above can be satisfied. The mechanism mainly relies, in contrast to previous studies15, on dark-state matching effects which make our single-photon two-mode frequency entangled state particularly easy to control.

The underpinning features of the interface can be understood by considering an ultracold sample of N atoms placed at random positions in a volume V in the three-level double-Λ interaction scheme16 described in Fig. 1. The interface coupling dynamics is studied by considering for each of the two frequency-bins a weak quasi-monochromatic field with mean frequency ωm and ωp and corresponding wave-number km and kp. In the plane-wave representation the field amplitude operator comprises a finite number of modes each described by Heisenberg photon annihilation operators17. In such a narrow-band approximation and to the lowest order in the (weak) field this is found to obey the equation of motion,

where is the complex detuning expressed in terms of the excited state decay rate (γ2) while , with d12 the electric-dipole matrix element between the states |1〉 and |2〉. A similar result obtains for the other mode operator . The two fields are taken here with the same polarization . The operator on the right hand side of (2) describes a collective atomic excitation and can likewise be expressed in terms of a quasi-monochromatic plane-wave expansions of atomic Heisenberg operators. The relevant evolution equation is,

where and is expressed in terms of the two hyperfine ground levels dephasing (γ3). The last term within brackets is obtained from the previous one with the interchange . Upon Fourier transforming (2–3) in time one is left with a set of coupled eq.s describing the spatial evolution of the two modes amplitude operators and inside the interface. In particular, these eq.s contain on the right hand side of and both self-coupling and cross-coupling terms. The former basically represent the propagation of each field mode in the presence of the corresponding coupling beam, as for a typical Λ-configuration supporting electromagnetically induced transparency18. The latter terms originate instead from the interaction between the far-detuned and the nearly resonant field mode (Cf. Fig. 1). Solutions of these coupled eq.s yield and ; upon converting back to the time-domain the resulting amplitude operators and can be rewritten in terms of the corresponding free-space operators and as,

Similar operators transformation (4) have been used in investigations of quantum optical properties of parametric processes in atomic media such as amplification enhancement19, mirrorless oscilations20, quantum noise and correlations in wave mixing21, efficient single-photon frequency switching and entangled state generation15, just to mention a few.

Here we use instead (4) to discuss a phase-resonant mechanism to control and especially to preserve the frequency-bin entangled state (1) through the interface of Fig. 1. It should be noted that in general the propagation of one field excitation that is shared between two atomic frequency transitions naturally tends to contaminate the quality of the entanglement. Two frequency modes sufficiently separated from one another may exhibit in fact appreciably different dispersion and absorption. In addition, the two coupling beams, each separately coupled to the two frequency components of the single-photon, naturally triggers a mode mixing which further spoils entanglement.

Results

The four complex amplitudes 's in (4) determine the evolution of the photon's electric field through the interface. The evolution depends, in particular, on the lasers initial relative phase Δϕc as expected for a closed-loop excitation structure where the two modes interact through a common spin-coherence. Each amplitude's expression is rather involved, yet for nearly resonant Raman transitions ( and ) and in the limit of Raman detunings for which , the overall space-dependence of can be rewritten (δcp = 0, δcm = Δ) as a superposition of two waves,

and similarly for

where the detuning and space dependences have been conveniently omitted on purpuse. We denote by

and

the complex refractive index exhibited by the atomic interface respectively on the nearly-resonant transition and on the far-detuned Raman transition (See Fig. 1). The remaining matrix terms and in (4) can be shown to obtain respectively from and upon a suitable replacing of ωp → ωm and .

The evolution of the frequency-bin entanglement, on the other hand, is studied by seeking the conditions under which the initial state (1) maintains the form,

with the entanglement clearly being preserved when the two amplitudes in (9) remain equal to those in (1). The evolution hinges on the space-time dependence of the complex amplitudes ap(z, t) and am(z, t) and this is what we now compute. The square magnitude |ap(z, t)|2 represents the normal-ordered averaged Poynting vector Sp(z, t) = 〈Φe|:Sp(z, t):|Φe〉 in the mode p across the interface, scaled to the single-photon incident pulse peak power density So. Similarly for |am(z, t)|2. The field correlators required to obtain Sm(z, t) and Sp(z, t)22 are computed using the fact that at some given reference time (t) across an interface the expectation values are independent of the representation. For a single-photon wavepacket of length and with a Gaussian frequency distribution one obtains after some lengthily algebra,

where the upper and lower signs denote specifically So × |am(z, t)|2 and So × |ap(z, t)|2. Evolution of the entanglement hinges on the interference of the two envelopes,

and

These are modulated Gaussians propagating at different group velocities , damping over different length scales and subject, in addition, to an important (out-of-phase) modulation with a phase .

Interference can easily be controlled both through this external phase and through the internal optical response of the atoms, respectively, through the couplings relative phase (Δϕc) and through the real (η±) and imaginary (κ±) parts of n± in (7–8). The medium response controls, in particular, the phase of the interference term in (10), responsible for photon swapping between the two modes.

We first illustrate a situation, a main point in our proposal, where the interface can be tuned to avoid degradation of the state (1). The frequency-bin entangled state (1) remains largely unspoiled, in fact, for a vanishing (pulse) detuning δp and for coupling beams relative phases such that Δϕc − ϕη = 2n × π, as shown in Fig.s 2a. This corresponds to a phase Φ for which in (10). Physically, this arises from the matching of dark states and can be understood supposing that each component of the entangled state creates its own dark state through the corresponding coupling beam. When the two dark states exactly match to one another the atoms will loosely couple to the two field modes leading to a regime of reduced absorption and slow-light propagation (Fig. 2a). For coupling beams of the same intensities this occurs23 for a photon Rabi frequencies such that Ωp = Ωm and under the (four-photon) resonance condition ωm − ωcm = ωp − ωcp, both clearly met here. Within such a regime the entangled wavepacket can be delayed up to nearly 5 times the temporal width (τ) with negligible losses over a 500 μm long interface. This amounts to fractional delays - the ratio between the absolute delay and the pulse width τ - of the order of 5 occurring with very modest absorption and pulse deformation. Dark-state matching (Fig. 2a) sets an upper bound on the actual capability to perform reversible mapping24 of the entangled state (1). Conversely, when Δϕc − ϕη = (2n + 1) × π the other amplitude in (9), atoms will now couple to the photon field making both modes to quickly dissipate through the sample (Fig. 2b).

Figure 2
figure 2

Entanglement evolution.

Power density distribution from (10) yielding the evolution of the single-photon frequency-bin entangled state (1) through a 87Rb MOT trap of length L = 1000 μm and density N/V = 5 × 1013 cm−3 (See interface Fig. 1). The single-photon wavepacket has a τ = 5.2 μsec long Gaussian envelope with a detuning δp = 0 and a mode separation Δ = 20 × γ2 while the Rabi frequency of the coupling beams is Ωc = 2 × γ2. Clockwise from (a) → (d) the relative phase Δϕc − ϕη takes respectively the values {0, π, π/2, π/2}. Slow evolution takes place with little absorption preserving the state (a), with quite strong damping (b) or through damped coherent spatial oscillations between mode p (c) and mode m (d). The wavepacket evolution occurs with an overall velocity (orange dashed) (a), (b) and (c, d). Color dots in (c,d) depict the wavepacket drift due to absorption. Note the different length scales in Fig. 2a and Fig. 2(c, d).

Full size image

We also include in the discussion a somewhat opposite situation in which the entanglement is largely spoiled. That occurs for coupling phases Δϕc such that Δϕc − ϕη = (2n + 1) × (π/2) and δp = 0, as shown in Fig.s 2(c, d). The resulting space–time evolution of the entangled state (9) exhibits spatial oscillations between its two frequency components with a significant damping over much shorter lengths, as we may see by comparing Fig. 2a and Fig.s 2(c, d). Such a characteristic coherent photon swapping between the two-frequency bins arises from maximum interference of the two envelopes and in (10). In spite of the different spreading of these two envelopes, the entangled state wavepacket evolves at a velocity that locks at , as it may be directly inferred from the composition of the slow () and fast () velocities components in (10). Actual departures of the photon wavepacket overall evolution from υ are due to increasing values of the absorption with distance. Notice that only few times can entanglement be recovered over a typical 100 μm length scale. As inferred from (7–8) and (10), this occurs almost periodically at specific points spaced by . By varying Losc, modifying for instance the atomic response through the pulse detuning δp (see eq.s 7–8), one may in principle adjust the position where entanglement is retained15, though this is clearly not practical. For the realistic interface parameters of Fig. 2, a sizable level of decoherence due to losses seems to further prevent such a depth-dependent entanglement from maintaining the original state (1).

The three different damping situations are detailed in Fig. 3, where we plot the spatial damping of the maximum degree of entanglement. Notice that preserving the entanglement is rather sensitive to the pulse detuning δp from resonance (dashed).

Figure 3
figure 3

Maximum entanglement distribution.

Frequency-bin entangled state peak power density spatial distribution in units of So for the evolution profiles of Fig. 2. Each curve is plotted at a specific time tmax obtained from the ratio of the position z and each of the evolution overall velocities shown Fig. 2 (orange dashed). Green curves describe the weak damping case of Fig. 2a respectively for δp = 0 (solid) and δp = 0.1 × γ2 (dashed). Red curve (dot – dashed) describes the strong damping case of Fig. 2b, while blue and purple curves correspond to the two frequency-mode swapping intensity distribution of Fig. 2(c, d).

Full size image

Discussion

The present phase-resonant atomic interface mechanism requires narrowband single-photon states. Spontaneous parametric downconversion may be a suitable candidate for the generation of the state |Φe〉 in (1). Alternatively, two concomitant spontaneous Raman scattering processes may be used, namely by pumping the atomic ensemble with two pump beams of different frequencies and a fixed phase relation between them. Raman scattering is responsible for the emission of idler (Stokes) and signal (anti-Stokes) twin photons with positive and negative frequency shifts, relative to the two pumps. In the presence of only one pump, the observation of a photon in the idler mode would herald the emission of a signal photon with a well defined frequency, determined by the pump frequency as demonstrated in25. In our case, however, in which both pumps are present, the above emission process will occur through either pump with low but nearly equal probabilities, hence the observation of an idler photon heralds the emission of a signal single-photon. The probability of both processes occurring simultaneously is negligible for sufficiently weak coupling beams. However, the detection of the single idler photon does not reveal, even in principle, which pump has triggered the emission of the photon in the signal channel. Such an indistinguishability clearly results in the generation of the superposition state (1). The phase ϕη of state (1) is determined by the relative phase between the two coupling beams and can be easily adjusted to have the desired value. Such an initial phase can also be fully characterized with homodyne tomography (See e.g.13,26), prior propagation through the interface.

The main advantages of the analytical approach adopted in solving the coupled evolution eq.s (2–3) are the physical insight into the nature of a new control mechanism for a frequency-quibit and the ease in computing all different aspects of its evolution (see e.g. Fig.s 2a–2d). Following eq. (10), in fact, control of the frequency-bin entangled state hinges on the interference of the two modulated Gaussians envelopes and and is attained by manipulating both the internal optical response of the atoms and the (external) coupling relative phase Δϕc. Loss of entanglement due to absorption, dispersion and mixing intrinsic to the resonant excitation of the interface's double-lambda configuration of Fig. 1 is all embedded in the joint space-time evolution of and .

Notice that the evolution of the frequency-bin entangled state is in general determined not only by the magnitude of the complex amplitudes ap(z, t) and am(z, t) but also by their relative phase. Only in the relevant situation of Fig. 2a, can such a relative phase be shown to remain essentially constant during propagation, at variance with the situation of Fig. 2(c, d) where the two mode components accumulate steep variations of the relative phase during propagation. This further complicates the possibility of achieving depth-dependent entanglement of two Fock-states15.

Although the present analysis has been carried out for the single-photon entangled state (1) control interface, the transformation (4) may also be directly used to study the case of a two-photon entangled state - with results that can be derived in a similar way - or to study extensions to control multi-photons entanglement. Extensions to control of a multi-frequency entangled state may also be conceived. In this case the frequency domain can be divided into several frequency bins, corresponding to different atomic transitions, where quantum information can be encoded. The interface mechanism would become an efficient control tool for multi-frequency entanglement in quantum memories based on atomic ensembles. To this extent, it should be noted that reversible mapping of multi frequency-entanglement24 would require coherence times which are largely independent of the number of (frequency) modes. This is at variance e.g. with recent schemes for time-bin multimode entanglement26,27 that are bound to work with a restricted number of time-bins. It is finally worth to emphasize that our scheme is rather general, in terms of the underlying working mechanism, though the above analysis specifically relates to a cold atoms interface30. It may well be adapted to other interfaces including atomic ensembles in solids such as e.g. crystals doped with rare-earth-metal ions28 or with N-V color centers29, both having a potential for developing quantum information architectures based on solid devices. Dark-state matching, in particular, is expected to remain robust providing a mean to compensate for differential dispersion and absorption also in these crystals.