Introduction

Quantum teleportation is the best known example of how entanglement serves as a valuable resource for information processing. Since the original discovery of quantum teleportation by Bennett et al. in 19931, remarkable technological advances have been made and teleportation with higher than classically achievable fidelities has been demonstrated experimentally2,3,4,5,6,7 up to the distance of 143 km8. In practice, perfect teleportation is not possible since, instead of maximally entangled states, decoherence effects force us to deal with mixed states. It has been shown that with classical communication and local operations perfect teleportation with mixed states is impossible1,9 and therefore, one of the current major challenges in accomplishing teleportation over long distances is to overcome the limitations imposed by decoherence and the subsequent mixedness of the resource state.

When an open quantum system, due to its coupling with the external environment, continuously loses information to its surroundings, the noise induced dynamics is called Markovian10,11,12. Non-Markovian quantum dynamics with memory effects arise when the system does not only lose information, but temporarily recovers some of it from the environment at a later time13,14. Recently, a significant progress in developing a general theory of non-Markovian quantum dynamics13,14,15,16,17,18,19,20 as well as in the experimental detection and control of memory effects21,22,23 has been made.

Previously, environment-assisted quantum processes have been studied in the context of e.g. quantum transport24,25 and communication networks26, but protocols for quantum information tasks utilising the non-Markovian nature of otherwise harmful noise have been so far missing. In this paper we show how quantum memory effects can be harnessed to give an advantage in mixed state quantum teleportation in the presence of dephasing noise. We consider photonics realisations due to their dominant role in the experimental implementations of teleportation8. The key element of the scheme introduced here are nonlocal memory effects where the local exposure of the bipartite quantum system to Markovian noise can create strong global memory effects27; a scheme which has also been recently experimentally demonstrated23. The fundamental source for these effects are the initial correlations between the local environments of the bipartite open system. For entangled photon polarisation states, nonlocal memory effects needed for the protocol arise naturally since the frequency distributions of the photons, which act as environments, are unavoidably correlated after a downconversion process23. We also analyse how the amount of initial correlations between the environments affects the fidelity of the teleportation and find that even in the absence of maximal correlations between the environments, the protocol will substantially outdo the performance of the known optimal protocol without memory effects9.

In the standard quantum teleportation protocol Alice has a qubit whose state |ϕ〉1 = α |+〉 + β |−〉 she wants to teleport to Bob. Alice and Bob share an entangled pair of qubits 2 and 3 in the Bell-state:

Alice performs a Bell-state measurement on the particles 1 and 2, which projects particle 3 in Bob's hands into one of four states depending on which Bell-state Alice gains as an outcome. Alice further communicates her measurement outcome to Bob who performs a unitary operation on particle 3 depending on the outcome of Alice. The final state of particle 3 is the original state |ϕ〉3 = α |+〉 + β |−〉. During the Bell-state measurement particle 1 becomes entangled with particle 2 and the state |ϕ〉1 is destroyed on Alice's side during the protocol.

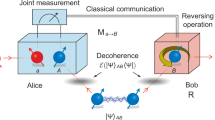
However, if the entangled pair of particles that Alice and Bob share is disturbed by noise, the fidelity of the standard teleportation goes down radically. Even if one chooses, instead of the standard teleportation scheme, an optimised protocol, perfect teleportation can no longer be achieved9. Let us now demonstrate how perfect teleportation can be achieved with photon polarisation states, even in the presence of dephasing noise, if the pair shared by Alice and Bob is influenced by nonlocal memory effects, see Fig. 1.

Figure 1
figure 1

A schematic picture of the teleportation protocol with nonlocal memory effects.

EPR refers to a source producing states of the form of equation (1) and BSM refers to a Bell-state measurement. The local noise before the BSM makes the EPR pair mixed while the noise in the last step of the protocol allows to recover the teleported state.

Full size image

Results

Let us assume that the pair of entangled photons is created in a spontaneous parametric downconversion process after which the two particles are sent to remote locations to Alice and Bob. However, the particle sent to Alice is not perfectly isolated, but is interacting with its local environment giving rise to local decoherence, which destroys the entanglement between the two parties. As a physical implementation of the local dephasing noise, we consider photon traveling through a quartz plate, where the polarisation degree of freedom (system) and the frequency degree of freedom (environment) interact22,23,27. The quartz plate exposes the polarisation state of the photon to a random external field giving rise to a dephasing evolution28.

Now, Alice wishes to teleport the state |ϕ〉1 = α |H〉 + β |V〉 to Bob. Here, H (V) refers to horizontal (vertical) polarisation state of the photon. Initially Alice and Bob share the Bell-state and the total initial state (system and environment) of the photons 2 and 3 is

where g(ω2, ω3) gives the joint frequency amplitude of the photons 2 and 3 and ∫ dω2dω3|g(ω2, ω3)|2 = 1. The Hamiltonian for the local dephasing due to the quartz plate takes the form

where, e.g., |V〉 ⊗ |ωi〉 denotes the state of photon i (i = 2, 3) with polarisation V and frequency ωi and () is the index of refraction for polarisation component H (V). The time dependent interaction Hamiltonian describing the evolution of the two-photon state is given by

where

and denotes the time photon i enters the quartz plate and the time photon i exits the quartz plate. Now the time evolution of the total system is given by . Let us also write .

In terms of our protocol, first photon 2 interacts with its quartz plate followed by the Bell-state measurement on photons 1 and 2. Then Alice communicates her measurement outcome to Bob and the interaction of photon 3 with its local environment in Bob's side finishes the procedure. The combined polarisation state of the systems 2 and 3, after photon 2 has interacted with its quartz plate on Alice's side, is

where the decoherence function κ2 is

is the birefringence and t2 the interaction time of photon 2. Now, if Alice and Bob were to perform the standard teleportation with the shared state ρ23(t2), the fidelity of the teleportation would decrease linearly with respect to κ2, see Fig. 2. Let us now describe how they can outperform this fidelity with nonlocal memory effects.

Figure 2
figure 2

The fidelities of the standard, optimal and non-Markovian protocols.

The fidelities of different teleportation protocols for the mixed state of equation (6) as a function of the decoherence function |κ2|. The red dashed line represents the fidelity of the standard protocol [equation (20)], the red dot dashed line the fidelity of the optimal protocol Fopt [equation (21)], the red solid lines the fidelity of the protocol with memory effects with δK ∈ [0, 0.1] [equation (19)] and the light red solid lines with δK ∈ [0.1, 0.5].

Full size image

After the local interaction of photon 2 the total state for the three photons is

where

This can be written in the form

where

are the Bell states. Alice then performs the Bell state measurement and communicates her results to Bob. Bob further applies a unitary operation on his particle depending on Alice's measurement outcome. Thus, so far, Alice and Bob have performed the standard teleportation scheme with the mixed state of equation (6). Now, in order to improve the protocol, Bob needs to harness the nonlocal memory effects. He can use the information sent by Alice and subject his particle to conditional noise depending on Alice's measurement outcome. By adding the conditional noise to his system, Bob actually cancels out the effect of the noise which earlier acted on Alice's system. He chooses the following unitary operations and the birefringence of his quartz plate to produce noise according to Alice's outcomes:

Let us assume that Alice's outcome of the Bell measurement is the state |ϕ+〉12. Now the total state of Bob's photon 3 is

where

and . When Bob subjects his photon to noise by putting his photon through a quartz plate with Δn3 = Δn2 his final state can be written as

where the decoherence function is

and t3 is the interaction time in Bob's quartz plate.

In the description of the downconversion process, the frequency distribution can be taken to be a joint Gaussian distribution23,27

where C = (Cij) is the covariance matrix with elements Cij = 〈ωiωj〉 − 〈ωi〉 〈ωj〉. We assume that both the means and the variances of ω2 and ω3 are equal, i.e., 〈ω2〉 = 〈ω3〉 = ω0/2 and . To quantify the frequency correlations we use the correlation coefficient satisfying |K| ≤ 1.

If Bob chooses t3 = t2 and the frequency distribution is of the form of equation (17) with the correlation coefficient K = −1, the polarisation state of photon 3 is given by equation (15) with , i.e., the magnitude of the decoherence function has returned to its original value equal to 1. If Bob now performs a phase gate with phase −ω0Δn2t2, perfect teleportation has been completed. The other measurement outcomes of Alice give the same result if Bob applies the operations given in equation (12). It is important to notice that all the steps of this protocol can be applied locally and that the applied noise is locally Markovian and globally non-Markovian within the bipartite system27.

Discussion

We have demonstrated how Alice and Bob can recover perfect teleportation in the presence of dephasing noise if Bob after the standard teleportation protocol subjects his particle to noise. The key element in the protocol are the nonlocal memory effects which arise when the local decoherence is present on Bob's side. The source of the nonlocal memory effects lies in the initial correlations between the local environments described by the correlation coefficient K, which in turn is determined by the width of the original pump pulse in the downconversion process. In the case of perfect anticorrelation K = −1 (delta peak pump), perfect teleportation is achieved and for an uncorrelated distribution K = 0 no advantage with respect to the standard protocol can be gained. It is also important to note that no initial entanglement is necessary between the local environments, but classical correlations suffice23,27.

Thus, we have shown that when the initial joint frequency distribution has perfect anticorrelation K = −1, this leads to perfect teleportation with mixed polarisation states. If, however, the initial pump pulse does not have a delta peak distribution, the fidelity of the protocol decreases. In the following we study how a finite width of the pump pulse will affect the fidelity of the teleportation protocol. Let us take the correlation coefficient to be K = −1 + δK, i.e., δK measures the deviation from the ideal case. The fidelity F = 1〈ϕ| ρ3 |ϕ〉1 between the original state α |H〉 + β |V〉 and the teleported state becomes

Considering the worst case scenario, i.e. |α|2 = |β|2 = 1/2, we obtain

If the teleportation was performed with the decohered state in equation (6), using the standard scheme without taking advantage of the memory effects, we would have the fidelity

If instead of the standard teleportation scheme, one would use an optimal teleportation scheme for the decohered state at hand9, one would get the fidelity

which gives the value 2/3 for a classical state. The fidelities of the different teleportation protocols are plotted in Fig. 2 as a function of the decoherence function |κ2(t2)|. We see that the fidelity of the protocol with memory effects for sufficiently large values of the correlation coefficient |K| is still much larger than the fidelity of the standard protocol or the optimal protocol in the absence of memory effects. For sufficiently large correlations (δK ≤ 0.1, i.e. −1.0 ≤ K ≤ −0.9) the fidelity of the protocol with memory effects exceeds the fidelity of the optimal protocol without memory effects all the way to an almost fully decohered state. For a smaller value of correlations (0.1 ≤ δK ≤ 0.5) the fidelity still exceeds the one of the standard protocol. It is also important to note that the high value of the correlation coefficient K = −0.9 (or δK = 0.1) is experimentally realisable23.

In Fig. 3, we plot the fidelity of the proposed protocol as a function of the non-Markovianity measure introduced in13. Assuming t3 = t2, and , the dynamical map describing the teleportation protocol for Alice's initial unknown state |ϕ〉 = α |H〉 + β |V〉 can be written as

Here, ρF is given by Eq. (15), ρF(t, 0) denotes the case where the teleportation is performed at time t with no quartz plate on Bob's side and ρF(t2, t − t2) the case of teleportation at time t2 with subsequent evolution with Bob's quartz plate. The non-Markovianity measure can now be written analytically23:

Thus, the fidelity of the protocol in equation (19) as a function of the non-Markovianity is

As can be seen in Fig. 3, the fidelity is a monotonically increasing function of the non-Markovianity and thus the memory effects act as a resource for quantum teleportation.

Figure 3
figure 3

The fidelity of the proposed protocol as a function of the non-Markovianity measure .

In the inset the different values of the decoherence function |κ2(t2)| are given.

Full size image

Summarising, we have found that nonlocal memory effects can substantially increase the fidelity of mixed state quantum teleportation in the presence of dephasing noise. In the protocol Alice and Bob act on their particles locally and the nonlocal memory effects occur due to initial correlations between the local environments of the photons. In order for Bob to harness the memory effects, he needs to subject his photon to local noise after the standard teleportation protocol. We have shown that one can perform perfect mixed state teleportation of photon polarisation states if the environments of the two photons share maximal initial correlations. The protocol presented here demonstrates how to overcome dephasing noise induced by random external fields in a quantum communication setup by exploiting memory effects. The result serves as an encouraging example of how non-Markovianity can serve as a resource for quantum information tasks but it still remains to be shown whether the same technique could be applied for environments giving rise to also relaxation and dissipation.