Introduction

A rapid processor and reliable memory are indispensable components for building quantum computers. Recent progress in mesoscopic objects, e.g., superconducting qubits, shows that this kind of artificial systems can couple strongly to electromagnetic field and enable fast quantum logic gates1. However, they possess relatively short coherence time. On the other hand, microscopic systems, e.g., nitrogen-vacancy (NV) centers in diamond2, naturally have rather long coherence time. Therefore, it is attractive to combine the two types of systems by employing their hybrid architecture3. In order to take the advantages of both, quantum state transfer (QST) between the two sides is crucial. To this end, some strategies have been proposed with hybrid systems4,5,6,7,8,9,10, where a superconducting qubit acts as a processing unit and the other ones serve as memory units.

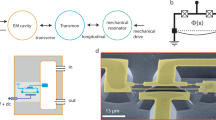
There are generally two kinds of hybridity: coupling the two elements via a quantum bus7 or directly8. First, a superconducting qubit can be coherently coupled to an ensemble of NV centers in a diamond via a superconducting transmission-line resonator, which acts as a quantum bus6,7. However, the NV center ensemble usually has relatively much shorter coherence time comparing with single NV center and the coupling of single NV center to the transmission-line resonator is too weak to be usable, usually under 0.1 kHz7. Meanwhile, a superconducting flux qubit can be directly coupled to an NV center with a coupling strength on the order of 10 kHZ8,9,10. But, such schemes are difficult to extend to couple long distance qubits as the superconducting qubit can not be too large. Therefore, to be potentially extended to quantum networks11, many QST schemes have been investigated in systems consisting of two coupled resonators12,13,14,15,16,17,18,19,20,21. Typically, an NV center and a superconducting qubit can be coupled to a nanomechanical resonator22,23,24 and a transmission-line resonator1, respectively. On the other hand, the two different resonators can be parametrically coupled to form an electromechanical architecture25. With rapid experimental progress25,26,27,28, this typical system can have many potential applications for hybrid quantum information processing16,17,18 and entanglement29,30,31.

In this paper, we propose a scheme to realize high fidelity QST between a superconducting qubit and an NV center, which provides the possibility of storing a state of a superconducting qubit into the spin-based quantum memory via the electromechanical system. Previous works in similar coupled resonator systems, such as Refs. 17, 18, 19, 20, 21, were mainly focusing on the large inter-resonator coupling regime (we will specify different regimes later), where analytical result can be obtained21. However, after taking the decoherence effects into consideration, we investigate the QST dynamics numerically and find that both the small and large coupling regimes of this system can not support high fidelity QST with current technology. The main result of present work is the comprehensive study of QST in the intermediate coupling regime, which is lacking in previous studies17,18,19,20,21. Our motivation also relies on the fact that the intermediate coupling regime can be realized more easily as it requires smaller inter-resonator coupling comparing with large coupling regime and thus our result is useful and can be tested in a near future experiment. Interestingly, the main finding here is that fast and high fidelity QST is possible in the intermediate coupling regime, even better than that of the large coupling regime. The physics behind this surprising result is that the decoherene has less effect in the intermediate coupling regime since the time of QST is shorter than that of both the small and large coupling regimes. Therefore, our result provides a promising route towards high fidelity QST in similar systems with coupled resonators.

Results

The hybrid system

The hybrid system consists of a superconducting qubit (NV center) coupled to a transmission-line (nanomechanical) resonator and the two resonators are parametrically coupled. Our final goal is to transfer the quantum state of a superconducting qubit, the processor, to the NV center, the quantum memory, via the two coupled resonators. Since the QST process interchanges the information between the two subsystems, the main results we obtained in the following should also be valid for the reverse transfer, i.e., transfer the state of the NV center to the superconducting qubit. For convenience, hereafter, the subscript 1(2) stands for the superconducting qubit (NV center) and a(b) for the transmission-line (nanomechanical) resonator, respectively. A superconducting qubit can be treated as a two-level system and the transmission-line resonator can be modeled as a single Bosonic mode32,33: Ha = ωaa†a, where we assume hereafter, ωa and a (a†) are the mode frequency and the annihilation (creation) operator of the resonator, respectively. The superconducting qubit can be capacitively coupled to the transmission-line resonator and the interaction Hamiltonian can be written as32,33

where σ± = (σx ± iσy)/2 are the raising/lowering operators of the superconducting qubit and the coupling strength g1 can be tuned by an external magnetic flux of the qubit loop32,33.

Meanwhile, the ground state of a negatively charged NV center is spin triplet ms = 0 and ms = ±1 and there is a zero-field splitting between them due to spin-spin interaction. The two states | ± 1〉 are coupled to the |0〉 state by different polarized driven fields with the same detuning Δ > 0 and strength Ω34. In a frame rotating with the driven frequencies, the Hamiltonian of the NV center can be written as

which couples |0〉 to the bright state , while leaves the dark state uncoupled. The eigenstates of the NV center are |d〉, |m〉 = cos ϑ|0〉 − sin ϑ|b〉 and |e〉 = cos ϑ|b〉 + sin ϑ|0〉 with and the corresponding eigenvalues are labeled as ωd,m,e. The Hamiltonian of a nanomechanical resonator can be written as Hb = ωbb†b with ωb and b (b†) being the mode frequency and the annihilation (creation) operator of the nanomechanical resonator, respectively. A magnetic tip is attached to the nanomechanical resonator at a distance h ~ 25 nm above a NV center and thus creates a strong coupling between the two elements. The mechanical resonator can be a doubly clamped beam or a cantilever and the magnetic tip can be attached at the position of an antinode and the unclamped end, respectively. The superconducting qubit is far away from the tip (comparing with h) and thus feels negligible magnetic field. When ωb = ωdm = ωd − ωm, the interaction between the NV center and the nanomechanical resonator reads22

where , and is the coupling strength.

Furthermore, we consider a capacitive coupling between the microwave transmission-line and the nanomechanical resonator25,28. The mechanical resonator is driven by an ac voltage, which matches the energy difference between the electrical and mechanical systems and thus couples the two. Then, an effective linear coupling between the two resonators can be induced and the effective electromechanical interaction Hamiltonian can be written as

where the coupling strength J determines the speed of the energy transfer between the two resonators. The nanomechanical resonator here can be a doubly clamped beam28 or a metallic membrane25. However, the direct capacitive coupling strength of the microwave resonator and the mechanical beam is usually very small in typical experiment28. Fortunately, one can replace the coupling capacitor by a superconducting qubit, which can greatly enhance the coupling strength35. Alternatively, one can use a metallic membrane to serve as one of the two parallel metal plates of the coupling capacitor25, where one can readily obtain J ~ g2. In this case, the coupling between the membrane and the NV center can be induced by strain36, where strong coupling can be achieved. Therefore, the total Hamiltonian for the hybrid system is given as

The competition of different couplings of this Hamiltonian will yield three coupling regimes. As J determines the time scale of the systematic dynamics, we will call , and J ~ g1 ~ g2 as large, small and intermediate (inter-resonator) coupling regime, respectively. In addition, to get coherent dynamics, the coupled systems described in Hamiltonian in Eqs. (1) and (2) need also to be operated in the strong coupling regime.

The quantum state transfer

We now study the QST from a superconducting qubit to a NV center. We consider the zero- and one-excitation subspaces, i.e., spanned by the basis of {|0m〉12|10〉ab, |0m〉12|01〉ab, |1m〉12|00〉ab, |0d〉12|00〉ab}. The basis vectors and their corresponding populations are labeled as |φn〉 and Pn (n = 1, 2, 3, 4), respectively. For an initial state |ψ〉i = |ψ1〉|m〉2|00〉ab with |ψ1〉 = cos θ|1〉1 + sin θ|0〉1, the goal of the QST is to obtain a final state of |ψ〉f = |0〉1(cos θ|d〉2 + sin θ|m〉2)|00〉ab. Note that |0〉1|m〉2|00〉ab will not evolve under the act of Hamiltonian (4) and the QST completes when the excitation initially in the superconducting qubit (P3 = 1) transfers to the NV center (P4). We estimate the performance of our scheme by the conditional fidelity defined by F = 〈ψ1|ρa|ψ1〉, with ρa being the reduced density matrix of the NV center from the final state, under decoherence rates ξ using the Lindblad master equation, see the method section for details.

The small coupling regime

In this regime, the dynamics can be understood as two weak coupled subsystems with each having a Jaynes-Cummings type interaction. The dynamics of the system is characterized by a fast oscillation behavior with frequency g = g1 = g2 accompanied by a slow oscillation envelope with frequency J/2. Choosing θ = π/4, the fidelities are plotted in Fig. 1 with different ξ. This transfer is completed at instants Tw = (2k + 1)π/J with k being a nonnegative integer. However, the maximum fidelity with ξ = 0.03 is less than 70%. The relatively large infidelity is mainly due to the decoherence effect since the transfer time is very long because of the very small J. To obtain a fidelity about 95%, one needs to reduce the decay rates to ξ/10, which is very challenging. Moreover, it is worth to note that if the symmetric coupling situation g1 = g2 is not satisfied, the deviation brings detrimental influence to the QST: the population maximum will decrease rapidly with the increase of the deviation denoted by |g2 − g1|/g2. Furthermore, the fidelity is too small, which means it is impossible for QST with asymmetric coupling in this regime.

Figure 1
figure 1

Fidelity as a function of the reduced time of t/(2π) in the small coupling regime with J = 0.1 for different ξ, other parameters are θ = π/4, ζ = 0.001 and g1 = g2 = 1.

Full size image

The large coupling regime

In this regime, the system can be considered as two subsystems connected by large photon hopping. The relatively large coupling between the two resonators services as a fast channel to transfer the energy residing in the two qubits. The system dynamics can be characterized by two distinct oscillating frequencies, fast oscillation with frequency J and slow oscillation with frequency21g2/J. QST can be completed at instants Ts = (k + 1/2)πJ/g2 with k being a nonnegative integer. The performance of this regime is better than that of the small coupling regime, as shown in Fig. 2(a). The maximum fidelity of the transfer process is about 75% for present experimental parameter of ξ = 0.03. To obtain a fidelity above 90% and 95%, one needs to reduce the decay of the system to ξ/3 and ξ/10, respectively. In this regime, as shown in Fig. 2(b), asymmetric coupling strength will introduce little influence and thus it is more robust against coupling strength deviation than that of the small coupling regime. With the increase (decrease) of g1 from the symmetric value of 1, the transfer time will be shortened (prolonged) and the fidelity of the QST will be gradually increased (decreased).

Figure 2
figure 2

Fidelity as a function of the reduced time of t/(2π) in the large coupling regime with J = 10, other parameters are θ = π/4 and ζ = 0.001.

(a) For g1 = g2 = 1 with different ξ. (b) For g2 = 1 and ξ = 0.03 with different g1.

Full size image

The intermediate coupling regime

In the following, we will focus on the QST performance in the intermediate coupling regime, which is the best choice for QST purpose. First, the QST in the small coupling regime needs very long time () and thus decoherence will introduce huge errors. Second, the interaction between the resonators is usually weak, or at least is the same order as the qubit-resonator interaction g. Though we may tune g to match the condition of , i.e., the large coupling regime, the expense is that the effective coupling will be decreased and the time to complete the QST will also be relatively long: . This means that the time needed for QST in the two regimes are much longer than their respective time scale of 1/g and thus decoherence will cause intolerable influence in both regimes. However, for the intermediate coupling regime J ~ g, as the time needed for QST will be Ti ~ 1/J ~ 1/g, we expect higher fidelity QST than that in the two other regimes.

For verification purpose, we plot the fidelity of the QST process in Fig. 3(a) with g2 = g1 = 1, ξ = 0.03 and 0.01 ≤ J ≤ 3. It is clear that the fidelity presents regular distribution in the whole region and each red spot corresponds to a maximum. When J increases gradually from 0.01 to 1.2, the red spot moves closer and closer to the vertical axis. When , the fidelity reaches a maximum value with the shortest QST time. If one continues to increase J towards J > 1.2, the red spot moves away from the vertical axis. It means that the time needed for QST will increase gradually and at the same time the fidelity will decease gradually. Comparing with that in the Fig. 1 and Fig. 2, the QST here completes in a much shorter time (the maximum value of the fidelity here move towards the vertical axis), which leads to the increase of QST efficiency and fidelity. Therefore, our numerical results show that the QST performance in the intermediate regime can be greatly enhanced comparing to that in the other two regimes. In order to have an insight into the detail population changes, we focus on the red spot closest to the vertical axis, the populations for different states are plotted in Fig. 3(b). The amplitude of P4 reaches the largest magnitude, implying the initial state fully transferred from the superconducting qubit to the NV center. Therefore, J ~ g makes the quantum bus to be a expressway and the excitation can pass through faster and with higher fidelity.

Figure 3
figure 3

Fidelity as a function of the reduced time of t/(2π) in the intermediate coupling regime with ξ = 0.03 and ζ = 0.001.

(a). For θ = π/4, g1 = g2 = 1 and J ∈ [0.01, 3]. (b). Time dependent populations with J = 1.2 in (a). (c) For θ = π/4, J = 1.2, g2 = 1 and g1 ∈ [0.01, 3]. (d). Maximum fidelity as a function of θ with g1 = g2 = 1 and J = 1.16.

Full size image

Furthermore, we investigate the influence of asymmetric coupling g2 ≠ g1 to the QST in this regime. Figure 3(c) shows the time-dependent population of the target state P4 with ξ = 0.03, g2 = 1, J = 1.2 and 0.01 ≤ g1 ≤ 3. One can easily find that the amplitude of P4 enhances and rapidly moves to the left when g2 increases gradually from 0.01. This improvement does not means the success of faithful QST, due to the additional influence by vertical adjacent peaks. However, within the small region of g1 = 1.1 ± 0.1, the peaks are relatively far apart from each other in vertical direction, which makes the higher fidelity QST to be realizable. We have confirmed that one can perfectly realize the QST with g1 = g2 = 1 and , where the QST needs less time (which is about 1/10 and 1/5 of the time in small and large coupling regimes, respectively) and the QST has the highest fidelity of 96%. We further investigate the θ dependence of the maximum fidelity, as shown in fig. 3(d), which indicates that the larger θ will lead to larger fidelity.

In conclusion, we have demonstrated that a high fidelity QST between a superconducting qubit and an NV center in diamond in a hybrid electromechanical system can be realized in the intermediate coupling region. We have numerically simulated the evolution of whole system and find that QST can be realized much faster and more reliable in the intermediate coupling regime than that in the small or large coupling regimes. As the above conclusion is model independent, our result may be directly extended to similar systems consisting of coupled resonators and thus provides a promising way for realizing high fidelity QST.

Methods

Modeling of decoherence effects

Inevitably, the QST process will suffer from decoherence. We simulate the performance of our scheme under realistic conditions by considering the decays of the two resonators (κa and κb), the relaxation (γ1 and γ2) and dephasing (Γ1 and Γ2) of the two qubits. Under these conditions, the whole system can be described by the Lindblad master equation

where is the Lindblad operator. We next justify our chosen parameters. The superconducting qubit in a transmission-line resonator can be protected by the resonator, for a planar transmon qubit, relaxation and coherence times of 44 and 20 μs are reported for a 1D resonator37, which leads to Γ1/2π = 8 kHz and γ1/2π = 3.5 kHz. The decay rate of the 1D transmission-line resonator is around (lifetime τa = 45 μs38). The coupling between the superconducting qubit and the transmission-line resonator is very strong and can be controlled very well and thus we assume g1 can be tuned to arbitrary value we want, which can be achieved by using a flux-biased rf SQUID to couple the superconducting qubit to the cavity39. For a temperature of T = 100 mK and the quality factor Q = 106, the decay rate of the nanomechanical resonator is 23 and 22. As the decay rates are in the same order Γ1 ~ γ1 ~ κb ~ κa, we treat them as a same parameter ξ = κa. Hereafter, all the parameters will be normalized in unit of g2 and thus ξ = 0.03. The energy relaxation and coherence times of the NV center can be very long comparing with others34 and thus γ2 and Γ2 is very small. Therefore, we have taken these two parameters as the same in the numerical simulations, i.e., Γ2 = γ2 = ζ = 0.001, which corresponds to a coherence time of only 1.4 ms.