Abstract
Constructed from Bai-Xu-Wang-class monogamy relations, multipartite entanglement indicators can detect the entanglement not stored in pairs of the focus particle and the other subset of particles. We investigate the k-partite entanglement indicators related to the αth power of entanglement of formation (αEoF) for k ≤ n, αϵ and n-qubit symmetric states. We then show that (1) The indicator based on αEoF is a monotonically increasing function of k. (2) When n is large enough, the indicator based on αEoF is a monotonically decreasing function of α and then the n-partite indicator based on
and n-qubit symmetric states. We then show that (1) The indicator based on αEoF is a monotonically increasing function of k. (2) When n is large enough, the indicator based on αEoF is a monotonically decreasing function of α and then the n-partite indicator based on  works best. However, the indicator based on 2 EoF works better when n is small enough.
works best. However, the indicator based on 2 EoF works better when n is small enough.
Similar content being viewed by others
Introduction
Quantum correlations that comprise and go beyond entanglement are not monogamous. Only entanglement can be strictly monogamous1, that is, they obey strong constraints on how they can be shared among multipartite systems. This is one of the most important properties for multipartite quantum systems2. So these monogamy relations can be used to characterize the entanglement structure in multipartite systems3 and concretely the difference between the left- and right-hand side of them can be defined as indicators to detect multipartite entanglement not stored in pairs of the focus particle (e.g., the first particle) and the other subset of particles4.
For the squared concurrence, the indicator named three-tangle3 can be used to detect genuine multipartite entanglement (which are entangled states being not decomposable into convex combinations of states separable across any partition) in three-qubit pure states. However, for three-qubit mixed states, there exist some entangled states that have neither two-qubit concurrence nor three-tangle5. To reveal this critical entanglement structure, some multipartite entanglement indicators based on Bai-Xu-Wang-class monogamy relations for the entanglement of formation (EoF) have been proposed4,6,7. In this paper, we will study which multipartite entanglement indicator for EoF works better. By “work better” we mean that is larger than the other8.
We resolve the above problem in the following ways. Firstly, we prove that the αth power of EoF (αEoF,  ) obeys a set of hierarchy k-partite
) obeys a set of hierarchy k-partite  monogamy relations of Eq. (10) in an arbitrary n-qubit state
monogamy relations of Eq. (10) in an arbitrary n-qubit state  . Here, the k-partition means the partition A1,
. Here, the k-partition means the partition A1,  , Ak−1 and
, Ak−1 and  . Based on these monogamy relations, a set of new multipartite entanglement indicators are presented correspondingly, which can work better than the 2 EoF-based indicators in n-qubit symmetric states. However, we find that the 2 EoF-based indicator can work better than the αEoF-based indicators for
. Based on these monogamy relations, a set of new multipartite entanglement indicators are presented correspondingly, which can work better than the 2 EoF-based indicators in n-qubit symmetric states. However, we find that the 2 EoF-based indicator can work better than the αEoF-based indicators for  when n is small enough (e.g., n ≤ 9).
when n is small enough (e.g., n ≤ 9).
Results
This section is organized as follows. In the first subsection, we review the monogamy relations for 2 EoF in n-qubit systems. We then prove in the second subsection that the αEoF obeys hierarchy k-partite monogamy relations for  and any n-qubit states. In the third subsection, we construct the entanglement indicators on n-qubit symmetric states and show their monotonic properties. Two examples are given in the forth subsection to verify these results.
and any n-qubit states. In the third subsection, we construct the entanglement indicators on n-qubit symmetric states and show their monotonic properties. Two examples are given in the forth subsection to verify these results.
Review of monogamy relations for EoF
Coffman, Kundu and Wootters3 proved the first monogamy relation for the squared concurrence in three-qubit states. Then, Osborne and Verstraete9 proved a set of hierarchy k-partite monogamy relations for the squared concurrence in n-qubit states  , which have the form
, which have the form

where A1 is the focus qubit,  ,
,  is the concurrence of
is the concurrence of  in the bipartition
in the bipartition  and
and  is a k-partite n-qubit state.
is a k-partite n-qubit state.
Based on these Osborne-Verstraete-class hierarchical monogamy relations in Eq. (1), a set of multipartite entanglement indicators can be constructed as follows

where the entanglement measure is the squared concurrence. These indicators can detect the entanglement not stored in pairs of A1 and any other k − 1 party (i.e., A2,  , Ak−1 and
, Ak−1 and  )4. However, there exists a special kind of entangled state10 which has zero entanglement indicator. Moreover, the calculation of multiqubit concurrence is extremely hard due to the convex roof extension. Therefore, it is natural to ask whether other monogamy relations beyond the squared concurrence exist.
)4. However, there exists a special kind of entangled state10 which has zero entanglement indicator. Moreover, the calculation of multiqubit concurrence is extremely hard due to the convex roof extension. Therefore, it is natural to ask whether other monogamy relations beyond the squared concurrence exist.
Recently, Bai et al.4 and Oliveira et al.11 respectively proved that 2 EoF is monogamous in n-qubit states, as follows

Moreover, Bai et al.6 exactly showed that there are a set of hierarchy k-partite monogamy relations for 2 EoF in an arbitrary n-qubit states, which obey the relation

Generally, Zhu and Fei7 proved that αEoF obeys the following monogamy relation in n-qubit states,

where  . (In fact, Eq. (5) obviously satisfies for α > 2 which can be obtained from Eq. (4) and ref. 12.)
. (In fact, Eq. (5) obviously satisfies for α > 2 which can be obtained from Eq. (4) and ref. 12.)
Because some bipartite multiqubit EoF of  can be calculated via quantum discord13,14, the entanglement indicator
can be calculated via quantum discord13,14, the entanglement indicator  from Eqs (3, 4, 5) can be obtained and can characterize multipartite entangled states in some n-qubit states4,6,7. In these entanglement indicators, how to choose a better indicator to detect that there exists multipartite entanglement is a problem. In the following subsections, we will try to resolve the problem.
from Eqs (3, 4, 5) can be obtained and can characterize multipartite entangled states in some n-qubit states4,6,7. In these entanglement indicators, how to choose a better indicator to detect that there exists multipartite entanglement is a problem. In the following subsections, we will try to resolve the problem.
Hierarchy k-partite monogamy relations for αEoF
In this subsection, we firstly summary of some existing conclusions and then get the hierarchy k-partite monogamy relations for αEoF.
As we know, EoF is a well defined measure of entanglement for bipartite states. For any two-qubit state ρAB, an analytical formula was given by Wootters15 as follows

where  is the concurrence with the decreasing nonnegative λi being the eigenvalues of the matrix
is the concurrence with the decreasing nonnegative λi being the eigenvalues of the matrix  . Here,
. Here,  and
and  is the binary Shannon entropy. Recently, Bai et al.6 proved that f(x) is a monotonic and concave function of x. Moreover, Zhu and Fei7 proved that f(x) satisfies the following relation
is the binary Shannon entropy. Recently, Bai et al.6 proved that f(x) is a monotonic and concave function of x. Moreover, Zhu and Fei7 proved that f(x) satisfies the following relation

where  , x and
, x and  . They also proved that EoF obeys the following relation
. They also proved that EoF obeys the following relation

for the bipartite quantum state  in
in  systems. Because a
systems. Because a  pure state
pure state  is equivalent to a two-qubit state under the Schmidt decomposition16, we have
is equivalent to a two-qubit state under the Schmidt decomposition16, we have

From Eqs (1) and (6, 7, 8, 9) for n-qubit systems, we can easily obtain that the following hierarchy k-partite monogamy relation holds.
Theorem 1 For any n-qubit state  , EoF satisfies the following monogamy relation
, EoF satisfies the following monogamy relation

where  and
and  .
.
The αEoF satisfies the hierarchy monogamy inequality (10) for any  , while the αth power of concurrence satisfies hierarchy monogamy inequalities for any α ≥ 29,12. This phenomenon shows a difference between the two kinds of entanglement measures. On the other hand, the inequality (10) is a generalization of Eq. (5) in ref. 6 and Eq. (19) in ref. 7. More specifically, Eq. (10) equals to Eq. (4) when α = 2 and is the same as Eq. (5) when k = n.
, while the αth power of concurrence satisfies hierarchy monogamy inequalities for any α ≥ 29,12. This phenomenon shows a difference between the two kinds of entanglement measures. On the other hand, the inequality (10) is a generalization of Eq. (5) in ref. 6 and Eq. (19) in ref. 7. More specifically, Eq. (10) equals to Eq. (4) when α = 2 and is the same as Eq. (5) when k = n.
Properties of hierarchy entanglement indicators
For any n-qubit state  and αEoF
and αEoF  , we can define a hierarchy entanglement indicator based on the corresponding monogamy relation in Eq. (10) as follows
, we can define a hierarchy entanglement indicator based on the corresponding monogamy relation in Eq. (10) as follows

where

It can be used to detect the entanglement for the k-partite case of an n-qubit system6 not stored in pairs of A1 and any other k − 1 party.
Here it should be noted that, different from the hierarchy entanglement indicator of the concurrence, the indicator of EoF depends on which qubit is chosen to be the focus qubit. Fortunately, the indicators of the concurrence and EoF are all focus-independent in symmetric quantum systems. In the following, we give some properties about the indicators of EoF only for n-qubit symmetric states.
Theorem 2 For any n-qubit symmetric state  , the hierarchy entanglement indicator satisfies
, the hierarchy entanglement indicator satisfies

and it is a monotonically increasing function of k, where  and
and  .
.
Proof. When  is a symmetric state, it is permutation invariant. Then,
is a symmetric state, it is permutation invariant. Then,  ,
,  and i ≠ j, we have
and i ≠ j, we have  and
and

Combining with Eq. (11), we have

Moreover, according to Eq. (5), we have

Then we can derive

where the inequality holds because of Eq. (16). Therefore, the entanglement indicator  is a monotonically increasing function of k.
is a monotonically increasing function of k.
In symmetrical quantum systems, the k-partite n-qubit monogamy relations of αEoF in Eq. (10) can be a monogamy equality (e.g., the corresponding results in the next subsection) and thus the corresponding entanglement indicator  can not work. However, we can choose an appropriate indicator
can not work. However, we can choose an appropriate indicator

to represent a better entanglement indicator which comes from the following result.
Theorem 3 For any n-qubit symmetric state  , the entanglement indicator obeys the following relation
, the entanglement indicator obeys the following relation

where  ,
,  and
and  . For any n, we have the following results
. For any n, we have the following results
-
1
When c = 0,
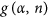 is a monotonically decreasing function of α.
is a monotonically decreasing function of α. -
2
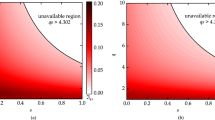
When c > 0 and b < 1,
 is a monotonically decreasing function of α if and only if
is a monotonically decreasing function of α if and only if

and  is a monotonically increasing function of α if and only if
is a monotonically increasing function of α if and only if

When c > 0 and b = 1,  is also a monotonically increasing function of α.
is also a monotonically increasing function of α.
Proof. From Eqs (10), (12) and (15), we have

According to the definition of b and c and the monogamy inequality (5), we get 0 ≤ c < b ≤ 1.
For any n, we will analytically prove the two necessary and sufficient conditions.
-
1
When c = 0, we have
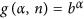 . Because 0 < b ≤ 1,
. Because 0 < b ≤ 1, 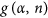 is a monotonically decreasing function of α.
is a monotonically decreasing function of α. -
2
When
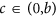 , we have
, we have

The monotonically decreasing property of  is satisfied if and only if the first-order partial derivative
is satisfied if and only if the first-order partial derivative  , which is equivalent to Eq. (20).
, which is equivalent to Eq. (20).
Furthermore, the monotonically increasing property of  is satisfied if and only if the first-order partial derivative
is satisfied if and only if the first-order partial derivative  , which is equivalent to Eq. (21).
, which is equivalent to Eq. (21).
From Theorem 3, we can obtain that the necessary and sufficient condition for the unit indicator is  and
and  . For any n-qubit symmetrical state, we can numerically compute the corresponding bounds to determine which is better,
. For any n-qubit symmetrical state, we can numerically compute the corresponding bounds to determine which is better,  indicator or the 2 EoF, as follows:
indicator or the 2 EoF, as follows:
After some deduction, we numerically obtain two bounds N1 and N2 with Eqs (20) and (21). When n ≥ N1, the  indicator is better than the 2 EoF indicator which comes from Eq. (20). The 2 EoF indicator is better than the
indicator is better than the 2 EoF indicator which comes from Eq. (20). The 2 EoF indicator is better than the  indicator when n ≤ N2, which comes from Eq. (21).
indicator when n ≤ N2, which comes from Eq. (21).
These results can be verified via two n-qubit symmetrical states in the next subsection.
Analytical examples
We will investigate the above results on permutationally invariant states, which are the W state, the superposition of the W state and the Greenberger-Horne-Zeilinger (GHZ) state of n qubits respectively.
For the W state
In this part, we analyze the n-qubit W state which has the form

For this quantum state, the n-partite n-qubit monogamy relations of αth power of concurrence as shown in ref. 7 are saturated and thus these concurrence-based entanglement indicators can not work. However, we will show that the αEoF-based indicator can be used to represent the entanglement in the n-partite n-qubit systems.
Using the symmetry of qubit permutations in the W state,  and
and  17, we have
17, we have

where  and
and  . This set of
. This set of  are positive since the αEoF is monogamous as shown in Eqs (5) and (10).
are positive since the αEoF is monogamous as shown in Eqs (5) and (10).
In order to study the properties of  , we firstly prove the function M(n), with
, we firstly prove the function M(n), with

in Eqs (20) and (21), is a monotonically decreasing function of n. The details for illustrating the monotonic property are presented in Methods.
Let

After some deduction, we can derive

when  . Thus, combining with the monotonically decreasing property of M(n), we prove that α ≥ M(n) when n ≥ 77, while α ≤ M(n) when n ≤ 76. When α = 2, we get
. Thus, combining with the monotonically decreasing property of M(n), we prove that α ≥ M(n) when n ≥ 77, while α ≤ M(n) when n ≤ 76. When α = 2, we get

which means α ≥ M(n) when n ≥ 10, while α ≤ M(n) when n ≤ 9. Combining the above two inequations with Eqs (20) and (21), we obtain the two bounds  and
and  . And, we know that
. And, we know that  when n ≥ N1 and
when n ≥ N1 and  when n ≤ N2. Then we complete the proof that
when n ≤ N2. Then we complete the proof that  obeys these properties.
obeys these properties.
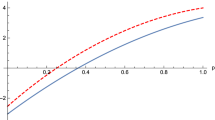
In Fig. 1, we plot these indicators as functions of n and then these properties can be verified from the figure. From the Fig. 1, we numerically find that  is a monotonically decreasing function of n when
is a monotonically decreasing function of n when  and n ≥ 10. How to exactly prove the result is an open problem.
and n ≥ 10. How to exactly prove the result is an open problem.
These results still hold for symmetric n-qubit mixed states as shown in the next part.
For the superpositions of the GHZ state and the W state
When an n-qubit mixed state is a superpositions of the GHZ state and the W state, it has the form

where  and
and  . For n = 3, Lohmayer et al.5 found that, when
. For n = 3, Lohmayer et al.5 found that, when  , it is entangled but without two-qubit concurrence and three-tangle. It is still an unsolved problem4 of how to characterize the entanglement structure in this kind of states for large n.
, it is entangled but without two-qubit concurrence and three-tangle. It is still an unsolved problem4 of how to characterize the entanglement structure in this kind of states for large n.
In Eq. (18), the n-partite entanglement indicators have the forms

Then, the calculations of  and
and  are key steps.
are key steps.
Any reduced two-qubit states of  has the same form
has the same form

Using the effective method for calculating concurrence in ref. 15 and after some calculations, we have

where n ≥ 6 and  . Then, according to Eq. (6), we obtain
. Then, according to Eq. (6), we obtain  .
.
In the following, we will calculate  . Through introducing a system B which has the same state space as the composite system
. Through introducing a system B which has the same state space as the composite system  ,
,  can be purified as
can be purified as

According to the Koashi-Winter formula4,18, the bipartite multiqubit EoF can be calculated by the purified state  , with
, with  ,
,

where  is the quantum conditional von Neumann entropy and the quantum discord
is the quantum conditional von Neumann entropy and the quantum discord  is defined as13
is defined as13

with the minimum running over all the positive operator-valued measures on the subsystem B. The details for proving Eq. (35) are presented in Methods. Chen et al.19 presented an effective method for choosing an optimal measurement over B and then calculating the quantum discord of two-qubit X states, which can be used to quantify the multipartite entanglement indicator in Eq. (19). After some analysis, we can obtain the optimal measurement for the quantum discord  is σz when n ≥ 6 and
is σz when n ≥ 6 and  . Then, after some deduction, we get
. Then, after some deduction, we get

From Eqs (19), (31) and (33), the indicator has the form

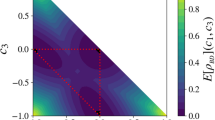
The distribution of  has been shown in Fig. 2 for
has been shown in Fig. 2 for  and α = 2 respectively. Furthermore,
and α = 2 respectively. Furthermore,  and
and  have some properties as follows.
have some properties as follows.
1. For any α,  is a monotonically decreasing function of n. The monotonically decreasing property of
is a monotonically decreasing function of n. The monotonically decreasing property of  holds because the first-order partial derivative satisfies
holds because the first-order partial derivative satisfies 
2. Combining with Theorem 3 and Eqs (33) and (38), we have  .
.
From the above two properties, we know that the nonzero  can indicate the existence of the n-qubit entanglement. These results can also be understood as the fact that
can indicate the existence of the n-qubit entanglement. These results can also be understood as the fact that  can detect as many as possible n-qubit entangled states for large n.
can detect as many as possible n-qubit entangled states for large n.
Conclusion
Entanglement monogamy is a fundamental property of multipartite entangled states. Based on our established monogamy relations Eq. (10), we obtain a set of useful tools for characterizing the multipartite entanglement not stored in pairs of the focus particle and the other subset of particles, which overcome some flaws of the concurrence. For any n-qubit symmetric state, we prove that the  indicator work best when n is large enough, while the 2 EoF indicator works better than the
indicator work best when n is large enough, while the 2 EoF indicator works better than the  indicator for smaller n.
indicator for smaller n.
Methods
The monotonic property of the function in Eqs (20) and (21)
In order to determine the monotonic property of M(n), with

in Eqs (20) and (21), we analyze the sign of the first-order derivative dM(n)/dn.
After some deduction, we can obtain

Then, dM(n)/dn < 0 when

and

Eq. (42) holds if and only if

i.e.,

The inequality (45) holds because  is a concave function of n with
is a concave function of n with  .
.
Similarly, we have Eq. (43) holds when

where

and then  . From ref. 9, we easily get that dt(n)/dn < 0 where
. From ref. 9, we easily get that dt(n)/dn < 0 where  .
.
In the following, we will prove Eq. (46). Let  , where
, where  . Using the definition of the partial derivative, it is not different to verify that
. Using the definition of the partial derivative, it is not different to verify that  ,
,  ,
,  and
and  are all continuous functions. Combining with the exchange order theorem of two second-order mixed partial derivative, we have
are all continuous functions. Combining with the exchange order theorem of two second-order mixed partial derivative, we have

According to Eq. (47), we get that F(t) is monotonic and concave as a function of t.
Combining with Eq. (19), we have

Here, the first inequality holds because f is a concave function of n and the monotonically increasing property of F(t) in Eq. (48). The second inequality is satisfied because F(t) is a monotonically increasing function in Eq. (48) and ln x is a concave function of x. And the last inequality holds because F(t) is a concave function as proved in Eq. (48).
Then, we complete the proof that M(n) is a monotonically decreasing function of n.
Proof of the Eq. (35) in the Main Text
Purification can be done for any state  , because we can introduce a system B which has the same state space as system
, because we can introduce a system B which has the same state space as system  and define a pure state20 for the combined system
and define a pure state20 for the combined system

From ref. 21, we know

Combining with  , we can find that Eq. (35) is just Eq. (2) in ref. 17. More specifically,
, we can find that Eq. (35) is just Eq. (2) in ref. 17. More specifically,

Then, we complete the proof of the Eq. (35) in the Main Text.
Additional Information
How to cite this article: Liu, F. et al. Multipartite entanglement indicators based on monogamy relations of n-qubit symmetric states. Sci. Rep. 6, 20302; doi: 10.1038/srep20302 (2016).
References
Streltsov, A., Adesso, G., Piani, M. & Bruß, D. Are general quantum correlations monogamous? Phys. Rev. Lett. 109, 050503 (2012).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Coffman, V., Kundu, J. & Wootters, W. K. Distributed entanglement. Phys. Rev. A 61, 052306 (2000).
Bai, Y.-K., Xu, Y.-F. & Wang, Z. D. General monogamy relation for the entanglement of formation in multiqubit systems. Phys. Rev. Lett. 113, 100503 (2014).
Lohmayer, R., Osterloh, A., Siewert, J. & Uhlmann, A. Entangled three-qubit states without concurrence and three-tangle. Phys. Rev. Lett. 97, 260502 (2006).
Bai, Y.-K., Xu, Y.-F. & Wang, Z. D. Hierarchical monogamy relations for the squared entanglement of formation in multipartite systems. Phys. Rev. A 90, 062343 (2014).
Zhu, X.-N. & Fei, S.-M. Entanglement monogamy relations of qubit systems. Phys. Rev. A 90, 024304 (2014).
Maccone, L., Bruß, D. & Macchiavello, C. Complementarity and correlations. Phys. Rev. Lett. 114, 130401 (2015).
Osborne, T. J. & Verstraete, F. General monogamy inequality for bipartite qubit entanglement. Phys. Rev. Lett. 96, 220503 (2006).
Bai, Y.-K., Ye, M.-Y. & Wang, Z. D. Entanglement in a class of multiqubit mixed states without multipartite tangles. Phys. Rev. A 78, 062325 (2008).
de Oliveira, T. R., Cornelio, M. F. & Fanchini, F. F. Monogamy of entanglement of formation. Phys. Rev. A 89, 034303 (2014).
Salinia, K., Prabhub, R., Sen(De), A. & Sen, U. Monotonically increasing functions of any quantum correlation can make all multiparty states monogamous. Ann. Phys. 348, 297 (2014).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Henderson, L. & Vedral, V. Classical, quantum and total correlations. J. Phys. A 34, 6899 (2001).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245 (1998).
Peres, A. Higher order schmidt decompositions. Phys. Lett. A 202, 16 (1995).
Kim, J. S. & Sanders, B. C. Generalized W-class state and its monogamy relation. J. Phys. A: Math. Gen. 41, 495301 (2008).
Koashi, M. & Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 69, 022309 (2004).
Chen, Q., Zhang, C., Yu, S., Yi, X. X. & Oh, C. H. Quantum discord of two-qubit X states. Phys. Rev. A 84, 042313 (2011).
Horodecki, M. & Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 59, 4206 (1999).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655 (2012).
Acknowledgements
This work is supported by NSFC (Grant Nos 61272057, 61170270), Beijing Higher Education Young Elite Teacher Project (Grant Nos YETP0475, YETP0477), the Natural Science Foundation of Shaanxi Province of China (Grant No. 2015JM6263) and Shandong Provincial Natural Science Foundation, China (Grant No. ZR2015FQ006).
Author information
Authors and Affiliations
Contributions
F.L. and F.G. contributed the idea. F.L. performed the calculations and wrote the main manuscript. S.-J.Q. checked the calculations. S.-C.X. and Q.-Y.W. made an improvement of the manuscript. All authors contributed to discussion and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, F., Gao, F., Qin, SJ. et al. Multipartite entanglement indicators based on monogamy relations of n-qubit symmetric states. Sci Rep 6, 20302 (2016). https://doi.org/10.1038/srep20302
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep20302
This article is cited by
-
A Proof for the Existence of Nonsquare Unextendible Maximally Entangled Bases
International Journal of Theoretical Physics (2018)
-
Uncertainty-like relations of the relative entropy of coherence
Quantum Information Processing (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

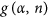 is a monotonically decreasing function of α.
is a monotonically decreasing function of α. is a monotonically decreasing function of α if and only if
is a monotonically decreasing function of α if and only if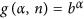 . Because 0 < b ≤ 1,
. Because 0 < b ≤ 1, 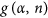 is a monotonically decreasing function of α.
is a monotonically decreasing function of α.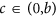 , we have
, we have
 in (a) and
in (a) and  in (b).
in (b).
 , α = 2 and
, α = 2 and  respectively.
respectively.