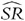Abstract
Until recently, since Jobson and Korkie (1981), derivations of the asymptotic distribution of the Sharpe ratio that are practically useable for generating confidence intervals or for conducting one- and two-sample hypothesis tests have relied on the restrictive, and now widely refuted, assumption of normally distributed returns. This paper presents an easily implemented formula for the asymptotic distribution that is valid under very general conditions — stationary and ergodic returns — thus permitting time-varying conditional volatilities, serial correlation, and other non-iid returns behaviour. It is consistent with that of Christie (2005), but it is more mathematically tractable and intuitive, and simple enough to be used in a spreadsheet. Also generalised beyond the normality assumption is the small sample bias adjustment presented in Christie (2005). A thorough simulation study examines the finite sample behaviour of the derived one- and two-sample estimators under the realistic returns conditions of concurrent leptokurtosis, asymmetry, and importantly (for the two-sample estimator), strong positive correlation between funds, the effects of which have been overlooked in previous studies. The two-sample statistic exhibits reasonable level control and good power under these real-world conditions. This makes its application to the ubiquitous Sharpe ratio rankings of mutual funds and hedge funds very useful, since the implicit pairwise comparisons in these orderings have little inferential value on their own. Using actual returns data from 20 mutual funds, the statistic yields statistically significant results for many such pairwise comparisons of the ranked funds. It should be useful for other purposes as well, wherever Sharpe ratios are used in performance assessment.













Similar content being viewed by others
Notes
Christie (2005) refers to the Sharpe ratio as ‘ubiquitous in the finance industry … arguably the most widely used general measure of fund manager performance’ (p. 5). McLeod and van Vuuren describe how it ‘quickly gained widespread popular acceptance and today enjoys almost ubiquitous implementation in the financial world’ (p. 1). And Lo (2002) calls it ‘one of the most commonly cited statistics in financial analysis’ (p. 1). In light of such assessments, it would appear difficult to overstate the importance of correctly understanding the statistical properties of the Sharpe ratio.
Although this is not true when excess returns are negative, many argue that the interpretation of the Sharpe ratio under these conditions does not change: a larger Sharpe ratio still indicates a better risk-adjusted performance (see Sharpe, 1998; Vinod & Morey, 2000; Akeda, 2003). Others disagree (see Scholz, 2007).
Eling and Schuhmacher (2007) present strong new evidence, even under the highly non-normal data conditions of hedge fund returns, in support of the Sharpe ratio compared to other more complex risk-adjusted performance metrics, the statistical properties of most of which are far less well understood.
Scherer (2004) believes that this is due to ‘the extreme difficulty of working out the required statistics for most risk-return ratios’ and yet the derivations presented herein are fairly straightforward.
Treating the risk-free rate as a constant is further justified by the fact that, even when its variance is not literally zero over the time period being examined, its covariance with stocks or funds will be.
In their letters to the editor of the Financial Analysts Journal, Morillo and Pohlman (2002) point out the earlier, identical result of Jobson and Korkie (1981), and Wolf (2003) points out that Lo's (2002) ‘iid’ derivation is valid only under normality. Lo (2003) acknowledges both points in his response, but emphasises the illustrative nature of his (normal) ‘iid’ derivation while urging readers to instead use his more robust GMM estimator when analysing actual financial data. Lo's (2002) GMM estimator, however, is not a simple formulaic solution and requires a modestly complex computer program to implement (ie Newey and West's (1987) procedure). Both these shortcomings to quick, simple, and practical implementation are overcome by the one-and two-sample estimators derived in this paper.
Also note that the term ¼(y4−1), obtained after combining the SR2 terms in (3), may be recognised as the relative variance of the estimate of the standard deviation, ς̂ (see Hansen et al. (1953), pp. 99, 102).
It is very important to note, however, that there appears to be growing empirical evidence for many financial instruments that the fourth moment of returns sometimes simply does not exist — kurtosis diverges rather than converges as sample sizes (the number of periods) increase (see Gençay et al., 2001). While this may be related to the (high) frequency of the returns data examined, it is an important potential limitation of using and the related derivations in this paper, as well as other statistical approaches, when making inferences about
 .
.Bao and Ullah (2006) also recently presented a derivation of the distribution of the Sharpe ratio that does not require a presumption of independence, but it does require normality, and so it is much less general than Christie's (2005) derivation, and less useful in practice given the vast empirical evidence in the finance literature that returns are non-normal. And as mentioned above, Lo's (2002) GMM estimator, while not requiring iid returns, is not a simple formulaic solution, but rather requires a modestly complex computer program to implement (ie Newey and West's (1987) procedure), making it less preferable to Christie's (2005) formulaically straightforward estimator.
As noted in Appendix B, the presumption of a constant risk-free rate, or an essentially constant risk-free rate, is required for this simplification. As an empirical matter, this assumption is justified.
In addition to being more easily calculated and understandable, (6), unlike (4), makes readily apparent the requirement of the existence of third and fourth moments (in addition to stationarity and ergodicity). As mentioned above, the fourth moment does not appear to exist for some financial instruments (see Gençay et al., 2001; Jondeau and Rockinger, 2003), in which case transformations to normality sometimes may be a viable alternative (eg, see Malevergne and Sornette, 2005).
Common practice in the financial services sector notwithstanding, dividing by T−1, rather than T, in the standard error will provide a less biased, albeit still slightly biased, estimate of the population standard error (see Zar, 1999, p. 39).
The fact that the distribution of the Sharpe ratio (6) takes into account higher moments of the returns distribution (ie skewness and kurtosis) at least partially mitigates criticism of the Sharpe ratio for not explicitly incorporating such moments into its actual formula (which, of course, is based only on the mean and the standard deviation). And as noted previously, Eling and Schuhmacher (2007) present strong new evidence, even under the ‘difficult’ data conditions of highly non-normal hedge fund returns, that the Sharpe ratio performs virtually identically to far more complex metrics that attempt, with mixed success, to explicitly incorporate higher moments.
Of course, this is not the only approach. To test this two-sample hypothesis, Christie (2005) jointly tests, consistent with his asymptotic derivation, moment restrictions within a single system of moment restrictions. However, the benefits of this paper's approach over Christie's (2005) GMM approach are two-fold: (i) implementation of the former does not require custom coding a moderately complex statistical software program (rather, it can be implemented in a spreadsheet), and (ii) it provides confidence intervals as well as p-values, while Christie's (2005) approach provides only p-values. While Vinod and Morey's (2000) bootstrap approach does not require derivation of the distribution of the difference between Sharpe ratios, it does require a computationally intensive computer program (and a very computationally intensive program for their double bootstrap method), and may be less powerful than the asymptotic approach adopted in this paper. In addition, it should be noted that the variance estimates produced by many bootstrap procedures have been shown in the literature to be notoriously poor under asymmetric heavy tails, and even under symmetric heavy tails (see Rocke and Downs, 1981; Gosh et al., 1984; Salibián-Barrera, 1998), and these are the defining characteristics of financial market returns. Consequently, in the absence of a rigorous, validating bootstrap simulation study providing results based on simulated returns of known distributions rather than actual returns data, such bootstrap variance estimators of Sharpe ratios should be interpreted with caution.
The joint moment terms of (13), for ρ≠0, are very accurately estimated in simulations of N=100,000.
Although one might be tempted to say that the distribution of
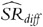 under a naïve assumption of normality with no between-fund correlation (Figure 2a) is virtually identical to that under more realistic distributional conditions and a strong positive correlation (Figure 2b), this is only true asymptotically. In practice, using actual finite data samples, these two distributions are very different, and the simplifying but naïve (and incorrect) assumption of normality can lead to very misleading inferences.
under a naïve assumption of normality with no between-fund correlation (Figure 2a) is virtually identical to that under more realistic distributional conditions and a strong positive correlation (Figure 2b), this is only true asymptotically. In practice, using actual finite data samples, these two distributions are very different, and the simplifying but naïve (and incorrect) assumption of normality can lead to very misleading inferences.This is not to be confused with the skew-normal distribution of Azzalini (1985), which is very similar.
Similar densities recently have been developed, such as the asymmetric exponential power (AEP) distribution of Ayebo and Kozubowski (2003), and the Gauss–Laplace Mixture (GLaM) and Gauss–Laplace Sum (GLaS) distributions used by Haas et al. (2005).
Graphically, Figure 3 is very similar to the empirically estimated skew-normal density used by Vinod (2005) (p. 854) (Vinod used Azzalini, 1985) and has similar coefficients of skewness and kurtosis. APD, however, not only is more flexible, since it nests a version of the skew normal, but also appears more appropriate from an empirical perspective, since Komunjer's (2006) hypothesis tests reject both the symmetric and asymmetric versions of the normal distribution using actual financial returns data. Hence, APD would appear to be the better choice.
For the one-sample power results, that is, when SR a ≠c, SR a =0.3, 0.4 also are included.
While a Cholesky decomposition will exactly preserve the linear correlations, it typically will not preserve the distributions of the returns.
Using biased but more efficient estimators for simulations is common statistical practice.
Complete simulation results of the 5,200 scenarios examined, for both one-and two-sided tests, are available from the author upon request.
In situations where many related hypothesis tests are being conducted and the cost of type I error (false positives) is high (eg genome research), multiple comparison procedures are often used to control the family-wise error rate (FWE) or the false discovery rate (FDR) rather than the pairwise error rate (ie, α). Although the objective here as shown in Table 4 is different — only to examine specific columns of interest individually — such procedures could be very useful in this setting if the hypotheses being examined do involve sizeable numbers of multiple comparisons. See J.D. Storey (2002, 2003, 2004, 2007) and J. Hsu (1996) for details.
Kelly (2007) relies on the Sharpe ratio, and the estimators derived herein ((6) and (13)), to test whether open-to-close ETF returns are different from close-to-open (after hours trading) ETF returns. He finds large differences with strong statistical significance.
Identical results were obtained when the variable risk-free rate was incorporated into the returns themselves, confirming that, as an empirical matter, the simplifying assumption of a constant risk-free rate is acceptable for practical usage.
This finding is similar to and consistent with that of Pastor and Stambaugh (2003), who showed that the use of returns of seemingly unrelated assets, which are often correlated with the particular fund being examined, can dramatically increase the precision with which one can estimate the SR of that particular fund, and that the estimate of SR can differ dramatically as a result.
As mentioned previously, even if the variance of the risk-free rate is not literally zero, as is often the case, as a practical empirical matter it can be treated as zero, and its arithmetic mean can be used as the presumed constant rate (so above, let R ft =μ̂ f =R f ). Covariances of the risk-free rate with fund returns, too, can be treated as zero as an empirical matter. Mathematically, these assumptions are necessary for the above simplification.
The delta method is a widely used technique that provides an asymptotic approximation of the variance of a particular function (see Greene, 1993, pp. 297–298; Stuart and Ord, 1994, p. 350). It is valid as long as the random variables used in the function are asymptotically normal, and the function is (loosely speaking) continuous and continuously differentiable. The former assumption is true in this case, since the sample mean and the sample variance are asymptotically normal. The latter assumption is clearly violated if the variance of returns is zero. This will never actually occur in practice using real data samples, but if the variance approaches zero, making the Sharpe ratio highly nonlinear, delta method estimates will become unstable, as correctly noted by Vinod and Morey (2000). However, this scenario, too, arguably will affect few, if any cases in practice, as the variances of the returns of most, if not all funds or stocks that would be of enough interest to be subjected to Sharpe ratio comparisons are quite far from zero; if they were not, there would be nothing to compare! Still, it is important to note the limitations of analytical methods relied upon in any study, in case their domain of application changes. Jobson and Korkie (1981), Lo (2002), Memmel (2003), and Mertens (2002) all use the delta method in their studies of Sharpe ratios, thus supporting its practical use here.
References
Akeda, Y. (2003) ‘Another Interpretation of Negative Sharpe Ratio’, The Journal of Performance Measurement, 7 (3), 19–23.
Ayebo, A. and Kozubowski, T. (2003) ‘An Asymmetric Generalization of Gaussian and Laplace Laws’, Journal of Probability and Statistical Science, 1 (2), 187–210.
Azzalini, A. (1985) ‘A Class of Distributions Which Includes the Normal Ones’, Scandinavian Journal of Statistics, 12, 171–178.
Bao, Y. and Ullah, A. (2006) ‘Moments of the Estimated Sharpe Ratio when the Observations are not IID’, Finance Research Letters, 3, 49–56.
Be, T. W. (2000) ‘Excess Kurtosis of Conditional Distribution for Daily Stock Returns: The Case of Japan’, Applied Economics Letters, 7 (6), 353–355.
Brännäs, K. and Nordman, N. (2003) ‘Conditional Skewness Modeling for Stock Returns’, Applied Economics Letters, 10, 725–728.
Cajigas, J. and Urga, G. (2005) ‘Dynamic Conditional Correlation Models with Asymmetric Multivariate Laplace Innovations’, presentation, Simulation Based and Finite Sample Inference in Finance II Conference in Quebec City, April 29–30.
Cappiello, L., Engle, R. and Sheppard, K. (2003) ‘Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns’, European Central Bank Working Paper Series, Working Paper No. 204.
Christie, S. (2005) ‘Is the Sharpe Ratio Useful in Asset Allocation?’, MAFC Research Papers No.31, Applied Finance Centre, Macquarie University.
Dillen, H. and Stoltz, B. (1999) ‘The Distribution of Stock Market Returns and the Market Model’, Finnish Economic Papers, 12 (1), 41–56.
Eling, M. and Schuhmacher, F. (2007) ‘Does the Choice of Performance Measure Influence the Evaluation of Hedge Funds’, Journal of Banking & Finance, 31 (9), 2632–2647.
Espejo, R. and Singh, H. (1999) ‘Covariance of Sample Moments for Simple Random Sampling with Replacement of a Finite Population’, Mathematical Proceedings of the Royal Irish Academy, 99A (2), 171–177.
Federal Reserve Board, data series TCMNOMM3, from http://www.federalreserve.gov/releases/h15/data.htm.
Gençay, R., Dacorogna, M., Muller, U., Pictet, O. and Olsen, R. (2001) An Introduction to High-Frequency Finance, Academic Press, San Diego.
Getmansky, M., Lo, A. and Makarov, I. (2004) ‘Model of Serial Correlation and Illiquidity in Hedge-Fund Returns’, Journal of Financial Economics, 74 (3), 529–609.
Gosh, M., Parr, W., Singh, K. and Babu, G. (1984) ‘A Note on Bootstrapping the Sample Median’, The Annals of Statistics, 12, 1130–1135.
Greene, W. (1993) Econometric Analysis, 2nd edn, Macmillan Publishing Company, New York.
Haas, M., Mittnik, S. and Paolella, M. (2005) ‘Modeling and Predicting Market Risk with Laplace–Gaussian Mixture Distributions’, CFS Working Paper No. 2005/11, Center for Financial Studies, Ifo Institute for Economic Research.
Halmös, P. (1946) ‘The Theory of Unbiased Estimation’, Annals of Mathematical Statistics, 17, 34–43.
Hansen, M. H., Hurwitz, W. N. and Madow, W. G. (1953), in Walter Shewhart (ed.), Sample Survey Methods and Theory, John Wiley & Sons, Inc., New York.
Harris, R. D. F. and Coskun, K. (2001) ‘The Empirical Distribution of Stock Returns: Evidence from an Emerging European Market’, Applied Economics Letters, 8, 367–371.
Hennard, Y. and Aparicio, M. (2003) ‘Multi-class Asset Allocation for Swiss Institutional Investors’, Masters Thesis, Universite de Lausanne, Ecole des Hautes Etudes Commerciales (HEC), Master of Science in Finance.
Hsu, J. (1996) Multiple Comparisons, Chapman & Hall/CRC, New York.
Jobson, J. and Korkie, B. (1981) ‘Performance Hypothesis Testing with the Sharpe and Treynor Measures’, The Journal of Finance, 36 (4), 889–908.
Johnson, N., Kotz, S. and Balakrishnan, N. (1994) Continuous Univariate Distributions, 2nd edn, Wiley, New York.
Jondeau, E. and Rockinger, M. (2003) ‘Conditional Volatility, Skewness, and Kurtosis: Existence, Persistence, and Comovements’, Journal of Economic Dynamics and Control, 27 (10), 1699–1737.
Kelly, M. (2007) ‘Returns in Trading versus Non-Trading Hours: The Difference is Day and Night’, Lafayette College, Working Paper.
Kmenta, J. (1986) Elements of Econometrics, 2nd edn, Macmillan Publishing Company, New York.
Knight, J. and Satchell, S. (2005) ‘A Re-Examination of Sharpe's Ratio for Log-Normal Prices’, Applied Mathematical Finance, 12 (1), 87–92.
Komunjer, I. (2006) ‘Asymmetric Power Distribution: Theory and Applications to Risk Measurement’, Journal of Applied Econometrics, 22 (5), 891–921.
Kotz, S., Kozubowski, T. and Podgorski, K. (2001) The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance, Birkhäuser, Boston.
Kozubowski, T. and Podgorski, K. (1999) ‘A Class of Asymmetric Distributions’, Actuarial Research Clearing House, 1, 113–134.
Kozubowski, T. and Podgorski, K. (2001) ‘Asymmetric Laplace Laws and Modeling Financial Data’, Mathematical and Computer Modeling, 34, 1003–1021.
Lee, Y. (2003), Society of Actuary Annual Meeting 2003, Keynote: “Diversification with Fund of Hedge Funds”.
Linden, M. (2001) ‘A Model for Stock Return Distribution’, International Journal of Finance & Economics, 6 (2), 159–169.
Lo, A. W. (2002) ‘The Statistics of Sharpe Ratios’, Financial Analysts Journal, 58 (4), 36–52.
Lo, A. W. (2003) ‘The Statistics of Sharpe Ratios: Author's Response’, Financial Analysts Journal, 59 (5), 17–17.
Malevergne, Y. and Sornette, D. (2005) ‘High-Order Moments and Cumulants of Multivariate Weibull Asset Returns Distributions: Analytical Theory and Empirical Tests: II’, Finance Letters, 3 (1), 54–63.
McLeod, W. and van Vurren, G. (2004) ‘Interpreting the Sharpe Ratio when Excess Returns are Negative’, Investment Analysts Journal, 59, 15–20.
Memmel, C. (2003) ‘Performance Hypothesis Testing with the Sharpe Ratio’, Finance Letters, 1, 21–23.
Mertens, E. (2002) ‘Comments on the correct variance of estimated Sharpe Ratios in Lo (2002, FAJ) when returns are IID’, Research Note (www.elmarmertens.org).
Miller, R. and Gehr, A. (1978) ‘Sample Bias and Sharpe's Performance Measure: A Note’, Journal of Financial and Quantitative Analysis, 13, 943–946.
Morillo, D. and Pohlman, L. (2002) ‘The Statistics of Sharpe Ratios: A Comment’, Financial Analysts Journal, 58 (6), 18–18.
Newey, W. and West, D. (1987) ‘A Simple, Positive Semi-Definite, Heteroscedasticity and Autocorrelation Consistent Covariance Matrix’, Econometrica, 55, 703–708.
Pastor, L. and Stambaugh, R. (2003) ‘Mutual Fund Performance and Seemingly Unrelated Assets’, Journal of Financial Economics, 63 (3), 315–349.
Patterson, K. D. and Heravi, S. (2003) ‘The Impact of Fat-tailed Distributions on Some Leading Unit Root Tests’, Journal of Applied Statistics, 30, 635–667.
Pinto, J. and Curto, J. (2005) ‘The Generalized Method of Moments: An Application to the Sharpe Ratio’, Temas em Métodos Quantitativos (Subjects in Quantitative Methods), 5, 1–13 (forthcoming).
Randles, R. and Wolfe, D. (1979) Introduction to the Theory of Nonparametric Statistics, John Wiley & Sons, New York.
Richardson, M. and Smith, T. (1993) ‘A Test for Multivariate Normality in Stock Returns’, Journal of Business, 66 (2), 295–321.
Rocke, D. and Downs, G. (1981) ‘Estimating the Variances of Robust Estimators of Location: Influence Curve, Jackknife and Bootstrap’, Communications in Statistics — Simulation and Computation, 10 (3), 221–248.
Rose, C. and Smith, M. (2002) Mathematical Statistics with Mathematica, Springer-Verlag, New York.
Salibián-Barrera, M. (1998) ‘On Globally Robust Confidence Intervals for Regression Coefficients’, Technical Report #176, The University of British Columbia Department of Statistics.
Scherer, B. (2004) ‘An Alternative Route to Performance Hypothesis Testing’, Journal of Asset Management, 5, 5–12.
Scholz, H. (2007) ‘Refinements to the Sharpe Ratio: Comparing Alternatives for Bear Markets’, Journal of Asset Management, 5, 5–12.
Sharpe, W. (1966) ‘Mutual Fund Performance’, Journal of Business 39 (January), 119–138.
Sharpe, W. (1975) ‘Adjusting for Risk in Portfolio Performance Measurement’, Journal of Portfolio Management (Winter), 29–34.
Sharpe, W. (1994) ‘The Sharpe Ratio’, Journal of Portfolio Management (Fall), 49–58.
Sharpe, W. (1998) ‘Morningstar's Risk Adjusted Ratings’, Financial Analyst Journal 54(4) (July/August), 21–33.
Smith, P. (1995) ‘A Recursive Formulation of the Old Problem of Obtaining Moments From Cumulants and Vice Versa’, The American Statistician, 49 (2), 217–218.
Storey, J. D. (2002) ‘The Positive False Discovery Rate: A Bayesian Interpretation and the q-Value’, The Annals of Statisticis, 31 (6), 2013–2035.
Storey, J. D. (2003) ‘A Direct Approach to False Discovery Rates’, Journal of the Royal Statistical Society, Series B, 64 (Part 3), 479–498.
Storey, J. D. (2004) ‘Strong Control, Conservative Point Estimation and Simultaneous Conservative Consistency of False Discovery Rates: A Unified Approach’, Journal of the Royal Statistical Society, Series B, 66 (Part 1), 187–205.
Storey, J. D. (2007) ‘The Optimal Discovery Procedure: A New Approach to Simultaneous Significance Testing’, Journal of the Royal Statistical Society, Series B, 69 (Part 3), 347–368.
Stuart, A. and Ord, K. (eds.) (1994) Kendall's Advanced Theory of Statistics, Vol. 1 Distribution Theory, 6th edn., New York, Oxford University Press.
Vinod, H. (2005) ‘Skew Densities and Ensemble Inference for Financial Economics’, The Mathematica Journal, 9 (4), 852–862.
Vinod, H. and Morey, M. (2000) ‘Confidence Intervals and Hypothesis Testing for the Sharpe and Treynor Performance Measures: A Bootstrap Approach’, in Yaser S. abu-Mostafa, Blake LeBaron, Andrew W. Lo, and Andreas S. Weigend (eds.), Computational Finance 1999, The MIT Press, Cambridge, MA.
White, H. (2001) Asymptotic Theory for Econometricians, Revised edn, Academic Press, San Diego.
Wolf, M. (2003) ‘The Statistics of Sharpe Ratios: A Comment’, Financial Analysts Journal, 59 (5), 17–17.
Yahoo — Finance, http://finance.yahoo.com data on returns from 40 mutual funds.
Zar, J. (1999) Biostatistical Analysis, 4th edn., Prentice-Hall, Upper Saddle River, NJ.
Acknowledgements
I express my gratitude to Keith Ord, Hrishikesh Vinod, and Andrew Clark for useful comments, and sincere appreciation to Steve Christie for spotting an error in an earlier draft.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Alternate derivation of the distribution of 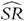 under IID via the delta method
under IID via the delta method
According to Stuart and Ord (1994), pp. 350–352, the ‘delta method’ can be used to derive the variance of a function, g(x1, x2, x3, …), of a number of random variables, and if the function is the ratio of two random variables, then:

If x1=μ and x1=σ then


since x1=μ−R ft yields the same results above, we can treat μ/σ=SR, and so


which is Merten's (2002) result. The more technical conditions required for the valid use of the delta method are discussed in Appendix C.
Appendix B
Equivalence of Merten's (2002) iid, and Christie's (2005) GMM, derivations of the distribution of 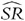
Under only the requirements of stationarity and ergodicity, Christie (2005) derives (C21),

which can be simplified as below:Footnote 28

since E[R t 2]=σ2+μ2,

since E[R t 3]=μ3+3σ2μ+μ3,

So  , which is Merten's (2002) result, and that derived in Appendix A.
, which is Merten's (2002) result, and that derived in Appendix A.
Appendix C
Variance of the difference between two Sharpe ratios
If SR
a
and SR
b
are the respective Sharpe ratios for the returns (R
at
and R
bt
) of funds ‘a’ and ‘b,’ then use the ‘delta method’Footnote 29 (see Greene, 1993; Stuart and Ord, 1994) to obtain the asymptotic variance of  : Assuming σ
f
2=0, which is always essentially, if not literally true, SR=μ−R
f
/σ=f(μ, σ2), and so let u=(μ
a
, μ
b
, σ
a
2, σ
b
2) and û=(μ̂
a
, μ̂
b
, ς̂
a
2, ς̂
b
2), then,
: Assuming σ
f
2=0, which is always essentially, if not literally true, SR=μ−R
f
/σ=f(μ, σ2), and so let u=(μ
a
, μ
b
, σ
a
2, σ
b
2) and û=(μ̂
a
, μ̂
b
, ς̂
a
2, ς̂
b
2), then,  where Ω is the variance–covariance matrix of u:
where Ω is the variance–covariance matrix of u:

where σa, b=Cov(a, b), μ3a=E[(a−μ
a
)3]=Cov(μ
a
, σ
a
2), μ3b=E[(b−μ
b
)3]=Cov(μ
b
, σ
b
2) (see Mertens, 2002), μ1a, 2b=E[(a−μ
a
)(a−μ
b
)2]=Cov(μ
a
, σ
b
2), and μ1b, 2a=E[(b−μ
b
)(a−μ
a
)2]=Cov(μ
b
, σ
a
2) (see Espejo and Singh, 1999). Now,  ,
,



Since =Var(σ a 2)=Cov (σ a 2, σ a 2) =μ4a−σ a 4=E [(a−E[a])4]−σ a 4 =E[(a−E[a])2(a−E[a])2]−σ a 2σ a 2, then Cov(σ a 2, σ b 2)=E[(a−E[a])2(b−E [b])2]−σ a 2σ b 2=μ2a, 2b−σ a 2σ b 2, whereμ2a, 2b is the second central moment of the joint distribution of a and b. The same result can be obtained using Stuart and Ord's (1994) (pp.457–458) result of Cov(ς̂ a 2, ς̂ b 2)=κ2a, 2b/n+2κ1a, 1b2/(n−1), where κ2a, 2b is the second joint cumulant of the joint distribution of a and b, and κ1a, 1b is the first joint cumulant, equal to the first joint central moment, μ1a, 1b, which is the covariance. Dropping the n coefficients due to the use of the estimators ς̂ a 2, ς̂ b 2 for σ a 2, σ b 2 yields Cov(σ a 2, σ b 2)=κ2a, 2b/n+2κ1a, 1b2 =κ2a, 2b+2μ1a, 1b2=κ2a, 2b+2σa, b2. Recognising that the joint cumulant can also be expressed in terms of central moments, κ2a, 2b=μ2a, 2b−μ2a, 0 × μ0, 2b −2μ1a, 1b2=μ2a, 2b−σ a 2, σ b 2−2σa, b2 (see Stuart and Ord, 1994, p. 107, and Smith, 1995), we have:

Thus,

Hence, analogous to the variance of the distribution of a single  , (6), the variance of the difference between two
, (6), the variance of the difference between two  is
is

Note that when ρa, b=0, μ2a, 2b=σ a 2σ b 2, μ1a, 2b=0, and μ1b, 2a=0, and so the entire covariance term of Var diff disappears, as it should.
Minimum variance unbiased estimators of μ1a, 2b, μ1b, 2a, & μ2a, 2b are the respective h-statistics h1a, 2b, h1b, 2a, & h2a, 2b, where h1, 2=[2s0, 12s1, 0−ns0, 2s1, 0−2s0, 12s1, 1 −n2s1, 2]/[n(n−1)(n−2)], and h2, 2=[−3s0, 12s1, 02 +ns0, 2s1, 02+4ns0, 1s1, 0s1, 1−2(2n−3)s1, 12−2(n2−2n+3)s1, 0s1, 2+s0, 12s2, 0(2n−3)s0, 2s2, 0−2(n2−2n+3) s0, 1s2, 1+n(n2−2n+3)s2, 2]/[(n−3)(n−2)(n−1)n], where sx, y are the simple power sums of sx, y=∑i=1na i xb i y (see Rose and Smith, 2002, pp. 259–260).
This derivation is valid under iid returns, but because the one-sample estimator (6), derived using the same (delta) method (a la Mertens, 2002), was shown in Appendix B to be valid under the more general conditions afforded by its (identical) GMM derivation (a la Christie, 2005), we suspect that those more general conditions of stationarity and ergodicity are the only requirements for the two-sample estimator of (13) as well. Proving this is the topic of continuing research.
Appendix D
Equivalence of Var diff with Memmel (2003) and Jobson and Korkie (1981)
Under iid normality, Memmel's (2003) correction of Jobson and Korkie's (1981) variance of the two-sample statistic for the difference between two Sharpe ratios is:

Under iid normality, TV is identical to Var diff , as shown below:

Under iid normality, μ3/σ3=0, μ1, 2=0, μ4/σ4=3, & μ2a, 2b=(1+2ρa, b2)σ a 2σ b 2 (see Stuart and Ord, 1994, p. 105), so

which is Memmel's (2003) result.
Appendix E
Simulation distributions: APD of Komunjer (2006)
Komunjer (2006) gives the density of the APD below:

where 0<α<1, λ>0, and δα, λ=2αλ(1−α)λ/αλ+(1−α)λ
The α parameter (0<α<1) controls skewness, with symmetry at α=0.5, and λ>0 controls kurtosis, such that when α=0.5, λ= → the uniform distribution, λ=1.0 → the Laplace distribution (with variance=2.0), λ=2.0 → the normal distribution (with variance=0.5) and any λ → the Generalised Power Distribution. When α≠0.5, λ=1.0 → the Asymmetric Laplace distribution of Kozubowski and Podgorski (1999), and λ=2.0 → the two-piece normal distribution (see Johnson et al., 1994, vol. 1, p. 173 and vol. 2, p. 190). This does APD allow simultaneous control over skewness and kurtosis, nesting the normal and Laplace densities, and asymmetric versions of each, as well as any ‘in between’ combination of asymmetry and kurtosis (Figure E1).
Location and scale are accommodated via the simple transformation: X≡θ+φU
APD moments are given by:

(see Table E1). So for example,

and

To standardise the APD for the simulations presented in this study, U is modified by u′=u/sqrt[Var(u)] (because, for example, when α=0.5 and λ=1.0, Var(U)=2.0, and when α=0.5 and λ=2.0, Var(U)=0.5).
Rights and permissions
About this article
Cite this article
Opdyke, J. Comparing Sharpe ratios: So where are the p-values?. J Asset Manag 8, 308–336 (2007). https://doi.org/10.1057/palgrave.jam.2250084
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jam.2250084




 .
.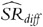 under a naïve assumption of normality with no between-fund correlation (
under a naïve assumption of normality with no between-fund correlation (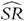 under IID via the delta method
under IID via the delta method