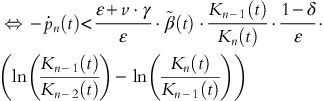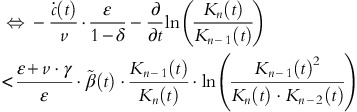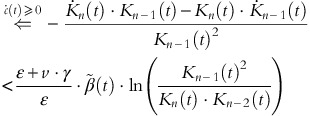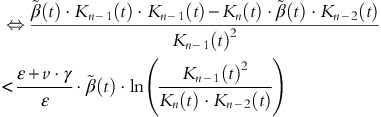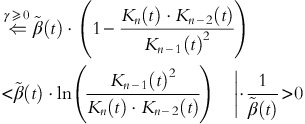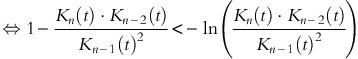Abstract
This article analyzes a dynamic pricing and advertising model for the sale of perishable products under constant absolute risk aversion. We consider a time-dependent version of Gallego and van Ryzin’s dynamic pricing model with exponential demand and include isoelastic advertising effects as well as marginal unit costs. We derive closed-form expressions of the optimal risk-averse pricing and advertising policies of the value function and of the certainty equivalent. The formulas provide insight into the (complex) interplay between risk-sensitive pricing and advertising decisions. Moreover, to evaluate the optimally controlled sales process over time we propose efficient simulation techniques. These are used to analyze the characteristics of different degrees of risk aversion, particularly the concentration of the profit distribution and the impact on the expected evolution of price and advertising rates.







Similar content being viewed by others
References
Barz, C. and Waldmann, K.-H. (2007) Risk-sensitive capacity control in revenue management. Mathematical Methods of Operations Research 65 (3): 565–579.
Bäuerle, N. and Rieder, U. (2014) More risk-sensitive Markov decision processes. Mathematics of Operations Research 39 (1): 105–120.
Bitran, G. and Caldentey, R. (2003) An overview of pricing models for revenue management. Manufacturing & Service Operations Management 5 (3): 203–229.
Chen, X., Sim, M., Simchi-Levi, D. and Sun, P. (2007) Risk aversion in inventory management. Operations Research 55 (5): 28–842.
Elmaghraby, W. and Keskinocak, P. (2003) Dynamic pricing in the presence of inventory considerations: Research overview, current practices, and future directions. Management Science 49 (10): 1287–1309.
Feng, Y. and Xiao, B. (2008) A risk-sensitive model for managing perishable products. Operations Research 56 (5): 1305–1311.
Gallego, G. and van Ryzin, G. (1994) Optimal dynamic pricing of inventories with stochastic demand over finite horizons. Management Science 40 (8): 999–1020.
Helmes, K. and Schlosser, R. (2013) Dynamic advertising and pricing with constant demand elasticities. Journal of Economic Dynamics and Control 37 (12): 2814–2832.
Helmes, K., Schlosser, R. and Weber, M. (2013) Dynamic advertising and pricing in a class of general new-product adoption models. European Journal of Operational Research 229 (2): 433–443.
Helmes, K. and Schlosser, R. (2014) Oligopoly pricing and advertising in isoelastic adoption models. Dynamic Games and Applications, Forthcoming doi:10.1007/s13235-014-0123-1.
Koenig, M. and Meissner, J. (2009) Risk Minimizing Strategies for Revenue Management with Target Values. Lancaster, UK: Lancaster University Management School.
Levin, Y., McGill, J. and Nediak, M. (2008) Risk in revenue management and dynamic pricing. Operations Research 56 (2): 326–343.
Lewis, P.A. and Shedler, G.S. (1979) Simulation of nonhomogeneous poisson processes by thinning. Naval Research Logistics Quarterly 26 (3): 403–413.
Li, M.Z.F. and Zhuang, W. (2009) Risk-sensitive dynamic pricing for a single perishable product. Operations Research Letters 37 (5): 327–332.
Lim, A.E.B. and Shanthikumar, J.G. (2007) Relative entropy, exponential utility and robust dynamic pricing. Operations Research 55 (2): 198–214.
MacDonald, L. and Rasmussen, H. (2010) Revenue management with dynamic pricing and advertising. Journal of Revenue and Pricing Management 9 (1–2): 126–136.
McAfee, R.P. and te Velde, V. (2006) Dynamic pricing in the airline industry. In T. Hendershott (ed.) Economics and Information Systems. Amsterdam, the Netherlands: Elsevier, pp. 527–570.
McAfee, R.P. and te Velde, V. (2008) Dynamic pricing with constant demand elasticity. Production and Operations Management 17 (4): 432–438.
Øksendal, B. and Sulem, A. (2005) Applied Stochastic Control of Jump Diffusions. 2nd edn. Berlin: Springer.
Pang, Z., Berman, O. and Hu, M. (2015) Up then down: The Bid-Price Trends in Revenue Management. Production and Operations Management. doi:10.1111/poms.12324.
Phillips, R. (2005) Pricing and Revenue Optimization. Stanford, CA: Stanford University Press.
Schlosser, R. (2015) Dynamic pricing with time-dependent elasticities. Journal of Revenue and Pricing Management. doi:10.1057/rpm.2015.3.
Sethi, S.P., Prasad, A. and He, X. (2008) Optimal advertising and pricing in a new-product adoption model. Journal of Optimization Theory and Applications 139 (2): 351–360.
Sethi, S.P. and Thompson, G.L. (2000) Optimal Control Theory: Applications to Management Science and Economics.2nd edn Boston, MA: Kluwer Academic Publishers.
Shen, Z.M. and Su, X. (2007) Customer behavior modeling in revenue management and auctions: A review and new research opportunities. Production Operations Management 16 (6): 713–728.
Talluri, K.T. and van Ryzin, G. (2004) The Theory and Practice of Revenue Management. Boston, MA: Kluwer Academic Publishers.
Xu, X. and Hopp, W.J. (2009) Price trends in a dynamic pricing model with heterogeneous customers: A Martingale perspective. Operations Research 57 (5): 1298–1302.
Yeoman, I. and McMahon-Beattie, U. (2011) Revenue Management: A Practical Pricing Perspective. Palgrave Macmillan.
Author information
Authors and Affiliations
Appendix
Appendix
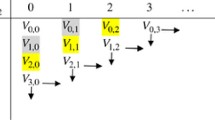
Model description
For any given admissible Markov policy (p, w), cf. the section ‘Model description’, the jump intensity in state (t, n, r) is given by λ n,r (t):=λ(t, p n,r (t), w n,r (t)). For all t, n and r let W(t, n, r):=u(r)=−e−γ⋅r. Using the Itô formula for jump processes and taking expectations we obtain

where A(p,w) is the generator that characterizes the dynamic of the three-dimensional Markovian process (t, X
t
, R
t
)0⩽t⩽T; (0, X0, R0)=(0, N, 0) is the starting state. Applied to a function F(t, n, r)≔g(t)⋅f(n)⋅h(r) (where g(t) and h(r) are differentiable functions with compact support), for given controls (p, w) A has the form, 0⩽t⩽T, 0⩽n⩽N,  ,
,

cf. Øksendal, Sulem (2005), Sec. 1. We want to show that the solution of the value function, cf. Theorem 3.1, is of the following separable form

where the function  is independent of r and differentiable in t for all n. Applying the generator A to (A.3), we obtain from (A.2)
is independent of r and differentiable in t for all n. Applying the generator A to (A.3), we obtain from (A.2)

If  is chosen such that it solves the non-linear difference-differential equation, n=1, …, N, 0⩽t<T,
is chosen such that it solves the non-linear difference-differential equation, n=1, …, N, 0⩽t<T,

with the boundary conditions

the policy (p*, w*)=(p n *(t), w n *(t)) determined by (A.4), cf. Theorem 3.1, maximizes the right-hand side of (A.1), and we obtain

Hence, for all policies (p, w)=(p n,r (t), w n,r (t)) we have

Thus,  is the value function J*(t, n, r). Moreover, using the relation
is the value function J*(t, n, r). Moreover, using the relation  , it follows from (A.4) – (A.5) that J*(t, n, r) satisfies the non-linear difference-differential equation, n=1, …, N, 0⩽t<T,
, it follows from (A.4) – (A.5) that J*(t, n, r) satisfies the non-linear difference-differential equation, n=1, …, N, 0⩽t<T,  ,
,

with the boundary conditions,  ,
,

The equation (A.6) is called the Hamilton-Jacobi-Bellman equation that is associated with the utility maximizing problem described in the section ‘Model description’.
Analytical solution
Proof of Proposition 3.1
-
In our special case with exponential demand, we compute the CARA version of the dynamic Dorfman–Steiner identity as follows. Following the definition of the sales rate, the ratio of optimal advertising rate and optimal rate of sales is,
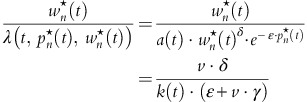
□
Proof of Theorem 3.1
-
Plugging the solution of the value function
 in the optimality condition for price, that is,
in the optimality condition for price, that is,  , cf. (7), we obtain, d≔ɛ/(v⋅(1−δ)),
, cf. (7), we obtain, d≔ɛ/(v⋅(1−δ)),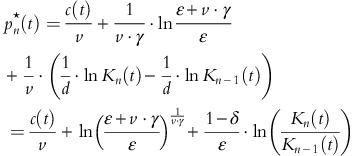
The explicit formula for optimal advertising rates
 can be derived by plugging the formula for optimal prices derived above into the optimality condition for optimal advertising rates, cf. (7):
can be derived by plugging the formula for optimal prices derived above into the optimality condition for optimal advertising rates, cf. (7):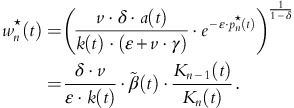
The optimal rate of sales λ n *(t) (cf. Theorem 3.1) can be computed via p n *(t) and w n *(t) as follows:
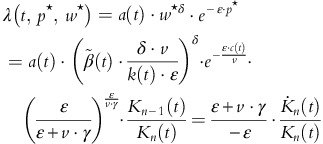
Simple algebra reveals that the function
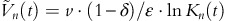 solves equation (8). Note that the optimal controls are associated with
solves equation (8). Note that the optimal controls are associated with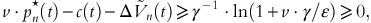
cf. (7), and thus the conditions
 and
and 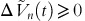 guarantee that p
n
*(t)⩾0 and w
n
*(t)⩾0. Consequently, the optimal controls are admissible. □
guarantee that p
n
*(t)⩾0 and w
n
*(t)⩾0. Consequently, the optimal controls are admissible. □
Expected evolution of optimal prices
Proof of Theorem 4.1
-
For sufficiently small h>0, the probability of the sale of one article between the time points t and t+h is approximately λ*(t)⋅h. At time t, with n items left, we consider the following inequality comparing the actual price p n (t)=c(t)/v+ln(1+v·γ/ɛ)/(v·γ)+(1−δ)/ɛ·ln(K n (t)/Kn−1(t)) and the expected future price in t+h:
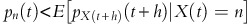
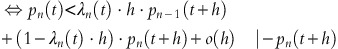
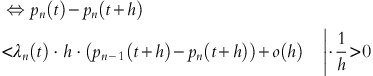
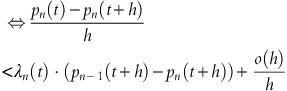
For h→0, this inequality holds if
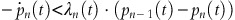 is satisfied; or equivalently
is satisfied; or equivalently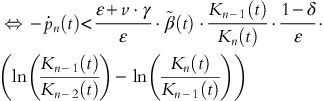
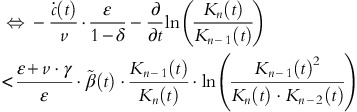
If the unit cost function c(t) is differentiable and not decreasing at time t, the last inequality holds if
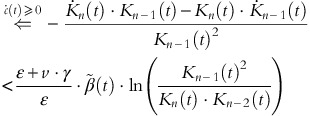
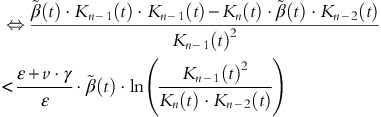
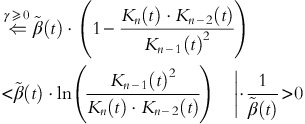
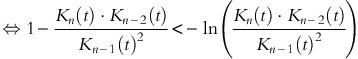
Since K is concave in the inventory level n, we have x≔K n (t)⋅Kn−2(t)/Kn−1(t)2∈(0, 1), and for all 1⩽n⩽N and 0⩽t<T, the last inequality can be expressed as 1−x<−ln x, ∀x∈(0, 1). For x=1, both sides of the inequality are the same, and ∀x∈(0, 1) the right-hand side is decreasing faster in x than the left-hand side, that is, |−1|<|−1/x|. Consequently, ∀x∈(0, 1), the graph of 1−x is strictly dominated by −ln x, and the assertion follows. □
Evaluation and further properties
Proof of computation of simulated revenue and advertising expenditure
For any given (or simulated) sales times, from the definition of the accumulated revenue minus production costs from initial time 0 up to time t, we directly obtain the following formula:

The cumulative advertising expenditure until time t is given by the integrated trajectory of realized (optimal) advertising rates, characterized by given (simulated) sales times τ
j
. The integration of optimal advertising rates  over time from 0 up to t can be set together by the partition of time intervals with the same inventory level:
over time from 0 up to t can be set together by the partition of time intervals with the same inventory level:

Because of the structure of the optimal advertising rates, all single integrals can be explicitly solved, and we obtain a simple sum for the advertising expenditures until time t.
Rights and permissions
About this article
Cite this article
Schlosser, R. A stochastic dynamic pricing and advertising model under risk aversion. J Revenue Pricing Manag 14, 451–468 (2015). https://doi.org/10.1057/rpm.2015.20
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/rpm.2015.20




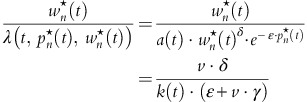
 in the optimality condition for price, that is,
in the optimality condition for price, that is,  , cf. (7), we obtain, d≔ɛ/(v⋅(1−δ)),
, cf. (7), we obtain, d≔ɛ/(v⋅(1−δ)),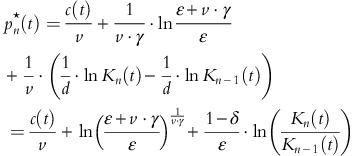
 can be derived by plugging the formula for optimal prices derived above into the optimality condition for optimal advertising rates, cf. (7):
can be derived by plugging the formula for optimal prices derived above into the optimality condition for optimal advertising rates, cf. (7):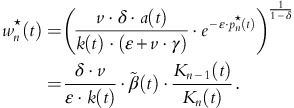
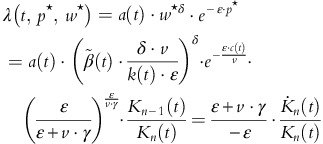
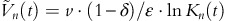 solves
solves 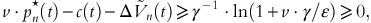
 and
and 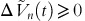 guarantee that p
n
*(t)⩾0 and w
n
*(t)⩾0. Consequently, the optimal controls are admissible. □
guarantee that p
n
*(t)⩾0 and w
n
*(t)⩾0. Consequently, the optimal controls are admissible. □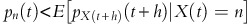
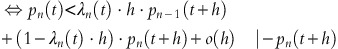
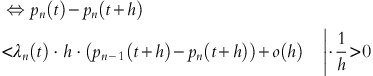
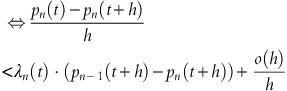
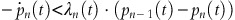 is satisfied; or equivalently
is satisfied; or equivalently