Abstract
The crystal structure, dielectric, magnetic and magnetoelectric (ME) properties of Bi1−xGdxFeO3 (BGFO, x = 0, 0.05, 0.1, 0.15, 0.2) multiferroic ceramics have been studied. The substitution of bismuth by gadolinium induces a
 phase structural transition at x > 0.1, which leads to the suppression of the spiral modulated spin structure and develops weak ferromagnetic properties in the BiFeO3-based materials. Through studying the temperature/magnetic field dependence of the ME coefficient, we have revealed the effect of the substitution of Gd3+ ions on the ME properties, and have demonstrated the possibility of manipulating the electric state in BGFO multiferroics by applying magnetic field at room temperature.
phase structural transition at x > 0.1, which leads to the suppression of the spiral modulated spin structure and develops weak ferromagnetic properties in the BiFeO3-based materials. Through studying the temperature/magnetic field dependence of the ME coefficient, we have revealed the effect of the substitution of Gd3+ ions on the ME properties, and have demonstrated the possibility of manipulating the electric state in BGFO multiferroics by applying magnetic field at room temperature.
Export citation and abstract BibTeX RIS
1. Introduction
Multiferroic materials have attracted great interest not only due to the simultaneous existence of ferroelectricity and magnetism but also possible coupling of their electric and magnetic orderings [1–4], which allows mutual control of the electric polarization with a magnetic field or controlling magnetization by an electric field. This magnetoelectric (ME) effect is potentially important for information storage applications, it would allow magnetic information to be written electrically and to be read magnetically [5–7].
Bismuth ferrite BiFeO3 (BFO) is still the only known multiferroic compound of potential practical interest, which is both antiferromagnetic and ferroelectric with ordering temperatures far above the room temperature (ferroelectric Curie temperature TC of ∼1100 K and an antiferromagnetic Néel temperature TN of ∼640 K). Electrical control of antiferromagnetic domains in BiFeO3 has already been demonstrated in [8–12]. BFO has a rhombohedrally distorted perovskite-type crystal structure with lattice parameters of ahex = 5.571 Å and chex = 13.868 Å at room temperature. The BFO unit cell can be described both in the hexagonal and in the pseudo-cubic form figure 1. The pseudo-cubic representation of these rhombohedral cell parameters is ac = 3.963 Å. The space group is determined as R3c with six formula units per hexagonal unit cell or two formula units per pseudo-cubic unit cell [13]. In this structure, the pseudo-cubic [1 1 1]c is equivalent to hexagonal [0 0 1]h.
Figure 1. Schematic presentation of the BiFeO3 unit cell in the hexagonal and pseudo-cubic settings of R3c space group.
Download figure:
Standard imageSosnowska et al [13] studied the BFO magnetic structure and showed that each Fe3+ spin is surrounded by six antiparallel spins on the nearest Fe neighbours (G-type antiferromagnetism). The exchange interaction between neighbouring Fe magnetic moments within the (0 0 1)h planes is ferromagnetic and antiferromagnetic along [0 0 1]h [13, 14]. The R3c symmetry also permits a canting of the antiferromagnetic sublattice resulting in a weak ferromagnetism if magnetic moments of Fe3+ are oriented perpendicular to the [0 0 1]h axis [15]. Ederer and Spaldin [15] found through the density functional theory calculations that the canting from the collinear direction by an angle of about 1° leads to magnetization of ∼0.1μB per unit cell.
However, the antiferromagnetic spin configuration in BFO is modified by a long-range (620 Å periodicity) modulation leading to a spiral modulated spin structure (SMSS) [13, 14]. This spiral spin structure cancels the macroscopic magnetization and prevents the observation of linear ME effect [14, 16]. Therefore, the evident interest is to suppress this SMSS. It has already been shown that by applying high magnetic field (>18 T) the cycloid spin structure is converted to homogeneous spin order [17, 18]. Destruction of spin cycloid is also reported in strained epitaxial BiFeO3 thin film [10, 19, 20]. Another possible strategy for suppressing SMSS and obtaining spontaneous magnetization in BiFeO3 is the low-level substitution of Bi3+ by rare earth element ions (La3+, Nd3+, Gd3+, Tb3+, Sm3+) [21–24]. In spite of the numerous studies dedicated to doped BFO multiferroic compounds the mechanism, by which ion substitution affects the crystal structure and magnetic properties of BFO, is not completely understood. Moreover, the existing data are contradictory and further research is still required. In this work the Gd3+ (r = 1.053 Å [25]) was chosen as a doping element due to a large difference in ionic radius with respect to that of Bi3+ ions (r = 1.17 Å [25]). Moreover, gadolinium ions are magnetically active and we expect strong magnetic interaction between the Gd3+ ions themselves and between the Gd3+ and Fe3+ ions. Therefore, the variation of the crystal structure upon the cation substitution, as well as dielectric, magnetic and ME properties of Bi1−xGdxFeO3 (BGFO) (x = 0–0.2) multiferroic ceramics, was investigated.
2. Experimental details
The BiFeO3 ceramics were prepared by a solid-state reaction technique using high-purity Bi2O3, Gd2O3 and Fe2O3 oxides taken in a stoichiometric ratio. The mixtures were ground in agate mortar using ethanol as a medium, dried at 80 °C, and calcinated at 750 °C for 4.5 h (heating rate 10 °C min−1). Then the samples were slowly cooled down to room temperature, ground and pressed at 1.5 GPa into pellets 9 mm in diameter and 2 mm in height, and sintered for 10 h. For doped compounds the synthesis temperature was increased from 820 to 900 °C as Gd content increased.
The crystal structure was studied at room temperature by x-ray diffraction (XRD) using a Siemens D 5000 diffractometer with CuKα (α = 1.5418 Å) radiation. Fourier transform infrared (FTIR) spectra were recorded with FTIR spectrometer (Bruker Corporation, Vertex 80V). The magnetization hysteresis (M–H) loops were measured using an automated vibrating sample magnetometer (VSM, Oxford instruments). For the measurements of magnetization as a function of temperature the Physical Property Measurement System equipped with a 9 T superconducting magnet (PPMS: Model 6000, Quantum design) was used. These measurements were carried out by cooling the sample to the desired temperature in the absence (ZFC) or presence (FC) of applied magnetic field. In all these measurements, the cooling and heating rate was kept at 1.5 K per minute and the data were collected every second. For ME measurements all the samples were prepared in the form of parallel-plate capacitor with silver electrodes.
It is worth noting that commercial measurement systems for studying ME effect have not been available so far. In this work the Quantum design PPMS was adjusted to measure ME coefficient. Additionally, an ac magnetic field of Hac = 10 Oe with frequencies from 0.1 to 2 kHz was superimposed onto the dc magnetic field produced by the PPMS-internal superconducting magnet. The ac field was generated by sending an ac current (Keithley 6221) through a coil (1290 turns of AWG 36 phosphor bronze wire, with a diameter of 18 mm) which was assembled on the standard sample puck for PPMS electrical transport measurements. The ME signal was measured by a lock-in amplifier (Stanford research system, Model SR830). Samples were mounted in longitudinal geometry, i.e. ME voltage is parallel to the direction of ac and dc magnetic fields. The ME coefficient was calculated using the relation:
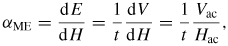
where Vac is the magnetically induced ac electric voltage across the sample, Hac is the amplitude of the ac magnetic field and t is the thickness of the sample.
3. Results and discussion
3.1. Crystal structure
It has been known that single phase BiFeO3 is quite difficult to prepare by the standard solid-state chemistry route. According to the Bi2O3–Fe2O3 phase diagram [26], the kinetics of phase formation can easily lead to the appearance of two impurity phases along with perovskite-structured BiFeO3. Indeed, the high volatility of Bi2O3 leads to the formation of Bi-poor phase Bi2Fe4O9, but a small excess of Bi2O3 in the reactants results in the formation of Bi-rich phase Bi25FeO39.
Figure 2 compares the room temperature XRD patterns of Bi1−xGdxFeO3 samples with x = 0, 0.05, 0.1, 0.15 and 0.2. The major peaks can be readily indexed using the BiFeO3 rhombohedral cell. The presence of non-perovskite Bi2Fe4O9 secondary phase peaks (marked by * in figure 2) was routinely observed in undoped BiFeO3 (figure 1) [27, 28]. These impurity peaks are still present in Bi0.95Gd0.05FeO3. Increase in the Gd content prevents the formation of the second phase and pure phase Bi0.9Gd0.1FeO3 was obtained with all the peaks corresponding to rhombohedral structure with the R3c space group. This supports the idea that doping with a certain amount of Gd stabilizes the perovskite BiFeO3 phase [29].
Figure 2. XRD patterns of Bi1−xGdxFeO3 as a function of x illustrating the clear change in crystal structure at x > 0.1. The lower ticks are given for the BiFeO3 Bragg reflections taken from JCPDS Card No 86-1518. The peaks from the impurity phase Bi2Fe4O9 are marked by *.
Download figure:
Standard imageAnalysis of the XRD patterns (figure 2) reveals that the lattice symmetry gradually changes from rhombohedral (R3c) to orthorhombic (Pnma). It is clear from the two insets of figure 2 that two separate peaks in BFO in the vicinity of 2θ = 40° and 58° are overlapped when Bi atoms are substituted by Gd. Moreover, extra reflections appeared for x > 0.1 which are inconsistent with the R3c symmetry. The Bi1−xGdxFeO3 compounds with x = 0.15 and 0.20 were indexed in an orthorhombic system isostructural to parent orthoferrite (Pnma) GdFeO3 [30]. Rietveld refined crystal structure parameters are listed in table 1. The data confirm the unit cell contraction due to the substitution of smaller Gd3+ ions for the larger Bi3+ ions. The similar phase transformation behaviour and close values of lattice parameters were also observed in the Gd-doped BFO ceramics by Khomchenko et al [31].
Table 1. The refined crystal structure parameters of the Bi1−xGdxFeO3 ceramics.
| Gd content | Space group | a(Å) | b(Å) | c(Å) | V(Å3) |
|---|---|---|---|---|---|
| x = 0 | R3c | 5.576(5) | 13.865(7) | 373.33(3) | |
| x = 0.05 | R3c | 5.572(7) | 13.832(2) | 371.91(4) | |
| x = 0.1 | R3c | 5.564(8) | 13.807(4) | 370.17(4) | |
| x = 0.15 | Pnma | 5.577(2) | 7.900(2) | 5.527(1) | 243.50(2) |
| x = 0.2 | Pnma | 5.624(3) | 7.800(7) | 5.426(5) | 238.02(5) |
3.2. Dielectric properties
Figure 3(a) shows the room temperature FTIR spectra of the BGFO compounds. Reflectivity spectrum consists of an IR-active phonon structure and an electronic background at low frequency. The former is composed of a transverse optical (TO) and a longitudinal optical (LO) mode of the Fe-O oscillations which correspond to the peaks and dips, respectively. Hence, the strong TO phonon peaks near 550 cm−1 and the small one near 435 cm−1 are assigned to the Fe–O stretching and bending vibrations, respectively, being characteristics of the octahedral FeO6 group in the perovskite compounds. The introduction of Gd3+ ions into the BFO parent structure causes an increase in the absolute value of the reflectivity for x < 0.15. It is also seen that larger x leads to broader and stronger peaks with their positions being shifted to lower frequency region. A clear deviation of the FTIR spectra for x > 0.1 from the rest of the samples was also observed in terms of a very broad absorption peak near 547 cm−1, which indicates again the presence of a structural transformation.
Figure 3. IR reflectivity spectra (a); the real ε1(b) and imaginary ε2(c) parts of complex dielectric permittivity obtained through the Kramers–Kronig transformation for Bi1−xGdxFeO3 compounds.
Download figure:
Standard imageThe real ε1 and imaginary ε2 parts of the complex dielectric function ε = ε1 + iε2 of BGFO, derived from the R reflectivity spectra trough Kramers–Kronig transformations, are shown in figures 3(b) and (c). Their features in the infrared region indicate the predominance of the ionic bonding in BGFO compounds and the presence of dielectric polarization mechanisms, related to the elastic displacement of electrons and ions.
In case the external frequency is in the range between the frequencies of the LO and TO phonons, where the real part of dielectric function ε1 is negative, the incident wave experiences a significant reflection (area of the 'metallic reflection') (figure 3).
3.3. Magnetic properties
The dc magnetization curves versus temperature M(T) in a field of 0.2 T are shown in figure 4(a). It should be noticed that the difference in the magnetic moment measured in ZFC and FC sequences is insignificant. All of the curves for Gd-doped BFO show a constant magnetization at high temperatures and a Curie-like upturn below 50 K for the sample with x = 0.05, and below 150 K for the sample with x = 0.2. Figure 4(b) shows the temperature variation of the inverse magnetization below 50 K for Gd-doped compounds. These dependences were found to follow nearly perfectly a Curie–Weiss law. The value of magnetization increases with the increase in the Gd content and no inflexion point can be seen for BGFO. These values and behaviour of magnetization curves for BGFO ceramic samples are consistent with the data reported by Khomchenko et al [31]. However, a clear anomaly in temperature dependence of magnetization for BiFeO3 in the range from about 240 to 270 K can be seen from the inset of figure 3. As has been already mentioned, the secondary phase Bi2Fe4O9 was observed (see figure 1) in BGFO ceramic samples for x below 0.1. This impurity phase is paramagnetic at room temperature and undergoes a transition to an antiferromagnetic state at near TN = 264 K [32]. Therefore, the anomaly in magnetization curve of BFO may be due to the presence of the secondary Bi2Fe4O9 phase. As temperature decreases from 200 to 40 K, the magnetization decreases in accordance with the well-known temperature-dependent magnetization of antiferromagnetics and it shows an increase below 40 K. Similar features in ZFC and FC magnetization curves at low temperatures were reported for single crystals [14, 33] and 245 nm particles of BFO [34]. However, the splitting of ZFC and FC magnetization curves was reported in [33, 34] revealing a spin-glass behaviour at low temperatures. In contrast to that, our ZFC and FC curves for ceramic BFO almost coincide (see the inset of figure 4(a)) thus, possibly, excluding spin-glass transition down to the lowest investigated temperature of 2 K.
Figure 4. (a) Temperature dependence of dc magnetization M(ZFC and FC) under a field of 0.2 T in Bi1−xGdxFeO3 compounds. The inset shows ZFC and FC curves for pure BFO; (b) the inverse magnetization M−1 versus temperature curves (open circles) for Gd-doped BFO with linear curve fitting (black lines).
Download figure:
Standard imageFigures 5(a)–(c) show the magnetization hysteresis M–H loops for BGFO (x = 0–0.2) samples with an applied field up to 8 T. Figure 5(b) presents a zoom of figure 5(a) to highlight the opening-up of the hysteresis loops. For pure BFO, M–H curves exhibit linear field dependence at room temperature with the absence of remanent magnetization (figure 5(c)), as expected for an antiferromagnetic alignment of the Fe3+ magnetic moments. As can be seen from figure 5(b), at 5 K the BFO sample shows a weak ferromagnetism (Mr ≈ 0.002 emu g−1), consistent with the other report [27]. The deviation from linear behaviour appears even at room temperature upon 5% substitution of Bi3+ by Gd3+ ions (see figure 5(c)). The enhancement of magnetic response with increasing Gd content in BGFO compound is more prominent at low temperatures in contrast to room temperature M–H curves which are not saturated at 8 T, thus confirming the basic antiferromagnetic nature of the compound. Indeed, the magnitude of the saturation magnetization at 5 K for the BGFO compounds with x ⩾ 0.1 is an order of magnitude higher than that of BFO (figure 5(a)). It is worth noting that BGFO with x = 0.2 exhibits unusual shape of M–H curves, which is peculiar to orthoferrite Pnma structure [35].The remanent magnetization of BGFO with x = 0.05 and 0.1 achieved at the level around 0.04 emu g−1 and 0.07 emu g−1 at room temperature, respectively, shows an abrupt rise with subsequent increase of Gd (figure 5(d)). It is known that the substitution of Bi3+ ions changes the Fe–O–Fe bond angle, providing the suppression of the spiral SMSS and hence the appearance of weak ferromagnetism [36]. Obviously, at x > 0.1 the gadolinium substitution induces a structural phase transition
 which leads to the collapse of the SMSS and therefore to the noticeable enhancement of magnetization. Moreover, Gd3+ ions with their own large magnetic moments make an important paramagnetic contribution to the net magnetization. Khomchenko et al [37] showed that in Bi0.8(Gd1−xBax)0.2FeO3 system Gd3+ magnetic moments tend to align in the same direction as the weak ferromagnetic component of iron sublattice, thus providing a significant rise to the magnetization.
which leads to the collapse of the SMSS and therefore to the noticeable enhancement of magnetization. Moreover, Gd3+ ions with their own large magnetic moments make an important paramagnetic contribution to the net magnetization. Khomchenko et al [37] showed that in Bi0.8(Gd1−xBax)0.2FeO3 system Gd3+ magnetic moments tend to align in the same direction as the weak ferromagnetic component of iron sublattice, thus providing a significant rise to the magnetization.
Figure 5. (a) and (c) field dependence of magnetization in Bi1−xGdxFeO3 ceramic samples at 5 K and 300 K, respectively; (b) zoomed view of (a); (d) variation of remanent magnetization Mr with Gd content.
Download figure:
Standard imageAnother possibility for interpreting the observed results is to consider the percolation process. The low-level x doping obviously leads to the formation of small isolated magnetic clusters where all spins are parallel. In the composition range 0 < x ⩽ 0.1, the ferromagnetic Fe–Gd clusters are isolated from each other by the Fe–Bi domain. These ferromagnetic mini-clusters grow in size by the substitution of Bi with Gd and in the region of 0.1 < x ⩽ 0.2 (beyond the critical percolation concentration Pc) the ferromagnetic clusters become large enough to be connected with each other, producing macroscopic magnetic moment.
3.4. ME properties
The ME effect is a polarization response to an applied magnetic field, or conversely, the magnetization response to an applied electric field [38]. The ME effect was first theoretically predicted by Landau and Lifshitz for some spin-ordered materials [38] and soon confirmed experimentally by Astrov in antiferromagnetic Cr2O3 [39]. In the presence of magnetic and electric fields the induced polarization in multiferroic materials is obtained from the expansion of the free energy [1]:
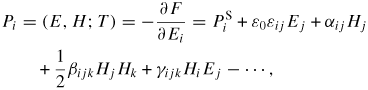
where PS denotes the spontaneous polarization, εij is the relative permittivity. The tensor αij corresponds to induction of polarization by a magnetic field which is described as the linear ME effect. The third rank tensors βijk and γijk are associated with the higher order ME interactions.
Bary'achtar et al [41] predicted that magnetically ordered medium should become electrically polarized near a magnetic inhomogeneity. If the magnetic ordering is inhomogeneous (that is magnetization M varies over the crystal), an electric polarization P arises in the vicinity of this inhomogeneity. The symmetry of the spatial distribution of this polarization is determined by the symmetry of the magnetic inhomogeneity. In the simplest case of cubic symmetry the form of the magnetically induced electric polarization is [42]
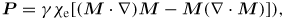
where χe is the dielectric susceptibility in the absence of magnetism.
It was shown by Brown et al [43] that the ME response is limited by the relation
 , where
, where
 and
and
 are the electric and magnetic susceptibilities. Consequently, ferromagnetic ferroelectrics are prime candidates for displaying giant ME effects.
are the electric and magnetic susceptibilities. Consequently, ferromagnetic ferroelectrics are prime candidates for displaying giant ME effects.
The most critical indicator of the ME coupling in multiferroics is the ME coefficient αME. Figure 6(a) presents the temperature dependence of ME coefficient at a fixed frequency f = 0.7 kHz of the ac magnetic field Hac = 10 Oe. With the temperature increasing, the αME gradually increases for all samples and shows a sharp dip around 265 K for BGFO with x < 0.1. The position of the dip is consistent with the temperature of the antiferromagnetic–paramagnetic phase transition in Bi2Fe4O9 impurity phase [32] and coincides with the position of the anomaly in magnetization versus temperature curve for pure BFO (see the inset of figure 4(a)). Our results are in a good agreement with the model proposed by Rado [44]. Using two-sublattice model, it was predicted that as the temperature increases towards the Néel temperature, the longitudinal ME coefficient should increase first to some maximum value and then decrease to zero. This qualitative assumption has been verified experimentally in Cr2O3 by Folen et al [45]. In [44] Rado explained the physical origin of the ME effect as a result of spin–orbit coupling.
Figure 6. ME coefficient αME dependence on temperature (a) and on dc bias magnetic field at room temperature (b) at an ac magnetic field Hac = 10 Oe for BGFO compounds. The inset shows schematic view of the ME measurement circle.
Download figure:
Standard imageThe variation of ME coefficient with dc bias magnetic field at room temperature is shown in figure 6(b). For rhombohedral BGFO compounds with x < 0.15, ME coefficient increases with increasing magnetic field and exhibits maximum around H = 0.3 kOe. These observations are in agreement with those already reported by Caicedo et al for undoped BiFeO3 [2]. In the case of orthorhombic Gd-doped BFO, ME coefficient increases with increasing magnetic field up to 1.2 kOe and attains a maximum value of 9.15 mV cm−1 Oe−1 for x = 0.2. Further increase in magnetic field up to 10 kOe does not bring about any significant variation in the output.
These data present clear evidence for the ME coupling in BGFO ceramic compounds. The observed ME coupling could also be explained through the piezoeffect. In a piezomagnetic BFO [46] an applied magnetic field induces mechanical strain, which, in turn, can induce an electric polarization via piezoelectric effect. It has already been shown that coupling of magnetic and ferroelectric orders in BiFeO3 single crystals [9] and thin films [12] results from the coupling of both antiferromagnetic and ferroelectric domains to underlying ferroelastic domain structure. Application of an electric field reversibly switches ferroelastic domains and is inducing changes in the magnetic structure. So far, the origin of the bulk ME coupling is unclear and further investigations are needed.
4. Conclusion
We have studied crystal structure, dielectric, magnetic and magnetoelectric properties of Bi1−xGdxFeO3(x = 0–0.2) ceramic samples. Analysis of the x-ray powder diffraction patterns showed a continual structural transformation
 , while non-perovskite phase Bi2Fe4O9 disappears completely at x = 0.1. Weak net magnetization in Bi1−xGdxFeO3 develops at low concentrations (5%) of the substituting element. Due to the structural change, the spiral modulated spin structure collapses continuously with increasing Gd content and strongly enhances magnetization and magnetoelectric coefficient at x > 0.1. The Gd-doped BiFeO3 is proved to be magnetoelectric at room temperature, providing an opportunity to control the polarization by the magnetic field as well as the magnetization by the electric field which can be used for developing new types of non-volatile magnetoelectric solid-state memory device. Clearly, this aspect is practically and scientifically very interesting and requires more detailed studies to reveal the origin of magnetoelectric effect in these multiferroic materials.
, while non-perovskite phase Bi2Fe4O9 disappears completely at x = 0.1. Weak net magnetization in Bi1−xGdxFeO3 develops at low concentrations (5%) of the substituting element. Due to the structural change, the spiral modulated spin structure collapses continuously with increasing Gd content and strongly enhances magnetization and magnetoelectric coefficient at x > 0.1. The Gd-doped BiFeO3 is proved to be magnetoelectric at room temperature, providing an opportunity to control the polarization by the magnetic field as well as the magnetization by the electric field which can be used for developing new types of non-volatile magnetoelectric solid-state memory device. Clearly, this aspect is practically and scientifically very interesting and requires more detailed studies to reveal the origin of magnetoelectric effect in these multiferroic materials.
Acknowledgments
The authors acknowledge the financial support from the Belgian Federal Science Policy Office (BELSPO) co-funded by the Marie Curie Actions from the European Commission and from the Methusalem Funding by the Flemish Government.






