Abstract
In this article we review the prospects of laser wakefield accelerators as next generation light sources for applications. This work arose as a result of discussions held at the 2013 Laser Plasma Accelerators Workshop. X-ray phase contrast imaging, x-ray absorption spectroscopy, and nuclear resonance fluorescence are highlighted as potential applications for laser–plasma based light sources. We discuss ongoing and future efforts to improve the properties of radiation from plasma betatron emission and Compton scattering using laser wakefield accelerators for these specific applications.
Export citation and abstract BibTeX RIS
For more information on this article, see LabTalk.
1. Introduction
Bright, high energy photon sources are ubiquitous throughout science but are also used for applications in high energy density physics [1], medicine [2, 3], homeland security [4], industry [5], forensics [6], and even for humanities, such as the probing of great works of art by soft x-rays [7]. New free-electron laser (FEL) x-ray sources with high brightness, such as the Linac Coherent Light Source (LCLS) [8] in the United States of America, the FEL in Hamburg, Germany (FLASH), or SACLA in Japan, are transforming science because of their ability to probe matter to the atomic scale with unprecedented time resolution and brightness compared to synchrotron light sources. Phase contrast imaging is breathing new life into medical imaging by providing more information with lower doses [9, 10]. New research directions for next generation radiation sources include nuclear fluorescence studies [11, 12], and long range detection of special nuclear materials, for example. In the case of many of these advanced sources, the x-rays are generated by the oscillations of energetic electron beams. Within this context, laser wakefield accelerators (LWFAs) [13] may revolutionize energetic photon sources in both size and capability, by providing a compact source of ultra-relativistic electrons for the generation of x- and γ-rays.
The LWFA process is analogous to a surfer being propelled in synchronization with an ocean wave; the electron plasma waves generated by a laser pulse can be used to 'surf' an electron beam to relativistic energies. A plasma is an ionized medium that can sustain electrical fields many orders of magnitude higher than that in conventional radiofrequency accelerator structures [14]. Acceleration of electrons in plasmas, in particular in laser-driven plasmas, has been drawing considerable attention for precisely this reason. LWFA can dramatically reduce the size of accelerators and has the potential to revolutionize the applications in medicine [15] and industry. With the advent of the technique of chirped pulse amplification [16], high-power, short-pulse lasers, have evolved into reliable tabletop devices able to generate intense electromagnetic pulses that can generate extremely large electric field gradients.
Early LWFA experiments included the acceleration of electrons up to a few 100 MeV in the self-modulated laser-wakefield (SMLWF) [17–20], or forced laser wakefield regime [21]. In 2004, three research groups discovered that LWFAs can produce monoenergetic beams of electrons [22–24] which was featured on the cover of Nature. Since then, thousands of papers have been published on this subject in high-impact journals, and energies of more than 1 GeV have now been achieved at several facilities worldwide [25–29], comparable to the electron energies in synchrotron facilities. Developments in fiber laser technology and its use in high-power laser systems should result in orders of magnitude improvement in the repetition-rate of LWFA's over the next decade and make it comparable to that of conventional accelerators [30–32].
A notable application of LWFAs, and the subject of this paper, is the ability to use them as ultra-compact light sources with novel properties. One important mechanism is plasma betatron x-ray radiation, produced when electrons are accelerated in an ultrahigh field gradient in a LWFA and oscillate due to the transverse fields associated with the laser-driven plasma. The theoretical properties of the plasma betatron source are well known [33]; it was first observed in a beam-driven plasma channel [34], and later in the blowout regime of LWFA [35–37]. Since these first observations were made, betatron x-ray generation has been an extremely prolific field of research within the LWFA community. Studies have been carried out at a number of high-intensity laser facilities worldwide and have implied that plasma betatron x-rays have a source size of a few micrometers [37, 38] a divergence of less than 100 mrad [39], a pulse duration of less than 100 fs [40], and a broadband spectrum in the keV energy range [41]. The electron beam emittance and size have been inferred in experiments from the x-ray beam profile [39, 42–44], spectrum [45, 46] or source size [47], using various x-ray spectroscopy and imaging techniques.
Another important mechanism is Compton scattering [48], which occurs when the electron beam impinges on a secondary laser that acts as a wiggler. In addition, a conventional wiggler can be used in tandem with the LWFA electron beam to generate x-rays [49]. The use of an electromagnetic wiggler results in a three orders of magnitude reduction of the spatial size compared to a conventional fixed magnet wiggler. As a result the same x-ray energy can be produced with electron beams of lower energy.
The objective of this paper is not to add to the literature on the physics of such sources but instead to review the capabilities of LWFA-based production of energetic photons for particular applications. In other words, instead of surveying the state of current LWFA-based light source research, we examine what are the requirements of radiation sources for specific applications and how these could potentially be addressed by laser-based sources. This study arose as a result of discussions at the 2013 Laser Plasma Accelerators Workshop.
The structure of the paper is as follows. First we briefly describe the basic physics of LWFA enabled photon sources. Second, we review the state of current and future applications of x- and γ-ray radiation. Finally, we show how LWFA photon sources can address these applications, taking into account brilliance and photon energy requirements, and make recommendations for the field.
2. LWFA energetic photon sources
In this section we give a brief background to laser wakefield acceleration, plasma betatron emission and Compton scattering to provide context for this study. For further information about these topics, the reader is directed to comprehensive reviews of LWFA [14] and radiation emission from LWFAs [36].
2.1. Laser wakefield acceleration
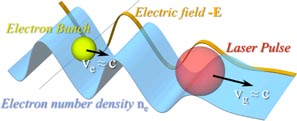
Laser wakefield acceleration is a scheme that uses a high intensity laser pulse propagating through a plasma (figure 1), such that the laser pulse length cτL is shorter than the plasma wavelength (λp = 2πc/ωp, where
 and ne0 is the initial electron number density of the plasma). A relativistic electron plasma wave can be generated by the ponderomotive force (essentially the gradient of the field energy density) of the pulse. This wave is known as a plasma wakefield, and can be used to accelerate trapped electrons with velocities close to the phase velocity of the wave. Trapped electrons, which remain in the accelerating phase of the wave, can reach energies determined by the electric field in the plasma wave and the length over which the acceleration takes place.
and ne0 is the initial electron number density of the plasma). A relativistic electron plasma wave can be generated by the ponderomotive force (essentially the gradient of the field energy density) of the pulse. This wave is known as a plasma wakefield, and can be used to accelerate trapped electrons with velocities close to the phase velocity of the wave. Trapped electrons, which remain in the accelerating phase of the wave, can reach energies determined by the electric field in the plasma wave and the length over which the acceleration takes place.
Figure 1. Principle of laser wakefield acceleration, showing the laser pulse, accelerated electron bunch, and longitudinal electrical field.
Download figure:
Standard image High-resolution imageFor a sufficiently high energy laser pulse, phase matching of an electron beam to the wakefield is maintained over a length known as the dephasing length. Since the laser driver group velocity is less than the speed of light, due to dispersion by the plasma, and the electron beam can approach the speed of light to an arbitrarily small degree as it gains energy, eventually the electron beam will outrun the accelerating fields of the wake. The maximum energy transferred from wake to electron beam is at this distance, and can be estimated by considering the velocity of an electron to be close to the speed of light and the wakefield velocity to be given by the linear group velocity of the laser in plasma,
 , where ω0 is the laser frequency. A more substantial analysis has been given by a mixture of particle-in-cell simulations and scaling laws developed in [50, 51]. By these scalings, the maximum energy gain, that can be realistically expected, scales as
, where ω0 is the laser frequency. A more substantial analysis has been given by a mixture of particle-in-cell simulations and scaling laws developed in [50, 51]. By these scalings, the maximum energy gain, that can be realistically expected, scales as
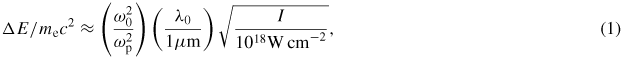
where λ0 is the laser wavelength and I is the focused intensity. It is important to note that this formula assumes a matched spot-size and a matched beam length. For the scalings of Lu et al [51] the pulse duration would be cτFWHM = 2rb/3, the spot-size
 , where rb is the blowout radius, and a0 the laser peak normalized vector potential.
, where rb is the blowout radius, and a0 the laser peak normalized vector potential.
2.2. Betatron radiation
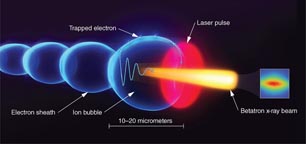
In the three-dimensional (3D), highly non-linear LWFA regime, when a short laser pulse with an intensity I > 1018 W cm−2 is focused inside a plasma, the laser ponderomotive force completely expels the plasma electrons away from the strong intensity regions to form an ion bubble in the wake of the pulse [51]. Electrons trapped at the back of this structure are accelerated and wiggled by the focusing force of the more massive and immobile ions to produce broadband, synchrotron-like radiation in the keV energy range (figure 2). One of the many exciting prospects of LWFA sources is that the electron bunch durations produced in such interactions have been demonstrated to be of fs duration [52, 53]. The radiation pulse generated by the electron beam will have equivalent duration, and hence fs x-ray pulses are likely to be generated by such interactions. This has very exciting implications for time-resolved pump–probe experiments using such laser-generated x-ray pulses.
Figure 2. Principle of betatron x-ray emission from a LWFA. Electrons trapped at the back of the wakefield are subject to transverse and longitudinal electrical forces; they are subsequently accelerated and wiggled to produce broadband, synchrotron-like radiation in the keV energy range.
Download figure:
Standard image High-resolution imageThe spectrum of plasma betatron radiation is characterized by a betatron strength parameter aβ = γkβrβ, where kβ is the wavenumber of the betatron oscillation and rβ is the radius of the oscillation [33, 54]. For aβ ≪ 1, the spectrum is a Doppler shifted peak at 2γ2ωβ corresponding to the betatron frequency ωβ. For aβ ≫ 1, the on axis spectrum is equivalent to the characteristic synchrotron spectrum [33, 55]. In this case the spectrum is broad (synchrotron-like) and extends up to a critical energy,

The average number of photons radiated by a single electron is [33]:

where Nβ is the number of betatron oscillations, and
 is the average harmonic number, which for synchrotron-like emission (large αβ), is
is the average harmonic number, which for synchrotron-like emission (large αβ), is
 . Taking into account the acceleration of the electrons results in a more complicated interaction, but the spectrum is still broadband with a peak energy lower than that predicted by the critical energy corresponding to the highest energy the electrons gain [36, 43, 56].
. Taking into account the acceleration of the electrons results in a more complicated interaction, but the spectrum is still broadband with a peak energy lower than that predicted by the critical energy corresponding to the highest energy the electrons gain [36, 43, 56].
2.3. Compton scattering
Another mechanism for radiation generation is Compton scattering of the electron beam from electromagnetic radiation. An electron, initially at rest, oscillating in a laser field experiencing non-relativistic motion emits radiation at the laser frequency. If the electron is initiated with a relativistic momentum counter-propagating with respect to the laser pulse, then it gains a Doppler upshift. For a very relativistic electron with Lorentz factor γ0, and a lower laser intensity, the upshift in frequency results in emission in a spectral peak at a frequency
 .
.
As the laser intensity increases, the Lorentz force due to the magnetic field begins to become significant, and hence the motion of the electron becomes more complicated. The radiation spectrum starts to pick up higher harmonics of the laser frequency, which gives rise to 'non-linear' Compton scattering. As the intensity increases further, the relativistic motion of the electron in the direction of the laser propagation results in a Doppler-shift of the fundamental frequency, in addition to increasing the spectral power in the harmonics of the down-shifted frequency. For a higher laser intensity, there is a slight down-shift of the up-shifted frequency, as the laser accelerates the electron beam against its motion. However, the normalized laser field strength parameter, a0 = eE0/mecω0, where E0 is the peak electric field, and the normalized betatron (wiggler) parameter, aβ, are almost interchangeable in the description of Compton scattering for a relativistic electron colliding with a laser pulse [57]. Hence, as the strength parameter increases, the photon spectrum tends towards a synchrotron-like broad spectrum, extending to much higher photon energies than the shifted fundamental.
The emission of photons in such processes clearly indicates that a force is applied to the electron to conserve momentum. This radiation force has a classical form, which is self-consistent within the limits that the acceleration timescale is much larger than τ0 = 2e2/3mc3 = 6.3 × 10−23 s [58], which is principally a damping of motion due to loss of momentum to the radiation. One of the interesting phenomena arising from this laser-electron interaction is that the radiation damping is theoretically predicted to be so extreme that for a sufficiently intense laser, the electron beam may lose almost all its energy in the interaction time [59–61]. This means that the radiation force is comparable to the accelerating force, which has the implication that the spectrum of the radiation should be strongly modified.
3. Review of x- and γ-ray applications
This section discusses three specific promising applications of laser–plasma accelerator-based light sources: x-ray phase contrast imaging (XPCI), x-ray absorption spectroscopy, and nuclear resonance fluorescence (NRF). While this list is not intended to be exhaustive, here we describe the basic principles of these applications and discuss ongoing and future efforts to improve them with either betatron radiation or Compton scattering from laser–plasma accelerators.
3.1. X-ray phase contrast imaging
XPCI records the modifications of the phase of an x-ray beam as it passes through a material, as opposed to its amplitude recorded with conventional x-ray radiography techniques. When x-rays pass through matter, elastic scattering causes a phase shift of the wave passing through the object of interest. The cross-section for elastic scattering of x-rays in low-Z elements is usually much greater than for absorption [62]. The total phase shift induced on an x-ray wave when it travels a distance z through a sample with complex index of refraction n = 1 − δ + iβ is due to the real part of the index and calculated with the relation:

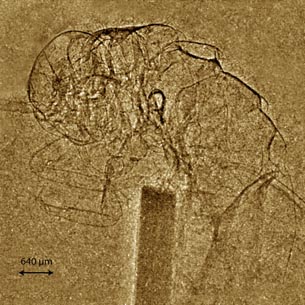
where λ is the x-ray wavelength. For two distinct low-Z elements, the difference in the real part of the complex index of refraction is much larger than the difference in the imaginary part. It means that for quasi transparent objects such as biological samples or tissues, this technique is more sensitive to small density variations, and offers better contrast than conventional radiography. For the past decade, XPCI has been a very active topic of research for medical, biological, and industrial applications. Consequently, several XPCI techniques have been developed based on interferometry [62], gratings [63] and free space propagation [64]. In combination with these techniques, XPCI has been done with various x-ray sources. Examples includes images of a small fish recorded with a standard x-ray tube and gratings [65], images of a bee obtained with a Mo K-alpha laser-based source [66] and phase contrast radiography using x-pinch radiation [67]. Even though, as suggested by equation (4), it is suitable to use a monochromatic x-ray source for XPCI, polychromatic sources with high spatial coherence can also be used [68, 69]. In this case, the scheme is much simpler and does not require using complex and expensive x-ray optics. Much of the sources currently used for XPCI do not have a high temporal resolution desirable to take snapshots of laser-driven shocks or other phenomena. XPCI measurements of shocks done at synchrotrons were limited to a temporal resolution of ∼100 ps [70]; betatron x-ray radiation, where the source size is less than a few micrometers [38], has the potential to offer three orders of magnitude better time resolution. For a source size of 2 µm and a critical energy of 8 keV, the transverse coherence length of betatron radiation was measured at Ltrans = 3 µm 5 cm away from the source, which is sufficient to observe Fresnel diffraction fringes [37]. Using free space propagation techniques, proof-of-principle XPCI measurements of biological samples have recently been done [9, 10] with betatron radiation. These promising results have led to an extension of this technique to higher x-ray energies [71], with an example shown in figure 3.
Figure 3. Single-shot x-ray phase contrast image of a cricket taken using the Astra Gemini Laser. This 200 TW laser produces 1 GeV electron beams and very hard x-rays (with critical energy >30 keV). The image shows minimal absorption, indicative of high flux of photons at energies >20 keV, for which the phase-shift cross-section greatly exceeds (>100×) that for absorption.
Download figure:
Standard image High-resolution imageTo generate a single-shot image, a large photon number is required. As an approximate threshold, a megapixel (1024 × 1024 pixels) is a reasonable number of elements to make an image. The relative fluctuations from Poisson statistics will scale as
 , where
, where
 is the average number of detected photons per pixel. Therefore, for a low noise image the number of photons per shot should be N ≫ 106, assuming the x-rays uniformly fill the detector and are detected. In practice N ≫ 108 is more realistic, given non-uniformities, overfill and detection efficiency. Generally speaking, the ideal source for XPCI should have an average brightness superior than 1012 photons/mm2/mrad2/s/0.1% BW, be monochromatic, and be easily tunable from 10 to 150 keV. For standard medical projection imaging, photon energies in the range 10–30 keV are used for soft tissue absorption radiography such as mammography and 50–150 keV for radiography of hard tissue like bone. Phase contrast imaging is approximately a thousand times more sensitive than absorption contrast, but the advantage over absorption contrast will be more prominent in the hard x-ray region [72]. Although it is not monochromatic, betatron radiation already achieves performances sufficient for XPCI. In order to improve the quality of XPCI experiments with betatron radiation, future directions include a repetition rate increase up to 30 Hz for in vivo imaging [73] and a better field of view, currently limited to <50 mrad. Having a 30 Hz repetition rate allows motion freezing and time lapse imaging of biological phenomena. It corresponds to data acquisition rates of XPCI beam lines at synchrotrons and would allow real-time visualization of internal physiological mechanisms such as the respiration and circulatory systems, or the beating of a heart. One of the applications of XPCI in the medical field is to look at breast cancer. Current systems, as well as synchrotrons and grating-based systems have a field of view of ∼10 cm, whereas current betatron x-ray imaging experiments have a field of view of ∼1 cm, depending on magnification. X-ray microtomography experiments are currently limited to ∼5 µm resolution, which is comparable to what betatron radiation can do. One particular suggested niche area for XPCI with betatron radiation could be ultrafast x-ray imaging with femtosecond resolution [74]. Except XFEL sources, betatron radiation offers the best time resolution ever achieved for XPCI.
is the average number of detected photons per pixel. Therefore, for a low noise image the number of photons per shot should be N ≫ 106, assuming the x-rays uniformly fill the detector and are detected. In practice N ≫ 108 is more realistic, given non-uniformities, overfill and detection efficiency. Generally speaking, the ideal source for XPCI should have an average brightness superior than 1012 photons/mm2/mrad2/s/0.1% BW, be monochromatic, and be easily tunable from 10 to 150 keV. For standard medical projection imaging, photon energies in the range 10–30 keV are used for soft tissue absorption radiography such as mammography and 50–150 keV for radiography of hard tissue like bone. Phase contrast imaging is approximately a thousand times more sensitive than absorption contrast, but the advantage over absorption contrast will be more prominent in the hard x-ray region [72]. Although it is not monochromatic, betatron radiation already achieves performances sufficient for XPCI. In order to improve the quality of XPCI experiments with betatron radiation, future directions include a repetition rate increase up to 30 Hz for in vivo imaging [73] and a better field of view, currently limited to <50 mrad. Having a 30 Hz repetition rate allows motion freezing and time lapse imaging of biological phenomena. It corresponds to data acquisition rates of XPCI beam lines at synchrotrons and would allow real-time visualization of internal physiological mechanisms such as the respiration and circulatory systems, or the beating of a heart. One of the applications of XPCI in the medical field is to look at breast cancer. Current systems, as well as synchrotrons and grating-based systems have a field of view of ∼10 cm, whereas current betatron x-ray imaging experiments have a field of view of ∼1 cm, depending on magnification. X-ray microtomography experiments are currently limited to ∼5 µm resolution, which is comparable to what betatron radiation can do. One particular suggested niche area for XPCI with betatron radiation could be ultrafast x-ray imaging with femtosecond resolution [74]. Except XFEL sources, betatron radiation offers the best time resolution ever achieved for XPCI.
3.2. X-ray absorption spectroscopy
Extremely powerful x-ray absorption techniques, such as extended x-ray absorption fine structure (EXAFS) and x-ray absorption near edge structure (XANES), can reveal electron–ion equilibration mechanisms, when extended to the sub-picosecond time scale [75, 76]. XANES and EXAFS are diagnostic tools providing direct information on valence and core electronic structure, as well as on local atomic order. It is therefore suitable to characterize changes of structures and phase transitions. In standard conditions (no heating, solid density, and room temperature), the absorption spectrum of a material exhibits a sharp edge that reveals the clear separation between occupied and unoccupied states in the conduction band at the Fermi energy. The edge is followed by EXAFS modulations expected from the lattice structures of a solid, which disappear after the heating, indicating a rapid loss of order while the electronic and ionic temperatures increase, and evidencing a fast phase transition. In addition, the broadening of the edge slope reveals the expected broadening of the Fermi level. These techniques have been developed on OMEGA to diagnose iron up to 560 GPa [77], and at LULI-2000 to diagnose Mott nonmetal transitions [78] and to investigate the electronic structure of highly compressed Al [79]. XANES has been used on tabletop systems to characterize the phase transitions of Al up to a few eV [80]. However, these techniques require further development. Models still need improvements to describe in detail the changes in the XANES and EXAFS spectra, mainly because the time resolution of these experiments was intrinsically limited by the x-ray probe duration. Ultrafast x-ray absorption experiments done at the advanced light source synchrotron radiation facility have unraveled the electronic structure of warm dense copper [81], but they required specific slicing techniques to reduce the synchrotron pulse duration that can be realized at the expense of x-ray flux.
Due to its broad, continuous spectrum, femtosecond pulse duration and synchronization with the drive laser, there is wide recognition that betatron radiation has the potential to offer a significant alternative in this domain, but several improvements have to be made to the source in order to achieve this. A typical absorption spectrum of a material exhibits sharp edges, followed by EXAFS oscillations that are generally separated by a few eV and extend up to ∼200 eV after the edge. In general, the oscillation amplitude of the EXAFS signal is on the order of a few % of the total absorption signal (the edge step). Ideally, the random statistical noise,
 , where NPh is the number of x-ray photons in the energy band of interest, should be 1/1000 of the EXAFS signal. This means that the condition NPh > 106 eV−1 must be fulfilled to realize an EXAFS experiment with good statistics. Currently, state-of-the-art betatron radiation sources produce on the order of 108 photons (in the full spectrum) [37], and numbers of 104–105 photons eV−1 have been reported around the 1.56 keV Al K-edge [41]. While these numbers are encouraging, progress needs to be made to improve the source flux and shot-to-shot stability. The source of variation is likely the variation on (i) the electron oscillation amplitude (due to the fact that self-trapping is a highly non-linear mechanism), and (ii) the electron bunch charge, which can be as high as 50% rms. The variation on the oscillation amplitude can be improved by deliberately exciting off-axis [82].
, where NPh is the number of x-ray photons in the energy band of interest, should be 1/1000 of the EXAFS signal. This means that the condition NPh > 106 eV−1 must be fulfilled to realize an EXAFS experiment with good statistics. Currently, state-of-the-art betatron radiation sources produce on the order of 108 photons (in the full spectrum) [37], and numbers of 104–105 photons eV−1 have been reported around the 1.56 keV Al K-edge [41]. While these numbers are encouraging, progress needs to be made to improve the source flux and shot-to-shot stability. The source of variation is likely the variation on (i) the electron oscillation amplitude (due to the fact that self-trapping is a highly non-linear mechanism), and (ii) the electron bunch charge, which can be as high as 50% rms. The variation on the oscillation amplitude can be improved by deliberately exciting off-axis [82].
3.3. Nuclear physics applications
3.3.1. Nuclear resonance fluorescence.
While x-rays interact with the inner-shell electrons of atoms, gamma-rays, on the other hand, interact with the nuclei of atoms and are a powerful tool to reveal isotope-specific properties of certain materials. An application of particular interest is nuclear resonance fluorescence (NRF). NRF is an isotope-specific process, in which a gamma-ray photon with a specific energy (typically a few MeV) is absorbed by a nucleus, which in turns relaxes back to the equilibrium by emitting a photon at slightly lower energy (due to recoil) [83]. Similarly to the fact that K-shell or L-shell fluorescence lines in atoms reveal properties of the spin and oxidation states of a chemical element, NRF lines reveal specific properties of a nucleus, like excitation energies, spin and parities [84]. Since NRF is an isotope-specific process, it can be particularly useful for isotopic assay and detection of materials, an application that spans the domains of non-destructive evaluation, homeland security, nuclear waste assay, stockpile stewardship or mining. The only practical drawback of NRF lines is the fact that their relative spectral width is extremely small (ΔE/E ∼ 10−6). Although it is possible to detect NRF lines with broadband gamma-ray sources produced from bremsstrahlung radiation, it is more desirable to excite them with a narrow-band gamma-ray source. Compton scattering, a process in which laser photons are scattered off a relativistic beam of electrons to produce bright sources of x-rays and gamma-rays, is an ideal candidate to enable efficient NRF detection.
Despite Doppler-broadening, the NRF lines exhibit a relative energy width of ΔE/E ∼ 10−6, which is well below the energy resolution of standard germanium-based detectors. Therefore it is desirable to use a gamma-ray source with a narrow energy linewidth to efficiently excite and detect NRF lines. One could argue that the best solution is to excite the NRF line of a given isotope with the same isotope as the source of exciting radiation. However, recoil energy losses upon emission and absorption prevent us from doing this. Indeed, the recoil yields a shift toward lower energies and the line emitted is off resonance by:

In the case of 7Li, which has an NRF line at 0.478 MeV and a nucleus of atomic weight 7, ΔER = 35 eV. It is larger than the natural linewidth and than the Doppler width (1.33 eV) at room temperature. Within this context, it has been shown that Compton scattering sources produced with a conventional accelerator can efficiently excite NRF lines [11]. As discussed in the next section, the bandwidth of LWFA-based Compton scattering sources is currently on the order of 50%, and therefore not ideal for NRF detection applications.
3.3.2. Other photonuclear reactions.
One of the major concerns of the nuclear medical field where LWFA-based sources could also make a real impact is the lack of availability of medical radioisotopes. There is a present worldwide reluctance of going down the nuclear fission route for energy and the number of reactors that are closing are due in part to a shortage of radioactive isotopes used in a number of applications, including medical ones. This would be a great application of LWFAs if a sufficient flux of gamma-ray photons (at least 1013 photons s−1) with the right energies (1–10 MeV) could be produced. The radioisotopes currently used in nuclear medicine are dictated by availability and cost, but do not necessarily represent the best solution for a given patient. Clinical applications require optimum nuclear and chemical properties. The different γ-induced reactions and the specific radioisotopes that they can produce are discussed in details in [85]. The source required for this application should have a very high average flux (1013–1015 photon s−1), a small diameter (∼100 µm2), and a small relative spectral bandwidth (ΔE/E < 10−3). A significant research effort is currently ongoing to produce LWFA Compton scattering sources [86, 87], but significant improvements in average flux (from ∼108 photons s−1 to 1013 photons s−1) and spectral bandwidth (from 50% down to 1% and less) have to be made for these nuclear physics applications.
4. Requirements of LWFA-based sources for future applications
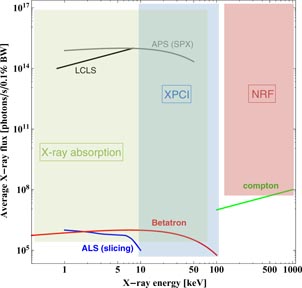
This section summarizes the source needs for the applications proposed in this paper, and gives some directions on how to achieve the desired parameters with laser wakefield-based light sources. A summary plot, showing the desired space-parameters for applications, as well as the current state-of-the-art parameters produced by existing light sources (conventional and laser wakefield-based), is presented in figure 4. Peak brightness, in units of photons/mm2/mrad2/s/0.1% BW, is the unit traditionally used to describe a light source performance. However, applications have different requirements, and it has been agreed upon that, in order to be competitive for applications, LWFA-based sources need to have an increased flux and repetition rate. Hence the metric used in figure 4 is the average x-ray flux, in photons/s/0.1% BW. Recent studies also compare the brightness and flux of betatron radiation with a number of existing light sources [88].
Figure 4. Summary plot, showing the desired space-parameters for XPCI, x-ray absorption and NRF applications. Existing source parameters are also shown for the APS and ALS synchrotrons, the LCLS XFEL, betatron radiation and Compton scattering from LWFAs.
Download figure:
Standard image High-resolution imageTable 1 lists specific parameters for the sources shown in figure 4. For the comparison, we have used the parameters of the APS synchrotron in beamlines where there is a laser pump x-ray probe capability (sectors 7, 11 and 20). Time resolved x-ray absorption spectroscopy experiments are routinely done there [89], as well as XPCI. The beamlines operate within 6–25 keV energies and with ∼1013–1015 x-ray photons s−1 available [90, 91]. The real advantage of synchrotrons is their ability to execute laser-pump x-ray probe experiments at a MHz repetition rate [92, 93]. Their only drawback is the few picoseconds time resolution they offer, which is about three orders of magnitude superior to transient phenomena that occur at the atomic level. On the other hand, XFELs offer a femtosecond time resolution and the brightest light source ever produced, which has enabled several seminal experiments in various domains of physics, chemistry and biology [94–99]. XFELs are currently limited to a 120 Hz repetition rate and to photon energies around 25 keV (in the third harmonic). One of their drawbacks is the shot-to-shot reproducibility of the spectrum. XFELs operating in the self-amplified spontaneous emission (SASE) mode have poor temporal coherence and large statistical fluctuations, because SASE FEL emission begins with the random shot noise in the electron beam. To improve this, various seeding techniques are being investigated [100]. While its flux and transverse coherence make it an excellent candidate for ultrafast XPCI experiments [101], an XFEL is not the ideal source for x-ray absorption spectroscopy, in part because its narrow spectrum (a few eV) does not span the full XANES and EXAFS regions (on the order of 200 eV wide).
Table 1. Relevant source parameters for the APS and ALS (slicing mode) synchrotrons, the LCLS XFEL, betatron radiation and Compton scattering from current LWFA experiments.
| Parameter | APS | ALS | LCLS | Betatron | Compton |
|---|---|---|---|---|---|
| Pulse duration | 20–100 ps | <1 ps | 10–80 fs | 30–60 fs | 30–60 fs |
| Repetition rate | 6.5 MHz | kHz | 120 Hz | 1 Hz | 1 Hz |
| Energy range | 0.2–40 keV | 0.25–9 keV | 0.5–24 keV | 1–80 keV | 0.1–2 MeV |
| Bandwidth | 2–100% | 100% | 0.1% | 100% | 50% |
| Tunability | Variable undulator gap | Limited | e-beam energy | e-beam energy | e-beam energy |
| Photons/pulse | 108 | 107 | 1013 | 108 | 107 |
| Reproducibility | Excellent | Excellent | Limited (SASE) | Poor | Poor |
While both synchrotrons and XFELs have limitations to execute a number of applications, their size and cost is mainly what limits their development worldwide. In order to offer a viable alternative to these sources with LWFA, several improvements need to be made. Source parameters presented in table 1 were taken from recent reports on betatron radiation [37, 43] and Compton scattering [86, 87, 102] from LWFAs. From figure 4 and table 1, many of the betatron radiation and Compton scattering source parameters are still marginal to be truly competitive with XFELs and synchrotrons. Proof-of-principle experiments can be (and have been done) with good success for XPCI, but parameters such as x-ray flux and x-ray source repetition rate will have to be enhanced for efficient x-ray absorption spectroscopy experiments.
Table 2 summarizes the improvements that need to be made on betatron radiation and Compton scattering sources. Most importantly, their shot-to-shot reproducibility needs to be improved. This problem is due to the highly non-linear nature of the blowout regime of laser-wakefield acceleration and its sensitivity to nonideal laser beam and plasma density profiles [103]. In experiments, electron beam spectra with less than 10% energy spreads have been reported presenting fluctuations between 1–10 MeV per shot. Several methods to control the stability and injection of electron beams have been proposed and some of them demonstrated experimentally. These include colliding-pulse injection [104, 105], density gradient injection [106, 107], inner-shell ionization-induced trapping [108–110], cold injection [111], and transverse control of self-injection using counter-propagating lasers [112] or external magnetic fields [113]. For the case of colliding-pulse injection, it yields more controllable betatron radiation [114]. In the near term, betatron radiation and Compton scattering should be produced and observed in these experimental conditions to understand if the methods to control the injection and stability of the electron beams have an effect on the light sources output reproducibility. Other betatron source parameters, such as polarization, can also be controlled by tailoring the laser intensity profile and pulse front tilt [115, 116].
Table 2. Desired betatron and Compton scattering x-ray source parameters for applications.
| Parameter | Betatron | Compton | How it can be improved |
|---|---|---|---|
| Repetition rate | >30 Hz | >30 Hz | Fiber or higher repetition rate laser |
| Energy range | 1–150 keV | 1–10 MeV | Higher energy electron beams |
| Bandwidth | 100% | <1% | <1 mm mrad emittance and <1% energy spread e-beams |
| Photons/second | 108 | 1013 | Increase in repetition rate |
| Jitter | 1% rms | 1% rms | Controlled injection schemes |
In order to reach gamma-ray energies, Compton scattering is a better choice than betatron radiation. Betatron x-rays with spectra peaking at 150 keV and containing ∼108 photons have been reported [117], due to the interaction of the electron bunch with the laser [118], but the Compton scattering mechanism naturally offers better tunability by varying the electron beam energy [102]. For NRF studies, Compton scattering sources from LWFA are currently too broad (on the order of 50% full width at half maximum). Although NRF signatures have been successfully detected with broadband bremsstrahlung sources before [119], any photons with energies outside of the resonance will contribute to a poor signal-to-noise ratio [120], and it has taken up to several hours to detect NRF in 7Li using a Compton scattering source based on a linear accelerator and with a relative bandwidth of ∼15% [11]. Therefore, until gamma-rays with a narrower bandwidth are produced, current LWFA-based Compton scattering sources seem more suited for photofission [121], exciting giant dipole resonances [122], and selective activation of nuclear materials [123]. Other noteworthy applications of LWFA-based Compton scattering sources can include nuclear lifetime measurements by streaking, nuclear spectroscopy and pump–probe experiments [124].
Finally, the average flux, and consequently the repetition rate and the number of x-ray photons per pulse, need to be improved for both betatron radiation and Compton scattering LWFA-based sources. Although the number of x-ray photons per pulse is comparable to that from synchrotrons, the repetition rate of LWFA-based light sources is currently limited to 1–10 Hz by the Ti : Sapphire drive lasers. Novel laser technologies, which can support kHz repetition rates and kW average powers with a ∼20% wall-plug efficiency, need to be developed for LWFA experiments. This requires several technological advancements in coherent combination of fibers, advanced solid state laser gain materials, high damage threshold materials and gratings, diode lasers, and high power CPA techniques. Excellent laser beam quality and stability should also be achieved. Some efforts are beginning in the US to develop these technologies [125]. There is also a large effort in Europe known as ICAN (International Coherent Amplification Network) in beam combination of short pulse fiber lasers.
5. Conclusion
We have introduced several examples of applications of laser wakefield accelerator-based light sources. We have emphasized applications such as x-ray phase contrast imaging, x-ray absorption spectroscopy, which are both routinely done at synchrotron facilities. Nuclear physics with gamma-ray beams, traditionally produced from conventional accelerators, could also benefit from advances in LWFA-driven Compton scattering sources. Laser-driven sources have the potential to be genuinely compact and relatively inexpensive, particularly with the possibility of high repetition-rate fiber laser technology around the corner. If the research community works on reducing the shot-to-shot jitter of the spectrum and the flux to a few percent, while improving the photon flux by two orders of magnitude and more, applications will become a reality.
Acknowledgments
The authors acknowledge discussions with all the participants of the 2013 Laser Plasma Accelerators Workshop. The conference was supported by the John Adams Institute for Accelerator Science (STFC grant ST/J002062/1). Part of this work was performed under the auspices of the US Department of Energy under contract DE-AC52-07NA27344 at LLNL and supported by the Laboratory Directed Research and Development (LDRD) Program under tracking code 13-LW-076. AGRT acknowledges funding from NSF CAREER under grant 1054164.