Abstract
First-principles calculations are performed to obtain the dielectric function and loss spectra of bulk PdHx. Hydrogen concentrations between x = 0 and 1 are considered. The calculated spectra are dominated by a broad peak that redshifts in energy with x. The obtained bulk dielectric function is employed to compute the loss spectra of PdHx spherical nanoparticles as a function of x. The dominant plasmon peak in the spherical nanoparticle is lowered in energy with respect to the bulk case. However, the dependence of the resonance energy on the hydrogen concentration is roughly similar to that in bulk.
Export citation and abstract BibTeX RIS
1. Introduction
Collective electronic excitations—plasmons—play a key role in a vast number of phenomena and have been intensively studied for decades. In particular, great effort has been devoted recently to the investigation of localized surface plasmons (LSPs) in metallic nanoparticles. LSPs are collective excitations of the valence band electrons, similar to conventional surface plasmons in extended systems [1, 2]. The energy of LSPs depends on the particle size, shape, dielectric properties and temperature, as well as on the optical properties of the environment [3, 4]. The optical response of metal nanostructures such as nanoshells [5, 6], nanodisks [7, 8], nanorings [9, 10] and others is governed by an LSP peak, red-shifted in energy with respect to the bulk plasmon. The properties of LSPs can be tuned over an extended wavelength range and many applications based on LSPs have thus been developed, including ultrasensitive chemical sensing [11, 12], biomedical activity [13, 14] and photovoltaic devices [15].
Recently, LSPs have been successfully used to monitor the changes in the crystalline structure of Pd nanoparticles upon H absorption [8]. Bulk and nanoparticle metal hydrides have been extensively studied due to their importance in many applications such as hydrogen storage [16–21]. The novel scheme [8] is based on the modification of the optical properties of nanoparticles, i.e. the shift in energy of the LSP peak, during the H absorption process. This direct nanoplasmonic sensing technique is highly promising but quantitative measurement of the H absorbed in the nanoparticle requires an accurate conversion of the LSP energy shift to H concentration. Although a linear dependence of the LSP response of palladium on hydrogen uptake used in [8] seems well grounded [10], there is no theoretical support for its validity. In this respect, a key question is how the dielectric properties of a PdHx system evolve with variation of x. The goal of the present paper is to provide new insight into this problem based on first-principles calculations of the electron energy-loss spectra of PdHx, for bulk and nanoscale systems.
Palladium can easily absorb hydrogen through several elementary steps, namely, H2 molecular dissociation at the surface, diffusion of H atoms into the lattice, and localization at interstitial sites. In bulk, the influence of H absorption on the Pd electronic structure has been thoroughly analyzed [22–26]. Hydrogen absorption reduces the width of the Pd valence d-band and induces new electronic states at energies just below the bottom of the band. Increasing the H concentration in PdHx results also in a strong reduction of the density of states at the Fermi level for x ≥ 0.6. Concerning the influence of these changes in PdHx optical properties, EELS measurements show that the dominant bulk plasmon energy is gradually shifted from ∼7 eV in clean Pd to ∼5 eV in PdH0.7 [25]. This strong shift cannot be explained in terms of a simple free-electron-gas picture. Interband transitions from occupied Pd d-bands to unoccupied H-modified sp states come into play, as shown by recent ab initio calculations for Pd and PdH [27]. Nevertheless, a detailed theoretical investigation, based on first principles, of the evolution of PdHx dielectric properties as a function of the hydrogen concentration x is, to the best of our knowledge, still lacking.
Here we use first-principles calculations to obtain the dielectric function and loss spectra of bulk PdHx for hydrogen concentrations between x = 0 and 1. We show that the spectra are dominated by a broad peak that redshifts quite smoothly with x. In order to analyze the effects that finite size and confinement produce in the collective electron excitations of PdHx, the bulk dielectric function is then employed to compute the loss spectra of PdHx spherical nanoparticles as a function of x. We show that the dominant plasmon peak in the spherical nanoparticle is lowered in energy with respect to the bulk case, although not as much as one may expect from a simple classical Drude-like description of the LSP. The dependence of the LSP resonance energy on the hydrogen concentration is roughly similar to that in bulk.
2. Theory
Technical details of the first-principles calculations are similar to those used for Pd and PdH in [27] and are only briefly summarized here. Density functional theory (DFT) is used to obtain the ground state of bulk PdHx for different values of x. For pure face-centered cubic (fcc) Pd, the experimental lattice parameter aPd = 7.35 au is used. For PdH, the Pd atoms form an fcc lattice and the H atoms occupy all octahedral interstitial sites. The value aPdH = 7.79 au is used as in [24]. For other values of x in PdHx, the H atoms are placed at octahedral interstitial sites of the lattice, keeping periodicity and a proper stoichiometry in the compound. The lattice parameter is then varied self-consistently. A random distribution of H atoms over the interstitial sites of the lattice would introduce additional broadening of some features of the excitation spectrum but no qualitative changes are expected [28].
In the framework of time-dependent density functional theory (TDDFT) [29] and within linear response, the Fourier coefficients of the density-response function of the system χG,G'(q,ω) can be obtained through the following integral equation:
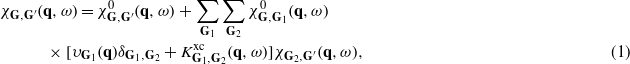
where all Gs are the reciprocal lattice vectors, υG1 is the bare Coulomb potential,  accounts for dynamical exchange–correlation effects, and
accounts for dynamical exchange–correlation effects, and  are the Fourier coefficients of the density-response function for a noninteracting electron system built from the DFT Kohn–Sham energies εnk and wavefunctions ψnk. The imaginary part of the matrix
are the Fourier coefficients of the density-response function for a noninteracting electron system built from the DFT Kohn–Sham energies εnk and wavefunctions ψnk. The imaginary part of the matrix  can be evaluated [30] with the use of a spectral function matrix according to the expression
can be evaluated [30] with the use of a spectral function matrix according to the expression
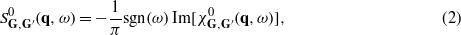
where  is defined as
is defined as
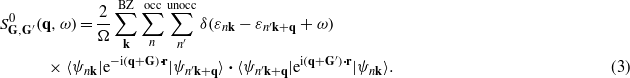
Here n, n' are band indices, the wavevectors k and q are in the first Brillouin zone (BZ), the factor 2 accounts for the spin, and Ω is the normalization volume.
The Fourier coefficients of the electron energy-loss function ![$\mathrm{Im}[{\epsilon }_{\mathbf{G}=0,\mathbf{G}^{\prime}=0}^{-1}(\mathbf{q},\omega )]\equiv \mathrm{Im}[{\epsilon }^{-1}(\mathbf{q},\omega )]$](https://content.cld.iop.org/journals/0953-8984/24/10/104021/revision1/cm403022ieqn31.gif) for momentum transfer q and energy ħω can then be obtained from those of χG,G'(q,ω) through
for momentum transfer q and energy ħω can then be obtained from those of χG,G'(q,ω) through
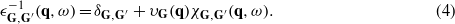
For our calculation of the excitation spectra, we perform a full inversion of the matrix χG,G'(q,ω) (see equation (1)), with up to 50 values of G and G' considered. Nevertheless, we have checked that local field effects [31] are minor in the range of energies considered although some effect at higher energies is observed in agreement with previous work [32]. We have performed calculations of the density-response function for interacting electrons, χ, using equation (1) for two kinds of the exchange–correlation kernel Kxc, namely within a random-phase approximation (RPA) when Kxc = 0 and an adiabatic local density approximation (ALDA) with
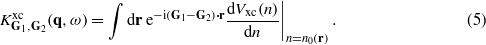
Here Vxc(n) is the exchange–correlation potential of a homogeneous electron gas of density n and n0(r) is the self-consistent valence electron density at spatial coordinate r. Comparison of these two sets of data have verified that they are almost identical in the reported energy region, i.e. the dynamical exchange–correlation effects beyond the RPA play a minor role in the studied systems like in other d metals [33].
3. Results and discussion
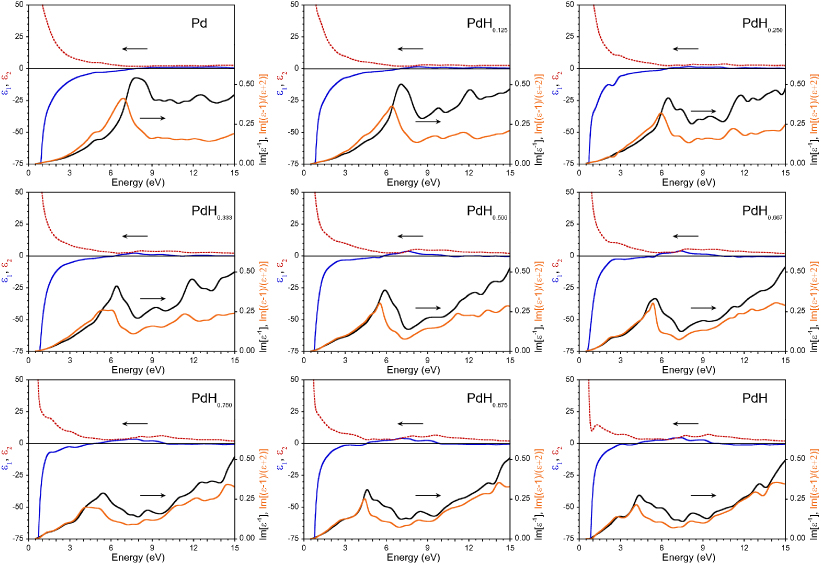
In figure 1 we plot the real  1 and imaginary
1 and imaginary  2 parts of the dielectric function
2 parts of the dielectric function  =
=  1 + i
1 + i 2, as well as the electron energy-loss function Im[
2, as well as the electron energy-loss function Im[ −1], for q with q → 0, i.e. in a range relevant for optical properties, for several values of x in bulk PdHx as a function of energy ω. The profile of Im[
−1], for q with q → 0, i.e. in a range relevant for optical properties, for several values of x in bulk PdHx as a function of energy ω. The profile of Im[ −1] is dominated by a broad feature whose energy smoothly shifts from ωP ≈ 7.7 eV for x = 0 to ωP ≈ 4.3 eV for x = 1. This peak is commonly attributed to the bulk plasmon although interband electron–hole pair transitions contribute to the weight as well [27]. Increasing the concentration of H in bulk PdHx shrinks the energy of the plasmon peak and reduces its weight, due to the reduction in the density of states at the Fermi level and the increasing importance of interband electron–hole pair transitions.
−1] is dominated by a broad feature whose energy smoothly shifts from ωP ≈ 7.7 eV for x = 0 to ωP ≈ 4.3 eV for x = 1. This peak is commonly attributed to the bulk plasmon although interband electron–hole pair transitions contribute to the weight as well [27]. Increasing the concentration of H in bulk PdHx shrinks the energy of the plasmon peak and reduces its weight, due to the reduction in the density of states at the Fermi level and the increasing importance of interband electron–hole pair transitions.
Figure 1. Set of panels containing real (solid blue line) and imaginary (dotted red line) parts (top part of each panel) of the dielectric function  =
=  1 + i
1 + i 2 of bulk PdHx for different values of x, as a function of the energy ω (in eV). The bottom part of each panel shows the bulk loss function Im(
2 of bulk PdHx for different values of x, as a function of the energy ω (in eV). The bottom part of each panel shows the bulk loss function Im( −1) (thick black line) and the particle absorption spectra (thin orange line) for the same systems.
−1) (thick black line) and the particle absorption spectra (thin orange line) for the same systems.
Download figure:
Standard imageThe previous analysis refers to bulk. Similar influence of the H absorption on the position of the LSP peak can be found in finite nanosystems. In order to include finite size effects in a simplified way, we consider the polarizability α of a spherical particle in vacuum in the Rayleigh limit, for which the absorption spectrum is proportional to Im[α] ∝ Im[( − 1)/(
− 1)/( + 2)]. This approximation, in which size effects are neglected, should remain valid as long as the wavelength of the external field is much larger than the nanoparticle size. We introduce our bulk-calculated ab
initio
+ 2)]. This approximation, in which size effects are neglected, should remain valid as long as the wavelength of the external field is much larger than the nanoparticle size. We introduce our bulk-calculated ab
initio  into this expression to obtain the absorption spectrum of PdHx spherical nanoparticles. Figure 1 shows the evolution of these characteristics for different values of x as a function of the excitation energy. The qualitative behavior of the LSP peak with x is similar to that in bulk, although the resonance energy is shifted to slightly lower values.
into this expression to obtain the absorption spectrum of PdHx spherical nanoparticles. Figure 1 shows the evolution of these characteristics for different values of x as a function of the excitation energy. The qualitative behavior of the LSP peak with x is similar to that in bulk, although the resonance energy is shifted to slightly lower values.
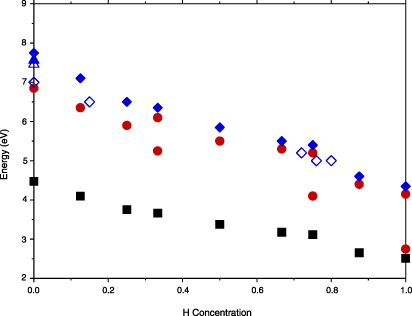
The redshift of the LSP energy due to the finite size of the PdHx nanoparticles can be quantified with the help of figure 2, in which the plasmon peak position in bulk ωP and spherical nanoparticles ωLSP is plotted as a function of the absorbed H concentration. Experimental results for the plasmon position in bulk PdHx materials [25, 34, 35] are shown in figure 2 as well. Note that, in figure 1, the dominant peak in the particle absorption spectra has a strongly non-Lorentzian shape for x = 0.333 and 0.750. For this reason, we have fitted this peak with two Lorentzians and the corresponding energy values are presented in figure 2. Also we highlight the energy position of a prominent shoulder around 2.75 eV at x = 1. In general, a monotonous decrease of both ωP and ωLSP upon increase of the H concentration x is found, with a notable drop at x ≈ 0.75. At this value of x, the d-band becomes totally occupied and falls below the Fermi level. The Fermi surface is then mostly of sp-character and the weight of intraband transitions at the Fermi level in the excitation spectrum is drastically reduced [36–38].
Figure 2. Energy (in eV) of calculated LSR ωLSP in PdHx spherical nanoparticles as a function of hydrogen concentration x (circles). The plasmon peak positions in the bulk case ωP (diamonds) and the Drude-like plasmon peak positions  in spherical nanoparticles (squares) are shown as well. The open diamonds, open triangle, and filled triangles present bulk plasmon energy values measured in [25], [34], and [35], respectively.
in spherical nanoparticles (squares) are shown as well. The open diamonds, open triangle, and filled triangles present bulk plasmon energy values measured in [25], [34], and [35], respectively.
Download figure:
Standard imageThe results in figure 2 are also compared with those extracted from a simplified Drude-like description of the nanoparticle dielectric function  D, in which the plasmon energy is approximated by
D, in which the plasmon energy is approximated by  . The difference between the values of ωLSP and
. The difference between the values of ωLSP and  proves that the optical absorption properties of PdHx nanoparticles cannot be estimated from free-electron-like arguments. Electronic structure effects bring about distinct changes in the absorption spectra.
proves that the optical absorption properties of PdHx nanoparticles cannot be estimated from free-electron-like arguments. Electronic structure effects bring about distinct changes in the absorption spectra.
Qualitatively, the plasmon energy shift in PdHx is consistent with existing experimental information. The energy of LSP peaks in pure Pd nanodisks ranges between roughly 1 and 2.5 eV depending on the disk diameter [7]. Exposure to hydrogen shifts the LSP absorption peak to lower energies in nanodisks [8]. Pd and PdH nanorings show resonance peaks at similar low energies [10]. Detailed calculations of the electronic response for particular sizes and shapes of PdHx nanosystems would then be necessary to perform a more quantitative comparison of the dependence of LSP absorption peaks on H concentration.
4. Conclusions
In summary, we have presented a basic ingredient for the evaluation of the optical properties of PdHx nanoparticles—the corresponding dielectric function—for H concentrations ranging from x = 0 to 1. Our first-principles calculations of the dielectric properties of PdHx systems show how the modifications in the electronic structure of PdHx with H concentration are reflected in the absorption spectra. In particular, the plasmon energy in bulk (nanoparticle) PdHx is a decreasing function upon increase of H concentration x and red-shifted roughly ≈3.5 eV (≈2.5 eV) from x = 0 to 1.
Our findings demonstrate the importance of this kind of calculation in determining the dielectric properties of non-free-electron-like metal systems such as PdHx. In addition, ab initio results of the dielectric function are ready to be used as valuable input for subsequent semiclassical calculations of the optical response [9, 39]. The latter can take into account size, shape and chemical environment effects. The combination of both methodologies is thus a powerful tool to accurately obtain from purely theoretical grounds the electromagnetic response of finite systems in the nanoscale.
Acknowledgments
This work was supported in part by the Basque Departamento de Educación, Universidades e Investigación (grant No. IT-366-07), the Basque Departamento de Industria through the ETORTEK project, and the Spanish Ministerio de Ciencia e Innovación (grant No. FIS2010-19609-C02-00).