Abstract
We discuss the use of nonlocal impedance conditions within the use of boundary integral equations for the solution of direct and inverse obstacle scattering problems for penetrable obstacles with constant index of refraction. In the first part, for the classical transmission problem we present an approach that leads to a two-by-two system of nonlinear integral equations in the spirit of the method initiated by Kress and Rundell (2005 Inverse Problems 21 1207–23) rather than the three-by-three system arising from the traditional boundary integral equation approach to the transmission conditions. In the second part we survey on recent work of Cakoni and Kress (2017 Appl. Anal. 96 23–38) on the use of boundary integral equations for the characterization and numerical computation of transmission eigenvalues. In particular, we modify and simplify the analysis by the use of a nonlocal rather than a local impedance condition as in the 2017 paper.
Export citation and abstract BibTeX RIS
1. Introduction
Scattering from a sound-soft or a sound-hard obstacle provides the two basic classical scattering problems for time-harmonic acoustic waves. Assume an impenetrable obstacle described by a bounded domain  with a connected
with a connected 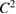 smooth boundary
smooth boundary  and an incident field given by the plane wave
and an incident field given by the plane wave 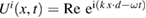 where
where 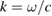 is the wave number,
is the wave number, 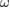 the frequency,
the frequency,  the speed of sound, and
the speed of sound, and
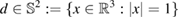
the direction of propagation. Then, setting 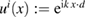 , the two basic problems are to find the total field
, the two basic problems are to find the total field  as a solution to the Helmholtz equation
as a solution to the Helmholtz equation

such that the scattered wave 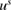 satisfies the Sommerfeld radiation condition
satisfies the Sommerfeld radiation condition

uniformly for all directions. Solutions to the Helmholtz equation satisfying the Sommerfeld radiation condition are called radiating solutions. The boundary conditions are given by the homogeneous Dirichlet condition

in the sound-soft case and the homogeneous Neumann condition

in the sound-hard case, with  the unit normal to
the unit normal to  directed into
directed into 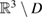 .
.
After renaming the unknown functions the two scattering problems are special cases of the following exterior Dirichlet and Neumann boundary value problems: Find a radiating solution  to the Helmholtz equation satisfying
to the Helmholtz equation satisfying

or

with given 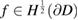 for the Dirichlet case and
for the Dirichlet case and  for the Neumann case, respectively.
for the Neumann case, respectively.
In addition to these two standard boundary conditions, so called impedance boundary conditions were introduced mainly to model scattering problems for penetrable obstacles approximately by scattering problems for impenetrable obstacles. The classical impedance condition, also known as Leontovich condition, is given by

where  is a given complex valued function with non-negative real part. The generalized impedance boundary condition is described by
is a given complex valued function with non-negative real part. The generalized impedance boundary condition is described by
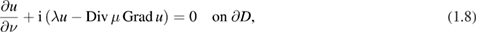
where 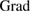 and
and 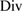 denote the surface gradient and surface divergence on
denote the surface gradient and surface divergence on  and
and 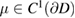 and
and 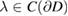 are given complex valued functions with non-negative real parts. As compared with the Leontovich condition, the wider class of impedance conditions (1.8) can provide more accurate models, for example, for imperfectly conducting or coated obstacles.
are given complex valued functions with non-negative real parts. As compared with the Leontovich condition, the wider class of impedance conditions (1.8) can provide more accurate models, for example, for imperfectly conducting or coated obstacles.
The above impedance conditions (1.7) and (1.8) are local conditions whereas in this survey we want to discuss nonlocal impedance conditions of the form

for solutions  to the Helmholtz equation defined either in
to the Helmholtz equation defined either in 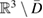 or in
or in  . Here, at least one of the two operators
. Here, at least one of the two operators 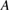 and
and 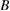 will contain integral operators, or more general pseudo differential operators defined in Sobolev trace spaces on
will contain integral operators, or more general pseudo differential operators defined in Sobolev trace spaces on 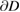 . These nonlocal impedance conditions have no immediate physical interpretation and only serve as an analytic tool for the investigation of mathematical problems related to direct and inverse obstacle scattering.
. These nonlocal impedance conditions have no immediate physical interpretation and only serve as an analytic tool for the investigation of mathematical problems related to direct and inverse obstacle scattering.
The plan of the paper is as follows. We begin in section 2 by indicating that the classical suggestion by Panich [24] to overcome the non-uniqueness issue of the single-layer potential approach for solving the exterior Neumann problem (1.6) can be interpreted as an application of a nonlocal impedance condition for the interior domain  . In the following section 3 we illustrate the use of the same type of interior impedance problem to formulate a solution method for the scattering problem from a penetrable scatterer
. In the following section 3 we illustrate the use of the same type of interior impedance problem to formulate a solution method for the scattering problem from a penetrable scatterer 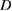 with constant refractive index by one single boundary integral equation for one unknown instead of the classical approach with two equations for two unknowns. Complemented by a far field equation, in the spirit of the method proposed by Kress and Rundell [17], this new integral equation creates a system of two nonlinear equations for solving the inverse scattering problem to determine the shape of the scatterer from a known far field pattern. A couple of numerical examples is presented as proof of concept for this method. This is then followed in section 4 by a brief description of the same idea for scattering from an extended source with constant density. The final section 5 reviews recent work of Cakoni and Kress [5] employing boundary integral equations and using impedance conditions for the characterization and numerical computation for transmission eigenvalues for penetrable obstacles with constant refractive index. This research was motivated by the work of Cossonnière and Haddar [9] who presented a two-by-two system of integral equations based on Green's representation theorem for the interior transmission problem whereas in [5] again a single boundary integral equation was derived. In the present, we eliminate some negligence within the presentation in [5] and simplify the analysis by the use of a nonlocal rather than a local impedance condition. Although, except the numerical examples, our presentation will be in
with constant refractive index by one single boundary integral equation for one unknown instead of the classical approach with two equations for two unknowns. Complemented by a far field equation, in the spirit of the method proposed by Kress and Rundell [17], this new integral equation creates a system of two nonlinear equations for solving the inverse scattering problem to determine the shape of the scatterer from a known far field pattern. A couple of numerical examples is presented as proof of concept for this method. This is then followed in section 4 by a brief description of the same idea for scattering from an extended source with constant density. The final section 5 reviews recent work of Cakoni and Kress [5] employing boundary integral equations and using impedance conditions for the characterization and numerical computation for transmission eigenvalues for penetrable obstacles with constant refractive index. This research was motivated by the work of Cossonnière and Haddar [9] who presented a two-by-two system of integral equations based on Green's representation theorem for the interior transmission problem whereas in [5] again a single boundary integral equation was derived. In the present, we eliminate some negligence within the presentation in [5] and simplify the analysis by the use of a nonlocal rather than a local impedance condition. Although, except the numerical examples, our presentation will be in  , we note that all our results remain valid in
, we note that all our results remain valid in 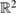 with some slight modifications.
with some slight modifications.
2. An early occurrence in history
Following the notation of [8, section 3.1], in terms of the fundamental solution
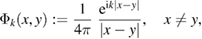
to the Helmholtz equation in  we introduce the classical boundary integral operators given by the single- and double-layer operators
we introduce the classical boundary integral operators given by the single- and double-layer operators
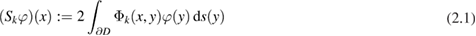
and
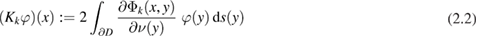
and the corresponding normal derivative operators
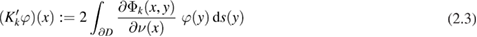
and
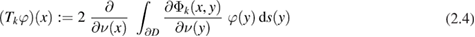
for 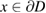 . For convenience of the reader we present the basic properties of acoustic single- and double-layer potentials in the contemporary Sobolev space setting. The single-layer potential
. For convenience of the reader we present the basic properties of acoustic single- and double-layer potentials in the contemporary Sobolev space setting. The single-layer potential
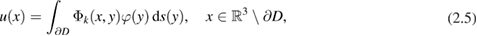
with density 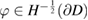 defines a bounded operator from
defines a bounded operator from  into both
into both 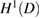 and
and  with boundary traces given by the jump relations
with boundary traces given by the jump relations

Here, by subscripts  and − we distinguish the traces taken in
and − we distinguish the traces taken in 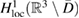 and
and  , respectively. The double-layer potential
, respectively. The double-layer potential

with density  defines a bounded operator from
defines a bounded operator from 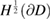 into both
into both 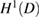 and
and  with boundary traces given by the jump relations
with boundary traces given by the jump relations
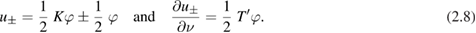
In analogy to Laplace's equation, the classical solution approach to the exterior Dirichlet problem (1.5) via boundary integral equations is to seek the solution  in the form of a double-layer potential (2.7) in
in the form of a double-layer potential (2.7) in  . The Dirichlet condition (1.5) is satisfied provided the density
. The Dirichlet condition (1.5) is satisfied provided the density  solves the integral equation of the second kind
solves the integral equation of the second kind 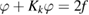 . It can be shown that this equation is uniquely solvable both in
. It can be shown that this equation is uniquely solvable both in  , assuming
, assuming  and in
and in  provided
provided  is not a Neumann eigenvalue for the negative Laplacian in the interior domain
is not a Neumann eigenvalue for the negative Laplacian in the interior domain  . This failure of the double-layer approach at the interior eigenvalues can be remedied by replacing (2.7) through a combined double- and single-layer potential of the form
. This failure of the double-layer approach at the interior eigenvalues can be remedied by replacing (2.7) through a combined double- and single-layer potential of the form
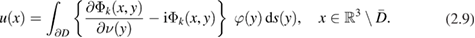
For the details of the analysis we refer the reader to [8, section 3.2].
Analogously, the approach to the exterior Neumann problem (1.6) via a single-layer approach fails when  is a Dirichlet eigenvalue for the negative Laplacian in
is a Dirichlet eigenvalue for the negative Laplacian in  . However, here the attempt to remedy this via the combined potential approach faces analytical and numerical challenges since the resulting integral equation
. However, here the attempt to remedy this via the combined potential approach faces analytical and numerical challenges since the resulting integral equation
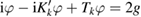
contains the hypersingular operator 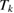 for the normal derivative of the double-layer potential. To obtain an integral equation that can be handled by using only the Riesz theory for compact operators, in 1965 Panich [24] suggested to include a smoothing operator in (2.9) and replace it by
for the normal derivative of the double-layer potential. To obtain an integral equation that can be handled by using only the Riesz theory for compact operators, in 1965 Panich [24] suggested to include a smoothing operator in (2.9) and replace it by
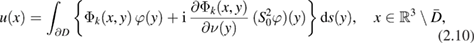
where  denotes the single-layer operator (2.1) in the potential theoretic limit case
denotes the single-layer operator (2.1) in the potential theoretic limit case  . For the resulting integral equation
. For the resulting integral equation

the Riesz theory is applicable both in 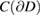 and
and  since
since 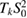 is compact. We note that in the 1960s when Panich made the above suggestion the boundary integral equations where discussed only in the classical function spaces of continuous and Hölder continuous functions and not yet in the contemporary Sobolev trace spaces. Injectivity for the operator on the left hand side of (2.11) follows from the fact that, for a solution
is compact. We note that in the 1960s when Panich made the above suggestion the boundary integral equations where discussed only in the classical function spaces of continuous and Hölder continuous functions and not yet in the contemporary Sobolev trace spaces. Injectivity for the operator on the left hand side of (2.11) follows from the fact that, for a solution  of the homogeneous form of the equation (2.11), with the aid of the potential theoretic jump relations the function
of the homogeneous form of the equation (2.11), with the aid of the potential theoretic jump relations the function  defined by (2.10) in the interior domain
defined by (2.10) in the interior domain 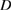 can be seen to satisfy the nonlocal impedance condition
can be seen to satisfy the nonlocal impedance condition

By Green's integral theorem and the self-adjointness of  , from (2.12) we have that
, from (2.12) we have that
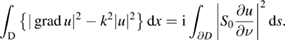
The positive definiteness of  now implies that
now implies that 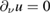 on
on 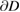 whence
whence 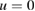 in
in  follows and consequently
follows and consequently 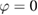 by the jump relations. For details again we refer to [8, section 3.2].
by the jump relations. For details again we refer to [8, section 3.2].
We conclude this section by noting that in (2.12) we may replace  by any positive definite pseudo differential operator of order
by any positive definite pseudo differential operator of order  . For example, using diagonal operators in terms of an orthogonal system (such as spherical harmonics) can create computational advantages as compared with the full matrix operator obtained by discretizing
. For example, using diagonal operators in terms of an orthogonal system (such as spherical harmonics) can create computational advantages as compared with the full matrix operator obtained by discretizing 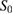 .
.
3. Scattering by a penetrable obstacle
Modeling scattering by a penetrable obstacle  with constant density
with constant density  and speed of sound
and speed of sound  differing from the density
differing from the density  and speed of sound
and speed of sound  in the surrounding background medium
in the surrounding background medium 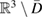 leads to a transmission problem. Here, in addition to the superposition
leads to a transmission problem. Here, in addition to the superposition 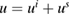 of the incoming wave
of the incoming wave 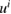 and the scattered wave
and the scattered wave 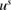 in
in  satisfying the Helmholtz equation with wave number
satisfying the Helmholtz equation with wave number  , we also have a transmitted wave
, we also have a transmitted wave  in
in  satisfying the Helmholtz equation with wave number
satisfying the Helmholtz equation with wave number  . The continuity of the pressure and of the normal velocity across the interface
. The continuity of the pressure and of the normal velocity across the interface 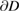 leads to the transmission conditions
leads to the transmission conditions

For the sake of simplicity, we only consider the case where 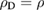 . The extension of the following analysis to the case
. The extension of the following analysis to the case 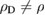 is straightforward. We also want to allow absorption, i.e. complex wave numbers
is straightforward. We also want to allow absorption, i.e. complex wave numbers 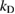 with non-negative real and imaginary part. For an incident field
with non-negative real and imaginary part. For an incident field 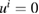 , by Green's integral theorem we find that
, by Green's integral theorem we find that
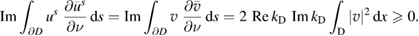
By theorem 2.13 in [8], as consequence of Rellich's lemma, it follows that 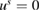 in
in  , that is, we have uniqueness for the solution.
, that is, we have uniqueness for the solution.
Usually this transmission problem is reduced to a two-by-two system of boundary integral equations over the interface  for a pair of unknowns, see among others [7, 16]. This can be done either by the direct method combining the Calderón projectors for the domains
for a pair of unknowns, see among others [7, 16]. This can be done either by the direct method combining the Calderón projectors for the domains 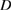 and
and 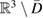 or by a potential approach in the indirect method. For a survey on methods for solving the transmission problem using only a single integral equation over
or by a potential approach in the indirect method. For a survey on methods for solving the transmission problem using only a single integral equation over 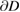 we refer to [15]. As an addition to the selection of available single integral equations for the transmission problem, in the present paper we will reduce the transmission problem to a scattering problem in
we refer to [15]. As an addition to the selection of available single integral equations for the transmission problem, in the present paper we will reduce the transmission problem to a scattering problem in 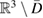 with a nonlocal impedance boundary condition in terms of the Dirichlet-to-Neumann operator for the domain
with a nonlocal impedance boundary condition in terms of the Dirichlet-to-Neumann operator for the domain 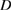 which then can be solved via one integral equation.
which then can be solved via one integral equation.
We assume that 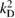 is not a Dirichlet eigenvalue for
is not a Dirichlet eigenvalue for 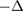 in the domain
in the domain  . Then the Dirichlet-to-Neumann operator
. Then the Dirichlet-to-Neumann operator
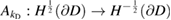
is well defined by the mapping taking 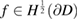 into the normal derivative
into the normal derivative 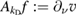 of the unique solution
of the unique solution 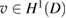 of
of 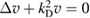 satisfying the Dirichlet condition
satisfying the Dirichlet condition 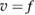 on
on 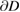 . From the single-layer approach for the interior Dirichlet problem we note the representation
. From the single-layer approach for the interior Dirichlet problem we note the representation

Then, for  , the transmission problem (3.1) can be seen to be equivalent to the scattering problem for
, the transmission problem (3.1) can be seen to be equivalent to the scattering problem for  in
in 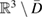 with the nonlocal impedance condition
with the nonlocal impedance condition

Once we have determined the scattered wave 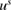 in
in 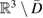 from (3.3), the transmitted wave
from (3.3), the transmitted wave  in
in  can be obtained via Green's representation theorem from its Cauchy data
can be obtained via Green's representation theorem from its Cauchy data 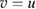 and
and  on
on 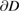 .
.
The single-layer potential

satisfies the boundary condition (3.3) provided the density 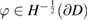 solves the equation
solves the equation

From the uniqueness for the solution of the transmission problem and consequently also for the solution of its equivalent reformulation (3.3) one can deduce that for a solution 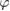 of the homogeneous form of (3.5) the corresponding potential (3.4) vanishes
of the homogeneous form of (3.5) the corresponding potential (3.4) vanishes 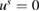 in
in 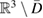 . Taking the boundary trace it follows that
. Taking the boundary trace it follows that  . If we assume that in addition to
. If we assume that in addition to 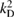 also
also 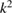 is not a Dirichlet eigenvalue for
is not a Dirichlet eigenvalue for 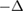 in
in 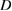 we have injectivity of
we have injectivity of  and therefore
and therefore  . Therefore the operator
. Therefore the operator 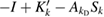 is injective.
is injective.
With the aid of (3.2) we rewrite
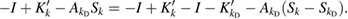
Since  is compact (see [8, lemma 5.37]) and the Dirichlet to Neumann operator is bounded from
is compact (see [8, lemma 5.37]) and the Dirichlet to Neumann operator is bounded from 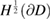 into
into  in addition to
in addition to  also
also 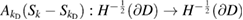 is compact. Thus, finally, the Riesz theory applies to equation (3.5) and we can summarize in the following theorem.
is compact. Thus, finally, the Riesz theory applies to equation (3.5) and we can summarize in the following theorem.
Theorem 3.1. Under the assumption that both  and
and  are not Dirichlet eigenvalues for the negative Laplacian in
are not Dirichlet eigenvalues for the negative Laplacian in 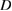 the equation (3.5) is uniquely solvable.
the equation (3.5) is uniquely solvable.
To avoid the restriction on 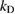 , instead of using the Dirichlet-to-Neumann operator, we propose to work with the Robin-to-Neumann operator
, instead of using the Dirichlet-to-Neumann operator, we propose to work with the Robin-to-Neumann operator
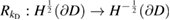
defined by the mapping taking 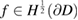 into the normal derivative
into the normal derivative  of the unique solution
of the unique solution 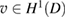 of
of 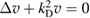 satisfying the Robin condition
satisfying the Robin condition

Uniqueness for the solution follows analogously to that for (2.12) by applying Green's integral theorem to  and
and  and taking the imaginary part. From the single-layer approach for the solution of (3.6) we observe that
and taking the imaginary part. From the single-layer approach for the solution of (3.6) we observe that

The corresponding nonlocal impedance condition now becomes
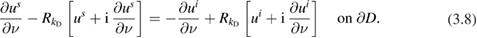
For all wave numbers 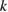 and
and 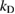 we are allowing, this impedance problem can be dealt with via a uniquely solvable integral equation as derived from the combined single- and double-layer approach (2.9). We omit working out the details.
we are allowing, this impedance problem can be dealt with via a uniquely solvable integral equation as derived from the combined single- and double-layer approach (2.9). We omit working out the details.
The Sommerfeld radiation condition is equivalent to the asymptotic behavior
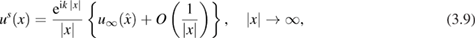
uniformly for all directions 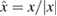 where the function
where the function 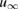 defined on the unit sphere
defined on the unit sphere 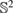 is known as the far field pattern of
is known as the far field pattern of  . One of the main inverse obstacle scattering problems is to determine the shape of the scatterer
. One of the main inverse obstacle scattering problems is to determine the shape of the scatterer 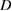 from the far field pattern
from the far field pattern  on
on  for one or several incident plane waves.
for one or several incident plane waves.
Some fifteen years ago in [17] a class of Newton type iterations for obstacle scattering problems was initiated which starts from a boundary integral equation approach for the solution of the forward scattering problem. Together with a corresponding representation of the far field pattern a system of two nonlinear integral equations for the unknown boundary  and a density function on the boundary as a sort of slip variable can be derived. For the above approach to the transmission problem this equation has the form
and a density function on the boundary as a sort of slip variable can be derived. For the above approach to the transmission problem this equation has the form

with the known far field pattern  and the operator
and the operator  given by
given by
describing the far field pattern of the single-layer potential (3.4). Then the basis of the inverse method under consideration can be cast into the following theorem.
Theorem 3.2. For a given incident field  and a given far field pattern
and a given far field pattern  , assume that the boundary
, assume that the boundary  and the density
and the density  satisfy the system (3.5) and (3.10). Then
satisfy the system (3.5) and (3.10). Then 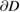 solves the inverse scattering problem.
solves the inverse scattering problem.
These two equations are nonlinear with respect to the boundary and ill-posed. Following [17] we suggest to solve them by simultaneous linearization with respect to both unknowns 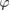 and
and 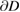 and iteration, i.e. by Newton iterations that require regularization because of the ill-posedness. We note that the derivatives of the operators in (3.5) and (3.10) can be written down explicitly in terms of boundary integral operators which offers computational advantages. For an overview and survey on this idea we refer to section 5.4 in [8] and to [10].
and iteration, i.e. by Newton iterations that require regularization because of the ill-posedness. We note that the derivatives of the operators in (3.5) and (3.10) can be written down explicitly in terms of boundary integral operators which offers computational advantages. For an overview and survey on this idea we refer to section 5.4 in [8] and to [10].
To conclude this section, we proceed with a couple of numerical examples in two dimensions as proof of concept. For a brief description we assume that the boundary curve  is given by a regular
is given by a regular 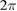 periodic parameterization
periodic parameterization
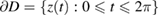
and we redefine the operators ![$ \newcommand{\demi}{\frac{1}{2}} S,K':H^{-\demi}[0,2\pi]\times C^2[0,2\pi]\to H^{\demi} [0,2\pi]$](https://content.cld.iop.org/journals/0266-5611/35/2/024002/revision2/ipaaf14eieqn170.gif) by
by
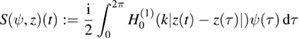
and
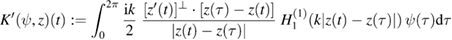
for ![$ t\in[0,2\pi]$](https://content.cld.iop.org/journals/0266-5611/35/2/024002/revision2/ipaaf14eieqn171.gif) as well as
as well as ![$ \newcommand{\demi}{\frac{1}{2}} \newcommand{\kreis}{\mathbb{S}^1} S_\infty:H^{-\demi}[0,2\pi]\times C^2[0,2\pi]\to L^2(\kreis)$](https://content.cld.iop.org/journals/0266-5611/35/2/024002/revision2/ipaaf14eieqn172.gif) given by
given by
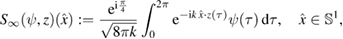
in their parameterized form. Here,  and
and 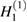 are the Hankel functions of order zero and one and of the first kind and we have indicated the dependence of the operators on
are the Hankel functions of order zero and one and of the first kind and we have indicated the dependence of the operators on 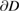 with parameterization
with parameterization  and we used the fundamental solution to the Helmholtz equation
and we used the fundamental solution to the Helmholtz equation  in
in 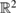 . For any vector
. For any vector  we denote
we denote 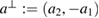 , that is,
, that is, 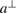 is obtained by rotating
is obtained by rotating  clockwise by 90 degrees.
clockwise by 90 degrees.
Now, setting 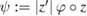 and multiplying the first equation by
and multiplying the first equation by 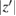 , the parameterized form of the system (3.5) and (3.10) becomes
, the parameterized form of the system (3.5) and (3.10) becomes
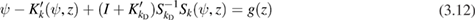
and

where
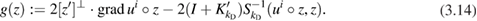
This system needs to be solved for 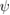 and
and  and we do this via linearization. Given an approximation for
and we do this via linearization. Given an approximation for 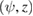 we solve the linearized equations
we solve the linearized equations
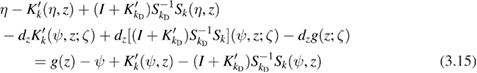
and
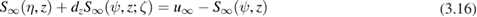
for  and update
and update  into
into 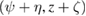 . These equations contain Fréchet derivatives of
. These equations contain Fréchet derivatives of  and
and 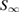 with respect to
with respect to  acting as linear operators on
acting as linear operators on 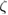 . These are obtained by differentiating the kernels with respect to
. These are obtained by differentiating the kernels with respect to  and for an explicit presentation we refer the reader, for example, to [19] where this inverse scattering method is applied to the inverse scattering problem with the local Leontovich impedance condition (1.7). Basic differentiation rules imply
and for an explicit presentation we refer the reader, for example, to [19] where this inverse scattering method is applied to the inverse scattering problem with the local Leontovich impedance condition (1.7). Basic differentiation rules imply
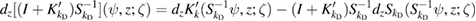
and, for plane wave incidence 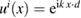 , we have
, we have
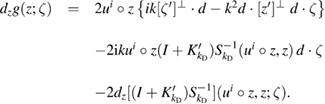
For finitely many incident fields  and corresponding far field patterns
and corresponding far field patterns  , one iteration step of our algorithmis is as follows: Given an approximation
, one iteration step of our algorithmis is as follows: Given an approximation  for the parameterization of the boundary
for the parameterization of the boundary  and
and  for the densities, after defining
for the densities, after defining  analogously to (3.14) in terms of
analogously to (3.14) in terms of  , we solve the linearized system
, we solve the linearized system
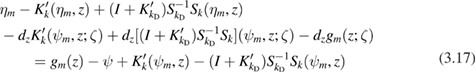
and
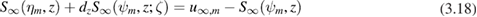
where 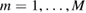 . We solve the system (3.17) and (3.18) of
. We solve the system (3.17) and (3.18) of 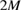 equations for the
equations for the 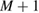 unknowns
unknowns  and
and  and update
and update  into
into  and
and  into
into  . For the initial step of the iteration only an initial guess for the shape
. For the initial step of the iteration only an initial guess for the shape  is required. The initial densities
is required. The initial densities 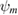 then can be obtained by solving (3.12).
then can be obtained by solving (3.12).
For the numerical implementation we need to discretize the boundary integral operators 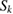 and
and 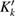 and their Fréchet derivatives. All four operators have weakly singular kernels with logarithmic singularities. For their numerical approximation by weighted trigonometric interpolation quadratures with spectral convergence we refer to [8].
and their Fréchet derivatives. All four operators have weakly singular kernels with logarithmic singularities. For their numerical approximation by weighted trigonometric interpolation quadratures with spectral convergence we refer to [8].
In our numerical examples we use parameterizations of the form
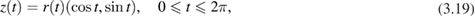
with a non-negative function  representing the radial distance of
representing the radial distance of  from the origin and approximate
from the origin and approximate  by trigonometric polynomials of degree
by trigonometric polynomials of degree  . We collocate the two equations (3.12) and (3.13), each at
. We collocate the two equations (3.12) and (3.13), each at 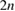 equidistant collocation points, the first equation at the points
equidistant collocation points, the first equation at the points  ,
, 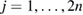 , and the second equation at the points
, and the second equation at the points 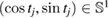 . The resulting linear system for the
. The resulting linear system for the 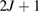 Fourier coefficients and the
Fourier coefficients and the 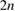 (or
(or  if we use
if we use 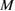 incident waves) nodal values of the density function
incident waves) nodal values of the density function  is solved in the least squares sense, penalized via Tikhonov regularization. As experienced in the application of regularized Newton iterations for related problems, it is advantageous to use an
is solved in the least squares sense, penalized via Tikhonov regularization. As experienced in the application of regularized Newton iterations for related problems, it is advantageous to use an  Sobolev penalty term for the shape rather than an
Sobolev penalty term for the shape rather than an 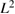 penalty in the Tikhonov regularization for some small
penalty in the Tikhonov regularization for some small  . For the density function just
. For the density function just 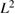 regularization suffices. Thus, in our Tikhonov functional we added the penalty term
regularization suffices. Thus, in our Tikhonov functional we added the penalty term 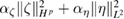 with regularization parameters
with regularization parameters  and
and 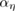 to the square of the
to the square of the  residual for the linear system (3.15) and (3.16).
residual for the linear system (3.15) and (3.16).
As pointed out already, the following two numerical examples are intended as proof of concept and not as presentation of an already fully developed method. In particular, the regularization parameters and the number of iterations were chosen by trial and error instead of, for example, a discrepancy principle. To avoid committing an inverse crime the synthetic far field data were obtained by solving the two-by-two system of integral equations presented in [16].
As boundary curves we considered a peanut-shaped obstacle with parametric representation
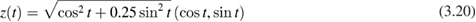
and an apple-shaped obstacle with parametric representation
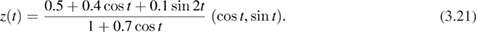
The wave numbers were 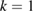 and
and  for both cases. The number of quadrature points was
for both cases. The number of quadrature points was 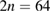 . The degree of the trigonometric polynomials was chosen as
. The degree of the trigonometric polynomials was chosen as  for exact data and
for exact data and  for perturbed data. The regularization parameter for an
for perturbed data. The regularization parameter for an  regularization for the shape was
regularization for the shape was 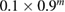 for the
for the 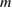 th iteration step for exact data and
th iteration step for exact data and  for perturbed data. The
for perturbed data. The 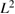 regularization parameter for the density was
regularization parameter for the density was  for exact data and
for exact data and 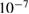 for perturbed data. The iteration was stopped after 20 iterations for exact data and 12 iterations for perturbed data, For the perturbed data, random noise was added point wise with relative error in the
for perturbed data. The iteration was stopped after 20 iterations for exact data and 12 iterations for perturbed data, For the perturbed data, random noise was added point wise with relative error in the 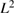 norm. The iterations were started with an initial guess given by a circle of radius
norm. The iterations were started with an initial guess given by a circle of radius 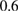 centered at the origin. For the peanut we used one incident wave with
centered at the origin. For the peanut we used one incident wave with 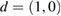 and for the apple two incident waves with
and for the apple two incident waves with 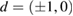 .
.
In figures 1 and 2 the exact  is given as dotted (magenta), the reconstruction as full (red) and the initial guess as dashed (blue) curve. They compare well with the reconstructions in [1] which were also obtained by the Kress–Rundell approach, but based on a two-by-two system for the transmission problem and with two incident waves for the peanut and four incident waves for the apple.
is given as dotted (magenta), the reconstruction as full (red) and the initial guess as dashed (blue) curve. They compare well with the reconstructions in [1] which were also obtained by the Kress–Rundell approach, but based on a two-by-two system for the transmission problem and with two incident waves for the peanut and four incident waves for the apple.
Figure 1. Reconstruction of the peanut (3.20) for exact data (left) and 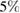 noise (right).
noise (right).
Download figure:
Standard image High-resolution imageFigure 2. Reconstruction of the apple (3.21) for exact data (left) and  noise (right).
noise (right).
Download figure:
Standard image High-resolution image4. A source problem
We proceed by considering scattering from an extended source described by an  function
function  with support in
with support in 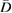 . Given a plane wave
. Given a plane wave  as incident field, the problem is to find the total field
as incident field, the problem is to find the total field  as a solution to the inhomogeneous Helmholtz equation
as a solution to the inhomogeneous Helmholtz equation

such that the scattered wave  satisfies the Sommerfeld radiation condition. Uniqueness of the solution follows from the observation that the difference of two solutions is an entire solution to the Helmholtz equation satisfying the radiation condition. Following similar ideas as in the previous section, we present a solution method by transforming this problem equivalently to a scattering problem in
satisfies the Sommerfeld radiation condition. Uniqueness of the solution follows from the observation that the difference of two solutions is an entire solution to the Helmholtz equation satisfying the radiation condition. Following similar ideas as in the previous section, we present a solution method by transforming this problem equivalently to a scattering problem in  with a nonlocal impedance condition on
with a nonlocal impedance condition on  .
.
The volume potential
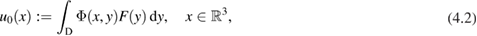
defines a solution of (4.1) and belongs to  (see [8]). Therefore the solution of the scattering problem also belongs to
(see [8]). Therefore the solution of the scattering problem also belongs to 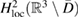 (see [8]) and consequently both the trace and the normal derivative trace on both sides of
(see [8]) and consequently both the trace and the normal derivative trace on both sides of  coincide.
coincide.
We assume that  is not a Dirichlet eigenvalue for
is not a Dirichlet eigenvalue for  in the domain
in the domain 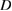 and make use of the Dirichlet-to-Neumann operator
and make use of the Dirichlet-to-Neumann operator  for
for  from the previous section, now with the wave number
from the previous section, now with the wave number 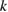 . For a solution
. For a solution  of (4.1) the function
of (4.1) the function 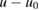 in
in 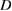 satisfies the Helmholtz equation and
satisfies the Helmholtz equation and
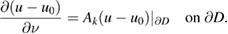
Therefore, in view of the continuity of the trace and the normal derivative across 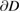 , the scattering problem from a source can equivalently be separated into two parts. First we solve the scattering problem for
, the scattering problem from a source can equivalently be separated into two parts. First we solve the scattering problem for  in
in  with the nonlocal impedance condition
with the nonlocal impedance condition

Then, knowing  on
on 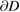 we solve for a solution to the Helmholtz equation
we solve for a solution to the Helmholtz equation  in
in 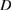 with Dirichlet values
with Dirichlet values  on
on  and set
and set  in
in 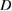 . Again we seek the scattered wave
. Again we seek the scattered wave 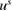 in the form of the single-layer potential (3.4) and the boundary condition
in the form of the single-layer potential (3.4) and the boundary condition
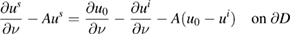
leads to an integral equation analogous to (3.5). As in the previous section the restriction on 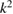 not a Dirichlet eigenvalue for
not a Dirichlet eigenvalue for  can be avoided by the use of a Robin-to-Neumann operator for
can be avoided by the use of a Robin-to-Neumann operator for  .
.
We note that instead of  given by the volume potential (4.2) one can use any special solution to (4.1). In particular, when
given by the volume potential (4.2) one can use any special solution to (4.1). In particular, when  is constant in
is constant in  a simple alternative is given by
a simple alternative is given by

In this particular case, the analogue of the two integral equations of the previous section can be employed for the solution of the inverse problem to determine  from the far field pattern
from the far field pattern 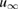 of the scattered wave. For the limiting case of a related problem for the Laplace case this method has been successfully implemented in two dimension by Kress and Rundell [18].
of the scattered wave. For the limiting case of a related problem for the Laplace case this method has been successfully implemented in two dimension by Kress and Rundell [18].
5. Transmission eigenvalues
Deviating for a couple of paragraphs from the theme of obstacle scattering, we consider the case of an inhomogeneous medium with space dependent refractive index  . We assume that
. We assume that  is real valued and nonnegative and that the contrast
is real valued and nonnegative and that the contrast  has support given by our obstacle domain
has support given by our obstacle domain 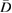 and is continuous in
and is continuous in 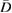 . Then, for an incident plane wave
. Then, for an incident plane wave 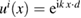 , the simplest inhomogeneous medium scattering problem is to find the total field
, the simplest inhomogeneous medium scattering problem is to find the total field  such that
such that 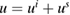 fulfills
fulfills

and 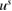 satisfies the Sommerfeld radiation condition (1.2).
satisfies the Sommerfeld radiation condition (1.2).
A complex number 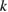 is called a transmission eigenvalue if there exist nontrivial functions
is called a transmission eigenvalue if there exist nontrivial functions 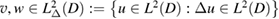 such that
such that 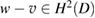 and
and

and

Here, the differential equations in (5.2) have to be understood in the distributional sense. In view of the the transmission condition (5.3) the space 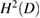 of functions
of functions  with vanishing trace
with vanishing trace  and normal trace
and normal trace  is the natural solution space for the difference
is the natural solution space for the difference  . Then from
. Then from

we observe that we must demand  . We endow
. We endow  with the norm
with the norm
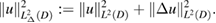
This transmission eigenvalue problem was introduced by Kirsch [11] in 1986 in connection with the completeness of the far field patterns 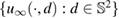 in
in  for scattering of plane waves from an inhomogeneous medium. In particular, this set of far field patterns is not complete if
for scattering of plane waves from an inhomogeneous medium. In particular, this set of far field patterns is not complete if 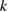 is a transmission eigenvalue.
is a transmission eigenvalue.
The transmission eigenvalues can be seen as an extension of the idea of resonant frequencies for impenetrable obstacles to the case of penetrable media and are related to non-scattering frequencies. If  is a real transmission eigenvalue and the corresponding eigenfunction
is a real transmission eigenvalue and the corresponding eigenfunction  can be extended outside
can be extended outside 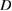 as an entire solution to the Helmholtz equation, then if the extended field is used as incident field the corresponding scattered wave is identically zero, i.e. this field does not scatter at the wave number
as an entire solution to the Helmholtz equation, then if the extended field is used as incident field the corresponding scattered wave is identically zero, i.e. this field does not scatter at the wave number  . Therefore it is not surprising that certain methods for the solution of the inverse scattering problem for inhomogeneous media such as the linear sampling method and the factorization method fail when
. Therefore it is not surprising that certain methods for the solution of the inverse scattering problem for inhomogeneous media such as the linear sampling method and the factorization method fail when  is a transmission eigenvalue. This inconvenient property explains why for a long time transmission eigenvalues were viewed as something to avoid and therefore left aside. It lasted 20 years after their introduction before Päivärinta and Sylvester [23] proved the existence of real transmission eigenvalues for the general case.
is a transmission eigenvalue. This inconvenient property explains why for a long time transmission eigenvalues were viewed as something to avoid and therefore left aside. It lasted 20 years after their introduction before Päivärinta and Sylvester [23] proved the existence of real transmission eigenvalues for the general case.
Together with his co-workers Armin Lechleiter [13, 21, 22], to whom this survey is dedicated, has given a promising characterization of the smallest real transmission eigenvalue 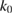 in terms of the behavior of the eigenvalues of the far field operator
in terms of the behavior of the eigenvalues of the far field operator 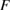 in the vicinity of their accumulation point zero when
in the vicinity of their accumulation point zero when  approaches
approaches 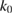 . The far field operator is just the integral operator with the far field pattern
. The far field operator is just the integral operator with the far field pattern  (for observation directions
(for observation directions 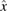 and incident directions
and incident directions  ) as kernel and is related to the scattering operator. This interesting relation between transmission eigenvalues and the eigenvalues of the far field operator is known as inside-outside duality for the far field operator and, together with monotonicity properties of transmission eigenvalues, might open up possibilities for designing a target signature for scatterers.
) as kernel and is related to the scattering operator. This interesting relation between transmission eigenvalues and the eigenvalues of the far field operator is known as inside-outside duality for the far field operator and, together with monotonicity properties of transmission eigenvalues, might open up possibilities for designing a target signature for scatterers.
Here, following work of Cossonnière and Haddar [9] and Cakoni and Kress [5], we want to illustrate how boundary integral equations can be used to characterize and numerically compute transmission eigenvalues in the case were  is constant in
is constant in  . We need to adjust the spaces in which we must investigate the boundary integral operators since we have to search for the eigenfunctions
. We need to adjust the spaces in which we must investigate the boundary integral operators since we have to search for the eigenfunctions  in
in 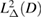 . This implies that their trace and their normal derivative on the boundary belong to
. This implies that their trace and their normal derivative on the boundary belong to 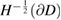 and
and 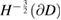 , respectively, and are defined by duality. Motivated by Green's integral theorem
, respectively, and are defined by duality. Motivated by Green's integral theorem
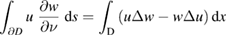
for  with
with 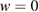 on
on 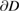 , for
, for 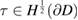 we define the duality pairing
we define the duality pairing
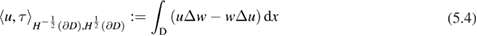
where  is biharmonic in
is biharmonic in  such that
such that  and
and  on
on 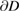 . However, we note that he right hand side of (5.4) has the same value for all
. However, we note that he right hand side of (5.4) has the same value for all 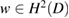 with boundary traces
with boundary traces  and
and 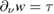 on
on  . The well-posedness of the biharmonic Dirichlet problem (see, among others [3]) implies
. The well-posedness of the biharmonic Dirichlet problem (see, among others [3]) implies
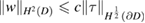
with some positive constant  independent of
independent of  . Consequently
. Consequently
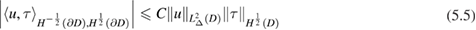
for all 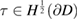 and some positive constant
and some positive constant 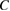 . Thus for each
. Thus for each 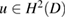 by (5.4) we have defined a bounded linear functional
by (5.4) we have defined a bounded linear functional  with
with

that means  is a bounded operator. By denseness we can extend
is a bounded operator. By denseness we can extend 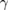 as a bounded operator
as a bounded operator 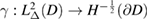 .
.
Analogously, for 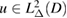 the normal trace
the normal trace 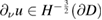 is defined by duality using the identity
is defined by duality using the identity
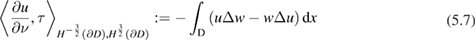
where  is such that
is such that  and
and  on
on 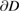 . Then we also have
. Then we also have

for some positive constant  .
.
For convenience we introduce the wave number for the refracting case by
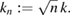
As in the direct boundary integral equation approach to the classical transmission problem of section 3, Cossonnière and Haddar combined the Calderón projectors for the wave numbers 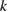 and
and  in the domain
in the domain  . From Green's representation theorem and the potential theoretic jump relations it follows that for a solution
. From Green's representation theorem and the potential theoretic jump relations it follows that for a solution  to
to  we have that
we have that

The validity of this Calderón equation for  can be justified from the classical spaces by denseness arguments. We now combine (5.9) with the corresponding equation for
can be justified from the classical spaces by denseness arguments. We now combine (5.9) with the corresponding equation for  to observe that if
to observe that if  is a transmission eigenvalue then the operator
is a transmission eigenvalue then the operator  defined by
defined by
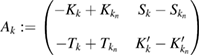
has a nontrivial kernel in  , that is, the transmission eigenvalue
, that is, the transmission eigenvalue 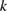 is an eigenvalue of
is an eigenvalue of 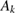 considered as a nonlinear and analytic operator in
considered as a nonlinear and analytic operator in  .
.
The main result of Cossonnière and Haddar [9] for this two-by-two system now can be stated as the following theorem.
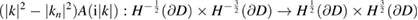
is coercive and the operator
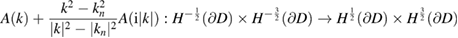
is compact.
The main tools for its proof are Green's integral theorem for the coercitivity and an elaborate analysis of the mapping properties of the difference of the boundary integral operators for  and
and  . In particular, this result implies that the analytic Fredholm theory can be used to deduce the discreteness of transmission eigenvalues, a result that had been established some 30 years ago by Colton et al [6] and Rynne and Sleeman [25] by different concepts.
. In particular, this result implies that the analytic Fredholm theory can be used to deduce the discreteness of transmission eigenvalues, a result that had been established some 30 years ago by Colton et al [6] and Rynne and Sleeman [25] by different concepts.
The above boundary integral equation formulation of Cossonnière and Haddar was used by Kleefeld [14] for actual computations of transmission eigenvalues with the aid of the attractive new algorithm for solving nonlinear eigenvalue problems for large sized matrices that are analytic with respect to the eigenvalue parameter as proposed by Beyn [2]. We note that exterior transmission eigenvalues in  are also eigenvalues of
are also eigenvalues of  which has to be taken into account in the numerical implementation in an appropriate way. Before Kleefeld's work, in the literature, the majority of numerical methods were based on finite element methods applied after a transformation of the transmission eigenvalue problem to a generalized eigenvalue problem for a fourth order partial differential equation.
which has to be taken into account in the numerical implementation in an appropriate way. Before Kleefeld's work, in the literature, the majority of numerical methods were based on finite element methods applied after a transformation of the transmission eigenvalue problem to a generalized eigenvalue problem for a fourth order partial differential equation.
As for the classical transmission problem as discussed in section 3, one can also try to base the transmission eigenvalue problem on only one integral equation via the Dirichlet-to-Neumann operator for the domain  . This idea was pursued by Cakoni and Kress [5]. Assuming that
. This idea was pursued by Cakoni and Kress [5]. Assuming that 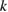 and
and 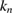 are not Dirichlet eigenvalues of
are not Dirichlet eigenvalues of  in the domain
in the domain  , we have that
, we have that  is a transmission eigenvalue if and only if the kernel of the operator
is a transmission eigenvalue if and only if the kernel of the operator 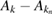 given by the difference of the Dirichlet-to-Neumann operators for the wave numbers
given by the difference of the Dirichlet-to-Neumann operators for the wave numbers 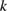 and
and 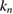 is nontrivial. To avoid the annoying restriction on the wave numbers instead of using the Dirichlet-to-Neumann operator, Cakoni and Kress [5] originally worked with the Robin-to-Neumann operator defined by the Leontovich impedance condition (1.7). However, later it was discovered that the related analysis can be simplified by replacing (1.7) by a nonlocal impedance condition analogous to (2.12). For this, taking into account that we require
is nontrivial. To avoid the annoying restriction on the wave numbers instead of using the Dirichlet-to-Neumann operator, Cakoni and Kress [5] originally worked with the Robin-to-Neumann operator defined by the Leontovich impedance condition (1.7). However, later it was discovered that the related analysis can be simplified by replacing (1.7) by a nonlocal impedance condition analogous to (2.12). For this, taking into account that we require  solutions in the analysis of the transmission eigenvalues, we redefine the Robin-to-Neumann operator by
solutions in the analysis of the transmission eigenvalues, we redefine the Robin-to-Neumann operator by
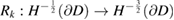
as the mapping taking 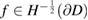 into the normal derivative
into the normal derivative 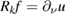 of the unique solution
of the unique solution  of
of  satisfying the nonlocal impedance boundary condition
satisfying the nonlocal impedance boundary condition

Here  is a positive definite pseudo-differential operator of order
is a positive definite pseudo-differential operator of order 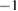 .
.
The first task is to establish the well-posedness of this boundary value problem in the required space 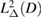 . One of our main tools in the subsequent analysis is the following regularity result for the Poisson equation. To avoid tedious adjustments of the regularity assumptions on
. One of our main tools in the subsequent analysis is the following regularity result for the Poisson equation. To avoid tedious adjustments of the regularity assumptions on 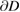 related to the order of the respective Sobolev trace spaces for each of the following statements, for the remainder of our paper we assume that
related to the order of the respective Sobolev trace spaces for each of the following statements, for the remainder of our paper we assume that  is
is  smooth.
smooth.
Lemma 5.2. Let 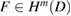 and
and  . Then the unique solution
. Then the unique solution 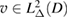 of
of 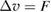 in
in 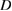 and
and 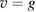 on
on 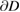 belongs to
belongs to  and the mapping taking
and the mapping taking  into
into  is bounded from
is bounded from  into
into 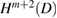 for
for 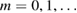
Proof. By theorem 1.3 in [26, p 305] the unique solution 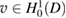 of
of 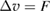 for
for  belongs to
belongs to 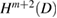 and the mapping taking
and the mapping taking 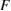 into
into  is bounded from
is bounded from 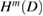 into
into 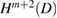 for
for 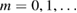 .
.
First we show that this result can be extended to solutions  that vanish on
that vanish on 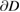 in the sense of the
in the sense of the 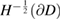 trace. For this we observe from the definition (5.4) that for any harmonic function
trace. For this we observe from the definition (5.4) that for any harmonic function  with vanishing trace on the boundary
with vanishing trace on the boundary 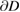 we have that
we have that  for all
for all  with
with 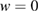 on
on  . Inserting the solution
. Inserting the solution  of
of  which by the above automatically belongs to
which by the above automatically belongs to  yields
yields  in
in  . For a solution
. For a solution 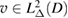 of
of  for
for  with vanishing
with vanishing 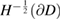 trace on
trace on 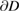 we denote by
we denote by 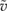 the solution of
the solution of 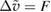 in
in 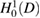 and apply the just established uniqueness result for the difference
and apply the just established uniqueness result for the difference  to obtain that
to obtain that  .
.
The statement of the lemma now follows from the observation that the unique solution 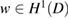 of the Laplace equation
of the Laplace equation  satisfying
satisfying  on
on  for
for  is in
is in  and that the mapping taking
and that the mapping taking 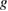 into
into  is bounded from
is bounded from 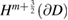 into
into  as can be observed from the single-layer boundary integral equation approach and the mapping properties of the the single-layer potential. □
as can be observed from the single-layer boundary integral equation approach and the mapping properties of the the single-layer potential. □
Now we establish uniqueness for a solution 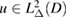 to (5.10). From
to (5.10). From  and the assumptions on
and the assumptions on 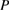 we observe that
we observe that  has boundary trace in
has boundary trace in  . Hence by lemma 5.2 we have
. Hence by lemma 5.2 we have  and uniqueness for all
and uniqueness for all 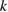 with positive real and nonnegative imaginary part now follows analogously to that for (2.12).
with positive real and nonnegative imaginary part now follows analogously to that for (2.12).
In order to represent the Robin-to-Neumann operator we introduce the single-layer potential 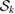 defined by
defined by
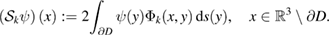
In particular, it is known that the operator  , its restriction
, its restriction  and the normal derivative operator
and the normal derivative operator 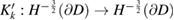 all are bounded (see [12, 20]). Further, the jump relations for the single-layer potential can be extended to the case of
all are bounded (see [12, 20]). Further, the jump relations for the single-layer potential can be extended to the case of  densities and, if
densities and, if  is not a Dirichlet eigenvalue of
is not a Dirichlet eigenvalue of 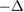 for
for  then
then  is an isomorphism.
is an isomorphism.
The single-layer potential with density  satisfies (5.10) provided
satisfies (5.10) provided  satisfies the equation
satisfies the equation

where

From uniqueness both for the interior problem (5.10) in  and for the exterior Dirichlet problem together with the jump relations for the single-layer potential it can be deduced that
and for the exterior Dirichlet problem together with the jump relations for the single-layer potential it can be deduced that  has a trivial kernel in
has a trivial kernel in 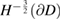 for all
for all  with positive real part and nonnegative imaginary part. After picking a wave number
with positive real part and nonnegative imaginary part. After picking a wave number 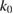 such that
such that  is not a Dirichlet eigenvalue for
is not a Dirichlet eigenvalue for  in
in  we write
we write 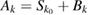 where
where 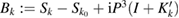 . Then
. Then 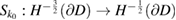 is an isomorphism and
is an isomorphism and  is compact since the difference
is compact since the difference 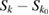 is bounded from
is bounded from  into
into 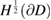 (see [8, lemma 5.37]) and
(see [8, lemma 5.37]) and 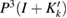 is bounded from
is bounded from 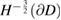 into
into  because of our assumption on
because of our assumption on  . Therefore, by the Riesz theory
. Therefore, by the Riesz theory 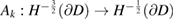 is an isomorphism and we can write
is an isomorphism and we can write

Hence, we finally can state that 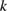 is a transmission eigenvalue if and only if the operator
is a transmission eigenvalue if and only if the operator

has a nontrivial kernel in  .
.
We note that if for positive  we define
we define

then analogous to the above it can shown that  is an isomorphism and
is an isomorphism and 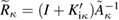 represents the Robin-to-Neumann operator for
represents the Robin-to-Neumann operator for 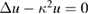 in
in  with boundary condition
with boundary condition

for a given  . Setting
. Setting  , we also have that
, we also have that 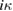 is a transmission eigenvalue if and only if the operator
is a transmission eigenvalue if and only if the operator

has a nontrivial kernel in 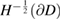 .
.
We now want to show that
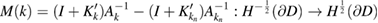
is a Fredholm operator of index zero. Our analysis is based on the properties of the difference of the single-layer potentials

for  for which we expect
for which we expect 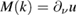 . We collect these properties in the following lemma.
. We collect these properties in the following lemma.
Lemma 5.3. For  define
define  by (5.18). Then
by (5.18). Then 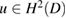 and
and  with the mappings
with the mappings 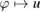 bounded from
bounded from  into
into 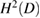 and
and  bounded from
bounded from 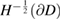 into
into  such that
such that

for some positive constant  independent of
independent of 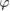 . Further we have the differential equation
. Further we have the differential equation

and the boundary conditions
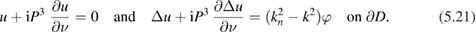

we observe that  is in
is in  with the mapping
with the mapping 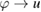 bounded from
bounded from 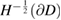 into
into 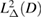 . The differential equation (5.20) is obvious and via
. The differential equation (5.20) is obvious and via  it implies that
it implies that  in
in  with the estimate (5.19) and that the mapping
with the estimate (5.19) and that the mapping  is bounded from
is bounded from 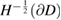 into
into  . Furthermore we have
. Furthermore we have
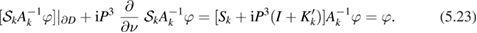
Subtracting from this the corresponding equation for the wave number 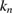 the first of the boundary conditions (5.21) follows. Multiplying (5.23) by
the first of the boundary conditions (5.21) follows. Multiplying (5.23) by  and subtracting the corresponding equation for the wave number
and subtracting the corresponding equation for the wave number  in view of (5.22) we obtain the second of the boundary conditions (5.21).
in view of (5.22) we obtain the second of the boundary conditions (5.21).
Since 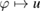 is bounded from
is bounded from 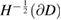 into
into  we have that
we have that 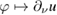 is bounded from
is bounded from 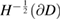 to
to 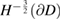 and our assumption on the operator
and our assumption on the operator 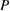 ensures that the mapping
ensures that the mapping  is bounded from
is bounded from 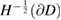 into
into 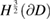 . Now, the first boundary condition in (5.21) and lemma 5.2 for
. Now, the first boundary condition in (5.21) and lemma 5.2 for  imply that
imply that 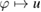 is bounded from
is bounded from 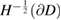 into
into 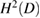 . □
. □
Analogously, for 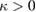 the statement of this lemma carries over to
the statement of this lemma carries over to

with (5.20) and (5.21) replaced by

and
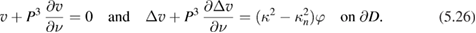
Corollary 5.4. The linear operators  are bounded.
are bounded.
Proof. The statement is obtained by taking the normal traces of the mappings 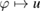 and
and  . □
. □
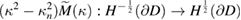
is coercive.
Proof. For  with
with 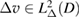 , using Green's integral theorem, we can transform
, using Green's integral theorem, we can transform
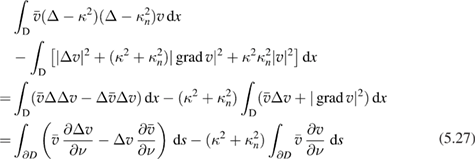
where the integrals over  containing
containing  and
and  are to be understood in the sense of the dualities (5.4) and (5.7). In this expression the second domain integral is equivalent to the
are to be understood in the sense of the dualities (5.4) and (5.7). In this expression the second domain integral is equivalent to the  norm as can be seen with the aid of Green's representation formula, that is,
norm as can be seen with the aid of Green's representation formula, that is,
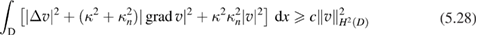
for all  and some constant
and some constant 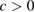 .
.
Now, for  we consider
we consider  as defined by (5.24). From the boundary conditions (5.26) and the self adjointness of
as defined by (5.24). From the boundary conditions (5.26) and the self adjointness of 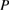 we observe that
we observe that
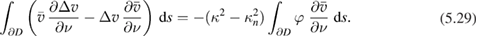
Then (5.25), (5.27) and (5.29) imply
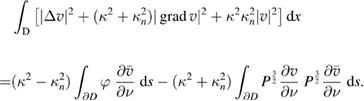
Inserting 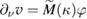 and using the positive definiteness of
and using the positive definiteness of  and the estimate (5.28) we obtain
and the estimate (5.28) we obtain
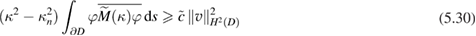
for some constant 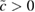 . From the boundary condition (5.26), the boundedness of
. From the boundary condition (5.26), the boundedness of 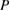 , the trace estimates (5.6) and (5.8), applied to
, the trace estimates (5.6) and (5.8), applied to  , and the estimate (5.19) we can conclude that
, and the estimate (5.19) we can conclude that
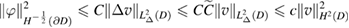
for some positive constant  . Inserting this estimate into (5.30) finishes the proof. □
. Inserting this estimate into (5.30) finishes the proof. □
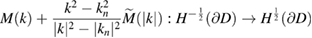
is compact.
Proof. For  we consider
we consider  defined by (5.18) and
defined by (5.18) and  defined by (5.24) for
defined by (5.24) for  and let
and let

From (5.21) and (5.26) we can deduce the boundary conditions

and

on  . (We note that the coefficient in the definition of
. (We note that the coefficient in the definition of  in (5.31) is chosen such that we obtain (5.33).) Since the mappings
in (5.31) is chosen such that we obtain (5.33).) Since the mappings  and
and  are bounded from
are bounded from 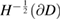 into
into  , in view of our assumption on
, in view of our assumption on  , the right hand side
, the right hand side 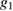 of (5.32) is in
of (5.32) is in 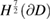 with the mapping
with the mapping  bounded from
bounded from  into
into  . Because the mappings
. Because the mappings 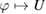 and
and 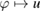 also are bounded from
also are bounded from 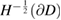 into
into 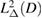 The right hand side
The right hand side  of (5.33) is in
of (5.33) is in 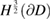 with the mapping
with the mapping 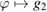 bounded from
bounded from  into
into  .
.
Furthermore, it is straightforward to check that
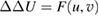
where
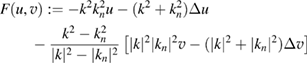
belongs to 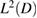 with the mapping
with the mapping 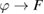 bounded from
bounded from 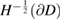 to
to 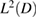 .
.
Now, we can use lemma 5.2 again. Applying it first for 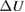 we obtain that
we obtain that  with the mapping
with the mapping 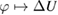 bounded from
bounded from  into
into  . Applying the lemma then for
. Applying the lemma then for  shows that
shows that  with the mapping
with the mapping  bounded from
bounded from  into
into 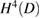 . Therefore, the mapping
. Therefore, the mapping 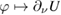 is bounded from
is bounded from  into
into  . Now, in view of
. Now, in view of
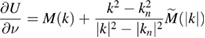
the statement of the theorem follows from the compact embedding of 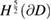 into
into  . □
. □
Noting that 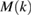 is analytic in
is analytic in 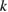 since the kernels of
since the kernels of 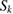 and
and  are analytic in
are analytic in 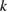 , now theorems 5.5 and 5.6 imply the following final result. From this, in particular, we can again reestablish the discreteness of the set of transmission eigenvalues for the special case of a constant refractive index and the finite multiplicity of the transmission eigenvalues.
, now theorems 5.5 and 5.6 imply the following final result. From this, in particular, we can again reestablish the discreteness of the set of transmission eigenvalues for the special case of a constant refractive index and the finite multiplicity of the transmission eigenvalues.
Theorem 5.7. 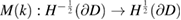 is a Fredholm operator with index zero and analytic in
is a Fredholm operator with index zero and analytic in  .
.
Cakoni and Kress [5] also used their boundary integral equation formulation for actual computations of transmission eigenvalues with the aid of Beyn's [2] algorithm mentioned above. Comparing the computational costs for Beyn's algorithm as applied to Cossonnière and Haddar's two-by-two system it can be shown that the approach presented here reduces the costs by about 50 percent. For details of the implementation and numerical results we refer to [5] and for a very recent extension of this approach to the Maxwell equations including numerical results for transmission eigenvalues in three dimensions we refer the reader to [4].




