Electron and phonon transport properties of layered Bi₂O₂Se and Bi₂O₂Te from first-principles calculations

Both Bi₂O₂Se and Bi₂O₂Te belong to the tetragonal structure with I4/mmm space group (figure 1(a)). Our optimized equilibrium lattice constants shown in table 1 are consistent with the experimental values [17, 21] and other theoretical values [33]. Based on the equilibrium structures, we firstly calculate the band structure of Bi₂O₂X, as shown in figures 1(b) and (c). It is clear that both Bi₂O₂Se and Bi₂O₂Te are semiconductors with indirect energy gaps of 0.87 eV and 0.21 eV, respectively, which are in agreement with the previous experimental and theoretical values [21, 33] (see table 1). Furthermore, we calculate the total and atomic partial density of states (DOS) near the Fermi level. It can be extracted from figure 2 that the conduction bands around the Fermi level are mostly contributed by Bi 6p states, and the valence bands originate from the hybridized states of Se (Te) p states and O 2p states. At the same time, the valence bands exhibit much higher DOS than the conduction bands, and thus one can expect that the Seebeck coefficient of p-type is much larger than that of n-type by reasonable doping.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Next, we calculate the electronic transport properties by the semiclassical Boltzman transport theory. With so-called constant relaxation time approximation, the Seebeck coefficient S is independent of the relaxation time τ, while the electrical conductivity σ is dependent on τ. In the present work, by fitting the calculated Seebeck coefficient and electrical conductivity with the experimental results for Bi₂O₂X at 300 and 500 K [17, 21], we obtain the carrier concentration n and the relaxation time τ. For Bi₂O₂Se, n is 2.85 × 10^–18 cm⁻³ at 300 K and 2.34 × 10^–18 cm⁻³ at 500 K, and τ is 1.35 × 10^–15 s at 300 K and 1.91 × 10^–15 s at 500 K. For Bi₂O₂Te, n is 1.06 × 10^–18 cm⁻³ at 300 K and 6.15 × 10^–18 cm⁻³ at 500 K, and τ is 2.51 × 10^–15 s at 300 K and 3.43 × 10^–15 s at 500 K. The obtained carrier concentrations are in agreement with the experimental values ∼10^–18 cm⁻³ [21, 34], and their changes with temperature are slight [34]. The fitted τ values at 300 K are close to the previous theoretical results of 1.2 × 10^–15 s for Bi₂O₂Se [35] and 4.4 × 10^–15 s for Bi₂O₂Te [22]. Figures 3(a) and (b) show the calculated S and σ as a function of carrier concentration at 300 K. It is noticed that the Seebeck coefficient of p-type doping is larger than the n-type doping, and this characteristic is consistent with the DOS that the valence bands exhibit much higher DOS than the conduction bands. Both p-type Seebeck coefficients of Bi₂O₂Se and Bi₂O₂Te can reach about 450 μV K⁻¹ at an appropriate carrier concentration. We note that the previous theoretical S of −93 μV K⁻¹ at the n-type carrier concentration of 1.5 × 10¹⁹ cm⁻³ and 400 μV K⁻¹ at the p-type carrier concentration of 2.0 × 10¹⁹ cm⁻³ [35] are close to our present results of −85 μV K⁻¹ and 370 μV K⁻¹, respectively (see figure 3(a)).

Zoom In Zoom Out Reset image size

Figure 3(b) indicates that, compared with Bi₂O₂Se, the electrical conductivity of Bi₂O₂Te is higher due to the small band gap. The electrical conductivity rapidly increases as the increasing carrier concentration, while the change is reverse for the Seebeck coefficient, and thus it is natural to obtain the maximum power factor by fitting a balanced value of the carrier concentration between the Seebeck coefficient and the electrical conductivity. Indeed, It can be clearly seen from figure 4 that Bi₂O₂Se shows the best power factor of 1.39 mW mK⁻² at a concentration of 1.05 × 10²¹ cm⁻³ for p-type doping at 500 K, while the maximum power factor of Bi₂O₂Te is about 1.13 mW mK⁻² with the concentration of 3.08 × 10²⁰ cm⁻³ for p-type doping at 500 K. As for Bi₂O₂Te, the power factor of n-type doping increases with the increase of temperature, which is consistent with the experimental results [21]. The calculated electrical thermal conductivity κ_e is shown in figure 3(c). One can see that the p-type value is clearly lower than the n-type value at the same carrier concentration. Overall, all these results indicate that the thermoelectric performance of the p-type doping is more favorable than the n-type doping. The electronic transport performance can be enhanced by reasonable p-type doping.

Zoom In Zoom Out Reset image size

The calculated phonon spectra of Bi₂O₂X are plotted along high-symmetry paths in figure 5(a). As the primitive cells of Bi₂O₂X (X = Se, Te) have five atoms, fifteen phonon branches can be observed. There are significant frequency gaps between the high-frequency and low-frequency modes of optical branches, and they are about 3.03 THz and 3.12 THz for Bi₂O₂Se and Bi₂O₂Te, respectively. Meanwhile, we find some special features from the phonon spectra. One point of interest is the fact that compared with acoustic branches and low-frequency optical branches, the high-frequency optical branches show distinct dispersion, indicating their higher group velocity. What's more, acoustic branches and some optical branches show different dispersions along the cross-plane (Γ–Z) and in-plane (Γ–X) directions, which suggests a strong phonon anisotropy as discussed in detail below. It can also be seen that all the phonon branches moves toward lower frequency for Bi₂O₂Te compared to Bi₂O₂Se, which implies the phonon spectra become more localized, namely the coupling strength between low-frequency optical branches and acoustic branches is enhanced. We also present in figure 5(b) the calculated total and partial phonon DOS. The optical modes with high frequency of Bi₂O₂X are dominated by O atoms, while the acoustic branches and low-frequency optical branches are mainly governed by Bi and Se (Te) atoms. Such distributions are mainly responsible for the large mass difference between O and Bi (Se, Te) atoms, because the frequencies of lighter (heavier) atoms are higher (lower).

Zoom In Zoom Out Reset image size

The calculated phonon group velocity with respect to frequency is shown in figure 6. It can be seen that the optical phonon branches also show remarkable dispersion, which points to higher group velocities of these optical modes, and their contributions to lattice thermal conductivity cannot be ignored. In addition, as for Bi₂O₂Se, the group velocities of transverse acoustic (TA) branches and longitudinal acoustic (LA) branch along Γ–X are about 1.54 km s⁻¹, 1.34 km s⁻¹ and 4.02 km s⁻¹, respectively, while the group velocities of TA and LA along Γ–Z are about 1.22 km s⁻¹, 2.32 km s⁻¹ and 4.2 km s⁻¹. As for high-frequency optical branches, the maximum group velocity along Γ–X reaches 7.51 km s⁻¹, whereas it is only 0.57 km s⁻¹ along Γ–Z. Likewise, the group velocities along Γ–X and Γ–Z for Bi₂O₂Te also show large difference. Thus, the group velocities along in-plane are much different from those along cross-plane direction, which will lead to a strong anisotropy of lattice thermal conductivity. In addition, compared with Bi₂O₂Se, Bi₂O₂Te possessing of heavier atomic mass has smaller group velocities.

Zoom In Zoom Out Reset image size

The calculated lattice thermal conductivity of Bi₂O₂X as a function of temperature is shown in figure 7. Both Bi₂O₂Se and Bi₂O₂Te exhibit fairly low lattice thermal conductivities. The room temperature lattice thermal conductivities are 1.14 W m⁻¹ K⁻¹ for Bi₂O₂Se and 0.58 W m⁻¹ K⁻¹ for Bi₂O₂Te, which are lower than those of 1.6 W m⁻¹ K⁻¹ for PbTe [36] and 0.97 W m⁻¹ K⁻¹ for SnSe [37], respectively. They are also close to the experimental values of 1.1 W m⁻¹K⁻¹ for Bi₂O₂Se [17] and 0.91 W m⁻¹ K⁻¹ for Bi₂O₂Te [21]. When the temperature is raised to 800 K, the lattice thermal conductivities are merely 0.45 W m⁻¹ K⁻¹ and 0.22 W m⁻¹ K⁻¹ for Bi₂O₂Se and Bi₂O₂Te, respectively. The lattice thermal conductivity of Bi₂O₂Te is lower than that of Bi₂O₂Se due to the lower group velocity induced by heavier Te atom in Bi₂O₂Te than Se atom in Bi₂O₂Se. Interestingly, both lattice thermal conductivities exhibit strong anisotropy. For example, the in-plane and cross-plane room temperature lattice thermal conductivities are 1.31 and 0.82 W m⁻¹ K⁻¹ for Bi₂O₂Se, and 0.83 and 0.09 Wm⁻¹K⁻¹ for Bi₂O₂Te. The origin of the anisotropic lattice thermal conductivity can be explained from two aspects. On the one hand, as mentioned above, the acoustic branches and some optical branches show different dispersions along the cross-plane (Γ–Z) and in-plane (Γ–X) directions, which results in different group velocities along the cross-plane and in-plane directions. On the other hand, the atomic interactions along the cross-plane (weak electrostatic interactions) and in-plane directions (strong covalent bonding interactions) are different [38]. The weak electrostatic interactions along the cross-plane direction limit the phonon transport and yield low κ_l.

Zoom In Zoom Out Reset image size

To further reveal the thermal transport mechanism, we show in figure 8 the calculated total relaxation time for all phonon modes as a function of frequency. Here, the phonon relaxation time τ_λ can be obtained from the phonon linewidth 2Γ_λ(ω_λ) of the phonon mode λ:

$$\begin{eqnarray}&&{\tau }_{\lambda }=\displaystyle \frac{1}{2{{\rm{\Gamma }}}_{\lambda }({\omega }_{\lambda })}.\end{eqnarray} \tag{ 1 }$$

The Γ_λ(ω) takes a form analogous to the Fermi golden rule:

$$\begin{eqnarray}&&\begin{array}{l}{{\rm{\Gamma }}}_{\lambda }(\omega )=\displaystyle \frac{18}{{\hslash }^{2}}\displaystyle \sum _{\lambda ^{\prime} \lambda ^{\prime\prime} }{| {{\rm{\Phi }}}_{-\lambda \lambda ^{\prime} \lambda ^{\prime\prime} }| }^{2}[({f}_{\lambda }^{{\prime} }+{f}_{\lambda }^{{\prime\prime} }+1)\delta (\omega -{\omega }_{\lambda }^{{\prime} }-{\omega }_{\lambda }^{{\prime\prime} })\\ \,+\,({f}_{\lambda }^{{\prime} }-{f}_{\lambda }^{{\prime\prime} })[\delta (\omega +{\omega }_{\lambda }^{{\prime} }-{\omega }_{\lambda }^{{\prime\prime} })-\delta (\omega -{\omega }_{\lambda }^{{\prime} }+{\omega }_{\lambda }^{{\prime\prime} })]],\end{array}\end{eqnarray} \tag{ 2 }$$

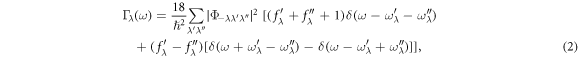
where f_λ is the phonon equilibrium occupancy, and ${{\rm{\Phi }}}_{-\lambda \lambda ^{\prime} \lambda ^{\prime\prime} }$ is the strength of interaction among the three phonons, λ, λ', and λ'', involved in the scattering. Please see [39] about the more detailed description of these calculations. From figure 8, one can see that the average relaxation times are 1.3 ps for Bi₂O₂Se and 2.1 ps for Bi₂O₂Te for the acoustic branches and low-frequency optical branches (below 6 THz), and 0.41 ps for Bi₂O₂Se and 0.23 ps for Bi₂O₂Te for the high-frequency optical branches (above 6 THz), these values have the same magnitude to that of PbTe [40] which has a very dispersive transverse optical branch. Therefore, like PbTe, such low relaxation times in Bi₂O₂X are mainly attributed to the large phonon scattering. Importantly, the low-frequency optical phonon modes, as coupled with acoustic modes, possess comparable relaxation times with acoustic phonon modes, in contrast the high-frequency optical modes exhibit lower relaxation times. This means that the low-frequency optical phonons also make a dominate contribution to the lattice thermal conductivity.

Zoom In Zoom Out Reset image size

We have also calculated the cumulative thermal conductivity as a function of phonon maximum mean-free path (MFP) to study the size dependence of κ_ι. From figure 9, one can see that the total accumulation keeps increasing as MFPs increases, until reaching the plateau after MFPs increase to 64 nm and 38 nm for Bi₂O₂Se and Bi₂O₂Te, respectively. The maximum MFPs in Bi₂O₂Se and Bi₂O₂Te are much shorter than that of PbTe (about 300 nm) [40]. Furthermore, phonons with MFPs contributed about 80% of the total κ_ι are 17 nm for Bi₂O₂Se and 8.9 nm for Bi₂O₂Te. This means that the nanostructures with the length of 17 and 8.9 nm would reduce κ_l by 20% for both Bi₂O₂X. That is to say, to consequentially reduce lattice thermal conductivity of Bi₂O₂Se and Bi₂O₂Te, the size of nanostructures should below 17 nm and 8.9 nm, respectively.

Zoom In Zoom Out Reset image size

Based on above results of electronic and phonon transport coefficients, we can obtain the ZT value of Bi₂O₂X, as shown in figure 10. The calculated ZT values are close to the available experimental ones, e.g. the calculated ZT values for n-type Bi₂O₂Se are 0.006 at 300 K with the carrier concentration 2.85 × 10¹⁸ cm⁻³, and 0.042 at 500 K with the carrier concentration 2.34 × 10¹⁸ cm⁻³, which are in agreement with the experiment values of 0.007 and 0.034, respectively [17]. Figure 10 also indicates that the p-type doping is superior to the n-type doping, and the maximum of ZT value increases with increasing temperature. At 500 K, the p-type optimal ZT values can reach 0.53 and 0.62 for Bi₂O₂Se and Bi₂O₂Te, respectively. Therefore, the p-type doping is more favorable for the improvement of thermoelectric performance of Bi₂O₂X.

Zoom In Zoom Out Reset image size

Above results are all based on the SOC. Now we discuss the difference of thermoelectric performance with and without SOC. We firstly present in figure S1 (see the supplementary materials available online at stacks.iop.org/NJP/20/123014/mmedia) the calculated electronic band structure of Bi₂O₂X using the TB-mBJ potential with and without SOC. One can see that both conduction band and valence band within SOC obviously move to low energy compared to those without SOC. The SOC reduces the energy gap, from 1.15 eV to 0.87 eV for Bi₂O₂Se, and 0.36 eV to 0.21 eV for Bi₂O₂Te. Without SOC, the energy gap of 1.15 eV is close to the previous theoretical value of 1.28 eV for Bi₂O₂Se [18]. For the conduction band, the shift toward low energy is obvious. For the valence band, we compare the energy difference between the first and the second valence band valleys for Bi₂O₂Se as shown in figure S1. The energy difference Δ₂ at the X point within SOC is larger than Δ₁ without SOC for Bi₂O₂Se. There is a big energy gap Δ₃ at the Z point for Bi₂O₂Te due to the SOC. Therefore, the effect of SOC on the electronic band structure of Bi₂O₂X is obvious, and in turn, the thermoelectric performance will also be affected by the SOC.

We further calculate and compare the S, σ, S²σ and ZT with and without SOC. Figure S2 (see the supplementary materials) indicates that the SOC has an obvious influence on the p-type S of Bi₂O₂X (X = Se, Te) at 300 K for low doping concentration. When the temperature is raised to 500 K, both p-type and n-type S decrease at the low doping concentration due to the effect of SOC on the electronic structure. The calculated electrical conductivity σ in figure S3 (see the supplementary materials) shows that the values within SOC are smaller than those without SOC at the same carrier concentration. We further give in figure S4 (see the supplementary materials) the calculated power factor S²σ with and without SOC. It can be seen that the difference is small at 300 K but obvious at 500 K, especially for the p-type doping the S²σ decreases greatly. Finally, we present in figure S5 (see the supplementary materials) the calculated ZT values with and without SOC as a function of carrier concentration. The SOC has a considerable effect on the ZT values for both p-type Bi₂O₂Se and Bi₂O₂Te at 500 K, and the optimized ZT values decrease from 0.74 to 0.53 for Bi₂O₂Se, and from 0.87 to 0.62 for Bi₂O₂Te within SOC.