Quantum phase estimation of multiple eigenvalues for small-scale (noisy) experiments

It is known that any problem efficiently solvable on a quantum computer can be formulated as eigenvalue sampling of a Hamiltonian or eigenvalue sampling of a sparse unitary matrix [1]. In this sense the algorithm of quantum phase estimation (QPE) is the only quantum algorithm which can give rise to solving problems with an exponential quantum speed-up. Despite it being such a central component of many quantum algorithms, very little work has been done so far to understand what QPE in the current noisy intermediate scale quantum (NISQ) era of quantum computing [2] where quantum devices are strongly coherence-limited. QPE comes in many variants, but a large subclass of these algorithms (e.g. the semi-classical version of textbook phase estimation [3, 4], Kitaev's phase estimation [5], Heisenberg-optimized versions [6]), are executed in an iterative sequential form using controlled-U^k gates with a single ancilla qubit [7, 8] (see figure 1), or by direct measurement of the system register itself [6]. Such circuits are of practical interest in the near term when every additional qubit requires a larger chip and brings in additional experimental complexity and incoherence.

Zoom In Zoom Out Reset image size

Some of the current literature on QPE works under limiting assumptions. The first is that one does not start in an eigenstate of the Hamiltonian [9, 10]. A second limitation is that one does not take into account the (high) temporal cost of running U^k [8] for large k when optimizing phase estimation. The size and shallowness of the QPE circuit is important since, in the absence of error correction or error mitigation, one expects entropy build-up during computation. This means that circuits with large k may not be of any practical interest.

The scenario where the input state is not an eigenstate of the unitary matrix used in phase estimation is the most interesting one from the perspective of applications, and we will consider it in this work. Such an input state can be gradually projected onto an eigenstate by the phase estimation algorithm and the corresponding eigenvalue can be inferred. However, for coherence-limited low-depth circuits one may not be able to evolve sufficiently long to project well onto one of the eigenstates. This poses the question what one can still learn about eigenvalues using low-depth circuits. An important point is that it is experimentally feasible to repeat many relatively shallow experiments (or perform them in parallel on different machines). Hence we ask what the spectral-resolving power of such phase estimation circuits is, both in terms of the number of applications of the controlled-U circuit in a single experiment, and the number of times the experiment is repeated. Such repeated phase estimation experiments require classical post-processing of measurement outcomes, and we study two such algorithms for doing this. One is our adaptation of the Bayesian estimator of [10] to the multiple-eigenvalue scenario. A second is a new estimator based on a treatment of the observed measurements as a time-series, and construction of the resultant time-shift operator. This latter method is very natural for phase estimation, as one interprets the goal of phase estimation as the reconstruction of frequencies present in the output of a temporal sound signal. In fact, the time-series analysis that we develop is directly related to what are called Prony-like methods in the signal-processing literature, see e.g. [11]. The use of this classical method in quantum signal processing, including in quantum tomography [12], seems to hold great promise.

One can interpret our results as presenting a new hybrid classical-quantum algorithm for QPE. Namely, when the number of eigenstates in an input state is small, i.e. scaling polynomially with the number of qubits ${n}_{\mathrm{sys}}$, the use of our classical post-processing method shows that there is no need to run a quantum algorithm which projects onto an eigenstate to learn the eigenvalues. We show that one can extract these eigenvalues efficiently by classically post-processing the data from experiments using a single-round QPE circuits (see section 2) and classically handling $\mathrm{poly}({n}_{\mathrm{sys}})\times \mathrm{poly}({n}_{\mathrm{sys}})$ matrices. This constitutes a saving in the required depth of the quantum circuits.

The spectral-resolution power of QPE can be defined by its scaling with parameters of the experiment and the studied system. We are able to derive analytic scaling laws for the problem of estimating single eigenvalues with the time-series estimator. We find these to agree with the numerically-observed scaling of both studied estimators. For the more general situation, with multiple eigenvalues and experimental error, we study the error in estimating the lowest eigenvalue numerically. This is assisted by the low classical computation cost of both estimators. We observe scaling laws for this error in terms of the overlap between the ground and starting state (i.e. the input state of the circuit), the gap between the ground and excited states, and the coherence length of the system. In the presence of experimental noise we attempt to adjust our estimators to mitigate the induced estimation error. For depolarizing-type noise we find such compensation easy to come by, whilst for a realistic circuit-level simulation we find smaller improvements using similar techniques.

Even though our paper focuses on QPE where the phases corresponds to eigenvalues of a unitary matrix, our post-processing techniques may also be applicable to multi-parameter estimation problems in quantum optical settings. In these settings the focus is on determining an optical phase-shift [13–15] through an interferometric set-up. There is experimental work on (silicon) quantum photonic processors [16–18] on multiple-eigenvalue estimation for Hamiltonians which could also benefit from using the classical post-processing techniques that we develop in this paper.

QPE covers a family of quantum algorithms which measure a system register of ${n}_{\mathrm{sys}}$ qubits in the eigenbasis of a unitary operator U [5, 19]

$$\begin{eqnarray}&&U| {\phi }_{j}\rangle ={{\rm{e}}}^{{\rm{i}}{\phi }_{j}}| {\phi }_{j}\rangle ,\end{eqnarray} \tag{ 1 }$$

to estimate one or many phases ϕ_j. QPE algorithms assume access to a noise free quantum circuit which implements U on our system register conditioned on the state of an ancilla qubit. Explicitly, we require the ability to implement

$$\begin{eqnarray}&&{{ \mathcal U }}_{c}=| 0\rangle \langle 0| \otimes {\mathbb{I}}+| 1\rangle \langle 1| \otimes U,\end{eqnarray} \tag{ 2 }$$

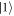where $| 0\rangle$ and $| 1\rangle$ are the computational basis states of the ancilla qubit, and ${\mathbb{I}}$ is the identity operator on the system register.

In many problems in condensed matter physics, materials science, or computational chemistry, the object of interest is the estimation of spectral properties or the lowest eigenvalue of a Hamiltonian ${\boldsymbol{ \mathcal H }}$. The eigenvalue estimation problem for ${\boldsymbol{ \mathcal H }}$ can be mapped to phase estimation for a unitary ${U}_{\tau }=\exp (-{\rm{i}}\tau {\boldsymbol{ \mathcal H }})$ with a τ chosen such that the relevant part of the eigenvalue spectrum induces phases within [−π, π). Much work has been devoted to determining the most efficient implementation of the (controlled)-$\exp (-{\rm{i}}\tau {\boldsymbol{ \mathcal H }})$ operation, using exact or approximate methods [19–22]. Alternatively, one may simulate ${\boldsymbol{ \mathcal H }}$ via a quantum walk, mapping the problem to phase estimating the unitary $\exp (-{\rm{i}}\arcsin ({\boldsymbol{ \mathcal H }})/\lambda )$ for some λ, which may be implemented exactly [23–26]. In this work we do not consider such variations, but rather focus on the error in estimating the eigenvalue phases of the unitary U that is actually implemented on the quantum computer. In particular, we focus on the problem of determining the value of a single phase ϕ₀ to high precision (this phase could correspond, for example, to the ground state energy of some Hamiltonian ${\boldsymbol{ \mathcal H }}$).

Phase estimation requires the ability to prepare an input, or starting state

$$\begin{eqnarray}&&| {\rm{\Psi }}\rangle =\displaystyle \sum _{j}{a}_{j}| {\phi }_{j}\rangle ,{A}_{j}\equiv | {a}_{j}{| }^{2},\end{eqnarray} \tag{ 3 }$$

with good overlap with the ground state; A₀ ≫ 0. Note here that the spectrum of U may have exact degeneracies (e.g. those enforced by symmetry) which phase estimation does not distinguish; we count degenerate eigenvalues as a single ϕ_j throughout this work. The ability to start QPE in a state which already has good overlap with the ground state is a non-trivial requirement for the applicability of the QPE algorithm. On the other hand, it is a well-known necessity given the QMA-completeness [27] of the lowest eigenvalue problem⁵ . For many quantum chemistry and materials science problems it is known or expected that the Hartree–Fock state has good overlap with the ground state, although rigorous results beyond perturbation theory are far and few between (see e.g. [28]). Beyond this, either adiabatic evolution [20, 29] or variational quantum eigensolvers [30] can provide an approximate starting state to improve on via phase estimation.

Phase estimation is not limited to simply learning the value of ϕ₀; it may obtain information about all phases ϕ_j as long as A_j > 0. However, the resources required to estimate ${\phi }_{j}$ are bounded below by 1/A_j. To see this, note that the controlled-unitary ${{ \mathcal U }}_{c}$ does not mix eigenstates, and so there is no difference (in the absence of error) between starting with $| {\rm{\Psi }}\rangle$ and the mixed state

$$\begin{eqnarray}&&{\rho }_{{\rm{\Psi }}}=\displaystyle \sum _{j}{A}_{j}| {\phi }_{j}\rangle \langle {\phi }_{j}| .\end{eqnarray} \tag{ 4 }$$

The latter is then equivalent to preparing the pure state $| {\phi }_{j}\rangle$ with probability A_j, so if N preparations of $| {\phi }_{j}\rangle$ are required to estimate ϕ_j to an error , the same error margin requires at least N/A_j preparations of the state $| {\rm{\Psi }}\rangle$. As the number of eigenstates ${N}_{\mathrm{eig}}$ with non-zero contribution to $| {\rm{\Psi }}\rangle$ generally scales exponentially with the system size ${n}_{\mathrm{sys}}$, estimating more than the first few ϕ_j (ordered by the magnitude A_j) will be unfeasible.

Low-cost (in terms of number of qubits) QPE may be performed by entangling the system register with a single ancilla qubit [5, 8, 10, 27]. In figure 1, we give the general form of the quantum circuit to be used throughout this paper. An experiment, labeled by a number n = 1, ..., N, can be split into one or multiple rounds r = 1, ..., R_n, following the preparation of the starting state $| {\rm{\Psi }}\rangle$. In each round a single ancilla qubit prepared in the $| +\rangle =\tfrac{1}{\sqrt{2}}(| 0\rangle +| 1\rangle )$ state controls ${{ \mathcal U }}_{c}^{{k}_{r}}$ where the integer k_r can vary per round. The ancilla qubit is then rotated by ${{ \mathcal R }}_{z}({\beta }_{r})=\exp (-{\rm{i}}{\beta }_{r}Z/2)$ (with the phase β_r possibly depending on other rounds in the same experiment) and read out in the X-basis, returning a measurement outcome m_r ∈ {0, 1}. We denote the chosen strings of integers and phases of a single multi-round experiment by k and ${\boldsymbol{\beta }}$, respectively. We denote the number of controlled-U iterations per experiment as $K={\sum }_{r=1}^{{R}_{n}}{k}_{r}$. We denote the total number of controlled-U iterations over all experiments as

$$\begin{eqnarray}&&{K}_{\mathrm{tot}}=\displaystyle \sum _{n=1}^{N}\displaystyle \sum _{r=1}^{{R}_{n}}{k}_{r}.\end{eqnarray} \tag{ 5 }$$

As the system register is held in memory during the entire time of the experiment, the choice of K is dictated by the coherence time of the underlying quantum hardware. Hence, we introduce a dimensionless coherence length

$$\begin{eqnarray}&&{K}_{\mathrm{err}}=\displaystyle \frac{{T}_{\mathrm{err}}}{{n}_{\mathrm{sys}}{T}_{U}}.\end{eqnarray} \tag{ 6 }$$

Here T_U is the time required to implement a single application of controlled-U in equation (7), and T_err is the time-to-error of a single qubit, so that ${T}_{\mathrm{err}}/{n}_{\mathrm{sys}}$ is the time-to-failure of ${n}_{\mathrm{sys}}$ qubits. The idea is that K_err bounds the maximal number of applications of U in an experiment, namely K ≤ K_err.

A new experiment starts with the same starting state $| {\rm{\Psi }}\rangle$. Values of k_r and β_r may be chosen independently for separate experiments n, i.e. we drop the label n for convenience. We further drop the subscript r from single-round experiments (with R = 1).

In the absence of error, one may calculate the action of the QPE circuit on the starting state (defined in equation (3)). Working in the eigenbasis of U on the system register, and the computational basis on the ancilla qubit, we calculate the state following the controlled-rotation ${{ \mathcal U }}_{c}^{{k}_{1}}$, and the rotation ${{ \mathcal R }}_{z}({\beta }_{1})$ on the ancilla qubit to be

$$\begin{eqnarray}&&\displaystyle \frac{1}{\sqrt{2}}\displaystyle \sum _{j}{a}_{j}\left(| 0\rangle +{{\rm{e}}}^{{\rm{i}}({k}_{1}{\phi }_{j}+{\beta }_{1})}| 1\rangle \right)| {\phi }_{j}\rangle .\end{eqnarray} \tag{ 7 }$$

The probability to measure the ancilla qubit in the X-basis as m₁ ∈ {0, 1} is then

$$\begin{eqnarray}&&\displaystyle \sum _{j}{A}_{j}{\cos }^{2}\left(\displaystyle \frac{{k}_{1}{\phi }_{j}}{2}+\displaystyle \frac{{\beta }_{1}-{m}_{1}\pi }{2}\right),\end{eqnarray} \tag{ 8 }$$

and the unnormalized post-selected state of the system register is

$$\begin{eqnarray}&&\displaystyle \sum _{j}{a}_{j}{{\rm{e}}}^{\tfrac{{\rm{i}}}{2}({k}_{1}{\phi }_{j}+{\beta }_{1})}\cos \left(\displaystyle \frac{{k}_{1}{\phi }_{j}}{2}+\displaystyle \frac{{\beta }_{1}-{m}_{1}\pi }{2}\right)| {\phi }_{j}\rangle .\end{eqnarray} \tag{ 9 }$$

The above procedure may then be repeated for r rounds to obtain the probability of a string ${\bf{m}}$ of measurement outcomes of one experiment as

$$\begin{eqnarray}&&{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})=\displaystyle \sum _{j}{A}_{j}\displaystyle \prod _{r=1}^{R}{\cos }^{2}\left(\displaystyle \frac{{k}_{r}{\phi }_{j}}{2}+\displaystyle \frac{{\beta }_{r}-{m}_{r}\pi }{2}\right).\end{eqnarray} \tag{ 10 }$$

Here, ${\boldsymbol{\phi }}$ is the vector of phases ϕ_j and ${\boldsymbol{A}}$ the vector of probabilities for different eigenstates. We note that ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ is independent of the order in which the rounds occur in the experiment. Furthermore, when ${N}_{\mathrm{eig}}=1$, ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| \phi )={P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ is equal to the product of the single-round probabilities ${P}_{{k}_{r},{\beta }_{r}}({m}_{r}| \phi )$, as there is no difference between a multi-round experiment and the same rounds repeated across individual experiments.

One can make a direct connection with parameter estimation work by considering the single-round experiment scenario in figure 1. The Hadamard gate putting the ancilla qubit in $| +\rangle$ and measuring the qubit in the X-basis are, in the optical setting, realized by beam-splitters, so that only the path denoted by the state $| 1\rangle$ will pick up an unknown phase-shift. When the induced phase-shift is not unique but depends, say, on the state of another quantum system, we may like to estimate all such possible phases corresponding to our scenario of wishing to estimate multiple eigenvalues. Another physical example is a dispersively coupled qubit-cavity mode system where the cavity mode occupation number will determine the phase accumulation of the coupled qubit [31].

Two challenges are present in determining ϕ₀ from QPE experiments. First, we only ever have inexact sampling knowledge of ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$. That is, repeated experiments at fixed ${\bf{k}},{\boldsymbol{\beta }}$ do not directly determine ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$, but rather sample from the multinomial distribution ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$. From the measurement outcomes we can try to estimate ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ (and from this ϕ₀) as a hidden variable. Secondly, when ${N}_{\mathrm{eig}}\gt 1$ determining ϕ₀ from ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ poses a non-trivial problem.

Let us first consider the case ${N}_{\mathrm{eig}}=1$. Let us assume that we do single-round experiments with a fixed k for each experiment. Naturally, taking k = 1 would give rise to the lowest-depth experiments. If we start these experiments with k = 1 in the eigenstate $| {\phi }_{0}\rangle$, then one can easily prove that taking β = 0 or $\beta =\tfrac{\pi }{2}$ for half of the experiments, suffices to estimate ϕ₀ with variance scaling as $1/N=1/{K}_{{\rm{tot}}}$. This result can be derived using standard Chernoff bounds, see e.g. [32, 33], and represent standard sampling or shot noise behavior. When ${N}_{\mathrm{eig}}=1$, N K-round experiments each with k = 1 are indistinguishable from N × K single-round experiments with k = 1. This implies that the same scaling holds for such multi-round experiments, i.e. the variance scales as $1/({NK})=1/{K}_{\mathrm{tot}}$.

Once the phase ϕ₀ is known to sufficient accuracy, performing QPE experiments with k > 1 is instrumental in resolving ϕ₀ in more detail, since the probability of a single-round outcome depends on kϕ₀ [6]. Once one knows with sufficient certainty that ${\phi }_{0}\in [(2m-1)\pi /k,(2m+1)\pi /k)$ (for integer m), one can achieve variance scaling as $1/{k}^{2}N$ (conforming to so-called local estimation Cramer–Rao bounds suggested in [10, 34]). A method achieving Heisenberg scaling, where the variance scales as $1/{K}_{{\rm{tot}}}^{2}$ (see equation (5)), was analyzed in [6, 32]. This QPE method can also be compared with the information-theoretic optimal maximum-likelihood phase estimation method of [8] where $N\sim \mathrm{log}K$ experiments are performed, each choosing a random $k\in \{1,\,\ldots ,\,K\}$ to resolve ϕ₀ with error scaling as 1/K. The upshot of these previous results is that, while the variance scaling in terms of the total number of unitaries goes like 1/K_tot when using k = 1, clever usage of k > 1 data can lead to $1/{K}_{\mathrm{tot}}^{2}$ scaling. However, as K is limited by K_err in near-term experiments, this optimal Heisenberg scaling may not be accessible.

When ${N}_{\mathrm{eig}}\gt 1$, the above challenge is complicated by the need to resolve the phase ϕ₀ from the other ϕ_j. This is analogous to the problem of resolving a single note from a chord. Repeated single-round experiments at fixed k and varying β can only give information about the value of the function:

$$\begin{eqnarray}&&g(k)=\displaystyle \sum _{j}{A}_{j}{{\rm{e}}}^{{\rm{i}}{k}{\phi }_{j}},\end{eqnarray} \tag{ 11 }$$

at this fixed k, since

$$\begin{eqnarray}\begin{array}{rcl}{P}_{k,\beta }(m| \phi ) & = & \displaystyle \frac{1}{2}+\displaystyle \frac{1}{2}\cos (\beta +m\pi )\mathrm{Re}[g(k)]\\ & & -\displaystyle \frac{1}{2}\sin (\beta +m\pi )\mathrm{Im}[g(k)].\end{array}\end{eqnarray} \tag{ 12 }$$

This implies that information from single-round experiments at fixed k is insufficient to resolve ϕ₀ when ${N}_{\mathrm{eig}}\gt 1$, as g(k) is then not an invertible function of ϕ₀ (try to recover a frequency from a sound signal at a single point in time!). In general, for multi-round experiments using a maximum of K total applications of ${{ \mathcal U }}_{c}$, we may only ever recover g(k) for k ≤ K. This can be seen from expanding ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ as a sum of ${\sum }_{j}{A}_{j}{\cos }^{m}({\phi }_{j}){\sin }^{n}({\phi }_{j})$ terms with m + n ≤ K, which are in turn linear combinations of g(k) for k ≤ K. As we will show explicitly in the next section 3.1 this allows us to recover up to K ϕ_j. However, when ${N}_{\mathrm{eig}}\gt K$, these arguments imply that we cannot recover any phases exactly. In this case, the accuracy to which we can estimate our target ϕ₀ is determined by the magnitude of the amplitude A₀ in the inital state $| {\rm{\Psi }}\rangle$ as well as the gap towards the other eigenvalues. For example, in the limit ${A}_{0}\to 1$, an unbiased estimation of ϕ₀ using data from k = 1 would be

$$\begin{eqnarray}&&\mathrm{Arg}[g(1)]=\mathrm{Im}\left[\mathrm{ln}\Space{0ex}{3.0ex}{0ex}\displaystyle \sum _{j}{A}_{j}{{\rm{e}}}^{{\rm{i}}{\phi }_{j}}\Space{0ex}{3.0ex}{0ex})\right],\end{eqnarray} \tag{ 13 }$$

and the error in such estimation is

$$\begin{eqnarray*}\begin{array}{rcl}| \mathrm{Arg}[g(1)]-{\phi }_{0}| & = & \left|\displaystyle \frac{1}{{A}_{0}}\displaystyle \sum _{j\,=\,1}^{{N}_{\mathrm{eig}}-1}{A}_{j}\sin ({\phi }_{j}-{\phi }_{0})+O({A}_{0}^{-2})\right|\\ & \leqslant & \displaystyle \frac{1-{A}_{0}}{{A}_{0}},\end{array}\end{eqnarray*}$$

with our bound being independent of ${N}_{\mathrm{eig}}$. We are unable to extend this analysis beyond the k = 1 scenario, and instead we study the scaling in this estimation numerically in section 4. In the remainder of this section, we present two estimators for multi-round QPE. The first is an estimator based on a time-series analysis of the function g(k) using Prony-like [11] methods that has a low computation overhead. The second is a Bayesian estimator similar to that of [10], but adapted for multiple eigenphases ϕ_j.

3.1. Time-series analysis

Let us assume that the function g(k) in equation (11) is a well-estimated function at all points 0 ≤ k ≤ K, since the number of experiments N is sufficiently large. We may extend this function to all points $-K\leqslant k\leqslant K$ using the identity $g(-k)={g}^{* }(k)$ to obtain a longer signal⁶ . We wish to determine the dominant frequencies ϕ_j in the signal g(k) as a function of 'time' k. This can be done by constructing and diagonalizing a time-shift matrix ${\mathfrak{T}}$ whose eigenvalues are the relevant frequencies in the signal, as follows.

We first demonstrate the existence of the time-shift matrix ${\mathfrak{T}}$ in the presence of ${N}_{\mathrm{eig}}\lt K$ separate frequencies. Since we may not know ${N}_{\mathrm{eig}}$, let us first estimate it as l. We then define the vectors ${\bf{g}}{(k)=(g(k),g(k+1),\ldots g(k+l))}^{T}$, $k=-K,\,\ldots ,\,K$. These vectors can be decomposed in terms of single-frequency vectors ${{\bf{b}}}_{j}={(1,{{\rm{e}}}^{{\rm{i}}{\phi }_{j}},\ldots ,{{\rm{e}}}^{{\rm{i}}{l}{\phi }_{j}})}^{T}$

$$\begin{eqnarray}&&{\bf{g}}(k)=\displaystyle \sum _{j}{A}_{j}{{\rm{e}}}^{{\rm{i}}{k}{\phi }_{j}}{{\bf{b}}}_{j}.\end{eqnarray} \tag{ 14 }$$

We can make a $l\times {N}_{\mathrm{eig}}$ matrix B with the components b_j as columns

$$\begin{eqnarray}&&{B}_{k,j}={{\rm{e}}}^{{\rm{i}}{k}{\phi }_{j}}.\end{eqnarray} \tag{ 15 }$$

When ${N}_{\mathrm{eig}}\leqslant l$, the columns of B are typically linearly independent⁷ , hence the non-square matrix B is invertible and has a (left)-pseudoinverse B⁻¹ such that B⁻¹B = 1. Note however, when ${N}_{\mathrm{eig}}\gt l$ the columns of B are linearly-dependent, so B cannot be inverted. If B is invertible, we can construct the shift matrix ${\mathfrak{T}}={{BDB}}^{-1}$ with ${D}_{{\rm{i}},j}={\delta }_{{\rm{i}},j}{{\rm{e}}}^{{\rm{i}}{\phi }_{j}}$. By construction, ${\mathfrak{T}}{{\bf{b}}}_{j}={{\rm{e}}}^{{\rm{i}}{\phi }_{j}}{{\bf{b}}}_{j}$ (as ${\mathfrak{T}}B={BD}$), and thus

$$\begin{eqnarray}\begin{array}{rcl}{\mathfrak{T}}{\bf{g}}(k) & = & \displaystyle \sum _{j}{A}_{j}{{\rm{e}}}^{{\rm{i}}{k}{\phi }_{j}}{\mathfrak{T}}{{\bf{b}}}_{j}\\ & = & \displaystyle \sum _{j}{A}_{j}{{\rm{e}}}^{{\rm{i}}(k+1){\phi }_{j}}={\bf{g}}(k+1).\end{array}\end{eqnarray} \tag{ 16 }$$

This implies that ${\mathfrak{T}}$ acts as the time-shift operator mapping g(k) to g(k + 1). As the eigenvalues of ${\mathfrak{T}}$ are precisely the required phases ${{\rm{e}}}^{{\rm{i}}{\phi }_{j}}$ in case ${N}_{\mathrm{eig}}\leqslant l$, constructing and diagonalizing ${\mathfrak{T}}$ will obtain our desired phases including ϕ₀. When ${N}_{\mathrm{eig}}\gt l$, the eigen-equation for ${\mathfrak{T}}$ cannot have the solution b_j since these are not linearly independent.

The above proof of existence does not give a method of constructing the time-shift operator ${\mathfrak{T}}$, as we do not have access to the matrices B or D. To construct ${\mathfrak{T}}$ from the data that we do have access to, we construct the $l\times (2K+1-l)$ Hankel matrices G⁽⁰⁾, G⁽¹⁾ by

$$\begin{eqnarray}&&{G}_{i,j}^{(a)}=g(i+j+a-K),\end{eqnarray} \tag{ 17 }$$

indexing 0 ≤ i ≤ l − 1, $0\leqslant j\leqslant 2K-l$. The kth column of G^(a) is the vector ${\bf{g}}(k+a-K)$, and so ${\mathfrak{T}}{G}^{(0)}={G}^{(1)}$. We can thus attempt to find ${\mathfrak{T}}$ as a solution of the (least-squares) problem of minimizing $| | {\mathfrak{T}}{G}^{(0)}-{G}^{(1)}| |$. The rank of the obtained $\tilde{{\mathfrak{T}}}$ is bounded by the rank of G⁽⁰⁾. We have that $\mathrm{rank}({G}^{(0)})$ is at most ${N}_{\mathrm{eig}}$ since it is a sum over rank-1 matrices. At the same time $\mathrm{rank}({G}^{(0)})\leqslant \min (l,2K+1-l)$. This implies that we require both $l\geqslant {N}_{\mathrm{eig}}$ and $2K+1-l\geqslant {N}_{\mathrm{eig}}$ to obtain a shift matrix ${\mathfrak{T}}$ with ${N}_{\mathrm{eig}}$ eigenvalues. This is only possible when $K\geqslant {N}_{\mathrm{eig}}$, giving an upper bound for the number of frequencies obtainable. When G⁽⁰⁾ is not full rank (because ${N}_{\mathrm{eig}}\lt l$), this problem may have multiple zeros $\tilde{{\mathfrak{T}}}$. However, when ${N}_{\mathrm{eig}}\lt l$ each of these must satisfy $\tilde{{\mathfrak{T}}}{\bf{g}}(k)={\bf{g}}(k+1)$ for $-K\lt k\lt K-l$.

Then, as long as $\mathrm{rank}({G}^{(0)})\geqslant {N}_{\mathrm{eig}}$, equation (14) is invertible by an operator C

$$\begin{eqnarray}&&\displaystyle \sum _{k}{C}_{i,k}{A}_{j}{{\rm{e}}}^{{\rm{i}}{k}{\phi }_{j}}={\delta }_{i,j}\to {{\bf{b}}}_{j}=\displaystyle \sum _{k}{C}_{j,k}{\bf{g}}(k).\end{eqnarray} \tag{ 18 }$$

It follows that

$$\begin{eqnarray}&&\displaystyle \sum _{k}{C}_{j,k}{\bf{g}}(k+1)=\displaystyle \sum _{k,l}{C}_{j,k}{A}_{l}{{\rm{e}}}^{{\rm{i}}{k}{\phi }_{l}}({{\rm{e}}}^{{\rm{i}}{\phi }_{l}}{{\bf{b}}}_{l})={{\rm{e}}}^{{\rm{i}}{\phi }_{j}}{{\bf{b}}}_{j},\end{eqnarray} \tag{ 19 }$$

and then

$$\begin{eqnarray}&&\tilde{{\mathfrak{T}}}{{\bf{b}}}_{j}=\displaystyle \sum _{k}{C}_{k,j}\tilde{{\mathfrak{T}}}{\bf{g}}(k)=\displaystyle \sum _{k}{C}_{k,j}{\bf{g}}(k+1)={{\rm{e}}}^{{\rm{i}}{\phi }_{j}}{{\bf{b}}}_{j},\end{eqnarray} \tag{ 20 }$$

so every $\tilde{{\mathfrak{T}}}$ obtained in this way must have eigenvalues ${{\rm{e}}}^{{\rm{i}}{\phi }_{j}}$.

The above analysis is completely independent of the coefficients A_j. However, once the eigenvalues ϕ_j are known, the matrix B (equation (15)) may be constructed, and the A_j may be recovered by a subsequent least-squares minimization of

$$\begin{eqnarray}&&| | B{\bf{A}}-{\bf{g}}(0)| | .\end{eqnarray} \tag{ 21 }$$

This allows us to identify spurious eigenvalues if $l\gt {N}_{\mathrm{eig}}$ (as these will have a corresponding zero amplitude). Numerically, we find no disadvantage to then choosing the largest l permitted by our data, namely l = K.

Assuming a sufficient number of repetitions N these arguments imply that this strategy requires that $K\geqslant {N}_{\mathrm{eig}}$ to determine all eigenvalues accurately. However, when $K\lt {N}_{\mathrm{eig}}$ there still exists a least-squares solution $\tilde{{\mathfrak{T}}}$ that minimizes $| | \tilde{{\mathfrak{T}}}{G}^{(0)}-{G}^{(1)}| |$. When A₀ ≫  1/K, we expect that $\tilde{{\mathfrak{T}}}$ should have eigenvalues ${{\rm{e}}}^{{\rm{i}}{\tilde{\phi }}_{0}}\approx {{\rm{e}}}^{{\rm{i}}{\phi }_{0}}$ that we can take as the estimator for ϕ₀; the same is true for any other ϕ_j with sufficiently large A_j. In figure 2 we show an example of convergence of this estimation for multiple eigenvalues ${\phi }_{j}$ as $K\to {N}_{\mathrm{eig}}$ in the case where g(k) is known precisely (i.e. in the absence of sampling noise). The error $| {\tilde{\phi }}_{0}-{\phi }_{0}|$ when $K\lt {N}_{\mathrm{eig}}$ depends on the eigenvalue gap above ϕ₀, as well as the relative weights A_j, as we will see in section 4.3.

Zoom In Zoom Out Reset image size

In appendix B we derive what variance can be obtained with this time-series method in the case $l={N}_{\mathrm{eig}}=1$, using single-round circuits with k = 1 up to K. Our analysis leads to the following scaling in N and K:

$$\begin{eqnarray}&&\mathrm{Var}(\phi )\propto \displaystyle \frac{1}{{K}^{2}N}.\end{eqnarray} \tag{ 22 }$$

We will compare these results to numerical simulations in section 4.1.

3.1.1. Estimating g(k)

The function g(k) cannot be estimated directly from experiments, but may instead be created as a linear combination of ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ for different values of k and β. For single-round experiments, this combination is simple to construct:

$$\begin{eqnarray}\begin{array}{rcl}g(k) & = & {P}_{k,0}(0| {\boldsymbol{\phi }},{\bf{A}})-{P}_{k,0}(1| {\boldsymbol{\phi }},{\bf{A}})\\ & & -{{\rm{i}}{P}}_{k,\tfrac{\pi }{2}}(0| {\boldsymbol{\phi }},{\bf{A}})+{{\rm{i}}{P}}_{k,\tfrac{\pi }{2}}(1| {\boldsymbol{\phi }},{\bf{A}}).\end{array}\end{eqnarray} \tag{ 23 }$$

For multi-round experiments, the combination is more complicated. In general, ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ is a linear combination of real and imaginary parts of g(l) with $l\lt K={\sum }_{r}{k}_{r}$. This combination may be constructed by writing ${\cos }^{2}(k{\phi }_{j}/2+\beta /2)$ and ${\sin }^{2}(k{\phi }_{j}/2+\beta /2)$ in terms of exponentials, and expanding. However, inverting this linear equation is a difficult task and subject to numerical imprecision. For some fixed choices of experiments, it is possible to provide an explicit expansion. Here we focus on K-round k = 1 experiments with K/2 β = 0 and K/2 $\beta =\tfrac{\pi }{2}$ final rotations during each experiment (choosing K even). The formula for ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ is independent of the order in which these rounds occur. Let us write ${\mathbb{P}}({\mathfrak{m}},{\mathfrak{n}}| {\boldsymbol{\phi }},{\bf{A}})$ as the probability of seeing both ${\mathfrak{m}}\in \{0,\,\ldots ,\,K/2\}$ outcomes with m_r = 1 in the K/2 rounds with β_r = 0 and ${\mathfrak{n}}\in \{0,\,\ldots ,\,K/2\}$ outcomes with n_r = 1 in the K/2 rounds with β_r = π/2. In other words, ${\mathfrak{m}}$, ${\mathfrak{n}}$ are the Hamming weights of the measurement vectors split into the two types of rounds described above. Then, one can prove that, for 0 ≤ k ≤ K/2:

$$\begin{eqnarray}&&g(k)=\displaystyle \sum _{m=0}^{K/2}\displaystyle \sum _{n=0}^{K/2}{\chi }_{k}({\mathfrak{m}},{\mathfrak{n}}){\mathbb{P}}({\mathfrak{m}},{\mathfrak{n}}| {\boldsymbol{\phi }},{\bf{A}}),\end{eqnarray} \tag{ 24 }$$

where

$$\begin{eqnarray}\begin{array}{rcl}{\chi }_{k}({\mathfrak{m}},{\mathfrak{n}}) & = & \displaystyle \sum _{l=0}^{k}{\left(-i\right)}^{k-l}\displaystyle \left(\genfrac{}{}{0em}{}{k}{l}\right)\\ & & \times \left[\displaystyle \sum _{{p}_{1}=0}^{\lfloor l/2\rfloor }\displaystyle \frac{\left(\genfrac{}{}{0em}{}{{\mathfrak{m}}}{2{p}_{1}}\right)\left(\genfrac{}{}{0em}{}{K/2-{\mathfrak{m}}}{l-2{p}_{1}}\right)}{\left(\genfrac{}{}{0em}{}{K/2}{l}\right)}-1\right]\\ & & \times \left[\displaystyle \sum _{{p}_{2}=0}^{\lfloor (k-l)/2\rfloor }\displaystyle \frac{\left(\genfrac{}{}{0em}{}{{\mathfrak{n}}}{2{p}_{2}}\right)\left(\genfrac{}{}{0em}{}{K/2-{\mathfrak{n}}}{k-l-2{p}_{2}}\right)}{\left(\genfrac{}{}{0em}{}{K/2}{k-l}\right)}-1\right].\end{array}\end{eqnarray} \tag{ 25 }$$

The proof of this equality can be found in appendix A.

Calculating g(k) from multi-round (k = 1) experiments contains an additional cost: combinatorial factors in equation (24) relate the variance in g(k) to the variance in ${\mathbb{P}}({\mathfrak{m}},{\mathfrak{n}}| {\boldsymbol{\phi }},{\bf{A}})$ but the combinatorial pre-factor $\displaystyle \left(\genfrac{}{}{0em}{}{k}{l}\right)$ can increase exponentially in k. This can be accounted for by replacing the least squares fit used above with a weighted least squares fit, so that one effectively relies less on the correctness of g(k) for large k. To do this, we construct the matrix ${\mathfrak{T}}$ row-wise from the rows ${{\bf{g}}}_{i}^{(1)}$ of G⁽¹⁾. That is, for the ith row ${{\mathfrak{t}}}_{i}$ we minimize

$$\begin{eqnarray}&&| | {{\mathfrak{t}}}_{i}{G}^{(0)}-{{\bf{g}}}_{i}^{(1)}| | .\end{eqnarray} \tag{ 26 }$$

This equation may be weighted by multiplying G⁽⁰⁾ and ${g}_{i}^{(1)}$ by the weight matrix

$$\begin{eqnarray}&&{w}_{j,k}^{(i)}={\delta }_{j,k}\displaystyle \frac{1}{{\sigma }_{{G}_{i,j}^{(1)}}},\end{eqnarray} \tag{ 27 }$$

where ${\sigma }_{{G}_{i,j}^{(1)}}$ is the standard deviation in our estimate of ${G}_{i,j}^{(1)}$. Note that the method of weighted least-squares is only designed to account for error in the independent variable of a least squares fit, in our case this is G⁽¹⁾. This enhanced effect of the sampling error makes the time-series analysis unstable for large K. We can analyze how this weighting alters the previous variance analysis when ${N}_{\mathrm{eig}}=1$. If we take this into account (see derivation in appendix B), we find that

$$\begin{eqnarray}&&\mathrm{Var}(\phi )\propto \displaystyle \frac{1}{{KN}},\end{eqnarray} \tag{ 28 }$$

for a time-series analysis applied to multi-round k = 1 experiments.

3.1.2. Classical computation cost

In practice, the time-series analysis can be split into three calculations; (1) estimation of ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ or ${\mathbb{P}}({\mathfrak{m}},{\mathfrak{n}}| {\boldsymbol{\phi }},{\bf{A}})$, (2) calculation of g(k) from these probabilities via equation (23) or equation (24), and (3) estimation of the phases ϕ from g(k). Clearly (2) and (3) only need to be done once for the entire set of experiments.

The estimation of the phases ϕ requires solving two least squares equations, with cost $O({l}^{2}K)$ (recalling that l is the number of frequencies to estimate, and K is the maximum known value of g(k)), and diagonalizing the time-shift matrix ${\mathfrak{T}}$ with cost O(l³). For single-round phase estimation this is the dominant calculation, as calculating g(k) from equation (23) requires simply K additions. As a result this estimator proves to be incredibly fast, able to estimate one frequency from a set of N = 10⁶ experiments of up to K = 10 000 in <100 ms, and l = 1000 frequencies from N = 10⁶ experiments with K = 1000 in <1 min. However, for multi-round phase estimation the calculation of g(k) in equation (24) scales as O(K⁴). This then dominates the calculation, requiring 30 s to calculate 50 points of g(k). (All calculations performed on a 2.4 GHz Intel i3 processor.) We note that all the above times are small fractions of the time required to generate the experimental data when N ≫ K, making this a very practical estimator for near-term experiments.

3.2. Efficient Bayesian analysis

When the starting state is the eigenstate $| {\phi }_{0}\rangle$, the problem of determining ϕ₀ based on the obtained multi-experiment data has a natural solution via Bayesian methods [10, 35]. Here we extend such Bayesian methodology to a general starting state. For computational efficiency we store a probability distribution over phases P(ϕ) using a Fourier representation of this periodic function P(ϕ) (see appendix C). This technique can also readily be applied to the case of Bayesian phase estimation applied to a single eigenstate.

A clearly information-theoretic optimal Bayesian strategy is to choose the ${\boldsymbol{\phi }}$ and ${\boldsymbol{A}}$ based on the data obtained in some N experiments [8]. After these N experiments, leading to qubit measurement outcomes ${\{{{\bf{m}}}_{i}\}}_{i=1}^{N}$, one can simply choose ${\bf{A}},{\boldsymbol{\phi }}$ which maximizes the posterior distribution:

$$\begin{eqnarray}&&{P}_{\mathrm{post}}({\boldsymbol{\phi }},{\bf{A}})=\displaystyle \frac{{P}_{\{{{\bf{k}}}_{i}\},\{{{\boldsymbol{\beta }}}_{i}\}}(\{{{\bf{m}}}_{i}\}| {\boldsymbol{\phi }},{\bf{A}})}{P(\{{{\bf{m}}}_{i}\})}{P}_{\mathrm{prior}}({\boldsymbol{\phi }},{\bf{A}}),\end{eqnarray} \tag{ 29 }$$

In other words, one chooses

$$\begin{eqnarray*}\begin{array}{rcl}({{\boldsymbol{\phi }}}_{\mathrm{opt}},{{\bf{A}}}_{\mathrm{opt}}) & = & \arg \mathop{\max }\limits_{{\boldsymbol{\phi }},{\bf{A}}}\mathrm{log}{P}_{\mathrm{post}}({\boldsymbol{\phi }},{\bf{A}})\\ & = & \arg \mathop{\max }\limits_{{\boldsymbol{\phi }},{\bf{A}}}\left[\mathrm{log}{P}_{\{{{\bf{k}}}_{i}\},\{{{\boldsymbol{\beta }}}_{i}\}}(\{{{\bf{m}}}_{i}\}| {\boldsymbol{\phi }},{\bf{A}})+\mathrm{log}{P}_{\mathrm{prior}}({\boldsymbol{\phi }},{\bf{A}})\right].\end{array}\end{eqnarray*}$$

A possible way of implementing this strategy is to (1) assume the prior distribution to be independent of A and ${\boldsymbol{\phi }}$ and (2) estimate the maximum by assuming that the derivative with respect to A and ${\boldsymbol{\phi }}$ vanishes at this maximum.

Instead of this method we update our probability distribution over ${\boldsymbol{\phi }}$ and A after each experiment. After experiment n the posterior distribution ${P}_{n}({\boldsymbol{\phi }},{\bf{A}})$ via Bayes' rule reads

$$\begin{eqnarray}&&{P}_{n}({\boldsymbol{\phi }},{\bf{A}})=\displaystyle \frac{{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})}{P({\bf{m}})}{P}_{n-1}({\boldsymbol{\phi }},{\bf{A}}).\end{eqnarray} \tag{ 30 }$$

To calculate the updates we will assume that the distribution over the phases ϕ_j and probabilities A_j are independent, that is

$$\begin{eqnarray}&&{P}_{n}({\boldsymbol{\phi }},{\bf{A}})={P}_{n}^{\mathrm{red}}({\bf{A}})\displaystyle \prod _{j=0}^{{N}_{\mathrm{eig}}-1}{P}_{n}^{j}({\phi }_{j}).\end{eqnarray} \tag{ 31 }$$

As prior distribution we take ${P}_{0}({\boldsymbol{\phi }},{\bf{A}})={P}_{\mathrm{prior}}({\bf{A}}){P}_{\mathrm{prior}}({\boldsymbol{\phi }})$ with a flat prior ${P}_{\mathrm{prior}}({\boldsymbol{\phi }})={\left(\tfrac{1}{2\pi }\right)}^{{N}_{\mathrm{eig}}}$, given the absence of a more informed choice. We take ${P}_{{\rm{p}}{\rm{r}}{\rm{i}}{\rm{o}}{\rm{r}}}({\bf{A}})={{\rm{e}}}^{-{({\bf{A}}-{{\bf{A}}}_{0})}^{2}/{2{\rm{\Sigma }}}^{2}}$, with A₀ and Σ² approximate mean and covariance matrices. We need to do this to break the symmetry of the problem, so that ${\tilde{\phi }}_{0}$ is estimating ϕ₀ and not any of the other ϕs. We numerically find that the estimator convergence is relatively independent of our choice of A₀ and Σ².

The approximation in equation (31) allows for relatively fast calculations of the Bayesian update of ${P}_{n}^{j}({\phi }_{j})$, and an approximation to the maximum-likelihood estimation of ${P}_{n}^{\mathrm{red}}({\bf{A}})$. Details of this computational implementation are given in (C1).

3.2.1. Classical computation cost

In contrast to the time-series estimator, the Bayesian estimator incurs a computational cost in processing the data from each individual experiment. On the other hand, obtaining the estimate ${\tilde{\phi }}_{0}$ for ϕ₀ is simple, once one has the probability distribution ${P}^{j=0}(\phi )$:

$$\begin{eqnarray*}&&{\tilde{\phi }}_{0}=\arg \left(\int {\rm{d}}\phi {P}^{j=0}(\phi ){{\rm{e}}}^{{\rm{i}}\phi }\right).\end{eqnarray*}$$

A key parameter here is the number of frequencies #freq stored in the Fourier representation of P(ϕ); each update requires multiplying a vector of length $\#\mathrm{freq}$ by a sparse matrix. Our approximation scheme for calculating the update to A makes this multiplication the dominant time cost of the estimation. As we argue in (C1) one requires $\#\mathrm{freq}\geqslant {K}_{\mathrm{tot}}$ to store a fully accurate representation of the probability vector. For the single-round scenario with k_r = 1, hence K_tot = N, we find a large truncation error when #freq ≪ N, and so the computation cost scales as N². In practice we find that processing the data from N < 10⁴ experiments takes seconds on a classical computer, but processing more than 10⁵ experiments becomes rapidly unfeasible.

3.3. Experiment design

Based on the considerations above we seek to compare some choices for the meta-parameters in each experiment, namely the number of rounds, and the input parameters k_r and β_r for each round.

Previous work [10, 36], which took as a starting state the eigenstate $| {\phi }_{0}\rangle$, formulated a choice of k and β, using single-round experiments and Bayesian processing, namely

$$\begin{eqnarray}&&k=\min \left(\unicode{x02308}\displaystyle \frac{1.25}{{\sigma }_{{P}_{n}^{j=0}({\phi }_{0})}}\unicode{x02309},{K}_{\mathrm{err}}\right),\hspace{0.5cm}\beta \sim {P}_{n}^{j=0}({\phi }_{0}=\beta ),\end{eqnarray} \tag{ 32 }$$

Roughly, this heuristic adapts to the expected noise in the circuit by not using any k such that the implementation of U^k takes longer than ${T}_{\mathrm{err}}/{n}_{\mathrm{sys}}$. It also adapts k to the standard-deviation of the current posterior probability distribution over ${\phi }_{0}$: a small standard-deviation after the nth experiment implies that k should be chosen large to resolve the remaining bits in the binary expansion of ϕ₀⁸ .

In this work we use a starting state which is not an eigenstate, and as such we must adjust the choice in equation (32). As noted in section 3, to separate different frequency contributions to g(k) we need good accuracy beyond that at a single value of k. The optimal choice of the number of frequencies to estimate depends on the distribution of the A_j, which may not be well known in advance. Following the inspiration of [10], we choose for the Bayesian estimator

$$\begin{eqnarray}\begin{array}{rcl}k & \in & \{1,\,\ldots ,\,K\}\\ K & = & \min \left(\unicode{x02308}\displaystyle \frac{1.25}{{\sigma }_{{P}_{n}^{j=0}({\phi }_{0})}}\unicode{x02309},{K}_{\mathrm{err}}\right).\end{array}\end{eqnarray} \tag{ 33 }$$

We thus similarly bound K depending how well one has already converged to a value for ϕ₀ which constitutes some saving of resources. At large N we numerically find little difference between choosing k at random from {1, ..., K} and cycling through k = 1, ..., K in order. For this Bayesian estimator we draw β at random from a uniform distribution [0, 2π). We find that the choice of β has no effect on the final estimation (as long as it is not chosen to be a single number) For the time-series estimator applied to single-round experiments, we choose to cycle over k = 1, ..., K so that it obtains a complete estimate of g(k) as soon as possible, taking an equal number of experiments with final rotation β = 0 and β = π/2 at each k. Here again K ≤ K_err, so that we choose the same number of experiments for each k ≤ K. For the time-series estimator applied to multi-round experiments, we choose an equal number of rounds with β = 0 and β = π/2, taking the total number of rounds equal to R = K.

We first focus on the performance of our estimators in the absence of experimental noise, to compare their relative performance and check the analytic predictions in section 3.1. Although with a noiseless experiment our limit for K is technically infinite, we limit it to a make connection with the noisy results of the following section. Throughout this section we generate results directly by calculating the function ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ and sampling from it. Note that ${P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}})$ only depends on ${N}_{\mathrm{eig}}$ and not on the number of qubits in the system.

4.1. Single eigenvalues

To confirm that our estimators achieve the scaling bounds discussed previously, we first test them on the single eigenvalue scenario ${N}_{\mathrm{eig}}=1$. In figure 3, we plot the scaling of the average absolute error in an estimation $\tilde{\phi }$ of a single eigenvalue ϕ ∈ [−π, π), defined so as to respect the 2π-periodicity of the phase:

$$\begin{eqnarray}&&\epsilon := \left\langle \min \left(| \phi -\tilde{\phi }| ,2\pi -| \phi -\tilde{\phi }| \right)\right\rangle =\left\langle \left|\mathrm{Arg}\left({{\rm{e}}}^{{\rm{i}}(\phi -\tilde{\phi })}\right)\right|\right\rangle ,\end{eqnarray} \tag{ 34 }$$

as a function of varying N and K. Here $\langle \rangle$ represents an average over repeated QPE simulations, and the Arg function is defined using the range [−π, π) (otherwise the equality does not hold).

Zoom In Zoom Out Reset image size

We see that both estimators achieve the previously-derived bounds in 3.1 (overlayed as dashed lines), and both estimators achieve almost identical convergence rates. The results for the Bayesian estimation match the scaling observed in [10]. Due to the worse scaling in K, the multi-round k = 1 estimation significantly underperforms single-round phase estimation. This is a key observation of this paper, showing that if the goal is to estimate a phase rather than to project onto an eigenstate, it is preferable to do single-round experiments.

4.2. Example behavior with multiple eigenvalues

The performance of QPE is dependent on both the estimation technique and the system being estimated. Before studying the system dependence, we first demonstrate that our estimators continue to perform at all in the presence of multiple eigenvalues. In figure 4, we demonstrate the convergence of both the Bayesian and time-series estimators in the estimation of a single eigenvalue ϕ₀ = −0.5 of a fixed unitary U, given a starting state $| {{\rm{\Psi }}}_{0}\rangle$ which is a linear combination of 10 eigenstates $| {\phi }_{j}\rangle$. We fix $| \langle {\phi }_{0}| {{\rm{\Psi }}}_{0}\rangle {| }^{2}=0.5$, and draw other eigenvalues and amplitudes at random from [0, π] (making the minimium gap ϕ_j − ϕ₀ equal to 0.5). We perform 2000 QPE simulations with K = 50, and calculate the mean absolute error (equation (35), solid), Holevo variance ${\left|,\left\langle {{\rm{e}}}^{{\rm{i}}\tilde{\phi }}\right\rangle ,\right|}^{-2}-1$ (dashed), and root mean squared error ${\epsilon }_{{\rm{r}}{\rm{m}}{\rm{s}}}$ (dotted), given by

$$\begin{eqnarray}&&{\epsilon }_{{\rm{r}}{\rm{m}}{\rm{s}}}^{2}:= \left\langle \min {\left(| \phi -\tilde{\phi }| ,2\pi -| \phi -\tilde{\phi }| \right)}^{2}\right\rangle =\left\langle {\left|\mathrm{Arg}\left({{\rm{e}}}^{{\rm{i}}(\phi -\tilde{\phi })}\right)\right|}^{2}\right\rangle .\end{eqnarray} \tag{ 35 }$$

We observe that both estimators retain their expected $\epsilon \propto {N}^{-1/2}$, with one important exception. The Bayesian estimator occasionally (10% of simulations) estimates multiple eigenvalues near ϕ₀. When this occurs, the estimations tend to repulse each other, making neither a good estimation of the target. This is easily diagnosable without knowledge of the true value of ϕ₀ by inspecting the gap between estimated eigenvalues. While using this data to improve estimation is a clear target for future research, for now we have opted to reject simulations where such clustering occurs (in particular, we have rejected data points where $\min ({\bar{\phi }}_{0}-{\bar{\phi }}_{j})\lt 0.05$). That this is required is entirely system-dependent: we find the physical Hamiltonians studied later in this text to not experience this effect. We attribute this difference to the distribution of the amplitudes A_j—physical Hamiltonians tend to have a few large A_j, whilst in this simulation the A_j were distributed uniformly.

Zoom In Zoom Out Reset image size

In the inset to figure 4, we plot a histogram of the estimated eigenphases after N = 10⁴ experiments. For the Bayesian estimator, we show both the selected (green) and rejected (blue) eigenphases. We see that regardless of whether rejection is used, the distribution appears symmetric about the target phase ϕ₀. This suggests that in the absence of experimental noise, both estimators are unbiased. Proving this definitively for any class of systems is difficult, but we expect both estimators to be unbiased provided A₀ ≫ 1/K. When A₀ ≤ 1/K, one can easily construct systems for which no phase estimation can provide an unbiased estimation of ϕ₀ (following the arguments of section 3). We further see that the scaling of the rms error _rms and the Holevo variance match the behavior of the mean absolute error , implying that our results are not biased by the choice of estimator used.

4.3. Estimator scaling with two eigenvalues

The ability of QPE to resolve separate eigenvalues at small K can be tested in a simple scenario of two eigenvalues, ϕ₀ and ϕ₁. The input to the QPE procedure is then entirely characterized by the overlap A₀ with the target state $| {\phi }_{0}\rangle$, and the gap $\delta =| {\phi }_{0}-{\phi }_{1}|$.

In figure 5, we study the performance of our time-series estimator in estimating ϕ₀ after N = 10⁶ experiments with K = 50, measured again by the mean error (equation (35)). We show a two-dimensional plot (averaged over 500 simulations at each point A₀, δ) and log–log plots of one-dimensional vertical (lower left) and horizontal (lower right) cuts through this surface. Due to computational costs, we are unable to perform this analysis with the Bayesian estimator, or for the multi-round scenario. We expect the Bayesian estimator to have similar performance to the time-series estimator (given their close comparison in sections 4.1 and 4.2). We also expect the error in multi-round QPE to follow similar scaling laws in A₀ and δ as single-round QPE (i.e. multi-round QPE should be suboptimal only in its scaling in K).

Zoom In Zoom Out Reset image size

The ability of our estimator to estimate ϕ₀ in the presence of two eigenvalues can be split into three regions (marked as (a), (b), (c) on the surface plot). In region (a), we have performed insufficient sampling to resolve the eigenvalues ϕ₀ and ϕ₁, and QPE instead estimates the weighted average phase ${A}_{0}{\phi }_{0}+{A}_{1}{\phi }_{1}$. The error in the estimation of ϕ₀ then scales by how far it is from the average, and how well the average is resolved

$$\begin{eqnarray}&&\epsilon \propto (1-{A}_{0})\delta {K}^{-1}{N}^{-1/2}.\end{eqnarray} \tag{ 36 }$$

In region (b), we begin to separate ϕ₀, from the unwanted frequency ϕ₁, and our convergence halts

$$\begin{eqnarray}&&\epsilon \propto {A}_{0}^{-1}{\delta }^{-2}.\end{eqnarray} \tag{ 37 }$$

In region (c), the gap is sufficiently well resolved and our estimation returns to scaling well with N and K

$$\begin{eqnarray}&&\epsilon \propto {A}_{0}^{-1}{K}^{-1}{N}^{-1/2}.\end{eqnarray} \tag{ 38 }$$

The scaling laws in all three regions can be observed in the various cuts in the lower plots of figure 5. We note that the transition between the three regions is not sharp (boundaries estimated by hand), and is K and N-dependent.

4.4. Many eigenvalues

To show that our observed scaling is applicable beyond the toy 2-eigenvalue system, we now shift to studying systems of random eigenvalues with ${N}_{\mathrm{eig}}\gt 1$. In keeping with our insight from the previous section, in figure 6 we fix ϕ₀ = 0, and study the error as a function of the gap

$$\begin{eqnarray}&&\delta =\mathop{\min }\limits_{j\gt 1}(| {\phi }_{j}-{\phi }_{0}| ).\end{eqnarray} \tag{ 39 }$$

We fix A₀ = 0.5, and draw the other parameters for the system from a uniform distribution: ϕ_j ∼ [δ, π], A_j ∼ [0, 0.5] (fixing ${\sum }_{j=1}^{{N}_{\mathrm{eig}}}{A}_{j}=1-{A}_{0}$). We plot both the average error (line) and the upper 47.5% confidence interval [,  + 2σ] (shaded region) for various choices of ${N}_{\mathrm{eig}}$. We observe that increasing the number of spurious eigenvalues does not critically affect the error in estimation; indeed the error generally decreases as a function of the number of eigenvalues. This makes sense; at large ${N}_{\mathrm{eig}}$ the majority of eigenvalues sit in region (c) of figure 5, and we do not expect these to combine to distort the estimation. Then, the nearest eigenvalue ${\min }_{j\ne 0}{\phi }_{j}$ has on average an overlap ${A}_{j}\propto 1/{N}_{\mathrm{eig}}$, and its average contribution to the error in estimating ϕ₀ (inasmuch as this can be split into individual contributions) scales accordingly. We further note that the worst-case error remains that of two eigenvalues at the crossover between regions (a) and (b). In appendix D we study the effect of confining the spurious eigenvalues to a region $[\delta ,{\phi }_{\max }]$. We observe that when most eigenvalues are confined to regions (a) and (b), the scaling laws observed in the previous section break down, however the worst-case behavior remains that of a single spurious eigenvalue. This implies that sufficiently long K is not a requirement for QPE, even in the presence of large systems or small gaps δ; it can be substituted by sufficient repetition of experiments. However, we do require that the ground state is guaranteed to have sufficient overlap with the starting state—A₀ > 1/K (as argued in section 3). As QPE performance scales better with K than it does with N, a quantum computer with coherence time $2T$ is still preferable to two quantum computers with coherence time T (assuming no coherent link between the two).

Zoom In Zoom Out Reset image size

Experimental noise currently poses the largest impediment to useful computation on current quantum devices. As we suggested before, experimental noise limits K so that for $K\gtrsim {K}_{\mathrm{err}}$ the circuit is unlikely to produce reliable results. However, noise on quantum devices comes in various flavors, which can have different corrupting effects on the computation. Some of these corrupting effects (in particular, systematic errors) may be compensated for with good knowledge of the noise model. For example, if we knew that our system applied $U={{\rm{e}}}^{-{\rm{i}}{\boldsymbol{ \mathcal H }}(t+\epsilon )}$ instead of $U={{\rm{e}}}^{-{\rm{i}}{\boldsymbol{ \mathcal H }}t}$, one could divide $\tilde{{\phi }_{0}}$ by (t + )/t to precisely cancel out this effect. In this study we have limited ourselves to studying and attempting to correct two types of noise: depolarizing noise, and circuit-level simulations of superconducting qubits. Given the different effects observed, extending our results to other noise channels is a clear direction for future research. In this section we do not study multi-round QPE, so each experiment consists of a single round. A clear advantage of the single-round method is that the only relevant effect of any noise in a single-round experiment is to change the outcome of the ancilla qubit, independent of the number of system qubits ${n}_{\mathrm{sys}}$.

5.1. Depolarizing noise

A very simple noise model is that of depolarizing noise, where the outcome of each experiment is either correct with some probability p or gives a completely random bit with probability $1-p$. We expect this probability p to depend on the circuit time and thus the choice of k ≥ 0, i.e.

$$\begin{eqnarray}&&p=p(k)={{\rm{e}}}^{-k/{K}_{\mathrm{err}}}.\end{eqnarray} \tag{ 40 }$$

We can simulate this noise by directly applying it to the calculated probabilities ${P}_{k,\beta }(m| \phi )$ for a single round

$$\begin{eqnarray}&&{P}_{k,\beta }(m| \phi )\to {P}_{k,\beta }(m| \phi )p(k)+\displaystyle \frac{1-p(k)}{2}.\end{eqnarray} \tag{ 41 }$$

In figure 7, we plot the convergence of the time-series (blue) and Bayesian (green) estimators as used in the previous section as a function of the number of experiments, with fixed $K=50={K}_{\mathrm{err}}/2$ fixed, A₀ = 0.5, ${N}_{\mathrm{eig}}=10$ and δ = 0.5. We see that both estimators obey N^−1/2 scaling for some portion of the experiment, however this convergence is unstable, and stops beyond some critical point.

Zoom In Zoom Out Reset image size

Both the Bayesian and time-series estimator can be adapted rather easily to compensate for this depolarizing channel. To adapt the time-series analysis, we note that the effect of depolarizing noise is to send $g(k)\to g(k)p(k)$ when k > 0, via equation (23) and equation (41). Our time-series analysis was previously performed over the range $k=-K,\,\ldots ,\,K$ (getting $g(-k)={g}^{* }(k)$ for free), and over this range

$$\begin{eqnarray}&&g(k)\to g(k)p(| k| ).\end{eqnarray} \tag{ 42 }$$

g(k) is no longer a sum of exponential functions over our interval $[-K,K]$, as it is not differentiable at k = 0, which is the reason for the failure of our time-series analysis. However, over the interval [0, K] this is not an issue, and the time-series analysis may still be performed. If we construct a shift operator T using g(k) from k = 0, ..., K, this operator will have eigenvalues ${{\rm{e}}}^{{\rm{i}}{\phi }_{j}-1/{K}_{\mathrm{err}}}$. This then implies that the translation operator T can be calculated using g(k) with k > 0, and the complex argument of the eigenvalues of T give the correct phases ϕ_j. We see that this is indeed the case in figure 7 (orange line). Halving the range of g(k) that we use to estimate ϕ₀ decreases the estimator performance by a constant factor, but this can be compensated for by increasing N.

Adapting the Bayesian estimator requires simply that we use the correct conditional probability, equation (41). This in turn requires that we either have prior knowledge of the error rate K_err, or estimate it alongside the phases ϕ_j. For simplicity, we opt to choose the former. In an experiment K_err can be estimated via standard QCVV techniques, and we do not observe significant changes in estimator performance when it is detuned. Our Fourier representation of the probability distribution of ϕ₀ can be easily adjusted to this change. The results obtained using this compensation are shown in figure 7: we observe that the data follows a N^−1/2 scaling again.

5.2. Realistic circuit-level noise

Errors in real quantum computers occur at a circuit-level, where individual gates or qubits get corrupted via various error channels. To make connection to current experiments, we investigate our estimation performance on an error model of superconducting qubits. Full simulation details can be found in appendix E. Our error model is primarily dominated by T₁ and T₂ decoherence, incoherent two-qubit flux noise, and dephasing during single-qubit gates. We treat the decoherence time T_err = T₁ = T₂ as a free scale parameter to adjust throughout our simulations, whilst keeping all other error parameters tied to this single scale parameter for simplicity. In order to apply circuit-level noise we must run quantum circuit simulations, for which we use the quantumsim density matrix simulator first introduced in [37]. We then choose to simulate estimating the ground state energy of four hydrogen atoms in varying rectangular geometries, with Hamiltonian ${\boldsymbol{ \mathcal H }}$ taken in the STO-3G basis calculated via psi4 [38], requiring ${n}_{\mathrm{sys}}=8$ qubits. We make this estimation via a lowest-order Suzuki-Trotter approximation [39] to the time-evolution operator ${{\rm{e}}}^{-{\rm{i}}{\boldsymbol{ \mathcal H }}t}$. To prevent energy eigenvalues wrapping around the circle we fix $t=1/\sqrt{\mathrm{Trace}[{{\boldsymbol{ \mathcal H }}}^{\dagger }{\boldsymbol{ \mathcal H }}]/({2}^{{n}_{\mathrm{sys}}})}$ ⁹ . The resultant 9-qubit circuit is made using the OpenFermion package [9].

In lieu of any circuit optimizations (e.g. [23, 40]), the resulting circuit has a temporal length per unitary of ${T}_{U}=42\,\mu {\rm{s}}$ (with single- (two-) qubit gate times 20 ns (40 ns)). This makes the circuit unrealistic to operate at current decoherence times for superconducting circuits, and we focus on decoherence times 1−2 orders of magnitude above what is currently feasible, i.e. T_err = 5−50 ms. However one may anticipate that the ratio T_U/T_err can be enlarged by circuit optimization or qubit improvement. Naturally, choosing a smaller system, less than 8 qubits, or using error mitigation techniques could also be useful.

We observe realistic noise to have a somewhat different effect on both estimators than a depolarizing channel. Compared to the depolarizing noise, the noise may (1) be biased towards 0 or 1 and/or (2) its dependence on k may not have the form of equation (40).

In figure 8, we plot the performance of both estimators at four different noise levels (and a noiseless simulation to compare), in the absence of any attempts to compensate for the noise. Unlike for the depolarizing channel, where a N^−1/2 convergence was observed for some time before the estimator became unstable, here we see both instabilities and a loss of the N^−1/2 decay to begin with. Despite this, we note that reasonable convergence (to within 1%−2%) is achieved, even at relatively low coherence times such as K_err = 10. Regardless, the lack of eventual convergence to zero error is worrying, and we now shift to investigating how well it can be improved for either estimator.

Zoom In Zoom Out Reset image size

Adjusting the time-series estimator to use only g(k) for positive k gives approximately 1−2 orders of magnitude improvement. In figure 9, we plot the estimator convergence with this method. We observe that the estimator is no longer unstable, but the N^−1/2 convergence is never properly regained. We may study this convergence in greater deal for this estimator, as we may extract g(k) directly from our density-matrix simulations, and thus investigate the estimator performance in the absence of sampling noise (crosses on screen). We note that similar extrapolations in the absence of noise, or in the presence of depolarizing noise (when compensated) give an error rate of around 10⁻¹⁰, which we associate to fixed-point error in the solution to the least squares problem (this is also observed in the curve without noise in figure 9). Plotting this error as a function of K_err shows a power-law decay - $\epsilon \propto {K}_{\mathrm{err}}^{-\alpha }\propto {T}_{\mathrm{err}}^{-\alpha }$ with $\alpha =1.9\approx 2$. We do not have a good understanding of the source of the obtained power law.

Zoom In Zoom Out Reset image size

The same compensation techniques that restored the performance of the Bayesian estimator in the presence of depolarizing noise do not work nearly as well for realistic noise. Most likely this is due to the fact that the actual noise is not captured by a k-dependent depolarizing probability. In figure 10 we plot the results of using a Bayesian estimator when attempting to compensate for circuit-level noise by approximating it as a depolarizing channel with a decay rate (equation (40)) of ${K}_{\mathrm{err}}={T}_{\mathrm{err}}/{T}_{U}{n}_{\mathrm{sys}}$. This can be compared with the results of figure 8 where this compensation is not attempted. We observe a factor 2 improvement at low T_err, however the N^−1/2 scaling is not regained, and indeed the estimator performance appears to saturate at roughly this point. Furthermore, at T_err = 50 ms, the compensation techniques do not improve the estimator, and indeed appear to make it more unstable.

Zoom In Zoom Out Reset image size

To investigate this further, in figure 10 (inset) we plot a Bayes factor analysis of the Bayesian estimators with and without compensation techniques. The Bayes factor analysis is obtained by calculating the Bayes factors

$$\begin{eqnarray}&&F=\displaystyle \prod _{\mathrm{expt}\ n}\displaystyle \frac{P({m}_{n}| M)}{P({m}_{n}| {M}_{0})},\end{eqnarray} \tag{ 43 }$$

where M is the chosen Bayesian model (including the prior knowledge), and M₀ is a reference model, and $P(m| M)$ is the probability of observing measurement m given model M. As a reference model we take that of random noise—$P(m| {M}_{0})=0.5$. We observe that at large T_err the Bayes factor with compensation falls below that without, implying that the compensation techniques make the model worse. We also observe that at very small T_err, the estimator makes worse predictions than random noise ($\mathrm{log}(F)\lt 0$). Despite our best efforts we have been unable to further improve the Bayesian estimator in noisy single-round QPE experiments.

In this work, we have presented and studied the performance of two estimators for QPE at low K for different experiment protocols, different systems (in particular those with one versus many eigenvalues), and under simplistic and realistic noise conditions. These findings are summarized in table 1. From our numerical studies, we observe scaling laws for our time-series estimator; we find it first-order sensitive to the overlap A₀ between starting state and ground state, second-order sensitive to the gap between the ground state and the nearest eigenstates, and second-order sensitive to the coherence time of the system. The Bayesian estimator appears to perform comparably to the time-series estimator in all circumstances, and thus should obey similar scaling laws.

Table 1.  Table comparing metrics of interest between the two studied estimators. All metrics are implementation-specific, and may be improvable.

	Time-series estimator	Bayesian estimator
Speed (scaling)	O(K)	O(N2)
Speed (timing)	Processes large datasets in milliseconds	Takes hours to process 105 experiments
Accuracy	$\epsilon \propto {N}^{-1/2}{K}^{-1}{A}_{0}^{-1}{\delta }^{-2}$demonstrated.	$\epsilon \propto {N}^{-1/2}{K}^{-1}$ demonstrated $\epsilon \propto {A}_{0}^{-1}{\delta }^{-2}$ expected.
Number of eigenvalues estimated	100−200 with relative ease	Limited to 2−5
Improve accuracy via classical approximation	Not obvious	Can get speedup via choice of prior (not attempted in this work)
Account for error	Limited ability	Limited ability

We further observe that realistic noise has a worse effect on QPE than a depolarizing channel, for which the effects can largely be mitigated. We have numerically explored (but not reported) multi-round QPE in the presence of noise. Since each experiment has multiple outputs, it is harder to adapt the classical data analysis to the presence of noise and our results for realistic noise have not been convincing so far. Since the performance of multi-round noiseless QPE is already inferior to single-round noiseless QPE, we do not advocate it as a near-term solution, although, for noiseless long circuits it does have the ability to project onto a single eigenstate, which single-round QPE certainly does not.

Despite our slightly pessimistic view of the effect of errors on the performance of QPE, we should note that the obtained error of 10⁻³ at ${T}_{\mathrm{err}}\approx 13{n}_{\mathrm{sys}}{T}_{U}$ or K_err = 13 would be sufficient to achieve chemical accuracy in a small system. However, as the energy of a system scales with the number of particles, if we require a Hamiltonian's spectrum to fit in $[-\pi ,\pi )$, we will need a higher resolution for QPE, making error rates of 10⁻³ potentially too large. This could potentially be improved by improving the compensation techniques described in the text, applying error mitigation techniques to effectively increase T_err, or by using more well-informed prior distributions in the Bayesian estimator to improve accuracy. All of the above are obvious directions for future work in optimizing QPE for the NISQ era. Another possible direction is to investigate QPE performance in other error models than the two studied here. Following [6], we expect SPAM errors to be as innocuous as depolarizing noise. However, coherent errors can be particularly worrying as they imitate alterations to the unitary U. The time-series estimator is a clear candidate for such a study, due to its ease in processing a large number of experiments and its ability to be studied in the absence of sampling noise. We also expect that it is possible to combine the time-series estimator with the Heisenberg-limited scaling methods of [6, 32] so as to extend these optimal methods to the multiple-eigenvalue scenario with ${N}_{\mathrm{eig}}\gt 1$ eigenvalues, and that these methods could be extended to analog or ancilla-free QPE settings such as described in [6].

In this work we do not compare the performance of QPE with purely classical methods. Let us assume that we have a classical efficient representation of the starting state Ψ and one can efficiently calculate $\mathrm{Tr}{{\boldsymbol{ \mathcal H }}}^{k}| {\rm{\Psi }}\rangle \langle {\rm{\Psi }}|$ for k = 1, ..., K with K = O(1) (for fermionic Gaussian starting states and fermionic Hamiltonians this is possible as a single fermionic term in ${{\boldsymbol{ \mathcal H }}}^{k}$ can be estimated as the Pfaffian of some matrix). Then, if there are at most K = O(1) eigenstates in this initial state, the time-series method would allow us to extract these eigenvalues efficiently. Thus in this setting and under these assumptions QPE would not offer an exponential computational advantage.

The authors would like to thank Viacheslav Ostroukh for assistance with quantum simulation, Lucas Visscher for assistance with molecular simulation, Chris Granade for advice on Bayesian techniques, Detlef Hohl and Shell for useful discussions, and Carlo Beenakker, Leonardo DiCarlo, Nathan Wiebe, Ryan Babbush, Jarrod McClean, Yuval Sanders, Xavier Bonet, Sonika Johri and Francesco Buda for advice and feedback on the project. The work by TE O'Brien was supported by the Netherlands Organization for Scientific Research (NWO/OCW) and an ERC Synergy grant. The work by BM Terhal was supported by ERC grant EQEC No. 682726. The work by B Tarasinski was supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the US Army Research Office grant W911NF-16-1-0071. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the ODNI, IARPA, or the US Government. The US Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon.

One first writes for 0 ≤ k ≤ K/2:

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \sum _{j}{A}_{j}\exp ({\rm{i}}{k}{\phi }_{j}) & = & \displaystyle \sum _{{\bf{m}},{\bf{n}}}{{\rm{\Pi }}}_{i=1}^{k}[{\left(-1\right)}^{{m}_{i}}-{\rm{i}}{\left(-1\right)}^{{n}_{i}}]\\ & & \times {\mathbb{P}}({m}_{1},\,\ldots ,\,{m}_{K/2},{n}_{1},\ldots {n}_{K/2}| {\boldsymbol{\phi }},{\bf{A}}),\end{array}\end{eqnarray} \tag{ A1 }$$

where ${\mathbb{P}}({m}_{1},\,\ldots ,\,{m}_{K/2},{n}_{1},\ldots {n}_{K/2}| {\boldsymbol{\phi }},{\bf{A}})$ is the probability for a specific series of outcomes m₁, ..., m_K/2 for β = 0 and n₁, ..., n_K/2 for β = π/2. To see that the above is true, note that it is quickly true for ${N}_{\mathrm{eig}}=1$ by using equation (23) for g(1). By linearity on the left and right-hand side it then holds generally.

Since the order of the outcomes of the rounds does not matter, i.e. ${\mathbb{P}}({m}_{1},\,\ldots ,\,{m}_{K/2},{n}_{1},\ldots {n}_{K/2}| {\boldsymbol{\phi }},{\bf{A}})$ only depends on the Hamming weights ${\mathfrak{m}}=| {\bf{m}}|$ and ${\mathfrak{n}}=| {\bf{n}}|$, we can symmetrize the coefficient over permutations of the rounds and replace ${\mathbb{P}}({m}_{1},\,\ldots ,\,{m}_{K/2},{n}_{1},\ldots {n}_{K/2}| {\boldsymbol{\phi }},{\bf{A}})$ by ${\mathbb{P}}\left({\mathfrak{m}},{\mathfrak{n}}| {\boldsymbol{\phi }},{\bf{A}}\right)/\left(\displaystyle \left(\genfrac{}{}{0em}{}{K/2}{{\mathfrak{m}}}\right)\displaystyle \left(\genfrac{}{}{0em}{}{K/2}{{\mathfrak{n}}}\right)\right)$. This gives the following expression for ${\chi }_{k}({\mathfrak{m}},{\mathfrak{n}})$ :

$$\begin{eqnarray*}\begin{array}{rcl}{\chi }_{k}({\mathfrak{m}},{\mathfrak{n}}) & = & \displaystyle \frac{1}{{\left((K/2)!\right)}^{2}}\displaystyle \sum _{{\pi }_{1}\in {S}_{K/2},{\pi }_{2}\in {S}_{K/2}}\displaystyle \prod _{i=1}^{k}({\left(-1\right)}^{{m}_{{\pi }_{1}(i)}}-i{\left(-1\right)}^{{n}_{{\pi }_{2}(i)}}),\end{array}\end{eqnarray*}$$

where m_i is the ith bit of a bitstring with Hamming weight ${\mathfrak{m}}$ (and similarly n_i), and S_K/2 is the symmetric group of permutations. We can expand this last expression as

$$\begin{eqnarray*}\begin{array}{rcl}{\chi }_{k}({\mathfrak{m}},{\mathfrak{n}}) & = & \displaystyle \sum _{k=0}^{l}\displaystyle \left(\genfrac{}{}{0em}{}{k}{l}\right){\left(-i\right)}^{k-l}\rho (l,{\mathfrak{m}})\rho (k-l,{\mathfrak{n}})\\ \rho (l,{\mathfrak{m}}) & = & \displaystyle \frac{1}{(K/2)!}\displaystyle \sum _{\pi }{\left(-1\right)}^{{m}_{\pi (1)}}\ldots {\left(-1\right)}^{{m}_{\pi (l)}}\\ & = & -1+\displaystyle \frac{2}{(K/2)!}\displaystyle \sum _{\pi :{m}_{\pi (1)}\ldots {m}_{\pi (l)}{\rm{is}}\,{\rm{even}}}1.\end{array}\end{eqnarray*}$$

The sum ${\sum }_{\pi :{m}_{\pi (1)}\ldots {m}_{\pi (l)}{\rm{is}}{\rm{even}}}$ can be written as a sum over permutations such that ${m}_{\pi (1)}\ldots {m}_{\pi (l)}$ has Hamming weight $2p$ with $p=0,1,\ldots \lfloor l/2\rfloor$. Then one counts the number of permutations of a K/2-bitstring of Hamming weight ${\mathfrak{m}}$ such that some segment of length l has Hamming weight $2p$ which equals $\displaystyle \left(\genfrac{}{}{0em}{}{{\mathfrak{m}}}{2p}\right)\displaystyle \left(\genfrac{}{}{0em}{}{K/2-{\mathfrak{m}}}{l-2p}\right)\ l!\ (K/2-l)!$. All together this leads to ${\chi }_{k}({\mathfrak{m}},{\mathfrak{n}})$ in equation (25). It is not clear whether one can simplify this equality or verify it directly using other combinatorial identities or (Chebyshev) polynomials.

For the case of estimating a single eigenvalue using single-round QPE with the time-series estimator, one can directly calculate the error in the estimation. In this situation, our matrices G₀ and G₁ are column vectors

$$\begin{eqnarray}&&{G}_{0}^{T}=(g(-K),g(-K+1),\,\ldots ,\,g(K-1)),\end{eqnarray} \tag{ B1 }$$

$$\begin{eqnarray}&&{G}_{1}^{T}=(g(-K+1),g(-K+2),\,\ldots ,\,g(K)).\end{eqnarray} \tag{ B2 }$$

The least-squares solution for ${\mathfrak{T}}$ is then

$$\begin{eqnarray}&&{\mathfrak{T}}={\left({G}_{0}^{\dagger }{G}_{0}\right)}^{-1}{G}_{0}^{\dagger }{G}_{1}=\displaystyle \frac{{\displaystyle \sum }_{k=-K}^{K-1}{g}^{* }(k)g(k+1)}{{\displaystyle \sum }_{k=-K}^{K-1}{g}^{* }(k)g(k)}.\end{eqnarray} \tag{ B3 }$$

For a single frequency, $g(k)={{\rm{e}}}^{{\rm{i}}{k}\phi }$, and immediately ${\mathfrak{T}}={{\rm{e}}}^{{\rm{i}}\phi }$. However, we estimate the real and imaginary components of g(k) separately. Let us write in terms of our independent components

$$\begin{eqnarray}&&{\mathfrak{T}}={{\mathfrak{T}}}_{r}+{\rm{i}}{{\mathfrak{T}}}_{{\rm{i}}},\hspace{2cm}g(k)={g}_{k}^{0}+{{\rm{i}}{g}}_{k}^{1},\end{eqnarray} \tag{ B4 }$$

remembering that ${g}_{k}^{0}={g}_{-k}^{0}$ and ${g}_{k}^{1}=-{g}_{-k}^{1}$ (i.e. the variables are correlated). Our target angle $\phi ={\tan }^{-1}{{\mathfrak{T}}}_{i}/{{\mathfrak{T}}}_{r}$, and so we can calculate

$$\begin{eqnarray}\begin{array}{rcl}\mathrm{Var}(\phi ) & = & \displaystyle \sum _{a,k}{\left[\displaystyle \frac{\partial \phi }{\partial {g}_{k}^{a}}\right]}^{2}\mathrm{Var}[{g}_{k}^{a}]\\ & = & {\left[\displaystyle \frac{1}{{{\mathfrak{T}}}_{r}^{2}+{{\mathfrak{T}}}_{i}^{2}}\right]}^{2}\displaystyle \sum _{a,k}{\left[{{\mathfrak{T}}}_{r}\displaystyle \frac{\partial {{\mathfrak{T}}}_{i}}{\partial {g}_{k}^{a}}-{{\mathfrak{T}}}_{i}\displaystyle \frac{\partial {{\mathfrak{T}}}_{r}}{\partial {g}_{k}^{a}}\right]}^{2}\mathrm{Var}[{g}_{k}^{a}].\end{array}\end{eqnarray} \tag{ B5 }$$

Let us expand out our real and imaginary components of ${\mathfrak{T}}$:

$$\begin{eqnarray}&&{{\mathfrak{T}}}_{r}=\displaystyle \frac{{\displaystyle \sum }_{k=-K}^{K-1}({g}_{k}^{0}{g}_{k+1}^{0}+{g}_{k}^{1}{g}_{k+1}^{1})}{{\displaystyle \sum }_{k=-K}^{K-1}{\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2}},\end{eqnarray} \tag{ B6 }$$

$$\begin{eqnarray}&&{{\mathfrak{T}}}_{i}=\displaystyle \frac{{\displaystyle \sum }_{k=-K}^{K-1}({g}_{k}^{0}{g}_{k+1}^{1}-{g}_{k}^{0}{g}_{k+1}^{1})}{{\displaystyle \sum }_{k=-K}^{K-1}{\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2}}.\end{eqnarray} \tag{ B7 }$$

Then, we can calculate their derivatives as (recalling again that ${g}_{k}^{0}={g}_{-k}^{0}$ and ${g}_{k}^{1}={g}_{-k}^{1}$)

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\mathfrak{T}}}_{r}}{\partial {g}_{k}^{a}}=\displaystyle \frac{2}{1+{\delta }_{k,0}}\left[\displaystyle \frac{(1-{\delta }_{k,K}){g}_{k+1}^{a}+{g}_{k-1}^{a}-2{{\mathfrak{T}}}_{r}{g}_{k}^{a}}{{\displaystyle \sum }_{k=-K}^{k+1}({\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2})}\right],\end{eqnarray} \tag{ B8 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\mathfrak{T}}}_{i}}{\partial {g}_{k}^{a}}=\displaystyle \frac{2{\left(-1\right)}^{a}}{1+{\delta }_{k,0}}\left[\displaystyle \frac{(1-{\delta }_{k,K}){g}_{k+1}^{1-a}-{g}_{k-1}^{1-a}-2{{\mathfrak{T}}}_{i}{g}_{k}^{a}}{{\displaystyle \sum }_{k=-K}^{k+1}({\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2})}\right].\end{eqnarray} \tag{ B9 }$$

Substituting in for g_k^a, we find that everything precisely cancels when $k\ne K$!

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\mathfrak{T}}}_{r}}{\partial {g}_{k}^{0}}=-\displaystyle \frac{\partial {{\mathfrak{T}}}_{i}}{\partial {g}_{k}^{1}}=-2{\delta }_{k,K}\displaystyle \frac{\cos ((K+1)\phi )}{{\displaystyle \sum }_{k=-K}^{k+1}({\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2})},\end{eqnarray} \tag{ B10 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\mathfrak{T}}}_{i}}{\partial {g}_{k}^{0}}=\displaystyle \frac{\partial {{\mathfrak{T}}}_{r}}{\partial {g}_{k}^{1}}=-2{\delta }_{k,K}\displaystyle \frac{\sin ((K+1)\phi )}{{\displaystyle \sum }_{k=-K}^{k+1}({\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2})}.\end{eqnarray} \tag{ B11 }$$

Our variance is then

$$\begin{eqnarray}\begin{array}{rcl}\mathrm{Var}(\phi ) & = & {\left[\displaystyle \frac{2}{\left({{\mathfrak{T}}}_{r}^{2}+{{\mathfrak{T}}}_{i}^{2}){\displaystyle \sum }_{k=-K}^{k+1}({\left({g}_{k}^{0}\right)}^{2}+{\left({g}_{k}^{1}\right)}^{2}\right)}\right]}^{2}\\ & & \times \left\{\mathrm{Var}[{g}_{K}^{0}]{\left(-\cos (\phi )\sin ((K+1)\phi )+\sin (\phi )\cos ((K+1)\phi )\right)}^{2}\right.\\ & & \left.+\mathrm{Var}[{g}_{K}^{1}]{\left(\cos (\phi )\cos ((K+1)\phi )+\sin (\phi )\sin ((K+1)\phi )\right)}^{2}\right\}\\ & = & {\left[\displaystyle \frac{1}{K}\right]}^{2}\left\{\mathrm{Var}[{g}_{K}^{0}]{\sin }^{2}(K\phi )+\mathrm{Var}[{g}_{K}^{1}]{\cos }^{2}(K\phi )\right\}.\end{array}\end{eqnarray} \tag{ B12 }$$

If g_K^a is estimated with N shots, we expect $\mathrm{Var}[{g}_{K}^{0}]=\tfrac{1}{N}$, and

$$\begin{eqnarray}&&\mathrm{Var}(\phi )\propto \displaystyle \frac{1}{{K}^{2}N}.\end{eqnarray} \tag{ B13 }$$

As described in section 3.1.1, for multi-round experiments we weight the least-squares inversion as per equation (27). This weighting adjusts the g_k^a values in equations (B8), (B9) so that $\tfrac{\partial \phi }{\partial {g}_{k}^{A}}$ is no longer zero when $k\lt K$. The sum over k in equation (B5) then lends an extra factor of K to the variance, reducing it to

$$\begin{eqnarray}&&\mathrm{Var}(\phi )\propto \displaystyle \frac{1}{{KN}}.\end{eqnarray} \tag{ B14 }$$

For simplicity, we first consider when the starting state is a simple eigenstate $| {\phi }_{j}\rangle$. After each multi-round experiment we would like to update the probability distribution P(ϕ_j = ϕ), i.e. ${P}_{n}(\phi )=\tfrac{{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| \phi )}{P({\bf{m}})}{P}_{n-1}(\phi )$. We will represent the 2π-periodic probability distribution P_n(ϕ) by a Fourier series with a small number of Fourier coefficients $\#\mathrm{freq}$ which are updated after each experiment, that is, we write

$$\begin{eqnarray}&&P(\phi )={p}_{0}+\displaystyle \sum _{j=1}^{\#\mathrm{freq}-1}\left({p}_{2j-1}\sin (j\phi )+{p}_{2j}\cos (j\phi )\right)\equiv {\boldsymbol{p}}.\end{eqnarray} \tag{ C1 }$$

We thus collect the coefficients as a $\#\mathrm{freq}$-component vector ${\boldsymbol{p}}$. The Fourier representation has the advantage that integration is trivial i.e. ${\int }_{-\pi }^{\pi }P(\phi ){\rm{d}}\phi =2\pi {p}_{0}$ so that the probability distribution is easily normalized. In addition, the current estimate $\tilde{\phi }$ is easy to obtain:

$$\begin{eqnarray}&&\tilde{\phi }={\rm{\arg }}(\langle {{\rm{e}}}^{{\rm{i}}\phi }{\rangle }_{P})={\rm{\arg }}({p}_{2}+{{\rm{i}}{p}}_{1}).\end{eqnarray} \tag{ C2 }$$

Another observation is that the Holevo phase variance is easily obtained from this Fourier representation as

$$\begin{eqnarray}&&\mathrm{Var}(P(\phi ))=\displaystyle \frac{1}{| \langle {{\rm{e}}}^{{\rm{i}}\phi }{\rangle }_{P}{| }^{2}}-1=\displaystyle \frac{1}{{\pi }^{2}({p}_{2}^{2}+{p}_{1}^{2})}-1.\end{eqnarray} \tag{ C3 }$$

Note that this is the Holevo phase variance of the posterior distribution of a single simulation instance. By comparison, in figure 4 we have calculated the same quantity over repeat simulations. However, in general we find the two to be equivalent.

The other advantage of the Fourier representation is that a single-round in an experiment is the application of a sparse matrix on p. One has $P(\phi )\to {P}_{{k}_{r},{\beta }_{r}}({m}_{r}| \phi )P(\phi )={\cos }^{2}({k}_{r}\phi /2+\gamma /2)P(\phi )$, where γ = β_r + m_rπ which is equivalent to

$$\begin{eqnarray}&&{\bf{p}}\to \displaystyle \frac{1}{2}{\bf{p}}+\displaystyle \frac{1}{4}\cos (\gamma ){M}^{0}({k}_{r}){\bf{p}}+\displaystyle \frac{1}{4}\sin (\gamma ){M}^{1}({k}_{r}){\bf{p}}.\end{eqnarray} \tag{ C4 }$$

The coefficients of the update matrices M^0,1(k_r) can be simply calculated using the double angle formulae and employing

$$\begin{eqnarray}&&\begin{array}{l}{\cos }^{2}(k\phi /2+\gamma /2)\cos (j\phi )\\ \quad =\,\displaystyle \frac{1}{2}\cos (j\phi )+\displaystyle \frac{1}{4}\cos (\gamma )\left(\cos ((j+k)\phi )+\cos ((j-k)\phi )\right)\,\\ \quad +\,\displaystyle \frac{1}{4}\sin (\gamma )\left(\sin ((j-k)\phi )-\sin ((j+k)\phi )\right),\end{array}\end{eqnarray} \tag{ C5 }$$

and

$$\begin{eqnarray}&&\begin{array}{l}{\cos }^{2}(k\phi /2+\gamma /2)\sin (j\phi )\\ \quad =\,\displaystyle \frac{1}{2}\sin (j\phi )+\displaystyle \frac{1}{4}\cos (\gamma )\left(\sin ((j+k)\phi )+\sin ((j-k)\phi )\right)\,\\ \quad +\,\displaystyle \frac{1}{4}\sin (\gamma )\left(\cos ((j+k)\phi )-\cos ((j-k)\phi )\right).\end{array}\end{eqnarray} \tag{ C6 }$$

The matrices M^a(n) are then calculated from the above equations. When j > k, we have

$$\begin{eqnarray*}&&\begin{array}{l}{[{M}^{0}(k)]}_{2j+2k,2j}=1,\ \ \ {[{M}^{0}(k)]}_{2j-2k,2j}=1,\\ {[{M}^{0}(k)]}_{2j+2k-\mathrm{1,2}j-1}=1,\ \ \ {[{M}^{0}(k)]}_{2j-2k-\mathrm{1,2}j-1}=1,\\ {[{M}^{1}(k)]}_{2j+2k-\mathrm{1,2}j}=-1,\ \ \ {[{M}^{1}(k)]}_{2j-2k-\mathrm{1,2}j}=1,\\ {[{M}^{1}(k)]}_{2j+2k,2j-1}=1,\ \ \ {[{M}^{1}(k)]}_{2j-2k,2j-1}=-1.\end{array}\end{eqnarray*}$$

When j ≤ k, we have to account for the sign change in $\sin ((j-k)\phi )$:

$$\begin{eqnarray*}&&\begin{array}{l}{[{M}^{0}(k)]}_{j+2k,j}=1,\ \ \ {[{M}^{0}(k)]}_{2k-2j,2j}=1,\\ {[{M}^{0}(k)]}_{2k-2j-\mathrm{1,2}j-1}=-1\\ {[{M}^{0}(k)]}_{2k,0}=-2,\ \ \ {[{M}^{0}(k)]}_{4k-\mathrm{1,2}k-1}=1\\ {[{M}^{1}(k)]}_{2j+2k-\mathrm{1,2}j}=-1,\ \ \ {[{M}^{1}(k)]}_{2k-2j-\mathrm{1,2}j}=-1,\\ {[{M}^{1}(k)]}_{2j+2k,2j-1}=1,\ \ \ {[{M}^{1}(k)]}_{2k-2j,2j-1}=-1,\\ {[{M}^{1}(k)]}_{2k-\mathrm{1,0}}=2,\ \ \ {[{M}^{1}(k)]}_{4k-\mathrm{1,2}k}=1.\end{array}\end{eqnarray*}$$

For a multi-round experiment with R rounds, one thus applies such sparse matrices to the vector p R times. Note that each round with given k_r requires at most k_r more Fourier components, hence an experiment with at most K controlled-U applications adds at most K Fourier components. Thus, when the total number of unitary rotations summed over all experiments ${K}_{\mathrm{tot}}={\sum }_{n}{\sum }_{r}{k}_{r}\gt \#\mathrm{freq}$, our representation of the distribution is no longer accurate. When ${K}_{\mathrm{tot}}\leqslant \#\mathrm{freq}$ on the other hand, it will be accurate.

C.1. Bayesian updating for multi-eigenvalue starting state

In this section we detail the method by which we store the distributions ${P}_{n}^{j}({\phi }_{j})$ and ${P}_{n}^{\mathrm{red}}({\bf{A}})$ of equation (31) and perform the Bayesian update of equation (30). We do so by representing the marginal probabilities ${P}_{n}^{j}({\phi }_{j})$ by a Fourier series with a small number of Fourier coefficients which are updated after each experiment as shown in the previous section. We assume that there are most ${N}_{\mathrm{eig}}$ coefficients A_j > 0 and thus ${N}_{\mathrm{eig}}$ ϕ_j.

From our independence assumption, individual updates of P^j(ϕ_j) may be calculated by integrating out the other unknown variables in equation (30):

$$\begin{eqnarray}&&{P}_{n}^{j}({\phi }_{j})=\int \left(\displaystyle \prod _{l\ne j}{\rm{d}}{\phi }_{l}{P}_{n-1}^{l}({\phi }_{l})\right)\int {\rm{d}}{\bf{A}}\ {P}_{n-1}^{\mathrm{red}}({\bf{A}}){P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}}| {\boldsymbol{\phi }},{\bf{A}}){P}_{n-1}^{j}({\phi }_{j}).\end{eqnarray} \tag{ C7 }$$

Expanding the conditional probability of equation (10) and rewriting leads to the form

$$\begin{eqnarray}&&{P}_{n}^{j}({\phi }_{j})=\displaystyle \frac{1}{{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}})}\left(C+{B}_{j}\displaystyle \prod _{r}{P}_{{k}_{r},{\beta }_{r}}({m}_{r}| {\phi }_{j})\right){P}_{n-1}^{j}({\phi }_{j}),\end{eqnarray} \tag{ C8 }$$

with

$$\begin{eqnarray*}&&C=\displaystyle \sum _{k\ne j}{B}_{k}\int {\rm{d}}{\phi }_{k}{P}_{n-1}^{k}({\phi }_{k})\displaystyle \prod _{r}{P}_{{k}_{r},{\beta }_{r}}({m}_{r}| {\phi }_{k}),\end{eqnarray*}$$

and ${B}_{j}=\int {\rm{d}}{\bf{A}}\ {P}_{n-1}^{\mathrm{red}}({\bf{A}}){A}_{j}$. Here we have used that $\int {\rm{d}}{\phi }_{l}{P}_{n-1}^{l}({\phi }_{l})=1$. One can concisely write B_j as the components of a vector ${\bf{B}}$. Computing equation (30) then involves creating an 'update' distribution for each ϕ_j, calculating the integral of each distribution, and then forming the new distribution from a weighted sum from the 'update' distributions.

Calculating the distribution ${P}_{n}^{\mathrm{red}}({\bf{A}})$ is complicated slightly by the restriction that ${\sum }_{j}{A}_{j}=1,{A}_{j}\geqslant 0$, meaning that we cannot assume the distribution of individual A_j terms is uncorrelated. The marginal probability distribution equals

$$\begin{eqnarray}&&{P}_{n}^{{\rm{red}}}({\bf{A}})=\displaystyle \frac{{P}_{n-1}^{{\rm{red}}}({\bf{A}})}{{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}})}\displaystyle \sum _{j}{A}_{j}\int {\rm{d}}{\phi }_{j}{P}_{n-1}^{j}({\phi }_{j})\displaystyle \prod _{r}{P}_{{k}_{r},{\beta }_{r}}({m}_{r}| {\phi }_{j}).\end{eqnarray} \tag{ C9 }$$

or

$$\begin{eqnarray}&&{P}_{n}^{\mathrm{red}}({\bf{A}})=\displaystyle \frac{{P}_{n-1}^{\mathrm{red}}({\bf{A}})}{{P}_{{\bf{k}},{\boldsymbol{\beta }}}({\bf{m}})}{\bf{A}}\cdot {{\bf{q}}}_{n-1},\end{eqnarray} \tag{ C10 }$$

where the jth component ${({q}_{n-1})}_{j}$ is the integral

$$\begin{eqnarray}&&{\left({q}_{n-1}\right)}_{j}=\int {\rm{d}}{\phi }_{j}{P}_{n-1}^{j}({\phi }_{j})\displaystyle \prod _{r}{P}_{{k}_{r},{\beta }_{r}}({m}_{r}| {\phi }_{j}).\end{eqnarray} \tag{ C11 }$$

As A only enters our estimation through the vector ${\bf{B}}=({B}_{0},\,\ldots ,\,{B}_{{N}_{\mathrm{eig}}})$, we only need approximate this value. Assuming we know the marginal probabilities P_n(ϕ_j) for all experiments n = 1, ..., N, we can estimate B after all experiments by the maximum likelihood value ${{\bf{A}}}^{(\max )}$

$$\begin{eqnarray*}\begin{array}{rcl}{{\bf{A}}}_{N}^{(\max )} & = & \mathop{\arg \max }\limits_{{\bf{A}}}f({\bf{A}})\\ f({\bf{A}}) & = & \mathrm{log}\left({P}_{\mathrm{prior}}({\bf{A}})\displaystyle \prod _{n=1}^{N}{\bf{A}}\cdot {{\bf{q}}}_{n}\right)\\ & = & \mathrm{log}({P}_{\mathrm{prior}}({\bf{A}}))+\displaystyle \sum _{n=1}^{N}\mathrm{log}({\bf{A}}\cdot {{\bf{q}}}_{n}).\end{array}\end{eqnarray*}$$

Evaluating this equation for up N = 1000 experiments, taking $\#\mathrm{freq}=10\,000$ frequency components of ${N}_{\mathrm{eig}}=2$ eigenvalues takes less than a second on a laptop using a method such as sequential least-squares programming [41]. However, beyond this it becomes fairly computationally intensive. Thus, after N > 100 experiments have been performed, we switch to a local optimization method. We determine the optimal B_n after n experiments from its prior value ${{\bf{B}}}_{n-1}$ via a single step of an approximate Newton's method, that is, we take

$$\begin{eqnarray*}&&{{\bf{B}}}_{n}={{\bf{B}}}_{n-1}-{\rm{\Pi }}[{{\bf{H}}}^{-1}(f({{\bf{B}}}_{n-1}))\ (\vec{{\rm{\nabla }}}f)({{\bf{B}}}_{n-1})],\end{eqnarray*}$$

where $\vec{{\rm{\nabla }}}f({\bf{A}})$ is the first derivative of f at A and H is the Hessian matrix of f, i.e. ${H}_{{ij}}={\partial }_{{A}_{i}}{\partial }_{{A}_{j}}f({\bf{A}})$. Here Π[A] is the projector onto the plane ${\sum }_{j=0}^{{N}_{\mathrm{eig}}}{A}_{j}=1$ so that the update preserves the normalization. We have

$$\begin{eqnarray*}&&{\partial }_{{A}_{i}}f({\bf{A}})=\displaystyle \frac{{\partial }_{{A}_{i}}{P}_{\mathrm{prior}}({\bf{A}})}{{P}_{\mathrm{prior}}({\bf{A}})}+\displaystyle \sum _{n=1}^{N}\displaystyle \frac{{\left({q}_{n}\right)}_{i}}{{\bf{A}}\cdot {{\bf{q}}}_{n}}\end{eqnarray*}$$

We approximate the second term for each step as coming from only from the added term, i.e.

$$\begin{eqnarray}&&\vec{{\rm{\nabla }}}f({{\bf{B}}}_{n-1})\approx \displaystyle \frac{{{\bf{q}}}_{n}}{{{\bf{B}}}_{n-1}\cdot {{\bf{q}}}_{n}}.\end{eqnarray} \tag{ C12 }$$

The Hessian equals

$$\begin{eqnarray}&&{H}_{{ij}}(f({\bf{A}}))=-\displaystyle \sum _{n=1}^{N}\displaystyle \frac{{\left({q}_{n}\right)}_{i}{\left({q}_{n}\right)}_{j}}{{\left({\bf{A}}\cdot {{\bf{q}}}_{n}\right)}^{2}},\end{eqnarray} \tag{ C13 }$$

but we approximate this at the nth step

$$\begin{eqnarray}&&{H}_{{ij}}^{(n)}(f({{\bf{B}}}_{n-1}))\approx {H}_{{ij}}^{(n-1)}-\displaystyle \frac{{\left({q}_{n}\right)}_{i}{\left({q}_{n}\right)}_{j}}{{\left({{\bf{B}}}_{n}\cdot {{\bf{q}}}_{n}\right)}^{2}}.\end{eqnarray} \tag{ C14 }$$

This approximation allows H to be updated without summing over each experiment.

With the above implemented, we observe that our estimator can process data from N = 10 000 experiments to estimate ${N}_{\mathrm{eig}}=2$ eigenvalues with N = 20 000 Fourier components within approximately two minutes on a laptop. Unfortunately, this method scales as N², as the number of frequencies required for accurate estimation grows as the total number of unitaries applied.

As the mean, variance and integration calculations only require the first few frequencies of the distribution, it may be possible to reduce this cost by finding approximation techniques for higher frequency components.

In this section we present an expansion of figure 6, namely figure D1, by drawing the spurious eigenvalues ϕ_j from a range closer to the target eigenvalue ϕ₀. This negates the drop in estimation error observed in figure 6 that was caused by the majority of eigenvalues lying in region (c) of figure 5. We observe that for certain gaps δ, multiple eigenvalues confined to a thin region $[\delta ,{\phi }_{\max }]$ can have a worse effect on our ability to estimate ϕ₀ than that of a single eigenvalue at δ. However, this loss in accuracy does not get critically worse with the addition of more eigenvalues. Neither is it worse than the worst-possible estimation with two eigenvalues.

Zoom In Zoom Out Reset image size

In this appendix we give details of the method for the realistic noisy circuit simulation of section 5.2. Our density-matrix simulator is fairly limited in terms of qubit number, and so we opt to simulate H₄ in the STO-3G basis. This molecule has 8 spin orbitals and thus requires 9 qubits for the QPE simulation (with the additional qubit being the ancilla). We choose 10 rectangular molecular geometries for the H₄ system, parametrized by a horizontal distance d_x and a vertical distance d_y (i.e. the four H atoms are in the positions $(\pm {d}_{x}/2,\pm {d}_{y}/2,0)$). We calculate the Hartree–Fock and full-CI solutions to the ground state using the psi4 package [38] with the openfermion interface [9]. This allows to calculate the true ground state energy E₀ for each geometry, and the overlap A₀ between the ground state and the Hartree–Fock state, which we choose as our starting state $| {\rm{\Psi }}\rangle$. Due to symmetry and particle number conservation, $| {\rm{\Psi }}\rangle$ has non-zero overlap with only 8 eigenstates of the full-CI solution, separated from the ground state by a minimum gap δ. (When d_x = d_y, the true ground state of H₄ is actually orthogonal to the Hartree–Fock state, and so we do not include any such geometries in our calculation.) The full error in our calculation of the energy (at a fixed geometry) is then a combination of three separate contributions: basis set error (i.e. from the choice of orbitals), Trotter error, and the estimator error studied in this work (which includes error from experimental noise). The Trotter error _Trotter is reasonably large due to our use of only the first-order Suzuki-Trotter approximation $U={\prod }_{i}{{\rm{e}}}^{-{{\rm{i}}{H}}_{i}t}\approx {{\rm{e}}}^{-{\rm{i}}{\boldsymbol{ \mathcal H }}t}$. Higher-order Suzuki-Trotter expansions require longer quantum circuits, which in turn increase the estimator error from experimental noise. Balancing these two competing sources of error is key to obtaining accurate calculations and a clear target for future study. In table E1, we list some parameters of interest for each studied geometry. We normalize the gap and the Trotter error by the Frobenius norm $\parallel {\boldsymbol{ \mathcal H }}{\parallel }_{F}=\sqrt{\mathrm{Trace}[{{\boldsymbol{ \mathcal H }}}^{\dagger }{\boldsymbol{ \mathcal H }}]/{2}^{{n}_{\mathrm{sys}}}}$, as we chose an evolution time $t=1/\parallel {\boldsymbol{ \mathcal H }}{\parallel }_{F}$, making this the relevant scale for comparison with scaling laws and errors calculated in the text.

Table E1.  Parameters of the H₄ geometries used in the text. Terms are described in appendix E. $| | {\boldsymbol{ \mathcal H }}| {| }_{F}=\sqrt{\mathrm{Trace}[{{\boldsymbol{ \mathcal H }}}^{\dagger }{\boldsymbol{ \mathcal H }}]/{2}^{{n}_{\mathrm{sys}}}}$.

dx [Å]	dy [Å]	E0	A0	δ/$\parallel {\boldsymbol{ \mathcal H }}{\parallel }_{F}$	${\epsilon }_{\mathrm{Trotter}}/\parallel {\boldsymbol{ \mathcal H }}{\parallel }_{F}$
0.4	0.5	−0.26	0.98	0.09	3.7 × 10−4
0.6	0.7	−1.46	0.94	0.17	3.1 × 10−3
0.8	0.9	−1.84	0.88	0.24	0.016
1.0	1.1	−1.96	0.80	0.23	0.017
1.2	1.3	−1.98	0.71	0.18	0.013
1.6	1.7	−1.94	0.55	0.09	6.0 × 10−3
0.2	1.8	0.32	0.996	0.67	2.0 × 10−4
0.4	1.6	−1.80	0.993	1.14	2.6 × 10−3
0.6	1.4	−2.15	0.98	1.27	0.014
0.8	1.2	−2.09	0.96	0.73	0.021

E.1. Error model and error parameters

Throughout this work we simulate circuits using an error model of superconducting qubits first introduced in [37]. This captures a range of different error channels with parameters either observed in experimental data or estimated via theory calculations. All error channels used are listed in table E2, and we will now describe them in further detail.

Table E2.  Standard parameters of error models used in density matrix simulation. Table adapted from [37] with all parameters taken from therein (with the exception of the 1/f flux noise, which is made incoherent as described in text).

Parameter	Symbol	Standard value	Scaling
Qubit relaxation time	T1	30 μs	λ
Qubit dephasing time	T2	30 μs	λ
Single-qubit gate time	Tsq	20 ns	1
Two-qubit gate time	T2q	40 ns	1
In-axis rotation error	paxis	10−4	λ−1
In-plane rotation error	pplane	5 × 10−4	λ−1
Incoherent flux noise	A	${(1\mu {{\rm{\Phi }}}_{0})}^{2}$	λ−1
Measurement time	Tmeas	300 ns	1
Depletion time	Tdep	300 ns	1
Readout infidelity	RO	5 × 10−3	λ−1
Measurement induced decay	${p}_{{\rm{d}},{\rm{i}}},{p}_{{\rm{d}},{\rm{f}}}$	0.005, 0.001 5	λ−1

Transmon qubits are dominated primarily by decoherence, which is captured via T₁ and T₂ channels [4]. Typical T₁ and T₂ times in state-of-the-art devices are approximately 10−100 μs. As other error parameters are derived from experimental results on a device with T₁ = T₂ ≈ 30 μs, we take these as a base set of parameters [42, 43]. Single-qubit gates in transmon qubits incur slight additional dephasing due to inaccuracies or fluctuations in microwave pulses. We assume such dephasing is Markovian, in which case it corresponds to a shrinking of the Bloch sphere along the axis of rotation by a value $1-{p}_{\mathrm{axis}}$, and into the perpendicular plane by a value $1-{p}_{\mathrm{plane}}$. We take typical values for these parameters as ${p}_{\mathrm{axis}}={10}^{-4}$, ${p}_{\mathrm{plane}}=5\times {10}^{-4}$ [37].

Two-qubit gates in transmon qubits incur dephasing due to 1/f flux noise. Assuming that the phase in an ideal C-phase gate $G=\mathrm{diag}(1,1,1,{{\rm{e}}}^{{\rm{i}}\phi }))$ is controlled by adjusting the time of application, this suggests a model for the applied gate which is

$$\begin{eqnarray}G({\delta }_{{\rm{flux}}})=\left(\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & {{\rm{e}}}^{{\rm{i}}{\delta }_{{\rm{flux}}}\phi } & 0\\ 0 & 0 & 0 & {{\rm{e}}}^{{\rm{i}}(1+{\delta }_{{\rm{flux}}}/2)\phi }\end{array}\right),\end{eqnarray} \tag{ E1 }$$

where δ_flux is drawn from a normal distribution around 0 with standard deviation σ_flux. One can estimate σ_flux ≈ 0.01 rad for a typical gate length of 40 ns [37]. The noise is in general non-Markovian, as δ_flux fluctuates on longer timescale than a single gate. However, to make the simulation tractable, we approximate it as Markovian. The Pauli transfer matrix of this averaged channel [44] reads

$$\begin{eqnarray}&&{\rm{\Lambda }}[G]=\int {\rm{d}}{\delta }_{{\rm{flux}}}P({\delta }_{{\rm{flux}}}){\rm{\Lambda }}[G({\delta }_{{\rm{flux}}})],\end{eqnarray} \tag{ E2 }$$

where the Pauli transfer matrix of a channel G is given by ${\rm{\Lambda }}{[G]}_{i,j}=\mathrm{Tr}[{\sigma }_{i}G{\sigma }_{j}]$.

During qubit readout, we assume that the qubit is completely dephased and projected into the computational basis. We then allow for a T_meas = 300 ns period of excitation and de-excitation (including that from T₁-decay), during which the qubit state is copied onto a classical bit. This copying is also assumed to be imperfect, with a probability _RO of returning the wrong result. The qubit then has an additional T_dep = 300 ns waiting period before it may participate in gates again (to allow resonator depletion [42]), over which additional excitation and de-excitation may occur. Though simple, this description is an accurate model of experimental results. Typically experiments do not observe measurement-induced excitation to the $| 1\rangle$ state, but do observe measurement-induced decay [37]. Typical values of such decay are 0.005 prior to the copy procedure, and 0.015 after.

Though reasonably accurate, this error model does fail to capture some details of real experimental systems. In particular, we do not include leakage to the $| 2\rangle$ state, which is a dominant source of two-qubit gate error. Furthermore, we have not included cross-talk between qubits.

To study the effect of changing noise levels while staying as true as possible to our physically-motivated model, we scale our noise parameters by a dimensionless parameter λ such that the contribution from each error channel to the simulation remains constant. In table E2 we show the power of λ that each error term is multiplied by during this scaling. We report T_err := T₁ = T₂ in the main text instead of λ to make connection to parameters regularly reported in experimental works.