Abstract
The present article reports a comprehensive study on structural, elastic, mechanical, acoustical, electronic and thermodynamic properties of XPdF3 (X = Rb, Tl). This study has been carried out using Wien2k computational code written in Fortran language and based on density functional theory. The obtained results explored the ground state stability of these compounds in non magnetic phase. The calculated structural properties including lattice constant, bulk modulus, ground state energy, energy of formation were compared with available literature. In addition, from elastic constants, bulk, shear and elastic moduli, Poisson's ratios and anisotropy factors were calculated. Furthermore, from criteria of Pugh's ratio and Cauchy pressure, the materials were found as ductile. The sound velocities in TlPdF3 were examined as lower than RbPdF3 because of comparatively heavier mass of Tl than Rb atom. The obtained electronic properties give the indications of inclusion of these compounds in category of metallic perovskites. Moreover, the thermodynamic parameters like thermal expansion, heat capacity, Debye temperature and Grüneisen parameter were computed using Debye model.
Export citation and abstract BibTeX RIS
1. Introduction
It is always beneficial to know about the physical properties of a material for its possible applications in advance technology. Among these materials, perovskite structured compounds are famous for their extensive use in different fields of science and technology, as, they have enormous physical properties [1–4]. Perovskite term is used when introducing a broad group of materials having crystal structure as like mineral CaTiO3. Therefore, perovskites are generally formulated as ABM3, where A and B stands for cations from alkali and transition metals respectively, having different sizes in which A-site cation is more electropositive and bigger than B-site cation, and M atom represents anion commonly occupied by oxide ion O2− or halides ions (Cl−, Br−, F−, I−) making two major classes, oxide perovskites and halide perovskites respectively [5, 6]. Ideally, perovskites crystallizes in cubic forms in which A cation is 9–12 fold coordinated by M ions while B cation is 6 Fold coordinated by M ions. The perovskite structure is fairly simple but still a variety numbers of structures are possible among them due to the fact that A and B cations can virtually hold any monovalent and divalent element respectively from the periodic table [7]. The structural diversity and stability of perovskites can be deduced from tolerance factor  Where, RA, RB and RM represents the ionic radii of A, B and M respectively. For cubic halide perovskites (M = Cl, Fl, Br, I) the value of t ranges from 0.81 to 1.11 [8].
Where, RA, RB and RM represents the ionic radii of A, B and M respectively. For cubic halide perovskites (M = Cl, Fl, Br, I) the value of t ranges from 0.81 to 1.11 [8].
In last decades, halide perovskites have drawn significant interest from researchers in the fields of material science, as well as in physics and chemistry due to their tunable and fascinating physical properties such as electric, ferroelectric, piezoelectric, magnetic, thermoelectric, spin dependent transport, two-dimensional electronic conductivity [9, 10], optical, catalytic, and magneto-resistive [11, 12]. On the basis of crystal structure diversity, variety of elements involved and the extent of above mentioned physical properties, halide perovskites have efficient and useful functionalities as solar cell absorbers [13], topological insulators [14], and high efficient solid-state solar cells.
Till now enormous halide perovskites are being investigated both experimentally and theoretically in order to find their structural, elastic, electronic, optical, transport and thermodynamic properties for their possible and more efficient device based use [15–25]. But unfortunately, complete physical properties of XPdF3 (X = Rb, Tl) have to be investigated. According to best of our knowledge, these compounds were examined only for their structural properties [26–30]. Therefore, a detail study about their physical properties for technological applications is need of present era. This article explores possible structural, elastic, mechanical, acoustical, electronic and thermodynamic properties of XPdF3 (X = Rb, Tl) using full potential linearized augmented plane wave method. This study will cover the void in halide perovskite family and will motivate experimenters for further analysis about these important compounds.
2. Method of calculations
Full potential-linearized augmented plane wave (FP-LAPW) scheme [31, 32] within density functional theory (DFT) [23] executed in Wein2k code [33] was utilized in present research work. DFT is a theoretical techniques used in physics and chemistry to solve Kohn–Sham equation (equation (1)) [34] in order to find the physical properties of materials.

Where,  and
and  represents kinetic energy operator and Kohn–Sham orbital wave function respectively while
represents kinetic energy operator and Kohn–Sham orbital wave function respectively while  symbolizes effective potential and is given by:
symbolizes effective potential and is given by:
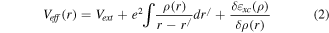
Where,  is interaction potential between electrons and nuclei,
is interaction potential between electrons and nuclei,  is measure of interaction between electrons called Hartree potential while
is measure of interaction between electrons called Hartree potential while  is exchange correlation potential (VEx). For precise first principle calculations, VEx is approximated. In present calculations, PBE-GGA (Perdew-Burke-Ernzehof generalized gradient approximation) [35] was used for VEx.
is exchange correlation potential (VEx). For precise first principle calculations, VEx is approximated. In present calculations, PBE-GGA (Perdew-Burke-Ernzehof generalized gradient approximation) [35] was used for VEx.
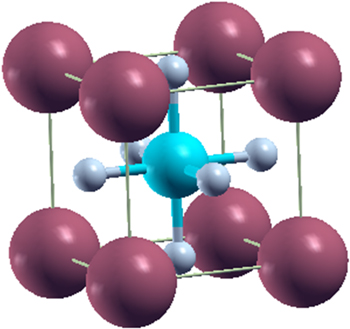
Where, the FP-LAPW method considers the unit cell in two portions (1) non overlapping Muffin Tin spheres and (2) interstitial region. In present work, the radii of Muffin Tin spheres for X, Pd and F (in XPdF3, shown in figure 1) were selected as 2.5, 2.1 and 1.9 a.u, respectively. While, wave function in these spheres, was expanded up to lmax = 10. In interstitial region, the wave functions were expanded in term of plane waves with a cut-off condition of RMTKmax = 7 (RMT represents the small Muffin Tin radius while the Kmax is the size of the largest plane wave reciprocal lattice vector (k)). Further, to ensure the convergence, a dense mesh of 1000 K points was used for integration of Brillion zone.
Figure 1. Crystal structure of XPdF3 (X = Rb, Tl), Corner atoms represent X, body center atom is Pd and face centre atoms are F.
Download figure:
Standard image High-resolution image3. Results and discussion
3.1. Structural properties
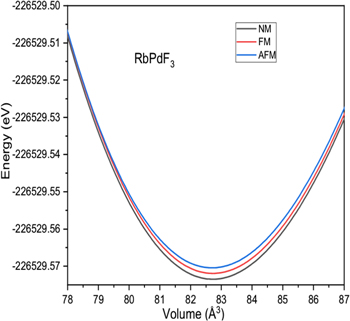
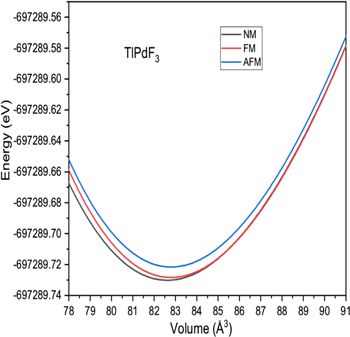
The previous studies [36–42] on halide perovskites reveal the accuracy of GGA for calculations of structural parameters in comparison to other exchange correlation potentials. Therefore, we got motivation for calculation of lattice constant (αo), bulk modulus (B), rate of change of bulk modulus with respect to pressure (B/) and ground state energy (Eo) for XPdF3 (X = Rb, Tl) using PBE-GGA exchange potential. First, the ground state stability of these compounds was tested among non magnetic (NM), ferromagnetic (FM) and anti ferromagnetic (AFM) phases. The resulted ground state energy was found to be less in NM phase. Hence our calculations predict that these compounds are most stable in NM phase in ground state as shown in figures 2 and 3. Therefore, we calculated the structure parameters αo, B, B/ and Eo only in NM phase by art of fitting variables using Birch-Murnaghan equation (equation (3)) [43]. Where, using data of minimization of energy process, energies versus volume was re-plotted with help of equation (3). The constants Vo (αo × αo × αo), B, B/ and Eo were set to fit the re-plotted curves with those in figures 2 and 3. These constants are the obtained structural parameters.
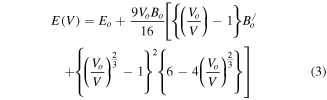
Figure 2. Volume optimization against energy in Non magnetic, ferromagnetic and anti ferromagnetic phases for RbPdF3.
Download figure:
Standard image High-resolution imageFigure 3. Volume optimization against energy in Non magnetic, ferromagnetic and anti ferromagnetic phases for TlPdF3.
Download figure:
Standard image High-resolution imageThe calculated values are repotted in table 1. The available results of experimental [26, 27] and theoretical [28–30] studies on XPdF3 (X = Rb, Tl) are also given in the table for comparison. These confirm the reliability of our present results. Further, the hardness of TlPdF3 is larger than RbPdF3 because of comparatively high bulk modulus. Also the lattice constant of TlPdF3 is greater than RbPdF3 because of grater size of Tl atom than Rb atom.
Table 1. Calculated lattice constant αo, bulk modulus B, bulk modulus pressure derivative B/ and ground state energy Eo for RbPdF3 and TlPdF3 along with available results in literature.
| Compound | Configuration | αo (Å) | B (GPa) | B/ | Eo (Ry) |
|---|---|---|---|---|---|
| RbPdF3 | Present | 4.3586 | 67.72 | 5 | −16 656.586 271 |
| Experimental | 4.2941 [18] | — | |||
| 4.29 [17] | |||||
| Theoretical | 4. 254 [19] | ||||
| 4.290 [20] | |||||
| 4.127 [21] | |||||
| TlPdF3 | Present | 4.3606 | 69.33 | 5 | −51 271.303 668 |
| Experimental | 4.30 [17] | ||||
| Theoretical | 4.247 [19] | ||||
| 4.280 [20] | |||||
| 4.108 [21] |
3.2. Elastic properties
Elastic constants Cij (C11, C12, C44) play significant role in deducing the mechanical behavior of a cubic material. These provide vital information about mechanical stability, ductility or brittleness, nature of binding interactions. These constants also provide enough stuff for calculations of thermodynamic parameters such as melting temperature, Debye temperature [44] etc. In present study Cij were calculated from the relation of strain as a function of unit cell volume using Charpin scheme [45] as employed in Wien2k code. In theoretical calculations, the cubic symmetry of a material in homogeneous expansion can be retained by convergence of elastic constants. Therefore, C11, C12 and C44 were calculated with respect to increasing k points. All three elastic constants (listed in table 2) were converged at 1000 k points. Due to lack of experimental data, our reported elastic constants can be used as reference in future studies about XPdF3 (X = Rb, Tl). However, we confirm the stability of these compounds in cubic phase from following condition [46, 47].
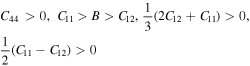
Table 2. Calculated elastic constants C11, C12, C44, bulk (B), Shear (G) and their Voigt (BV, GV), Reuss (BR, GR) bound, and Elastic (E) modules, Poisson's ratio (υ), B/G, Cauchy pressure (C12-C44) and anisotropy factor for RbPdF3 and TlPdF3.
| Parameter | RbPdF3 | TlPdF3 |
|---|---|---|
| C11 (GPa) | 132.99 | 77.70 |
| C12 (GPa) | 33.08 | 65.96 |
| C44 (GPa) | 6.89 | 18.98 |
| BV = BR = B (GPa) | 66.38 | 69.87 |
| GR (GPa) | 10.52 | 10.02 |
| GV (GPa) | 24.12 | 13.74 |
| G (GPa) | 17.32 | 11.88 |
| E (GPa) | 47.79 | 33.73 |
| υ | 0.379 | 0.419 |
| B/G | 3.83 | 5.88 |
| C12-C44 (GPa) | 26.19 | 46.98 |
| A | 0.138 | 3.23 |
3.3. Mechanical properties
Various materials are subjected to loads or forces, when they are in services. In such situations it is essential to know the properties of the material. So, that one may design a structure from those materials which may bear the estimated loads without any deformation and fracture. The mechanical performance of a material replicates the connection between its response and deformation to an applied force or load. Key mechanical design properties are strength, hardness, stiffness, toughness and ductility [48]. These can be tested from calculated results of shear modulus (G), young modulus (E), Poisson's ratio (υ), B/G, and Cauchy pressure (C12–C44) (table 2). These were calculated using by help converged values of elastic constants using below relations [49, 50].
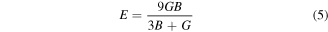
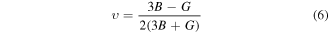
Here, G and B were calculated from average of Voigt and Reuss bounds of share (Gv and GR) and bulk (BV and BR) moduli [51].
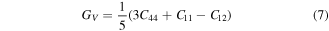
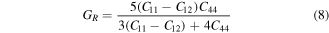
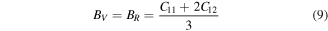
To characterize the stiffness of a material, the measurement of bulk's modulus (B) is required. The material will be stiffer if value of B is higher [52]. In present calculations, B results reveal (table 2) the higher stiffness of TlPdF3 than RbPdF3. Furthermore, the bonding between constituent atoms of a hard material has covalent nature which can be indicated by higher value of shear modulus [53]. The young modulus (E) determines the degree of resistance of a material to plastic deformation [48]. The present calculations explore RbPdF3 as higher resistive to plastic deformation than TlPdF3. The Poisson's ratio (ratio between transverse and longitudinal strains) is another important mechanical parameter which signifies the stability of a compound to shear stress and is indicator of nature of bonding forces. Its possible values are in range of 0 < ʋ < 0.5 [54]. Larger value of ʋ specifies high plasticity of material. Therefore, TlPdF3 has high plasticity in comparison of RbPdF3. Moreover, the bonding forces between both the studied compounds are central type, as calculated ʋ is in allowed range (ʋ ≥ 0.25) of such forces.
The ductile or brittle nature can be recognized by Pugh's ratio (B/G) and Cauchy pressure (C12–C44). According to ductility conditions [55], Pugh's ratio is greater than 1.75 and Cauchy pressure is positive both TlPdF3 and RbPdF3. Therefore, these perovskites are ductile in nature. However, the ductility of TlPdF3 is large in comparison of RbPdF3 because of larger value Pugh's ratio and Cauchy pressure. The complete understanding of the ductile nature of a material is essential for at least two reasons. First, it gives information to a structure designer about the limit of plastic deformation prior to fracture. Second, it indicates the limit of permissible deformation at stage of fabrication process. We occasionally give preference to the materials of high ductility as they may experience local deformation exclusive of fracture.
The elastic anisotropy (A) is an imperative parameter used for measurement of the degree of anisotropy in materials; in addition, it has an important usage in engineering sciences to examine the possible micro cracks in materials [56].
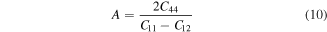
For a perfect isotropic material, A takes the value of unity and the difference from unity quantifies the extent of elastic anisotropy [56]. It is apparent from table 2 that A for both the materials deviates from unity; therefore, they have mechanical anisotropic behavior. Furthermore, TlPdF3 displays more anisotropy than RbPdF3 because it's 'A' finds relatively high deviation from unity.
Melting temperature (TM) is a material's specific defined temperature above which the material changes from solid to liquid state. It can be computed in Kelvin by below empirical formula [57].
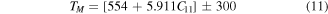
The obtained TM through equation (9) for RbPdF3 [1330.10  ] is greater than TlPdF3 [1013.28
] is greater than TlPdF3 [1013.28  ]. Our calculated values are closer to other reported values of TM for other transitional atom containing fluoride perovskites [19, 42, 48, 58].
]. Our calculated values are closer to other reported values of TM for other transitional atom containing fluoride perovskites [19, 42, 48, 58].
3.4. Acoustical properties
The elastic wave velocities in a material can be calculated from elastic constants. Generally, elastic waves are divided in two modes, longitudinal wave vL having parallel polarization to the direction of transmission and two shear waves vT1 and vT2 with perpendicular polarization to direction of propagation. The computed velocities of elastic waves for XPdF3 (X = Rb, Tl) in [100], [110] and [111] directions (using equations (12), (13) [59, 60]) are given in table 3.
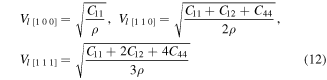
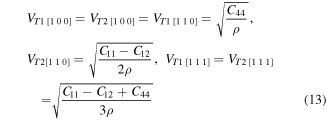
Table 3. Calculated density ρ (g cm−3) and velocities (in m s−1) of elastic waves in [1 0 0], [1 1 0] and [1 1 1] directions for RbPdF3 and TlPdF3.
| Compound | ρ |
![${V}_{l\left[100\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn10.gif)
|
![${V}_{T1\left[100\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn11.gif)
|
![${V}_{T2\left[100\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn12.gif)
|
![${V}_{l\left[110\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn13.gif)
|
![${V}_{T1\left[110\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn14.gif)
|
![${V}_{T2\left[110\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn15.gif)
|
![${V}_{l\left[111\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn16.gif)
|
![${V}_{T1\left[111\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn17.gif)
|
![${V}_{T2\left[111\right]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn18.gif)
|
|---|---|---|---|---|---|---|---|---|---|---|
| RbPdF3 | 3.85 | 5877 | 1338 | 1338 | 4739 | 1338 | 3602 | 4430 | 3041 | 3041 |
| TlPdF3 | 7.36 | 3249 | 1605 | 1605 | 3323 | 1605 | 893 | 3596 | 1179 | 1179 |
From the table it is clear that longitudinal elastic waves are greatest velocity in [100] direction and the shear elastic waves have lowest speed in [110] direction for all the two compounds. These two perovskites have fairly similar acoustic behavior. However, due to relatively heavier mass of Tl in comparison of Rb, TlPdF3 has lower sound velocities than RbPdF3.
3.5. Electronic properties
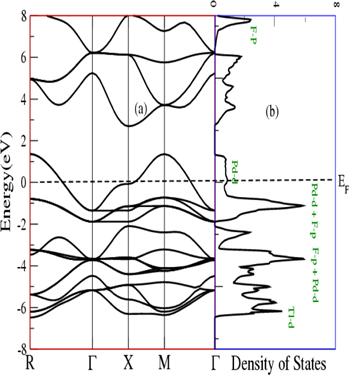
Equilibrium lattice constants were utilized for calculation of electronic properties. These properties are associated with band structure and density of states (DOS) and are used for predicting of the electronic nature of a material. The calculated band structures with corresponding DOS are given in figures 4 and 5. Since, band structures of the spins up and down channel are replica of each other. Therefore, here we are presenting electronic properties only in spin up channel. It can be seen from figures that for both compounds, the valence band states cross the Fermi level and reaches at 1.3 eV in the conduction band. Therefore, these compounds are metallic. From DOS plots in panel b of figures, it can be deduced that the valence band extends from −7 eV to 1.3 eV, and is mainly populated by d and p states of Pd and F atoms respectively with minor contribution of d states X atom in lower part. The conduction band is majorly occupied by p states of F with minor collaboration of other all states of constituent atoms, and extends from 3 eV to 8 eV.
Figure 4. (a) Band structure (b) Density of states plots for RbPdF3.
Download figure:
Standard image High-resolution imageFigure 5. (a) Band structure (b) Density of states plots for TlPdF3.
Download figure:
Standard image High-resolution image3.6. Enthalpy of formation
For further verification of thermodynamic stability of XPdF3 (X = Rb, Tl) in cubic phase, we have calculated enthalpy of formation (ΔH) by taking difference between total ground state energy of these compounds and their constituent atoms by following equation [16]
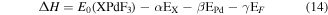
Here,  is the total ground state energy of
is the total ground state energy of  and
and 

 are the energies of distinct atoms in their respective lattice, per unit cell. The numbers of atoms X (Rb or Tl), Pd and F per unit cell are indicated by letters α, β and γ respectively. The calculated values of ΔH for RbPdF3 and TlPdF3 are −1.291 274 Ry and −1.1444 Ry, respectively. The negative sign of
are the energies of distinct atoms in their respective lattice, per unit cell. The numbers of atoms X (Rb or Tl), Pd and F per unit cell are indicated by letters α, β and γ respectively. The calculated values of ΔH for RbPdF3 and TlPdF3 are −1.291 274 Ry and −1.1444 Ry, respectively. The negative sign of  signify the formation reactions of investigated compounds as exothermic. This assures the stability of the compounds in cubic phase.
signify the formation reactions of investigated compounds as exothermic. This assures the stability of the compounds in cubic phase.
3.7. Thermodynamic properties
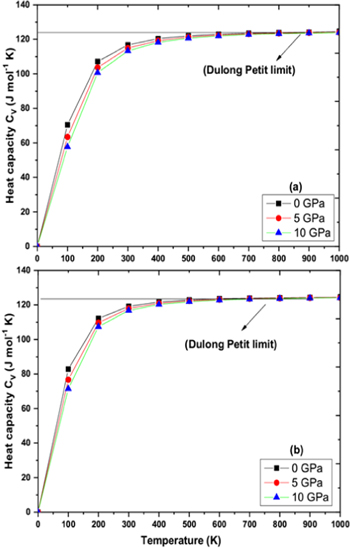
By applying Quasi-harmonic Debye approximation [61], RbPdF3 and TlPdF3 were investigated for thermodynamic properties. The variation of cell volume, bulks modulus, Debye temperature (θD), thermal expansion (α), heat capacity (Cv) and Grüneisen parameter (γ) with respect to pressure and temperature have been plotted and discussed. The temperature and pressure were taken in range of 0–1000 K (with gap of 100 K) and 0–10 GPa (with gap 5 GPa) respectively. Figures 6(a), (b) shows the pressure and temperature dependence of cell volume respectively for RbPdF3 and TlPdF3. From these figures, it is clearly observed that unit cell volume increases with rise in temperature while it decreases with increasing pressure. This is due to the compression and relaxation due to change of pressure and temperature respectively. The variation in volume with changing temperature and pressure is a general trend in solids. Figures 7(a), (b) presents the variation in bulk modulus B while changing temperature and pressure for RbPdF3 and TlPdF3. From these figures, we observe a decrease in the value of B with respect to temperature whereas B is found to increase with pressure. The computed B values are 66.04 GPa and 67.43 GPa respectively for RbPdF3 and TlPdF3 at 0 GPa pressure and 0 K temperature. These values are in accordance to the values obtained from Birch-Murnaghan equation of state and elastic constants. However, it is also clear from thermodynamic calculations that the nature of stiffer resistance of TlPdF3 is little greater than RbPdF3. Figures 8(a), (b) presents the specific heat (CV) as function of pressure and temperature. Under various pressures and temperatures, the nature of CV diagram for both the compounds is nearly similar. CV starts to rise quickly within 0 K to 200 K (usually low temperature range), after 200 K a lethargic rise in the value of CV is observed up to 600 K, and beyond that it becomes constant. Rapid increase in CV within 0 K to 200 K temperature pursues renowned Debye model ![$\left[{C}_{V}(T)/{T}^{3}\right].$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn25.gif) The reason behind this may be explained as follow. The modes of vibration of long wavelengths fully occupy the lattice under consideration as continuum [62]. However, under passable high temperature value, it follows
The reason behind this may be explained as follow. The modes of vibration of long wavelengths fully occupy the lattice under consideration as continuum [62]. However, under passable high temperature value, it follows ![$\left[{C}_{V}(T)/3R\right],$](https://content.cld.iop.org/journals/1402-4896/95/7/075705/revision2/psab8eeeieqn26.gif) and is in agreement to Dulong and Petit law [63]. The values for CV at 0 GPa and 300 K were computed to be 116.78 and 112.21 J mol−1 K for RbPdF3 and TlPdF3 respectively.
and is in agreement to Dulong and Petit law [63]. The values for CV at 0 GPa and 300 K were computed to be 116.78 and 112.21 J mol−1 K for RbPdF3 and TlPdF3 respectively.
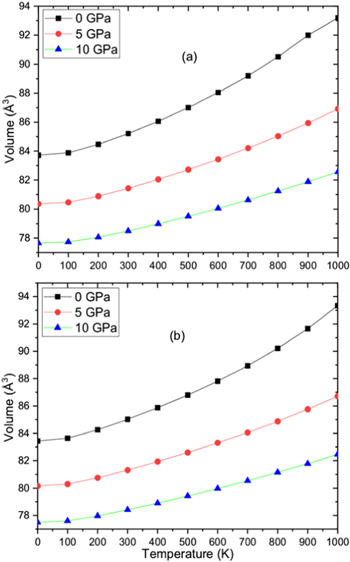
Figure 6. Variation of unit cell volume for (a) RbPdF3 (b) TlPdF3 with respect to pressure and temperature.
Download figure:
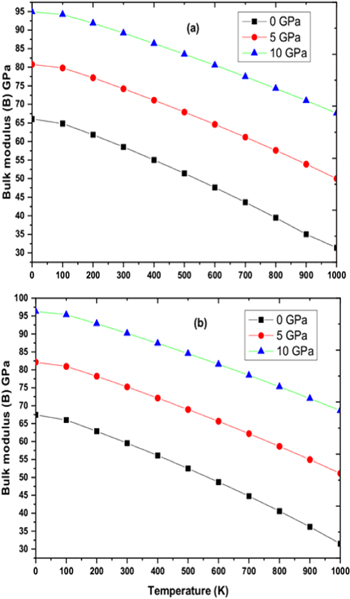
Standard image High-resolution imageFigure 7. Variation of Bulk modulus for (a) RbPdF3 (b) TlPdF3 with respect to pressure and temperature.
Download figure:
Standard image High-resolution imageFigure 8. Variation of Heat capacity Cv for (a) RbPdF3 (b) TlPdF3 with respect to pressure and temperature.
Download figure:
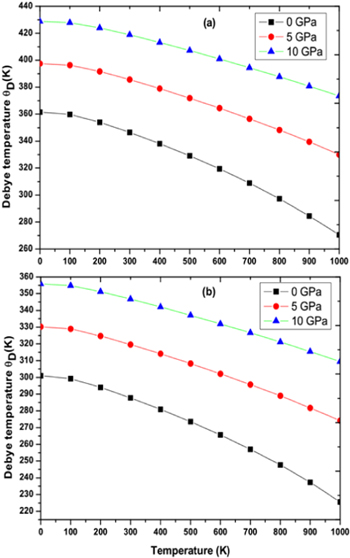
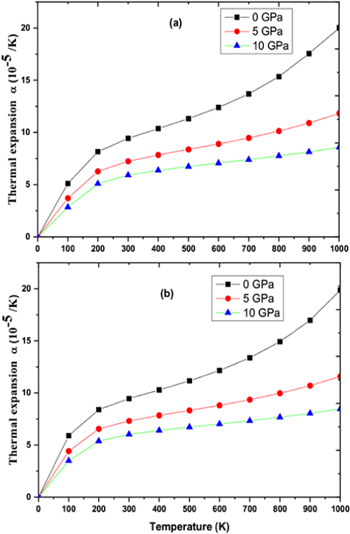
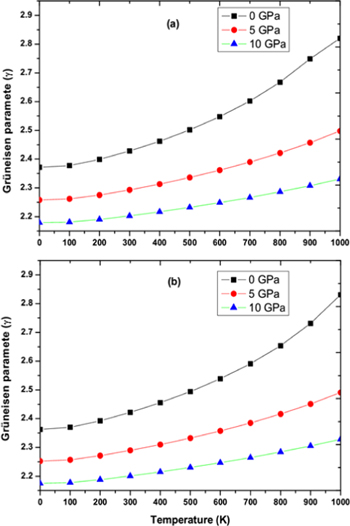
Standard image High-resolution imageDebye temperature (θD) helps to know many properties of solids like melting temperature, specific heat etc directly or indirectly. Figures 9(a), (b) shows the variation of Debye temperature (θD) with respect to pressure and temperature for RbPdF3 and TlPdF3. The (θD) is observed to decrease with rising temperature and increases with rising pressure. Calculated values of (θD) at 0 GPa and 300 K are 346 K and 287 K for RbPdF3 and TlPdF3 respectively. Further, in figures 10(a), (b), we have presented the variation of thermal expansion 'α' with varying temperature and pressure respectively for RbPdF3 and TlPdF3. 'α' for both the compounds was found to increase rapidly up to 200 K and at higher temperature 'α' is found to increase very slowly. The slow rise of 'α' above 200 K may be as a result of saturation in α up to 200 K. Grüneisen parameter (γ) designates the pressure/temperature dependence of phonon frequencies [64]. The computed γ is given in figures 11(a), (b). The value of γ at 300 K and 0 GPa is almost same and equal to 2.428 and 2.421 for RbPdF3 and TlPdF3 respectively.
Figure 9. Debye temperature as function of pressure and temperature for (a) RbPdF3 (b) TlPdF3.
Download figure:
Standard image High-resolution imageFigure 10. Termal expansion as function of pressure and temperature for (a) RbPdF3 (b) TlPdF3.
Download figure:
Standard image High-resolution imageFigure 11. Grüneisen parameter for (a) RbPdF3 (b) TlPdF3 at varying pressure and temperature.
Download figure:
Standard image High-resolution imageHence from thermodynamic parameters, we concluded that pressure and temperature have got opposite effects on the calculated parameters.
4. Conclusions
In summary, a computational code (Wien2k) based on density functional theory was used for predicting electronic, elastic, mechanical and thermodynamic nature of XPdF3 (X = Rb, Tl). The both compounds were explored as non magnetic with lattice parameters in good agreement with earlier experimental and theoretical reports. Mechanically both the compounds were indicated as ductile in nature from specific conditions of Pugh's ratio and Cauchy pressure. However, the stiffness, hardness, anisotropy, melting temperature of TlPdF3 was found comparatively large than RbPdF3. The longitudinal and transverse sound velocities of RbPdF3 were found higher than TlPdF3. The calculated electronic properties show that valence band states crosses the Fermi level as result both the compounds became metallic. In addition thermodynamic parameters were calculated in pressure rang of 0–10 GPa and temperature range of 0–1000 K. The thermodynamic examination results provided information on unit cell volume variation, thermal expansion and heat capacity for XPdF3 (X = Rb, Tl).
Acknowledgments
The author (A Mahmood) extends their appreciation to Deanship of Scientific Research King Saud University for funding the work through the research group project No. RGP-311.