Abstract
In this article, our attention is focused on the exploration of new features of the Caudrey-Dodd-Gibbon (CDG) equation arising from fluid mechanism. We introduce a constant in the transformation, which links the solution and auxiliary function defined in the bilinear form. By constructing different auxiliary function, we calculate the breather solution, one- to three-soliton solutions and lump wave solution. We report that a breather can be generated from a stripe-like soliton. We discover the soliton molecules and their interaction where the maximum amplitude will decrease as they overlap. Two types of heterotypic solitons, namely, soliton fusions and fissions are obtained by attaining their constrain conditions, respectively. We also observe this equation possesses several unique features, such as, having only the two-soliton molecules but not N (N ≥ 3)-soliton molecules, and having the line-like lump wave parallel to the x-axis but not to the t-axis.
Export citation and abstract BibTeX RIS
1. Introduction
In a real physical system, various dispersions (or dissipations) and nonlinear factors typically coexist, and their interactions can give rise to complex nonlinear effects. One such phenomenon is the solitary wave, commonly referred to as a soliton. Solitons emerge as a result of a delicate equilibrium between dispersion and nonlinearity [1–8]. The rapid development of soliton theory has been greatly beneficial, owing to its exceptionally broad and significant applications, particularly in the field of plasma physics [9, 10], nonlinear optics and optical fiber [11–16], particle and atom physics [17–19], and diverse river and ocean engineering [20–23].
In the early stages of soliton research, solitons were typically referred to as stripe-like solitary waves [1, 2]. However, as research has advanced, breathers, lump waves, and rogue waves have also been discovered [24–28]. Breathers can be considered a type of periodic solitons and are the result of two or more parallel solitons resonating in a certain phase [29–31].
In recent years, soliton molecules, various heterotypic solitons (e.g., soliton's fusions and fissions) have been identified as important features according to the soliton resonance view [32–41].
This paper will deal with the fifth order nonlinear Caudrey-Dodd-Gibbon (CDG) equation [42, 43]
with u = u(x, t) is a sufficiently often differentiable function. It has been proved that this equation is completely integrable. This means that it has multiple-soliton solutions [44]. Does it have breather, lump wave, soliton molecules and heterotypic solitons? The research motivated in this article is precisely to answer this question.
In section 2, new bilinear form is conducted. New breather and multiple soliton solutions are expressed in sections 3 and 4, respectively. The soliton molecules and two types of heterotypic solitons (namely, fusion and fission solitons) are studied in details in sections 5 and 6, respectively. Some conclusions are given in the final section.
2. The new bilinear form of equation (1)
To employing the bilinear method [45–50], ones can introduce a transformation as follow
f = f(x, t) is an auxiliary function with respect to the variables x and t, u0 is a constant.
Remark 1. Although introducing the constant u0 to u in (2) may seem like a simple operation, it plays a crucial role in the subsequent analysis, distinguishing it from previous works, such as the expression (12) in [44].
When the transformation (2) goes, equation (1) possesses the bilinear form as
where D is the bilinear operator defined by [45, 46]. while Dx and Dt are the bilinear differential operators defined by
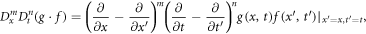
where g and h are both the functions of x and t, 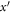 and
and 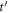 are both the formal variables, m and n are non-negative integers.
are both the formal variables, m and n are non-negative integers.
Thus, equation (1) has a general solution as (also refer [51])
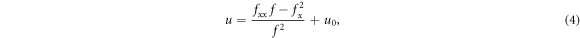
where f will be determined according to the solution's structures researched for.
3. The breather solution of equation (1)
We take f as
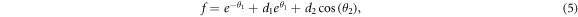
where 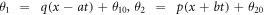 , and p, q, a, b, d1 and d2 are undetermined parameters, θ10 and θ20 are the initial phase parameters.
, and p, q, a, b, d1 and d2 are undetermined parameters, θ10 and θ20 are the initial phase parameters.
If denoting 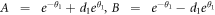 , we have
, we have
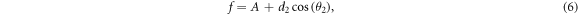
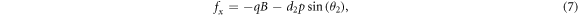
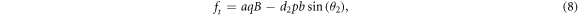
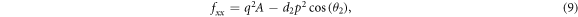
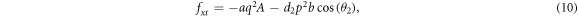
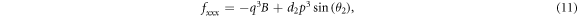
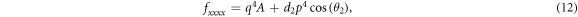
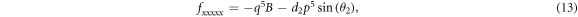

Substituting (6)–(14) into the bilinear form (3), collecting the coefficients of constant, 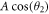 and
and 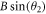 , then letting them zero, we have
, then letting them zero, we have
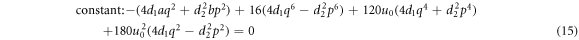
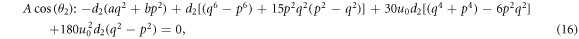
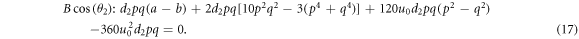
Solving the overdetermined equations (15)–(17) leads
where p, q and d2 are free parameters.
The analytic expression of the breather solution of equation (1) can be obtained by substituting (18) into (5) and then into the general solution (4). However, we will not provide its specific expression due to its lengthy algebraic form. Furthermore, we find out that a breather can be generated from a soliton by controlling the parameters. This is because the auxiliary function f by (5) contains a periodic function 'cos'. When the coefficient d2 of 'cos' tends to 0, A stripe-like soliton is obtained.
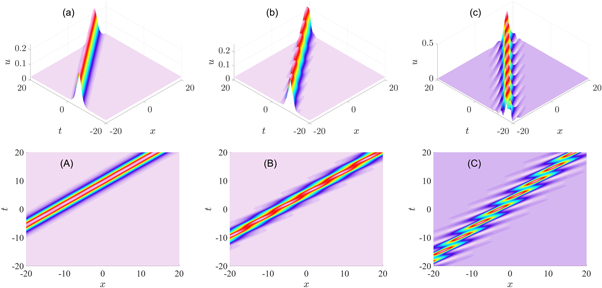
A detailed evolution from a stripe-like soliton to a breather is shown in figures 1 based on the solution (4) with (5) and (18), using the values p = 1, d2 = 1, u0 = −0.02, θ10 = θ20 = 0 and different q. It should be noted that when the third term  of f is negative in (5), it may lead to f = 0 and generate a singular solution. Therefore, careful selection of the parameters p, q, and d2 is important.
of f is negative in (5), it may lead to f = 0 and generate a singular solution. Therefore, careful selection of the parameters p, q, and d2 is important.
Figure 1. The evolution from soliton to breather given by the general solution (4) and the auxiliary function (5), and settings: p = 1, d2 = 1, u0 = −0.02, θ10 = θ20 = 0 and different q: (a) q = 0.46189; (a) q = 0.463; (c) q = 0.5; (A)-(C) are the projecting views of (a)–(c) on the x − t plane.
Download figure:
Standard image High-resolution image4. The new multiple soliton solutions
When we take f in (3) as
where ξi = ki x − ci t + ξi0, ki , ci and ξi0 are parameters, i = 1, 2, 3, ⋯ , N. Substituting (19) into (3, we get the dispersion relation as
When we choose f in (3) as
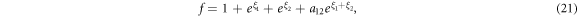
where a12 is the phase factor undetermined later.
By substituting (21) into (3), we are able to acquire
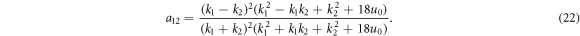
Further, the above a12 can be extended into aij with 1 ≤ i < j ≤ N as
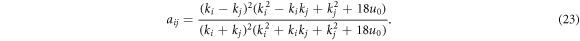
The two-soliton solution of equation (1) can be attained by substituting (21)–(22) into (4).
When ones choose f in (3) as

whrer aij is given by (23), and a123 = a12 a13 a23.
The three-soliton solution of equation (1) can be attained by substituting (24)–(23) into (4).
5. The soliton molecules
Regarding soliton molecules of the solutions obtained in section 4, we give the following proposition.
Proposition 1. When 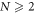 , the constraint condition for the existence of soliton molecules is
, the constraint condition for the existence of soliton molecules is

Proof. In order to make two or more solitons travel in parallel, that is, to form soliton molecules, it is required that their velocities become resonant, namely,
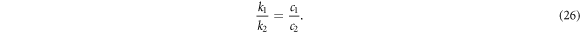
By combining (26) and dispersion relation (20), (25) can be obtained. □
Remark 2. In particular, when we set  in the transformation (2) and consider the velocity resonance condition (26), it is evident that
in the transformation (2) and consider the velocity resonance condition (26), it is evident that 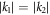 . This implies that either
. This implies that either 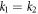 or
or 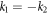 . If
. If 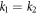 , the two-soliton solution will degenerate into a one-soliton solution. On the other hand, if
, the two-soliton solution will degenerate into a one-soliton solution. On the other hand, if 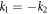 , the denominator of a12 in (22) will become zero. Therefore, the parameter u0 plays a crucial role in generating soliton molecules.
, the denominator of a12 in (22) will become zero. Therefore, the parameter u0 plays a crucial role in generating soliton molecules.
The condition (25) admits us to search for soliton molecules where two solitons propagate in parallel. More, by controlling the phase parameters ξ1 and xi2, we demonstrate the two-soliton molecules and their interactions via figure 2.
Figure 2. The soliton molecules and their interactions. The plots are given by the general solution (4), auxiliary function (21) and constrain (25), and settings: k2 = 1, u0 = −0.2, j = 0, and different ξ10 and ξ20: (a) ξ10 = 5, ξ20 = − 5; (a) ξ10 = −0.5, ξ20 = 0.5; (c) ξ10 = −1, ξ20 = 1; (d) ξ10 = −1.5, ξ20 = 1.5; (e) ξ10 = −7, ξ20 = 7. (A)–(C) are the projecting views of (a)–(c) on the x − t plane.
Download figure:
Standard image High-resolution imageGenerally, when two or multiple solitons interact in a nonlinear dynamical system, their amplitudes will change. Mostly, the maximum of the amplitudes will increase when these solitons collide or overlap. It is very interesting, when two-soliton molecules interact, the maximum of the solitons' amplitudes will increase for equation (1). When comparing the subplots (a)–(c) in figure 2, it can be observed that the maximum amplitude decreases from about 1 to 0.3.
When it comes to the soliton molecules with N ≥ 3 for equation (1), the situation becomes more complex. To address this, we propose the following proposition.
Proposition 2. When 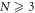 , the CDG equation (1) does not hold N-soliton molecules.
, the CDG equation (1) does not hold N-soliton molecules.
Proof. In order to explore N-soliton molecules of equation (1), we start from the three-soliton solution given by (4) and (24). It acquires
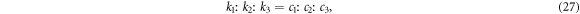
where ':' represents the division operator. By combining (27) and (25), it is seen that the three parameters k1, k2, and k3 satisfy one of the below conditions
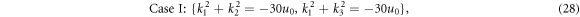
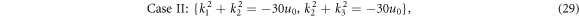
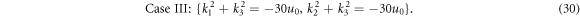
This will yield that two of k1, k2, and k3 must be equal. This implies that the three-soliton solution satisfying the condition (25) will degenerate into two parallel solitons. Thus, there are no three parallel solitons (or three-soliton molecules) for this equation. For the case of  , this conclusion is still applicable. □
, this conclusion is still applicable. □
It is worth noting that, some nonlinear equations hold N-soliton molecules, such as, optical transient stimulated Raman scattering equation [37], (3+1)-dimensional Sakovich system [40], (3+1)-dimensional Geng equation [38]. Therefore, proposition 2 is an important observation for the CDG equation (1).
6. The soliton fusions and fissions
In order to observe the soliton fusions and fissions, of equation (1), we have the following proposition.
Proposition 3. The constrain condition of the existence for the multiple soliton solutions in this work is
Proof. When the phase factor aij becomes zero, the multiple solitons will cause solitons' fusion and fission behaviors. By observing the feature of the expression of aij in (23), we get
and
Thus, the condition expression (31) is obtained. □
Remark 3. The parameter u0 also plays a crucial role in the formation of soliton fusions and fissions. If we set  , the condition (31) will not hold in the real-valued domain, indicating that there will be no soliton fusions and fissions.
, the condition (31) will not hold in the real-valued domain, indicating that there will be no soliton fusions and fissions.
For the fusions and fissions of the two-solitons, there are only two types of heterotypic structures based on the evolution of the t coordinate from small t large: (i) '1-2' structure, namely, evolution from one-soliton to two-solitons as shown in figure 3(a) and (A); (ii) '2-1' structure, namely evolution from two-solitons to one-soliton as shown in figure 3(b) and (B).
Figure 3. The bifurcations of the second-order soliton solution given by (4), (21) and (31), and settings: u0 = −0.1, ξ10 = ξ20 = 0, j = 0, and different k2: (a) 2-1 structure, k2 = 1; (b) 1-2 structures, k2 = 0.5. (A) and (B) are the projecting views of (a) and (b) on the x − t plane.
Download figure:
Standard image High-resolution imageFor the three-solitons, there are more complex and intriguing soliton fusions and fissions. In this work, we only illustrate three of them (still according to the evolution of the time variable t from small to large): (i) '3-4-3-2-4-3' structure shown in figures 4(a) and (A); (ii) '3-2-3-2' structure shown in figures 4(b) and (B); (iii) '3-2-3-2-3' structure, figures 4(c) and (C).
Figure 4. The bifurcations of the third-order soliton solution given by (4), (24) and (31), and settings: u0 = −0.1, ξ10 = ξ20 = 0, j = 0, and different k2: (a) '3-4-3-2-4-3' structure, (b) '3-2-3-2' structure, (c) '3-2-3-2-3' structure, (A) and (B) are the projecting views of (a) and (b) on the x − t plane.
Download figure:
Standard image High-resolution imageIt should be noted that these solitons' phases (e.g., heights and widths), amplitude and propagation speed before and after the soliton fusions or fissions, are significantly different. This effect indicates there are obvious the transitions of propagation directions, velocities, energies, etc. Ones can learn more interesting characteristics from figures 3 and 4.
The soliton fusions and fissions can be utilized to approximate the complex wave interaction dynamics, such as ocean interface waves. These waves are divided and merged during the motion process to form a seemingly random, yet actually regular wave pattern (as shown in figure 5).
Figure 5. Ocean surface interaction waves. The right image is the locally magnified view of the left.
Download figure:
Standard image High-resolution imageHowever, since the motion of ocean interface waves is much more complex than the dissipation and nonlinearity described by a nonlinear equation (such as the CDG equation (1)), it is reasonable to use the effect of soliton fusions and fissions studied in this article as a simplified case of the interaction effect of ocean interface waves.
7. The lump wave solution of equation (1)
If we choose the auxiliary function f in the bilinear form (3) as
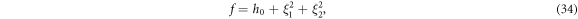
where ξi = ki x − ci t + ξi0 (i = 1, 2), ki , ci and ξi0 are parameters.
From (34), ones can derive

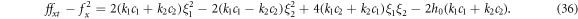
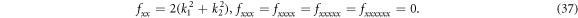
Substituting (34)–(37) into the bilinear form (3), ones can acquire the overdetermined equations as
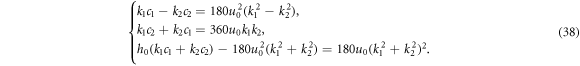
From (38), we can attain two sets of solutions about ki , ci , h0
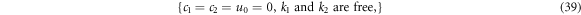
or
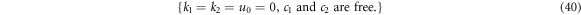
Therefore, the lump wave solution of equation (1) can be calculated from (39) as

where h0 > 0, k1, k2, ξ10 and ξ20 are free parameters. This is a line-like lump wave just parallel to the t-axis, which is shown in figure 6.
Figure 6. The lump wave solution given by (41), and settings: h0 = 1, k1 = 1, k2 = 0.5, ξ10 = 1, ξ20 = − 1. (A) is the projecting view of (a) on the x − t plane.
Download figure:
Standard image High-resolution imageSubstituting (40) into (34), then to (4) will lead trivial solution u = 0.
8. Conclusions
In this work, our attention is focused on the exploration of new features of the CDG equation (1). We introduce a constant u0 in the transformation, which links the solution and auxiliary function f defined by the bilinear form. By constructing different f, we calculate the breather solution, one- to three-soliton solutions and lump wave solution.
The main contributes of this work can be briefly summarized as follows:
- (i)Through careful research, we discover that the parameter u0 plays a decisive role in the formation of soliton molecules and soliton fusions and fissions. Due to this parameter u0, we are able to confirm the existences of the soliton molecules, soliton fusions and fissions by attaining their constrain conditions, respectively.
- (ii)We find out that a breather of equation (1) can be generated from a stripe-like soliton. The periodical function 'cos' and its coefficient involved in the auxiliary function provide a clear explanation.
- (iii)We observe the change of the maximum amplitude during the soliton molecules' interaction. In particular, the maximum amplitude decreases when they overlap. This property is rare for nonlinear dynamical systems.
- (iv)Two types of heterotypic solitons, namely, soliton fusions and fissions are obtained by attaining their constrain conditions, respectively.
- (v)Additionally, we also observe the CDG equation possesses several unique features, such as, having only the two-soliton molecules but not N (N ≥ 3)-soliton molecules, and having the line-like lump wave parallel to the x-axis but not to the t-axis.
Through this study, it is seen that the bilinear method used in this paper is an important and powerful symbolic method. Its advantage is to find multiple soliton solutions, breather, lump wave solutions and others. Its disadvantage is that the computation complexity will increase exponentially when the order of the solutions increases.
Our research and novel findings signify that the CDG equation has richer and more complex nonlinear dynamical behaviors than we had initially anticipated. Within our best knowledge, the results obtained in this work are novel and contribute to a better understanding of the CDG equation. Especially, the interaction patterns between multiple solitons, namely, various soliton fusions and fissions for the equation, have opened a window for us to comprehend and explain the complex nonlinear water wave dynamics in oceans, seas, rivers and lakes. In future works, we will explore more novel wave dynamics for this equation and other equations.
Data availability statement
The data cannot be made publicly available upon publication because they are not available in a format that is sufficiently accessible or reusable by other researchers. The data that support the findings of this study are available upon reasonable request from the authors.
CRediT authorship contribution statement
Yu-Lan Ma: Conceptualization, Software, Validation, Writingreview and editing, Methodology.
Bang-Qing Li: Methodology, Formal analysis, Data curation, Writingoriginal draft.
Compliance with ethical standards
The authors ensure the compliance with ethical standards for this work.
Conflict of interest
The authors declare that there are no conflicts of interests with publication of this work.