Abstract
Multi-microrobot control is highly promising for the assembly of matter on the microscale, in situ sensing, targeted drug delivery or nanosurgery. Magnetic micropropellers can be powered and steered by external magnetic fields and therefore represent a promising microrobotic actuation mechanism. However, the simultaneous actuation of multiple propellers along independent trajectories has yet to be realized. This is challenging, specifically because all propellers are steered by the same fields. We identify here an optimal control strategy based on a thorough theoretical analysis of multi-microrobot control. Based on analytical results and simulations, we estimate the limitations to the achievable control precisions due to diffusion, errors in the field application, and interactions between propellers. We find that control precisions of a few micrometers might be achievable.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The construction of useful robotic devices in the micrometer size range (e.g. 0.1–10 μm) is technologically promising [1]: Envisioned applications of such small machines range from microassembly [2–5] and sensing [6, 7] to minimally invasive medicine [8–11], micro-mixing [12–14] and environmental remediation [12, 15]. One established and theoretically well understood actuation mechanism for microscopic devices are rotating magnetic fields [11, 16, 17]. Two actuation strategies can be distinguished: Rolling along a surface like a wheel [5, 18–26] and the propulsion of a rigid [27–35] or flexible [36–39] chiral structure through a liquid like a propeller. Magnetically actuated devices can be used to assemble microscopic objects [2, 3, 29, 40, 41] and they can deposit material or write patterns along their trajectories, using for example catalytic patterning [42] or the recently reported nanomotor lithography [43]. For such applications, it would be advantageous if several devices could be steered independently along freely chosen trajectories. However, this task is challenging because the magnetic fields applied to steer one device will affect all the others as well. Such multi-microrobot control has previously been realized for electrostatically actuated microrobots [44], using electrostatic clamping [45], and for resonant crawling robots with distinct resonant frequencies [46], all moving along specifically patterned 2D surfaces. Using magnetic gradient fields, multi-microrobot control has been achieved on non-specialized surfaces [47] as well as in 3D [48, 49]. However, these previous approaches used magnetic objects hundreds of micrometers in size. At smaller scales, the use of magnetic gradient fields becomes increasingly unfeasible for actuation, in contrast to actuation by homogenous rotating magnetic fields (magnetic propellers) [17]. Such magnetic actuators are typically termed 'artificial bacterial flagella' [28], 'helical micromachines' [29] or variations thereof. However, we prefer the more general terms micro- or nanopropeller [27], since these actuators do not necessarily have to be either helical [33], or chiral [50, 51]. Magnetic propellers can be much smaller than objects moved with similar speeds by gradient fields and magnetic propellers close to [27] or below [33, 34] one micrometer in size have been produced and effectively actuated. Two strategies for multi-microrobot control of magnetic micropropellers have been proposed. One utilizes two different propeller types, only one of which can be actuated by a ratcheting field, whereas both rotate in a rotating field [52]. The other method, which we study here, relies on the fact that different propellers have different speed frequency relationships [11, 53, 54]. This approach was recently demonstrated experimentally by Mahoney et al [3], who showed that the non-linear speed-frequency relationship can be exploited for the individual steering of pairs of magnetic micropropellers or rollers, by actuating them below and above their critical frequencies. In addition, a theoretical analysis showed that the ratios between the propeller speeds are related to the ratios between the critical frequencies in a simple way, when actuated either at a critical frequency or at very high frequencies.
In this work, we present a more detailed theoretical analysis of multi-microrobot systems of magnetic micropropellers, based on the recently described relationship between the propeller speed and the rotation frequency [33, 55]. This relationship was also used by Mahoney et al [53]. Our analysis shows that several propellers can indeed be steered independently, provided that their individual frequency-speed relationships are characterized by different critical frequencies. By contrast, different rates at which the propellers convert rotational movement to translatory movement (denoted by  below), are not required. Most importantly, we show that it is most efficient (optimal) to actuate the propellers at their critical frequencies. Our simulations suggest that it is possible to realize multi-microrobot control with existing propeller designs, despite the limiting effects of thermal noise, errors in the measurement of propeller properties and interactions between propellers.
below), are not required. Most importantly, we show that it is most efficient (optimal) to actuate the propellers at their critical frequencies. Our simulations suggest that it is possible to realize multi-microrobot control with existing propeller designs, despite the limiting effects of thermal noise, errors in the measurement of propeller properties and interactions between propellers.
2. A model for the independent steering of magnetic propellers
Multi-microrobot control is challenging for devices actuated by rotating magnetic fields, since the actuating field is homogenous in the operating space and thus all devices are subject to identical external magnetic fields at all times. The propellers thus all move parallel to each other. A situation where microrobots move parallel to each other but with different, uncoupled speeds has already been studied theoretically and an optimal control scheme has been developed [56]. The situation we study here is more complex, since the speeds of the propellers are set by the external magnetic field and cannot be chosen independently for the different propellers. Multi-microrobot control for magnetic propellers is nonetheless possible due to the nonlinear relationship between actuating frequency 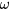 and speed
and speed 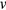 , which was discovered recently [33, 55]. This relationship has been derived for propellers in the framework of low Reynolds number hydrodynamics and is in excellent agreement with experimental data for various magnetic propellers [11, 33, 55]. In addition, it appears to be applicable to rolling magnetic devices as well [53]. The relationship is given by:
, which was discovered recently [33, 55]. This relationship has been derived for propellers in the framework of low Reynolds number hydrodynamics and is in excellent agreement with experimental data for various magnetic propellers [11, 33, 55]. In addition, it appears to be applicable to rolling magnetic devices as well [53]. The relationship is given by:

Here  is called the propulsion constant, which depends on the geometric shape of the actuated structure and
is called the propulsion constant, which depends on the geometric shape of the actuated structure and  is a critical frequency (also known as step-out frequency [29, 54]) beyond which the magnetic torque does not suffice to turn the magnetic propeller with the frequency of the actuating field. It is given by:
is a critical frequency (also known as step-out frequency [29, 54]) beyond which the magnetic torque does not suffice to turn the magnetic propeller with the frequency of the actuating field. It is given by:

where 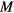 is the magnetization component perpendicular to the axis of rotation and
is the magnetization component perpendicular to the axis of rotation and 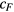 is the rotational friction coefficient of the structure.
is the rotational friction coefficient of the structure. 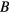 is the strength of the actuating field. Equation (1) is the starting point of our analysis and we will use it below to show that critical control is optimal. We note that while this expression is in good agreement with experimental data [33, 55], its theoretical derivation is based on assumptions, which in practice are only approximately valid. For example, the axis of rotation can depend on the frequency for certain types of propellers [57], although this does not seem to change the relationship between propeller speed and actuating frequency significantly [33].
is the strength of the actuating field. Equation (1) is the starting point of our analysis and we will use it below to show that critical control is optimal. We note that while this expression is in good agreement with experimental data [33, 55], its theoretical derivation is based on assumptions, which in practice are only approximately valid. For example, the axis of rotation can depend on the frequency for certain types of propellers [57], although this does not seem to change the relationship between propeller speed and actuating frequency significantly [33].
3. Optimal steering in the simplified case of two propellers
We first address the simplest case of controlling the 1D movement of two propellers with a constant magnetic field strength. Each micropropeller is then characterized by two properties, the critical frequency ωc (which is proportional to the external field strength) and the propulsion constant 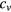 . The task we consider is to move the two propellers by given distances a1 and a2. (We use superscript numerals to distinguish the different propellers and subscript numerals to indicate a sequence of actuating fields.) Thus, we need to find a sequence of actuating conditions (frequencies ωi and durations ti of actuation) that moves both propellers to the desired position. For two actuation steps, the actuating conditions (ω1, t1) and (ω2, t2) need to satisfy the following equations:
. The task we consider is to move the two propellers by given distances a1 and a2. (We use superscript numerals to distinguish the different propellers and subscript numerals to indicate a sequence of actuating fields.) Thus, we need to find a sequence of actuating conditions (frequencies ωi and durations ti of actuation) that moves both propellers to the desired position. For two actuation steps, the actuating conditions (ω1, t1) and (ω2, t2) need to satisfy the following equations:

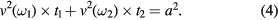
Typically there are many solutions to these equations, but as we show below not all solutions are equally useful. Two possible solutions are illustrated in figure 1: The solid lines show a solution using the critical frequencies of the two propellers, while the dashed lines show a solution with one frequency above and one below both critical frequencies. One can see that the two solutions differ in the time it takes to reach the final positions as well as in the total distance the propellers travel. The latter varies, as the propellers may need to travel back and forth in order to arrive at the intended final positions. We quantify the total time needed to reach the intended final positions by the control time  , defined as:
, defined as:

Figure 1. (a) Speed is plotted against frequency for two exemplary propellers. The dashed and solid lines mark two choices of control frequencies, one of which (the solid lines) is equal to the critical frequencies of the propellers. (b) The two propellers from panel (a) are now used for a 1D control task. The position of the propellers is plotted against time until the propellers have reached their designated end positions (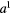 = −10 μm and
= −10 μm and 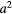 = 20 μm). The dashed lines correspond with the choice of control frequencies marked by dashed lines in panel (a). The solid lines correspond to control frequencies equal to the critical frequencies. A trajectory can obviously be split into parts to better approximate a linear trajectory from the start to the end positions. Splitting the two parts of the solid trajectory into four parts each leads to the dotted line. The meaning of the variables provided as insets is explained in the main text.
= 20 μm). The dashed lines correspond with the choice of control frequencies marked by dashed lines in panel (a). The solid lines correspond to control frequencies equal to the critical frequencies. A trajectory can obviously be split into parts to better approximate a linear trajectory from the start to the end positions. Splitting the two parts of the solid trajectory into four parts each leads to the dotted line. The meaning of the variables provided as insets is explained in the main text.
Download figure:
Standard image High-resolution imageThe extent of back-and-forth traveling is characterized by the excursion ratio 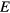 , which we define as:
, which we define as:

These expressions use the absolute values of the durations  , since formally negative and positive durations are used to denote clockwise and counterclockwise rotation, which both add positively to the control time
, since formally negative and positive durations are used to denote clockwise and counterclockwise rotation, which both add positively to the control time 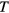 . We notice that
. We notice that 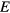 is based on the total distance traveled, not the maximal distance from a straight line between the initial and final position. The latter can be reduced by alternating between the two actuation conditions several times, as indicated by the dotted lines in figure 1(b). This scenario uses the same actuation frequencies as the solid lines, but splits the step from the initial to the final position into several (4 in this case) equal substeps. Doing so, the total duration and excursion ratio remain the same as for the solid line with only one step.
is based on the total distance traveled, not the maximal distance from a straight line between the initial and final position. The latter can be reduced by alternating between the two actuation conditions several times, as indicated by the dotted lines in figure 1(b). This scenario uses the same actuation frequencies as the solid lines, but splits the step from the initial to the final position into several (4 in this case) equal substeps. Doing so, the total duration and excursion ratio remain the same as for the solid line with only one step.
In figure 2 we plot the control time and the excursion ratio as a function of two actuating frequencies for the exemplary propellers used in figure 1. The minima for the control time as well as for the excursion ratio coincide with the choice of the critical frequencies as the actuating frequencies. Thus, while many combinations of actuating frequencies can result in the desired positioning, an optimal choice for rapid actuation as well as for minimizing back-and-forth movements is to use the critical frequencies of the two propellers. We note that the two critical frequencies need to be different, because otherwise the speeds of the two propellers will always be proportional and independent positioning will become impossible.
Figure 2. Dependence of control time and excursion ratio on the actuating frequency. (a) The speed versus frequency relationship in the case of two propellers. The critical frequencies are 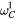 = 80 Hz and
= 80 Hz and 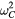 = 100 Hz. (b) The control time
= 100 Hz. (b) The control time 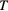 is color coded from small (red) to big (blue).
is color coded from small (red) to big (blue). 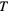 depends on the two control frequencies (
depends on the two control frequencies (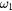 and
and 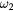 ). The global minimum is at the critical frequencies (intersection of the dashed lines). (c) The excursion ratio
). The global minimum is at the critical frequencies (intersection of the dashed lines). (c) The excursion ratio 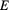 is color coded from small (red) to big (blue).
is color coded from small (red) to big (blue).  has a degenerate minimum at the critical frequencies. The dark red areas all correspond to
has a degenerate minimum at the critical frequencies. The dark red areas all correspond to 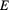 = 1, meaning that the propellers can travel to the intended end positions on a linear trajectory. The plots are symmetric around the line
= 1, meaning that the propellers can travel to the intended end positions on a linear trajectory. The plots are symmetric around the line  =
= 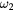 , since the problem is symmetric to exchanging the order in which the control frequencies are applied. The control time and excursion ratio landscapes are not convex and can already be quite complicated for two propellers.
, since the problem is symmetric to exchanging the order in which the control frequencies are applied. The control time and excursion ratio landscapes are not convex and can already be quite complicated for two propellers.
Download figure:
Standard image High-resolution imageSo far, we have not varied the strength of the magnetic field. However, the magnetic field strength simply rescales the critical frequencies of all propellers and thus only changes the time scale of the control task. As a consequence, an increase in the field strength results in a proportional decrease of the control time  without affecting the excursion ratio. This means that in principle any desired control time can be set by choosing a sufficiently strong field. In practice, however, it is difficult to produce strong rotating magnetic fields and the upper limit
without affecting the excursion ratio. This means that in principle any desired control time can be set by choosing a sufficiently strong field. In practice, however, it is difficult to produce strong rotating magnetic fields and the upper limit  is tens of mT for typical instrumentation. Therefore, the optimal actuation strategy to minimize the control time
is tens of mT for typical instrumentation. Therefore, the optimal actuation strategy to minimize the control time  is critical control with the strongest possible field strength.
is critical control with the strongest possible field strength.
4. Generalization to n propellers
These findings can be generalized in two ways. Firstly, critical control can be used to make propellers follow trajectories in 3D, by breaking the 3D trajectory into consecutive (possibly orthogonal) 1D steps. Secondly, our findings are also valid for higher propeller numbers: In the supplementary information (SI) (stacks.iop.org/JPhysD/49/065003/mmedia), we show that the control time and the excursion ratio are minimized when  propellers are actuated with
propellers are actuated with 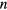 actuation steps using the critical frequencies of these propellers and the maximally producible magnetic field strength
actuation steps using the critical frequencies of these propellers and the maximally producible magnetic field strength  . We call this approach to the steering of multi-microrobot systems critical control. Again, the critical frequencies of the propellers must be pairwise distinct.
. We call this approach to the steering of multi-microrobot systems critical control. Again, the critical frequencies of the propellers must be pairwise distinct.
These findings are based on numerical optimization and random sampling, explicitly treating the cases 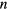 = 2 to
= 2 to  = 16. Although we currently lack a rigorous mathematical proof, we conjecture that they hold true for arbitrary
= 16. Although we currently lack a rigorous mathematical proof, we conjecture that they hold true for arbitrary  . Small changes to the functional form of the speed frequency relationship (equation (1)) most likely do not render critical control suboptimal, but it is an open question how much this relationship can be altered before critical control is not optimal anymore.
. Small changes to the functional form of the speed frequency relationship (equation (1)) most likely do not render critical control suboptimal, but it is an open question how much this relationship can be altered before critical control is not optimal anymore.
From a practical point of view, the question whether an actuation strategy is optimal in the mathematical sense is, however, less important than the actual difference in performance between actuation strategies. Thus, in figure 3, we compare the average control time for critical control with average control times obtained by using random actuation frequencies. Propeller properties and intended propeller end positions were randomly generated 10 million times in order to calculate averages (see SI)(stacks.iop.org/JPhysD/49/065003/mmedia). One can see that the control time grows extremely fast with the number of propellers ( ) if control frequencies are chosen randomly instead of equal to the critical frequencies. Thus critical control appears to be far superior to control with random frequencies and to be crucial for a practical realization of multi-microrobot systems of magnetic micropropellers.
) if control frequencies are chosen randomly instead of equal to the critical frequencies. Thus critical control appears to be far superior to control with random frequencies and to be crucial for a practical realization of multi-microrobot systems of magnetic micropropellers.
Figure 3. Comparison of control times 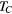 and
and  .
. 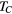 is the control time of a randomly generated control task with
is the control time of a randomly generated control task with  propellers, when using critical control.
propellers, when using critical control. 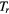 is the control time when using randomly generated control frequencies for the same control task. Both cases use the same constant magnetic field strength. Control times were calculated for
is the control time when using randomly generated control frequencies for the same control task. Both cases use the same constant magnetic field strength. Control times were calculated for 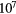 randomly generated control tasks. This was repeated for propeller numbers from 2 to 16 and the mean values of the sampled control times are plotted against the propeller number
randomly generated control tasks. This was repeated for propeller numbers from 2 to 16 and the mean values of the sampled control times are plotted against the propeller number  .
.  increases much faster than
increases much faster than  , showing that critical control is crucial for a practical realization of multi-microrobot control. A random choice of control frequencies can result in control problems that do not have a solution. The criterion used to exclude these cases (the condition number), also tends to exclude solutions with control times above
, showing that critical control is crucial for a practical realization of multi-microrobot control. A random choice of control frequencies can result in control problems that do not have a solution. The criterion used to exclude these cases (the condition number), also tends to exclude solutions with control times above  s, which is why
s, which is why  levels off.
levels off.
Download figure:
Standard image High-resolution imageIn particular, for critical control, the control time does not grow very rapidly with increasing propeller numbers and remains on the order of seconds for as much as ten propellers. The dependence of the control time on the propeller number and the task parameters can be described with a scaling relation (see the Supporting information for a derivation and numerical tests),
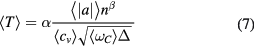
Here  denotes an average value,
denotes an average value,  and
and 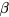 are dimensionless fit parameters and
are dimensionless fit parameters and  is a spacing parameter, which indicates how closely spaced the critical frequencies of different propellers are. Interestingly we find
is a spacing parameter, which indicates how closely spaced the critical frequencies of different propellers are. Interestingly we find 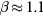 , meaning that
, meaning that 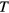 grows as
grows as 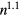 , i.e. only slightly faster than linearly with the propeller number.
, i.e. only slightly faster than linearly with the propeller number.
5. Simulations of multi-microrobot control for magnetic propellers
To demonstrate what kind of multi-microrobot tasks could be performed with magnetic micropropellers, we simulated an exemplary 2D control task, using realistic values for the propeller properties [33] and field strength and frequencies. The simulation also takes diffusion into account explicitly. For this demonstration, steric, hydrodynamic or magnetic interactions between propellers and errors in the measurement of propeller properties were neglected, as these do not pose fundamental barriers to multi-microrobot control (see below). In the exemplary control task, four propellers follow trajectories that result in intertwined pentagons (figure 4). To achieve this, the propellers take turns in crossing the intersections of the pentagons. A fifth propeller moves around the intertwined pentagons at approximately constant speed. In combination with catalytic patterning [42] or nanomotor lithography [43], steering propellers on such trajectories might be used to generate shapes of a deposited material (e.g. gold) that would be difficult or impossible to produce in conventional ways. For micron-sized propellers (1.3 μm in figure 4), diffusion is not negligible and will lead to deviations from the intended trajectory. To deal with such deviations, the actual propeller positions are measured after each actuation step, and the fields for the next step are determined such that (in the absence of diffusion) they move the propellers from their actual current positions to the next intended positions. As diffusive motion grows with the square root in time, actuation steps need to be sufficiently long to avoid that propellers solely cancel diffusion and do not advance along the intended trajectories. Therefore, the lengths of the actuation steps (and thus the next intended positions) were chosen in such a way, that the propellers outswim diffusion two-fold on average. This means that the step length is approximately twice as long as the root mean square displacement expected to occur during the control time due to diffusion. We assume that the time needed for measuring the propeller positions and calculating the actuation fields (on the order of milliseconds) is much shorter than the control time  (on the order of seconds) and can thus be neglected in the simulations. Figure 4 shows the results of simulations using three different sets of propeller properties. The precision of the trajectories is highest if the propellers have high propulsion constants
(on the order of seconds) and can thus be neglected in the simulations. Figure 4 shows the results of simulations using three different sets of propeller properties. The precision of the trajectories is highest if the propellers have high propulsion constants 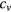 and if their critical frequencies
and if their critical frequencies  are well spaced. Based on the scaling of the control time, an analytical expression for the achievable precision has been derived, which agrees with the simulation results.
are well spaced. Based on the scaling of the control time, an analytical expression for the achievable precision has been derived, which agrees with the simulation results.
Figure 4. Visualization of simulations. Five propellers trace a pattern of intertwined pentagons surrounded by a decagon. The effective speed with which the outermost propeller travels along the trajectory is approximately constant, but different in the three cases, so that the mean magnetic field strength is equal to 1 mT. The minimum step length was adjusted so that the propellers outswim diffusion on average twice. The propeller size was set to 1.3 μm. The propeller properties for the three explored cases are displayed in panels d, e and f. The resulting propeller trajectories are displayed in panels a, b and c respectively. The red and blue lines trace the complete movement of the propellers, including excursions. The black lines trace the positions of the propellers at the end of completed actuation steps. It is apparent that well-spaced critical frequencies and high propulsion parameters increase the accuracy of the trajectories.
Download figure:
Standard image High-resolution image6. Limits to the control precision
There are three main factors that may limit the feasibility and precision of multi-microrobot control for magnetic micropropellers: diffusion of the propellers, errors in the measured propeller properties and applied fields, and (steric, hydrodynamic or magnetic) interactions between the propellers or between propellers and their physical environment.
The most obvious limitation is due to diffusion: Diffusion limits the accuracy with which several propellers can be positioned and since the diffusion coefficient is size-dependent, this means that the propellers should not be too small. On the other hand, positioning a propeller with a spatial resolution higher than its size might not be useful, so that the size itself should be considered as another limitation on accuracy, in favor of smaller propellers. Thus, these two conflicting requirements suggest that there is an optimal propeller size, for which both requirements are equally limiting. This optimal size is given by ![${{R}^{\text{opt}}}=\sqrt[3]{\frac{{{h}_{2}}\,d\,{{k}_{\text{B}}}\,T\,\alpha \,{{n}^{\beta}}}{{{h}_{1}}\,3\pi \eta \,\sqrt{\langle {{\omega}_{C}}\rangle \Delta }\,\langle {{{\hat{c}}}_{v}}\rangle}}$](https://content.cld.iop.org/journals/0022-3727/49/6/065003/revision1/daa075dieqn059.gif) (see the SI for an analytical argument based on equation (7))(stacks.iop.org/JPhysD/49/065003/mmedia).
(see the SI for an analytical argument based on equation (7))(stacks.iop.org/JPhysD/49/065003/mmedia). 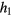 is a parameter that compares the propeller size to diffusion and
is a parameter that compares the propeller size to diffusion and 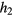 is the number of times the propellers outrun diffusion.
is the number of times the propellers outrun diffusion.
Our simulations show indeed such limitations due to diffusion for the precision of multi-microrobot control. For example, for five optimized propellers (propelling 0.2 body lengths per rotation) moving in water at room temperature, a positioning precision of around 2 μm seems to be a lower limit. This limit could be decreased by lowering the temperature and increasing the viscosity of the medium. We note that effects that diffusion could have on the propulsion of the propeller itself [58] were not included in the simulations. In particular, if the propeller is so small that rotational diffusion is significant in comparison with the rotation of the propeller due to the actuating magnetic field, deviations from our mathematical model for propeller actuation might be important. For the smallest propeller sizes discussed here (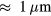 ), it is possible to construct propellers that still behave as described by equation (1) [33] and therefore, multi-microrobot control with similar accuracies as those demonstrated in our simulations seems feasible.
), it is possible to construct propellers that still behave as described by equation (1) [33] and therefore, multi-microrobot control with similar accuracies as those demonstrated in our simulations seems feasible.
Errors in the measured propeller properties can also be problematic, since the fields to be applied are calculated based on these measured properties. A sensitivity analysis of our model (see SI)(stacks.iop.org/JPhysD/49/065003/mmedia) shows that the propeller properties need to be known with an accuracy of a few percent. If this level of accuracy is achieved, the resulting propeller positioning errors are smaller than the positioning errors resulting from diffusion and can be similarly corrected for, using position measurements between actuation steps. Importantly, the effects of errors in the measured propeller properties increase only slightly with increasing number of propellers. Thus we conclude that errors in the measured propeller properties will not impose a fundamental barrier to multi-microrobot systems of magnetic micropropellers, although it will certainly be challenging to measure the propeller properties with the required precision.
Finally, interactions between propellers may become important if the propellers move in close spatial proximity. We estimate that steric, hydrodynamic and magnetic interactions are negligible if the propellers are separated by more than 5 body lengths, but may limit the ability to steer propellers along trajectories that require closer proximity (see SI)(stacks.iop.org/JPhysD/49/065003/mmedia). Interactions of the propellers with their physical surroundings (e.g. a surface on which the propellers rest) could render multi-microrobot control impossible if these interactions are irregular and unpredictable. In the case of a flat substrate, towards which the propellers gravitate, the propellers will roll along the surface in addition to their propulsive motion. At least in some cases, the rolling motion appears to be linearly related to the propeller rotation [53], just like the propulsive motion. Thus, the speed-frequency relationship for the combined rolling and propulsion movement will have the same form as equation (1), although different propellers will then move in different directions. The theory described in this paper can be generalized to rolling [53] motion and combinations of 3D propulsion and rolling on a surface, using a simple transformation which maps the physical movement of the propellers to the corresponding number of rotations (see SI)(stacks.iop.org/JPhysD/49/065003/mmedia).
Thus, the limitations of multi-microrobot control due to the three effects discussed here do not seem to impose insurmountable barriers to its practical realization. Propellers in a size range of 2–20 μm and not too close to each other can be expected to behave according to the theory described in this paper. In situations where propellers move in a complex physical environment, or close to each other, multi-microrobot control will be more difficult, but might nonetheless still be possible.
7. Concluding remarks
In conclusion, our analysis suggests that it will be possible to realize multi-microrobot control for magnetic propellers using existing micro- or nanopropeller designs, when the identified optimal control strategy is used. Propellers designed for multi-microrobot control should have the highest possible propulsion constant and well-spaced critical frequencies. Steering precisions of a few micrometers might be achievable, while higher precisions appear to be extremely challenging according to our analysis. We expect that multi-microrobot systems have the potential to greatly increase the range of microscopic structures that can be fabricated, as well as actively manipulated and controlled.
Acknowledgments
The research was supported by the Max Planck Society and the European Research Council through a Starting Grant to Damien Faivre (256915-MB2).




