Elastic properties of monolayer graphene with different chiralities

Graphene consists of a two-dimensional (2D) layer of covalently bonded carbon atoms. Due to its particular electrical, thermal, chemical and mechanical properties, graphene has attracted extensive research investigations [1–7]. The mechanical properties of graphene must be fully understood to fulfill its important application potential. However, the conventional experimental methods are very challenging for measuring the mechanical properties of graphene since it has a nanoscale lateral dimension. Currently, nanoindentation might be the only effective way to measure the mechanical properties of graphene, which is an ultralow-load indentation technique that is widely used to measure the mechanical properties of material structures at very small scales [8]. Recently, on the basis of atomic force microscopy (AFM) indentation techniques, Frank et al [9] and Lee et al [6] measured the Young's modulus and ultimate strength of multiple-layer and monolayer graphene, respectively, and they shown that graphene is one of the strongest materials, which can have a Young's modulus as high as 1 TPa. Using an instrumented nanoindenter, Zhang et al [10] also measured the elastic moduli of monolayer, bilayer and multiple-layer graphene sheets, and they shown that the elastic modulus of graphene decreases with increase of the number of layers.

Following the experimental investigations, many theoretical or numerical studies have been developed in order to further validate the ultrahigh mechanical properties of graphene. It is reported that there is nonlinear elastic behavior of graphene under in-plane tension [11, 12], temperature has little effect on the Young's modulus of graphene [13], and the in-plane properties show anisotropic features under tension [14]. Other in-plane properties of graphene have also been reported, such as tensile fracture strength [13, 14] and the buckling behavior under compression [15]. In order to match the experimental investigation, theoretical and numerical studies of the graphene indentation response have also developed [16–21]. Both theoretical and experimental studies of the indentation test of graphene are based on obtaining the indentation response (deflection) of a clamped free-standing graphene sheet to a rigid indenter tip. The elastic properties of graphene can be indirectly determined by fitting the indentation load–displacement curve using the equation [6, 16, 19]

$$\begin{eqnarray} &&P=a{\delta }_{\mathrm{t}}+b{\delta }_{\mathrm{t}}^{3}, \end{eqnarray} \tag{ 1 }$$

where P is the indentation force, δ_t is the indenter tip displacement, and a and b are fitting parameters scaled to the membrane pre-tension and the in-plane elastic stiffness. Both P and δ_t in equation (1) can be determined by experiments or computational simulations, and, thus, the two-dimensional (2D) elastic stiffness of graphene can be determined from the indentation load–displacement (P–δ_t) curve. However, equation (1) is derived from the force–displacement behavior of a clamped circular membrane under a concentrated force, in which graphene is considered to be a linear isotropic elastic material. Therefore, it is very necessary to give a theoretical analysis to show the effectiveness of this assumption. In addition, free-standing indentation is more complicated than in-plane stretching due to the van der Waals (VDW) interaction between the indenter tip and graphene, which might significantly affect the elastic properties of graphene.

The general chirality effect on the mechanical properties of carbon nanotubes (CNTs) has been reported [22, 23], while the general chirality effect on the properties of graphene monolayer is still not clear. Currently, the chirality effect of graphene is only investigated under in-plane stretching and the chiralities are limited to the armchair and zigzag structures [12, 24]. Therefore, study of the general chirality effect on the elastic properties determined from free-standing indentation is still lacking. The aim of the present work is to show the effect of chirality (not limited to zigzag and armchair structures) on the elastic properties of graphene, such as the second-order elastic stiffness, the third-order nonlinear elastic constant and the Poisson's ratio. Since the free-standing indentation is the only effective way to measure the elastic properties of monolayer graphene in experiments, both of the loading modes (including in-plane stretching and free-standing indentation) are considered in the present work, which can also help us to understand the effect of the graphene chirality on the elastic properties of graphene.

With the development of better force field and numerical algorithms, molecular mechanics simulations have been shown to play an important role in revealing precise constitutive mechanisms of nanotubes [25, 26], nanowires [27] and nanofilms [28] as well as other materials at the nanoscale. Unlike for molecular dynamics (MD) simulations, the temperature effect is neglected in molecular mechanics (MM) simulations. Since it was reported that the elastic modulus of graphene is not very sensitive to temperature [13], MM simulations are employed in the present work to study the indentation response of graphene.

The initial structures of free-standing graphene are optimized using the COMPASS force field [29], which has been used in the commonly used molecular dynamics simulation software, such as LAMMPS and Material Studio. The COMPASS force field is the first ab initio force field that enables an accurate and simultaneous prediction of various condensed phase properties of organic and inorganic materials, which has been also widely used in studying carbon type materials [17, 25, 30–32]. In order to simulate the graphene sheet and to avoid the edge effect, the periodic boundary condition is applied on the graphene monolayer under in-plane stretching; under free-standing indentation, the periodic boundary condition is applied on the lateral direction (shown as the y-direction in figure 1) and a large graphene length L ≈ 18 nm is used according to the different chiralities. The size effect of the graphene monolayer on the elastic properties has been checked under in-plane tension and the elastic properties are not sensitive to the size of the graphene monolayer. The graphene atomic lattice has sixfold rotation symmetry, and a chirality angle θ can be used to describe the graphene in-plane orientation: 0° ≤ θ ≤ 30°, where θ = 0°,30° corresponding to the zigzag and armchair structures, respectively (as shown in figure 1). In the present work, cases of graphene with other different chirality angles are also investigated: 6° ≤ θ ≤ 24°. To simplify the interaction between the indenter tip and graphene and show the intrinsic indentation behavior, we select a cylindrical indenter tip instead of using a pyramidal or spherical tip, which can create a uniaxial strain loading condition. The indenter tip is modeled by a layer of rigid carbon atoms which are uniformly distributed on a cylindrical surface; the axis of the cylinder is parallel to the lateral direction of the graphene (y-direction). The ratio of the graphene length to the indenter tip radius (L/R) is selected as L/R ≈ 30 for all different chiralities.

Zoom In Zoom Out Reset image size

Uniaxial stress stretching is applied by gradually increasing the longitudinal dimension of the graphene film and decreasing the lateral dimension, which is determined by energy minimization (as shown in figure 1(d)). The uniaxial strain stretching is realized by gradually increasing the longitudinal dimension of the graphene film but with a constant lateral dimension. In order to match the experimental results of Lee et al [6] and the theoretical results of Cadelano et al [12], we select two different tensile strain ranges (2% and 5%) to fit the elastic properties of graphene. The free-standing indentation process is displacement controlled in MM simulations. The maximum indentation displacement is selected roughly corresponding to the same tensile strain range. The indenter tip is given a constant displacement increment and the correspond interaction force P is created by the VDW interaction between the indenter tip and graphene. From the indentation load–displacement curves computed from MM simulations, the elastic stiffness is extracted. The atoms at the edge of graphene sheet are fixed to model the clamped boundary condition.

It has been reported that graphene has the nonlinear strain–stress relationship σ = Eε + Dε², where E is the second-order elastic stiffness, and D is the third-order elastic modulus [6, 12]. The strain energy density u can be expressed as [12]

$$\begin{eqnarray} u&=&\frac{E}{2}\left [\frac{1}{1+\nu }{\varepsilon }_{\alpha \alpha }{\varepsilon }_{\beta \beta }+\frac{\nu }{1-{\nu }^{2}}{\varepsilon }_{\alpha \beta }^{2}\right ]\nonumber\\ &&+~\frac{1}{2}[{\Lambda }_{1}({\varepsilon }_{\alpha \alpha }^{3}+{\varepsilon }_{\beta \beta }^{3})+{\Lambda }_{2}{\varepsilon }_{\alpha \alpha }{\varepsilon }_{\beta \beta }{\varepsilon }_{\alpha \beta }+{\Lambda }_{3}{\varepsilon }_{\alpha \beta }^{3}] \end{eqnarray} \tag{ 2 }$$

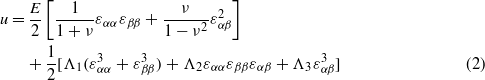
where α,β = x,y for 2D membrane, and Λ_i (i = 1–3) are the nonlinear elastic coefficients. For uniaxial strain stretching, equation (2) can be simplified to

$$\begin{eqnarray} &&u=\frac{1}{2}\frac{E}{1-{\nu }^{2}}{\varepsilon }_{m}^{2}+\frac{1}{6}{c}_{m}{\varepsilon }_{m}^{3}, \end{eqnarray} \tag{ 3 }$$

where c_m is the third-order elastic constant along the loading direction m. For uniaxial stress stretching, equation (2) can be simplified to

$$\begin{eqnarray} u&=&\frac{1}{2}E{\varepsilon }_{m}^{2}+\left [\frac{1}{6}(1+3{\nu }^{2}){c}_{m}\right .\nonumber\\ &&\left .-~\frac{1}{6}{\nu }^{2}(3+\nu ){c}_{n}-2 \nu (1-\nu ){c}_{m n}\right ]{\varepsilon }_{m}^{3} \end{eqnarray} \tag{ 4 }$$

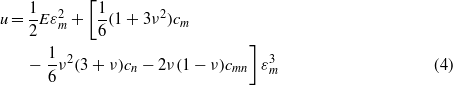
where c_n and c_mn are third-order elastic constants too, and n is the direction normal to the loading direction m. If the nonlinear effect is neglected, the strain energy density for uniaxial strain/stress stretching can be simplified to

$$\begin{eqnarray} &&u=\frac{1}{2}{E}_{\mathrm{e}}{\varepsilon }_{m}^{2} \end{eqnarray} \tag{ 5 }$$

where E_e is equal to E_l or E_l/(1 − ν²) for uniaxial strain or uniaxial stress stretching, respectively. The subscript l represents the linear strain–stress relationship assumption.

Under free-standing indentation, the indenter tip deflects the film downwards to stretch it; the work done by the indenter tip will cause a system potential energy density change (Δu), which includes two parts: the strain energy density of graphene (u_g) and the change of the VDW interaction energy density between the indenter tip and the graphene (u_VDW) which includes the initial VDW interaction energy density u₀ and the variation of the VDW interaction energy density Δu_VDW with the indentation displacement:

$$\begin{eqnarray} &&\Delta u={u}_{\mathrm{g}}+{u}_{0}+\Delta {u}_{\mathrm{VDW}}. \end{eqnarray} \tag{ 6 }$$

Denoting the indentation force acting on graphene as P, the work done by the indenter tip should be equal to the system energy change, which leads to

$$\begin{eqnarray} &&\Delta u=A\int \nolimits _{0}^{{\delta }_{\mathrm{t}}}P \hspace{0.167em} \mathrm{d}{\delta }_{\mathrm{t}}\tqs \text{or}\tqs P=\frac{1}{A}\hspace{0.167em} \mathrm{d}\Delta u/\mathrm{d}{\delta }_{\mathrm{t}} \end{eqnarray} \tag{ 7 }$$

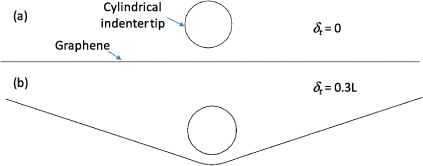
where δ_t is the indenter tip displacement and A is the area of the graphene sheet. Typically, u_VDW can be neglected in the classic free-standing indentation analysis, and Δu ≈ u_g. The tensile strain can be calculated from the length of deformed graphene (as shown in figure 2).

Zoom In Zoom Out Reset image size

3.1. Uniaxial stretching

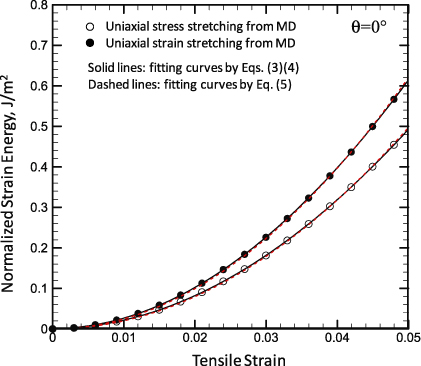
The relationships between the strain energy density (u) and the tensile strain (ε) of graphene with the chirality angle θ = 0° under uniaxial strain/stress stretching are shown in figure 3, separately. For monolayer graphene, u = U/(WL), where U is the strain energy, and W,L are the width and length of the graphene, respectively. The fitting curves on the basis of equations (3) and (4) are displayed as solid lines in figure 3, the MM results are displayed as the circular symbols, and the dashed lines are the results from fitting equation (5). The MM results can be perfectly fitted with either equations (3) and (4) or equation (5). On the basis of the strain ratio of the lateral direction to the loading direction obtained from the uniaxial stress results, the Poisson's ratio ν of graphene can be determined, as shown in figure 4. The solid line in figure 4 is the average linear fitting curve. The Poisson's ratio ν of graphene is essentially not sensitive to θ, and slightly decreases with the tensile strain ε: ν = 0.456 ±0.008 for θ = 0°–30° with ε ≤ 0.05, which can be considered as a constant for monolayer graphene. Graphene is made of C–C covalent bonds with a hexagonal distribution, and the bond angle is about 120° for undeformed structure. Under stretching, the bond angle will change to help graphene to elongate along the loading direction, since the bond angle variation required much lower potential energy than the bond stretching. Under the uniaxial stress stretching, the bonds along the loading direction are elongated, while those normal to the loading direction are shortened. The shortened bonds as well as the bond angle change will cause the Poisson's effect, as shown in figure 1(d).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The ν obtained in the present work essentially agrees well with that reported by Reddy et al [33], Arroyo et al [34] and Huang et al [35] (∼0.42), but it is higher than the value calculated by the ab initio calculation [36] as well as the one used by Lee et al [6], which is about 0.17. This difference may be caused by the small computational cell size used in the ab initio calculation. In the ab initio calculation, the computational cell size is small and thus the effect of the boundary condition might affect the simulation results [35].

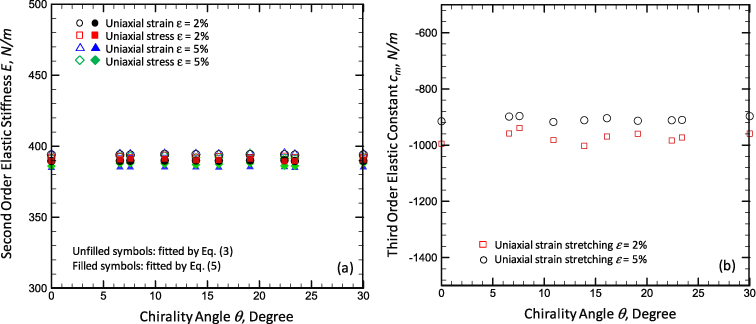
Under the uniaxial stretching, the second-order elastic stiffness (E or E_l) fitted using equations (3)–(5) for graphene with different chirality angles are shown in figure 5(a). The value of E (or E_l) from the uniaxial strain stretching is calculated from the Poisson's ratio ν = 0.46 determined from figure 4. There is a very good agreement between the elastic stiffness determined from the uniaxial stress stretch and the uniaxial strain stretch, which also proves the correctness of the Poisson's ratio obtained in the present work. For both strain ranges (2% and 5%), the values of E (or E_l) are essentially not sensitive to the chirality angle and the monolayer graphene can be considered as the isotropic membrane. In addition, the difference between E and E_l is less than about 3% (E > E_l) for all different chiralities under uniaxial stretching, which means that the linear strain–stress relationship assumption can cause less than 3% underestimation of the second-order elastic stiffness. This difference decreases with ε and thus the nonlinear effect can be neglected in the present loading range. Comparing the results fitted from the two different strain ranges, we see that the value of E is not sensitive to ε, while E_l fitted from ε ≤ 2% is slightly higher than that fitted from the range of ε ≤ 5%, which shows that graphene is a strain-softened material. This may also provide one possible reason for the value of E reported by Cadelano et al [12] being lower than that reported by Lee et al [6].

Zoom In Zoom Out Reset image size

In the present work, the second-order elastic stiffness E = 391–395 N m⁻¹ was calculated from MM simulations, which is slightly higher than the reported in-plane elastic stiffness [15, 33, 37, 38] (E = 312–384 N m⁻¹). If we use the linear strain–stress relation assumption, E = 381–385 N m⁻¹, which is close to the upper limit of the reported results. In addition, the properties calculated from the MM correspond to the properties at 0 K, typically larger than the room temperature ones.

The third-order nonlinear elastic constant (c_m) of monolayer graphene is also essentially not sensitive to the chirality angle θ of graphene under uniaxial stretching, as shown in figure 5(b). c_m < 0 means that graphene is a strain-softened material with a higher tensile strain. c_m is slightly higher for a small fitting range (ε ≤ 2%) than that from a larger fitting range (ε ≤ 5%). This result shows that the strain-softening effect gradually decrease with the increase of the tensile strain. The present results for c_m of the graphene monolayer with the chiralities of armchair and zigzag are lower than the values reported by Cadelano et al [12], which may be caused by the smaller graphene monolayer size used in the tight-binding model. Therefore, the nonlinear elastic property of graphene is not obvious, with a small tensile loading range (ε ≤ 5%).

3.2. Free-standing indentation

In classic indentation analysis, the indentation response of the free-standing film with the clamped boundary condition is quite similar to that under in-plane stretching [6], in which the stretching is created by the film deflection induced by the indenter tip. However, it should be noted that the VDW interaction between the indenter tip and the graphene has a strong effect on the indentation response since graphene is a monolayer of carbon atoms, which is not considered in continuum mechanics.

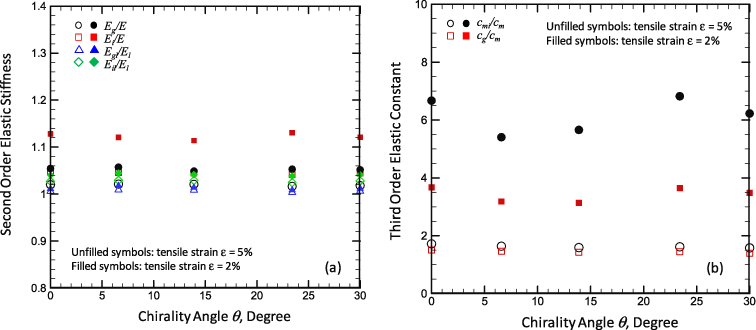
Under the free-standing indentation, the MM simulation results for the graphene monolayer cannot well be fitted using equations (3) and (5) due to the effect of the VDW interaction (represented by u₀ and Δu_VDW), and, thus, the second-order elastic stiffness E (or E_l) cannot be effectively obtained from the classic indentation analysis. After considering the VDW effect (introducing u₀ and Δu_VDW into equations (3) and (5)), the second-order elastic stiffness E_i (or E_il) can be fitted (the subscript 'i' represents indentation). The results for graphene with different chirality angles normalized by the corresponding values obtained from the in-plane tension are shown in figure 6(a). Similar to the results under the uniaxial stretching, E_i (or E_il) is essentially not sensitive to the chirality angle θ. However, the values of E_i (or E_il) are higher than those determined from the uniaxial stretching, and this difference increases with the decrease of the loading ranges (i.e., the fitting strain range). For the larger fitting strain range (ε ≤ 5%), E_i/E ≈ 1.05, which means about by 5% overestimation of the value of E; the ratio of E_il/E_l ≈ 1.03. For the small fitting range (ε ≤ 2%), E_i/E ≤ 1.13, i.e., compared with the uniaxial stretching, E will be overestimated by up to about 13% from the free-standing indentation case; the ratio of E_il/E_l ≤ 1.05. In addition, the ratio of E_i/E_il can be up to 1.1 with ε ≤ 2% (higher than that with a larger strain range, E_i/E_il ≈ 1.05 with ε ≤ 5%), which means that the nonlinear effect is much larger than that in in-plane stretching and it increases with decrease of the loading range. Therefore, under free-standing indentation with a small tensile strain fitting range, the second-order elastic stiffness E can be significantly overestimated (e.g., up to 13%), and the linear strain–stress assumption can also cause a larger error (e.g., up to 10%). Those influences do not depend on the chirality angle of the graphene.

Zoom In Zoom Out Reset image size

Due to the VDW effect, the free-standing indentation results cannot be fitted using equation (3), and, thus, the third-order nonlinear elastic constant (c_mi) cannot be determined from the classic indentation analysis (i.e., equation (3)). After considering the effect of the VDW interaction (i.e., introducing u₀ and Δu_VDW into equation (3)), the values of c_mi for the monolayer graphene with different chiralities determined from the free-standing indentation are as shown in figure 6(b). In the figure, c_mi is normalized by the corresponding value determined from in-plane tension c_m. For the larger fitting range (ε ≤ 5%), c_mi is not sensitive to the chirality angle θ and the values of c are larger than their counterparts determined from in-plane stretching (e.g., c_mi/c_m ≈ 1.55). For the smaller fitting range (ε ≤ 2%), c_mi is significantly increased (e.g., c_mi/c_m ≈ 6; the increase of the average value of c_mi is about six times that of its counterpart determined from uniaxial stretching), and c_mi is also not sensitive to the chirality angle θ, but has a larger fluctuation. Therefore, the third-order nonlinear elastic constant (c_mi) cannot be effectively determined by free-standing indentation, and the error created will decrease with increasing loading range.

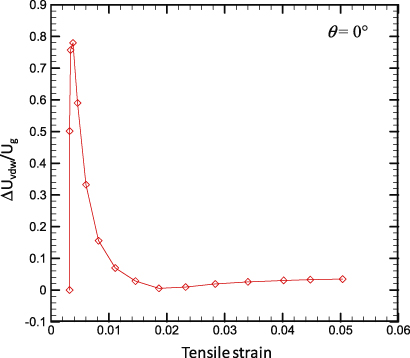
The above differences between the elastic properties determined from uniaxial stretching and those from free-standing indentation arise mainly from the VDW interaction between the indenter tip and the graphene in free-standing indentation. According to equation (6), we typically neglect the contribution from the VDW interaction and simply consider the potential energy change of the whole system as the strain energy of graphene in free-standing indentation. This simplification has a very small effect on the second-order elastic stiffness, but significantly affects the value of the third-order nonlinear elastic constant. The ratio of the VDW interaction energy change (ΔU_VDW) to the strain energy of graphene (U_g) varying with the tensile strain (ε) is shown in figure 7. This shows that ΔU_VDW/U_g rapidly decreases with increase of ε, and the contribution of the VDW interaction to the overall potential energy is large at small ε and cannot be neglected. The maximum value of ΔU_VDW/U_g represents the indentation position with the largest VDW interaction energy between the indenter tip and the graphene, which is also the position with the lowest total potential energy (i.e., the minimum value of Δu in equation (6)).

Zoom In Zoom Out Reset image size

After decoupling the VDW effect, the elastic properties of graphene determined from pure graphene deformation (E_g,E_gl and c_g) were also displayed in figures 6(a) and (b). E_g/E (or E_gl/E_l) is closer to 1 than E_i/E (or E_il/E_l) and E_g is closer to E with a larger ε, which clearly shows that the VDW effect will overestimate the value of E in the free-standing indentation, and this overestimation will be larger for a smaller loading range due to a larger VDW effect with a smaller loading range. E_g is also not sensitive to θ, and, thus, the VDW effect on the second-order elastic stiffness is not sensitive to θ. There is the similar result for the third-order nonlinear elastic constant: c_g/c_m is lower than c_mi/c_m, especially for a smaller loading range (e.g., ε ≤ 2%), and c_g is also not sensitive to θ, and, thus, the VDW effect on the third-order nonlinear elastic stiffness is not sensitive to θ.

In summary, the elastic properties from free-standing indentation are less accurate than those determined from uniaxial stretching, but free-standing indentation provides the only effective way to determine the elastic properties of graphene experimentally. Therefore, understanding the elastic behavior of graphene under free-standing indentation is very much necessary. Due to the VDW effect, a relatively large tensile strain range (e.g., 5%) is required in order to get more accurate elastic properties from free-standing indentation, and the linear strain–stress relation will cause less error with a relatively larger loading range. These findings contradict the commonly accepted view: the smaller load will give a more accurate result since the nonlinear effect increases with the tensile strain. In the present study range, the elastic properties of graphene monolayer (including E and c_m) can be considered to be isotropic under either in-plane stretching or free-standing indentation (with a large loading range). It should be noted that the nonlinear behavior is much stronger for the graphene monolayer under free-standing indentation with a smaller loading range.

Using MM simulations, we investigate the elastic properties of monolayer graphene with different chirality angles (θ) under both uniaxial stretching and free-standing indentation, and the effect of the loading range is also considered (e.g., two different loading ranges, 2% and 5%, are selected). The elastic properties considered in the present work include the Poisson's ratio (ν), the second-order elastic stiffness (E) and the third-order nonlinear elastic constant (c_m).

Under uniaxial stretching, both ν and E are not sensitive to θ and the monolayer graphene can be simplified as an isotropic membrane. E slightly decreases with increase of the tensile strain (ε), and, thus, graphene is a strain-softened material. The linear strain–stress relationship assumption can slightly underestimate E, by about 3%. Therefore, graphene can be approximately considered as a linear elastic membrane. If we consider the nonlinear behavior, c_m is essentially not sensitive to θ. The increase with ε shows that the strain-softening effect decreases with the magnitude of the tensile strain.

Under the free-standing indentation, both E_i and c_mi are also not sensitive to θ. However, the elastic properties determined from free-standing indentation take higher values than those obtained from uniaxial stretching, e.g., E is about 13% higher than that determined from uniaxial stretching. The effect of VDW interaction on the nonlinear behavior is significantly higher than that on the linear behavior (e.g., c_m can be up to six times larger than that determined from uniaxial stretching). In addition, the linear strain–stress relationship assumption also causes a much larger error in the free-standing indentation than that in the uniaxial stretching. The different elastic properties determined in free-standing indentation are caused by the VDW interaction between the indenter tip and the graphene. The VDW effect is also not sensitive to the chirality angle θ and rapidly decreases with increase of ε. Therefore, in order to get more accurate elastic properties of graphene from free-standing indentation, a relatively large strain (e.g. ε ≤ 5%) is typically required. The present work can help us to get a better understanding of the elastic properties of monolayer graphene.

I acknowledge the financial support provided by the seed grant of the Key National Research Foundation of China under Grant No. 2013CB933702 and the National Science Foundation of China under Grant No. 11172002.