Abstract
Shape memory alloys are a group of advanced materials that have found several industrial applications due to their interesting mechanical properties including a shape memory effect and superelasticity. In order to optimize the use of such materials in manufacturing different devices, appropriate advanced constitutive models are required. Recent experiments show that shape memory alloys exhibit an asymmetric response during tension and compression loading. In this paper, a new three-dimensional constitutive law is proposed based on microplane theory with the purpose of describing the tension–compression asymmetry. The model utilizes an equivalent stress on the foundation of second and third invariants of the deviatoric stress tensor in combination with two internal variables to distinguish between martensite volume fraction as well as martensite elastic modulus during tension and compression. The proposed model is then used to simulate uniaxial tension–compression loading in superelasticity as well as ferroelasticity regimes. The simulation results are compared with the corresponding results obtained by experiment and previous models reported in the literature, and a good agreement is observed. In addition, a four-point bending test is simulated for NiTi tubes in several cases. The predicted moment–curvature response and variations in the position of the neutral axis correlate fairly well with the experimental findings reported in the literature.
Export citation and abstract BibTeX RIS
1. Introduction
Nowadays, shape memory alloys (SMAs) are receiving a great deal of attention due to their exceptional mechanical and biological properties which make them good candidates for bone implants [1], energy absorbers [2], actuators [3, 4], and so on. The shape memory effect in these materials enables them to recover the applied deformations simply by heating them to above a specific temperature. In addition, if some amount of deformation is applied at high enough temperatures, the deformation will be totally recovered during unloading indicating superelasticity in these alloys. These phenomena happen because of the phase transformation from martensite to austenite and vice versa. In order to understand the thermomechanical behavior of SMA devices, appropriate constitutive models are required. Because these materials were first used in forms such as wires, beams, bars and rods, one-dimensional (1D) constitutive models were also developed by researchers [5–8]. By increasing the potential applications of SMAs such as load bearing implants, porous products and three-dimensional (3D) actuators, attempts for developing 3D constitutive models were also increased [9–14].
It is shown that SMAs exhibit an asymmetric mechanical behavior in tension and compression [15, 16]. To account for this intrinsic property, several 1D and 3D constitutive models have been developed. In 3D constitutive models, some transformation functions were introduced based on the first invariant of the stress tensor, I1, the second invariant of the deviatoric stress tensor, J2, and the third invariant of the deviatoric stress tensor, J3. Auricchio and Taylor [17] proposed a constitutive model to reproduce the superelastic behavior of SMAs at finite strains. To account for the pressure dependence of SMAs, they introduced a Drucker–Prager type loading function. Qidwai and Lagoudas [18] investigated various transformation functions to predict common characteristics of SMAs. To assess tension–compression asymmetry, they analyzed constitutive models in which J2, J2−I1, J2−J3, and J2−J3−I1 transformation functions were employed. Auricchio and Petrini [19] presented a 3D macroscopic thermomechanical model with the ability of reproducing tension–compression asymmetry using Prager–Lode type limit surface. Bouvet et al [20] proposed a phenomenological model by taking the tension–compression asymmetry into account using a transformation function based on J2 and J3 invariants. Paiva et al [21] proposed a constitutive model to consider superelasticity, one-way and two-way shape memory effect, phase transformation due to temperature variations, internal sub-loops due to incomplete phase transformations, and tensile–compressive asymmetry. Lagoudas et al [22] used averaging micromechanical methods based on the self-consistent approximation to model the thermomechanical behaviors of polycrystalline SMAs. They assessed several transformation functions to account for the tension–compression asymmetry as well as the development of a small volumetric strain during phase transformations. Lexcellent et al [23] proposed a modeling approach within the framework of thermodynamics of irreversible processes for the anisothermal response of shape memory alloys. A transformation function based on J3 and J2 invariants was used for considering the material asymmetry in tension and compression. Saint-Sulpice et al [24] investigated the superelastic behavior of SMAs under cyclic loadings. Material asymmetry was considered by utilizing the transformation function proposed in [20]. In order to scrutinize the effects of different loading modes on the superelastic behavior of SMAs, Zhu and Due [15] carried out some experiments on NiTi specimens under pure tension, compression, and torsion. They presented a macro-constitutive model for considering the tension–compression asymmetry of polycrystalline NiTi SMAs. Chao et al [25] constructed a micromechanical constitutive model to describe the cyclic deformation of polycrystalline NiTi SMAs in tensile and compressive loadings.
Mehrabi et al [26] used the microplane theory to develop a constitutive model for tension-torsion coupling and tension–compression asymmetry in NiTi shape memory alloys. In the case of material asymmetry, they employed a modified phase diagram for uniaxial loading and chose the material parameters based on the loading direction, i.e. tension or compression. Since there is no transformation function, this method can be used only for uniaxial loading and would be inapplicable for multiaxial loadings. The idea of utilizing microplane theory was first proposed by Brocca et al [27] and has been further developed by Kadkhodaei et al [28, 29] and Mehrabi et al [30]. This constitutive modeling approach was shown to be thermodynamically consistent [31] and capable of modeling nonproportional loading paths [28–30, 32]. One of the most important features of microplane theory is its capability to generalize a 1D constitutive model to a 3D one. Therefore, one just needs the material parameters identified through a uniaxial tension (or compression) test for modeling 3D loading cycles. According to the existing findings, this modeling approach provides a simple yet powerful 3D constitutive modeling approach for SMAs. However, it is necessary to enhance it to be able to systematically consider the tension–compression asymmetric response of SMAs. In addition, it has been previously shown that the elastic modulus of the martensite phase is different in tension and compression [33]. However, the available 3D constitutive models have not addressed this behavior. The aim of this paper is to address these issues. To this end, two internal state variables are considered to distinguish between martensite volume fraction in tension and compression using a modified phase diagram and evolution functions. The obtained results in uniaxial tension–compression and four-point bending of NiTi tubes are compared with experimental results and good correlations were observed. Therefore, the proposed model can be used as an appropriate tool for modeling 3D responses of shape memory alloys considering tension–compression asymmetry.
2. Constitutive modeling
In microplane modeling, a 1D constitutive law is used for any generic plane, referred to as a microplane, passing through any material point. To generalize the 1D constitutive model to the 3D one, a homogenization process is used. Therefore, only the material parameters of the uniaxial tension (or compression) test are required for the 3D model, which makes this method of more interest. In this section, first, a 1D constitutive relation of SMAs considering tension–compression asymmetry is introduced. Then, this 1D law is generalized to a 3D model by using microplane theory and a suitable transformation function.
2.1. One-dimensional constitutive model
According to the approach proposed by Poorasadion et al [33], considering the tension–compression asymmetry, the 1D stress–strain relation of a SMA can be described using the following equation:
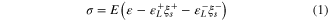
in which  and
and 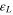 are the stress-induced martensite volume fraction and maximum recoverable strain, respectively. The superscripts '+' and '–' denote tension and compression, respectively. σ and
are the stress-induced martensite volume fraction and maximum recoverable strain, respectively. The superscripts '+' and '–' denote tension and compression, respectively. σ and  are respectively the uniaxial stress and strain, and E the elastic modulus. It is shown that the elastic modulus of SMAs is a function of the martensite volume fraction and can be written using the Reuss model as follows:
are respectively the uniaxial stress and strain, and E the elastic modulus. It is shown that the elastic modulus of SMAs is a function of the martensite volume fraction and can be written using the Reuss model as follows:

where EA and EM are the elastic moduli of full austenite and full martensite phases, respectively, and 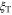 the temperature-induced martensite volume fraction. The superscript 'T' is attributed to temperature-induced quantities.
the temperature-induced martensite volume fraction. The superscript 'T' is attributed to temperature-induced quantities.
To specify the evolution of 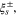 and
and  the evolution function presented by eqution (3) is utilized. This evolution function was firstly proposed by Brinson [6] and then modified by Poorasadion et al [33] to account for the tension–compression asymmetry. In this paper, this evolution function is enhanced to model the start and finish of the reverse transformation more accurately with the use of the stress-temperature phase diagram depicted in figure 1 [34].
the evolution function presented by eqution (3) is utilized. This evolution function was firstly proposed by Brinson [6] and then modified by Poorasadion et al [33] to account for the tension–compression asymmetry. In this paper, this evolution function is enhanced to model the start and finish of the reverse transformation more accurately with the use of the stress-temperature phase diagram depicted in figure 1 [34].
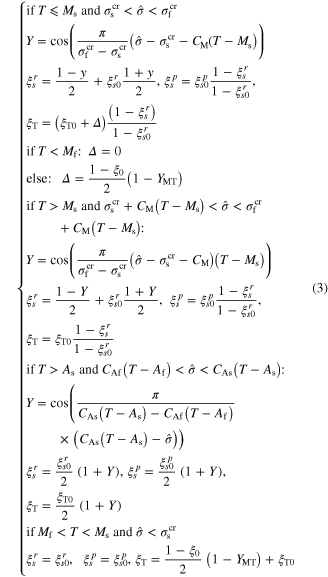
in which Mf, Ms, As, Af, and T are martensite finish, martensite start, austenite start, austenite finish, and temperature, respectively. Superscripts 'r' and 'p' are as (r = +, p = −) in tension and (r = −, p = +) in compression, 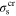 and
and  the critical start and finish stresses for martensite detwinning,
the critical start and finish stresses for martensite detwinning, 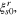
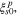 and
and  the initial values of the corresponding martensite volume fraction, CM, CAs, and CAf the slopes of the transformation strips as shown in figure 1, and
the initial values of the corresponding martensite volume fraction, CM, CAs, and CAf the slopes of the transformation strips as shown in figure 1, and 
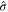 is the modified stress to account for the asymmetry in tension and compression as follows:
is the modified stress to account for the asymmetry in tension and compression as follows:
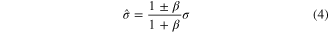
where '+' and '–' in the numerator indicate tension and compression, respectively, and β is a parameter to determine the value of asymmetry, which is defined using the following relation:
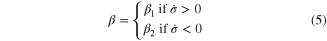
in which β1 and β2 are chosen to distinguish the asymmetry level of loading from that of unloading. The effect of β on the asymmetry level will be discussed in the following section.
Figure 1. The stress-temperature diagram for the martensite transformation of shape memory alloys.
Download figure:
Standard image High-resolution imageWhen using the phase diagram at high temperatures, if the values of 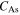 and
and 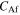 are higher than
are higher than  it should be noted that the corresponding lines may cross each other. This issue would be problematic when the critical stress of austenite finish is higher than that of martensite start or if the critical stress of austenite start is higher than that of martensite finish. Figures 2(a) and (b) demonstrate these cases, respectively. It implies some restrictions on the transformation stresses as presented by equations (6) and (7):
it should be noted that the corresponding lines may cross each other. This issue would be problematic when the critical stress of austenite finish is higher than that of martensite start or if the critical stress of austenite start is higher than that of martensite finish. Figures 2(a) and (b) demonstrate these cases, respectively. It implies some restrictions on the transformation stresses as presented by equations (6) and (7):
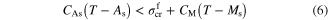
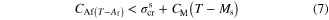
Figure 2. The stress–strain curve of an SMA when (a) the critical stress of austenite finish is higher than that of start martensite, and (b) the critical stress of austenite start is higher than that of martensite finish.
Download figure:
Standard image High-resolution imageAccording to the above-mentioned explanations and considering 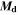 as the martensite dead temperature, the phase diagram should be used for temperatures with the constraint below:
as the martensite dead temperature, the phase diagram should be used for temperatures with the constraint below:
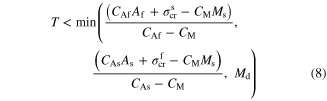
2.2. Three-dimensional constitutive model
To develop a 3D constitutive model using the microplane theory, three main steps should be followed. These steps are the projection of the macroscopic stress tensor on each microplane, the definition of a 1D constitutive law for each microplane, and the generalization of 1D constitutive laws to 3D using a homogenization process [28–31]. In this regard, a static constraint formulation with a volumetric-deviatoric split is employed in the present work. As shown in figure 3, the macroscopic stress tensor may be projected as normal and shear vectors on a microplane. The normal and shear stresses on each microplane can be described as:
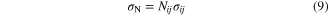
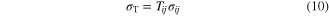
where  is the macroscopic stress tensor,
is the macroscopic stress tensor, 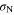 normal stress,
normal stress,  shear stress,
shear stress, 
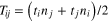 in which
in which 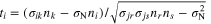 is the unit vector parallel to the resultant shear stress on the plane, and ni are the components of the unit normal vector, n, to a microplane. The normal stress is split into volumetric and deviatoric parts as:
is the unit vector parallel to the resultant shear stress on the plane, and ni are the components of the unit normal vector, n, to a microplane. The normal stress is split into volumetric and deviatoric parts as:
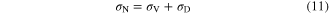
in which 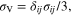
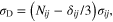 and
and 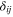 is the Kronecker delta. It is shown that using the volumetric-deviatoric split, the micro-level elastic moduli are equal to the macroscopic ones [27, 28]. It is also supposed that the martensite transformation is just associated with the shear component of microplane stresses [28, 29]. Accordingly, the volumetric and deviatoric parts are described using Hooke's law, and the shear stress can be described using eqution (1) as follows:
is the Kronecker delta. It is shown that using the volumetric-deviatoric split, the micro-level elastic moduli are equal to the macroscopic ones [27, 28]. It is also supposed that the martensite transformation is just associated with the shear component of microplane stresses [28, 29]. Accordingly, the volumetric and deviatoric parts are described using Hooke's law, and the shear stress can be described using eqution (1) as follows:
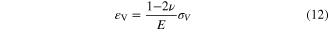
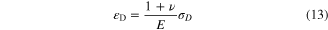
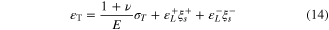
where ν is the SMAs Poisson ratio, 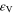 the volumetric strain,
the volumetric strain, 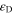 the deviatoric strain, and
the deviatoric strain, and 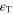 the shear strain. By applying the principle of complementary virtual work [28, 29] and some simplifications, the following relation is obtained for the strain tensor:
the shear strain. By applying the principle of complementary virtual work [28, 29] and some simplifications, the following relation is obtained for the strain tensor:
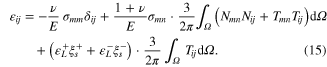
Figure 3. Projection of stress tensor as normal and shear stress vectors on each micro plane.
Download figure:
Standard image High-resolution imageTo consider the material asymmetry in tension and compression, it is necessary to define an appropriate equivalent stress to be used in equation (3) for evaluating the martensite volume fractions in equation (14). In this paper, an equivalent stress based on second and third invariants of deviatoric stress tensor (J2 and J3) is used as demonstreated below [15, 19, 22]:
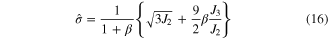
in which J2 and J3 are the second and third invariants of the deviatoric stress tensor, respectively. Note that, equation (16) reduces to equation (4) for 1D cases. Figure 4 shows the transformation surfaces for different typical values of β in the plane stress state. As it is obvious, when β = 0, the symmetric transformation surface is achieved. By increasing the value of β, the level of asymmetry will increase. According to experimental observations, the transformation surface of martensite-to-austenite and austenite-to-martensite might be of a different level of asymmetry. This can be taken into account by using different values of β presented in equation (5).
Figure 4. Transformation surface in plane–stress state for different typical values of β.
Download figure:
Standard image High-resolution image3. Results and discussion
The proposed 3D constitutive model is implented through a user subroutine UMAT in the ABAQUS comertial finite element package. To verify the model, six available experimental cases in the literature including two uniaxial tension–compression tests, two ferroelasticity problems, and two four-point bending tests of NiTi tubes are considered. One case related to subloops due to incomplete phase transformations is also investigated and the results are compared with experimenal findings. Notice that, since all the simulations are carried out at constant temperatures, there is not any temperature-induced martensite during the loading cycles. Accordingly, the value of  is optional in the nuemrical simulations.
is optional in the nuemrical simulations.
3.1. Uniaxial tests
In this subsection, the experimental tension–compression responses of superelastic NiTi samples provided by Zhu and Dui [15] (case 1) and Thamburaja and Anand [35] (case 2) are used for verification of the model. For these cases, the material is 50.8at.% NiTi and 55.96 wt.% NiTi, respectively. Tables 1 and 2 show the material parameters utilized for the determination of the stress–strain response in cases 1 and 2, respectively. These material parameters are obtained from the literature [15, 36]. Since the test temperature is above the austenite finish, the material is in the austenite phase; so, the initial value for 
 and
and  is zero for these two cases.
is zero for these two cases.
Table 1. Material parameters for case 1 [15].

|

|
|
ν |
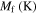
|
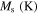
|
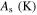
|
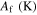
|
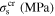
|
|---|---|---|---|---|---|---|---|---|
| 24 000 | 22 000 | 25 000 | 0.42 | 200.3 | 232.3 | 262.5 | 295.1 | 0 |
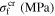
|
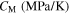
|
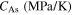
|
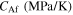
|
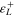
|
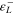
|
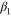
|
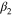
|
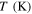
|
| 180 | 3.37 | 3.7 | 2 | 0.052 | −0.023 | 0.165 | 0.165 | 299.1 |
Table 2. Material parameters for case 2 [36].
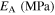
|
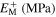
|
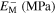
|
ν |

|
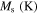
|
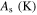
|

|
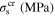
|
|---|---|---|---|---|---|---|---|---|
| 71 000 | 35 000 | 42 000 | 0.33 | 213 | 251.3 | 260.3 | 268.5 | 256 |
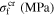
|
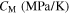
|
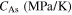
|
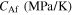
|

|

|

|
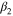
|
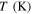
|
| 288 | 4.28 | 5.73 | 4.07 | 0.048 | -0.031 | 0.13 | 0.13 | 298 |
Figures 5 and 6 show the stress–strain response of NiTi samples in tension and compression obtained using the proposed approach, the Zhu and Dui model, and the experimental measurements [15, 35]. In all cases, the absolute values of the stress and strain are reported in compression tests. The results show a good agreement between the empirical findings and the numerical results of the present approach. In comparison with the Zhu and Dui model, the proposed model correlates better to the experimental findings especially during unloading. It is because of using the modified phase diagram (figure 1) which allows one to adjust the start and finish martensite–austenite transformation stresses more adaptively. As demonstrated in figure 5, since the elastic modulus of martensite is considered to be different in tension and compression, the proposed model is able to reproduce the experimental stress–strain response in compression more accurately. However, there is a considerable mismatch between the numerical and experimental tensile stress–strain responses at the first portion of the loading curve in figure 5. This is due to different experimental values of the austenite elastic modulus in tension and compression. In figure 5, the value of the austenite elastic modulus is calibrated using the compressive stress–strain response to be able to compare the results with those reported in [15]. Zhu and Dui [15] suggest the use of a compressive stress–strain curve to calibrate the model parameters because the transformation is more stable during unloading in the case of compression compared with tension. In addition, in all the experimental cases, there is a small amount of residual strain due to the transformation induced plasticity (TRIP) phenomenon, which can be reduced by training the SMA specimen through cyclic loading. Since the present model is not capable of considering the effect of TRIP, there is not any residual strain in the predicted stress–strain response.
Figure 5. The experimental and numerical stress–strain responses for case 1.
Download figure:
Standard image High-resolution imageFigure 6. The experimental and numerical stress–strain response for case 2.
Download figure:
Standard image High-resolution imageIn order to show the capability of the model to consider the effects of tension–compression asymmetry in ferroelastic behavior, the stress–strain responses obtained using the proposed model are compared with the numerical results reported by Jaber et al [36] (case 3) and the experimental findings for Au-47.5at.%Cd by Nakanishi et al [37] (case 4). The material parameters used for the former and the latter cases are provided in tables 3 and 4, respectively. In case 3, the temperature is below 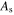 and the material is initially fully austenitic, which means the initial values of
and the material is initially fully austenitic, which means the initial values of  For case 4, the temperature is below the martensite finish temperature and the material is initially in the martensite phase which causes
For case 4, the temperature is below the martensite finish temperature and the material is initially in the martensite phase which causes 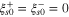 and
and  The result of the present model are compared with the previously reported findings by Jaber et al [36] and the experimental data by Nakanishi et al [37] in figures 7(a) and (b), respectively. The obtained stress–strain responses show that the present approach is in good agreement with the previously proposed model and experiments. Since the proposed model by Jaber et al [36] is not capable of considering different values for martensite elastic moduli in tension and compression as well as different values for CA, it is assumed that
The result of the present model are compared with the previously reported findings by Jaber et al [36] and the experimental data by Nakanishi et al [37] in figures 7(a) and (b), respectively. The obtained stress–strain responses show that the present approach is in good agreement with the previously proposed model and experiments. Since the proposed model by Jaber et al [36] is not capable of considering different values for martensite elastic moduli in tension and compression as well as different values for CA, it is assumed that 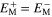 and
and  to be able to compare the results.
to be able to compare the results.
Table 3. Material parameters for case 3 [36].
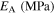
|
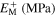
|
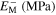
|
ν |

|
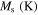
|
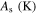
|

|
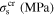
|
|---|---|---|---|---|---|---|---|---|
| 80 000 | 30 000 | 30 000 | 0.33 | 273 | 283 | 293 | 303 | 105 |

|
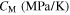
|
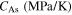
|
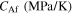
|
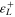
|

|
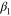
|
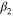
|
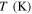
|
| 225 | 5 | 5 | 5 | 0.0615 | −0.046 | 0.186 | 0.186 | 285 |
Table 4. Material parameters for case 4 [37].

|
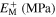
|

|
ν |
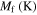
|
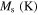
|

|
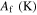
|
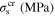
|
|---|---|---|---|---|---|---|---|---|
| 5000 | 5000 | 5000 | 0.33 | 308 | 331 | 345 | 358 | 11 |
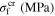
|
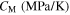
|
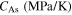
|

|

|

|
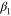
|
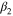
|
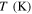
|
| 44 | 2 | 2 | 2 | 0.032 | −0.034 | −0.16 | −0.16 | 300 |
Figure 7. Comparison of the obtained ferroelastic stress–strain response with (a) numerical results reported by Jaber et al [36] and (b) experimental results by Nakanishi et al [37].
Download figure:
Standard image High-resolution imageThe stress–strain response presented in figure 7(b) shows that the model is capable of modeling subloops due to incomplete phase transformations for test temperature below martensite finish temperature. To show the ability of the model in reproducing this behavior for temperatures above austenite finish, the experimental results for 50.95at.%NiTi reported by Takeda et al [38] (case 5) are used. Figure 8 shows a comparison of the stress–strain response reproduced by the proposed model and the experimental results [38]. The material parameters utilized for this simulation are presented in table 5 and the initial conditions are as  Since the test is just performed in tension, the material parameters related to compression are not provided. Referring to figures 7(b) and 8, the present model can be used for modeling the internal subloops of an SMA in a wide range of temperatures.
Since the test is just performed in tension, the material parameters related to compression are not provided. Referring to figures 7(b) and 8, the present model can be used for modeling the internal subloops of an SMA in a wide range of temperatures.
Figure 8. Stress–strain response related to subloops due to incomplete phase transformation.
Download figure:
Standard image High-resolution imageTable 5. Material parameters for case 5.
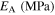
|

|
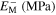
|
ν |

|
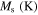
|
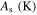
|

|
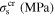
|
|---|---|---|---|---|---|---|---|---|
| 27 600 | 24 000 | NA | 0.3 | 100 | 220 | 254 | 281 | 100 |
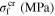
|
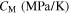
|
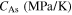
|

|
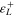
|
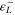
|

|

|
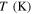
|
| 240 | 2.31 | 3.7 | 3.8 | 0.062 | NA | NA | NA | 298 |
3.2. Four-point bending of tubes
In this subsection, the proposed model is used to simulate four-point bending of NiTi tubes. First, the finite element modeling of the four-point bending is described. Then, the procedure of finding material parameters for two different cases, named cases 6 and 7, is explained. Finally, the results of the numerical simulations are presented and discussed for both cases.
Consider a tube with length L, gage length Le, outer diameter D, and thickness t as shown in figure 9(a) which depicts the schematic of the four-point bending test. The four loading points are circular rollers which hold the tube in the bending plane. Each pair of rollers is fixed to a loading wheel. These loading wheels are loaded by two cables and rotate around their center which cause bending of the tube. The magnitude of the applied moment can be calculated by measuring the force in the cable, F. A gage with length Le is attached at the middle of the tube to measure the rotation angle due to the applied moment. More information about the test apparatus and method are provided [39, 40]. As shown in figure 9(b), the mean curvature of the tube, κ, can be calculated by measuring the angles of rotation at the tube's ends (θ) and using the following equation:
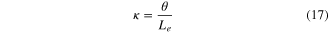
Because the problem is symmetric about the z = 0 plane, only half of the tube is modeled and appropriate boundary conditions are imposed. Referring to figure 10, a tube with length Le/2 is considered for modeling purposes because the response of the tube in the gage region is of concern. Due to the symmetry about the z = 0 plane, this plane should not move toward the z direction and the slope of the tube would be zero at this point. Accordingly, at one end (symmetry plane) of the half tube, the translational degree of freedom in the z direction and all rotational degrees of freedom are fixed. Referring to figure 9(a), the tube at the end of the gage length rotates with the angle of θ due to the applied moment. To model this rotation, at this end, a reference point is defined and all nodes of that end are tied to the reference point. A rotation about the x-axis, UR1, is applied to the reference point using the amplitude variation shown in figure 10(b). In addition, the history of the reaction moment in response to the applied amount of rotation is requested to be able to depict the moment-rotation diagrams.
Figure 9. (a) Schematic configuration of the four-point bending test and (b) illustration of the curvature calculation method.
Download figure:
Standard image High-resolution imageFigure 10. (a) Boundary conditions and loading in the four-point bending model and (b) the amplitude variation of the reference point rotation.
Download figure:
Standard image High-resolution imageIn this paper, the experimental results reported by Reedlunn et al [40] and Bechle and Kyriakides [39] are used for comparison. These experimental measurements are performed isothermally using a cold-drawn, slightly Ni-rich NiTi tube from the Memry Corporation [39, 40]. For the sake of simplicity, in the rest of the paper, the former and the latter cases are denoted by case 6 and case 7, respectively. Table 6 shows the geometric details of these two cases.
Table 6. Geometric information of cases 6 and 7.
| Dimension | Le (mm) | D (mm) | t (mm) |
|---|---|---|---|
| Case 4 | 9.58 | 3.176 | 0.318 |
| Case 5 | 76.7 | 5.11 | 0.625 |
Similar to cases 1 and 2, the test temperature is higher than the austenite finish temperature and the initial phase is austenite for cases 6 and 7. Therefore, the same initial conditions are used for these simulations. To attribute suitable material parameters to the finite element model, the experimental stress–strain response in uniaxial tension–compression is used to calibrate the required quantities. Table 7 shows the calibrated material parameters for case 6, which was performed isothermally at 298 K. Figure 11 depicts the predicted stress–strain response that correlates fairly well and is fitted to the experiment.
Table 7. Material parameters obtained by calibration of stress–strain response in tension and compression for case 6.

|
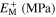
|
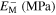
|
ν |
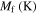
|
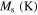
|
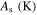
|
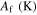
|

|
|---|---|---|---|---|---|---|---|---|
| 65 300 | 28 000 | 87 000 | 0.45 | 126 | 210 | 248 | 292 | 90 |

|
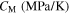
|
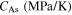
|

|
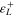
|
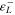
|

|
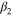
|
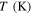
|
| 170 | 3.65 | 4.5 | 32 | 0.054 | −0.035 | 0.23 | 0.23 | 298 |
Figure 11. The experimental and numerical stress–strain curve of NiTi tube in tension and compression for case 6.
Download figure:
Standard image High-resolution imageSince the experiments of case 7 are performed at several different temperatures, it is reasonable to develop the phase diagram for the tube used by Bechle and Kyriakides [39]. The reported uniaxial stress–strain responses at 286, 296, and 306 K are considered, and the phase diagram illustrated in figure 12 is obtained. According to the phase diagram as well as the stress–strain response at 306 K, the material parameters reported in table 8 are determined and are utilized to study case 7. Figures 13(a)–(c) show the uniaxial stress–strain responses using the material parameters presented in table 8. The comparison of the presented numerical predictions with the corresponding experimental findings demonstrates a good correlation between the results. It is worth mentioning that the phase diagram reported in figure 12 is obtained using the stress–strain response in tension. Therefore, the predictions of the model are closer to the experimental stress–strain curve during tension in comparison with compression.
Figure 12. The obtained phase diagram for the tube used in experiments by Bechle and Kyriakides [39].
Download figure:
Standard image High-resolution imageTable 8. Material parameters obtained by calibration of the stress–strain response in tension and compression for case 7.
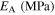
|

|
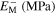
|
ν |

|
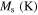
|
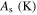
|

|
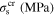
|
|---|---|---|---|---|---|---|---|---|
| 65 000 | 26 000 | 62 000 | 0.3 | 213 | 253 | 265.6 | 271.6 | 130.2 |
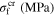
|
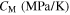
|
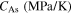
|
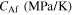
|

|
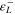
|
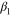
|
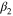
|

|
| 155 | 5.5 | 6 | 6 | 0.057 | −0.027 | 0.28 | 0.4 | 286, 296, 306 |
Figure 13. Comparison of numerical and experimental uniaxial tension–compression stress–strain responses at (a) T = 286 K (b) T = 296 K and (c) T = 306 K.
Download figure:
Standard image High-resolution imageThe rest of the paper is allotted to the modeling of four-point bending in the above-mentioned cases. The models are meshed using 20-node quadratic brick reduced integration elements denoted by C3-D20R in ABAQUS. To reduce the effects of the mesh, the number of elements was refined until a negligible change was observed in the output results. Figures 14(a) and (b) show the final meshed model for cases 6 and 7 containing 375 and 615 elements, respectively.
Figure 14. Final meshed model for (a) case 6 containing 375 elements and (b) case 7 containing 615 elements.
Download figure:
Standard image High-resolution imageFigure 15(a) shows variations of the normalized moment, MC/I, with the dimensionless curvature, 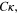 where M is the reaction moment about the x-axis, I the corresponding area moment of inertia of the cross section, C = D/2 the outer radius of the tube, and
where M is the reaction moment about the x-axis, I the corresponding area moment of inertia of the cross section, C = D/2 the outer radius of the tube, and 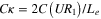 the dimensionless curvature. Figure 15(b) compares the position of the neutral axis of the tube obtained using the proposed model with the experimentally measured one [40]. In this figure, the position of the neutral axis (Y0) is measured from the centerline of the tube. In figures 15(a) and (b), a good agreement is observed for both moment and neutral axis position. The conformity is very good for small values of curvature. However, the conformity is good for higher values of curvature as well as in the unloading cycle; the predictions of the model are overestimated in these regions. This may be due to the effects of strain localization in experimental measurements as reported in [40]. Since the present model is not capable of capturing this phenomenon, it over-predicts the amount of stress in high values of curvature. In addition, the length of the tube is not long enough in comparison with its diameter, and this causes the cross sectional planes not to remain planar. However, in the utilized model, all the degrees of freedom for the loading plane are tied to a reference point meaning that the plane remains planar. Therefore, the model is over-constrained in comparison with the real sample, and the required moment is over-predicted. As another reason, the transformation induced plasticity may cause some errors in finding the appropriate material parameters, especially maximum recoverable strain. Qidwai and Lagoudas [18] stated that plastic deformations occur before full Martensitic transformation takes place. Therefore, it is not possible to obtain the maximum recoverable strain using the experimental data. This issue can be one of the reasons for the difference between experimental and numerical observations in the unloading cycle. Auricchio and Taylor [17] reported that, for the case of four-point bending, the part of the curve corresponding to the unloading and the size of the hysteresis loop differ from the experimental findings.
the dimensionless curvature. Figure 15(b) compares the position of the neutral axis of the tube obtained using the proposed model with the experimentally measured one [40]. In this figure, the position of the neutral axis (Y0) is measured from the centerline of the tube. In figures 15(a) and (b), a good agreement is observed for both moment and neutral axis position. The conformity is very good for small values of curvature. However, the conformity is good for higher values of curvature as well as in the unloading cycle; the predictions of the model are overestimated in these regions. This may be due to the effects of strain localization in experimental measurements as reported in [40]. Since the present model is not capable of capturing this phenomenon, it over-predicts the amount of stress in high values of curvature. In addition, the length of the tube is not long enough in comparison with its diameter, and this causes the cross sectional planes not to remain planar. However, in the utilized model, all the degrees of freedom for the loading plane are tied to a reference point meaning that the plane remains planar. Therefore, the model is over-constrained in comparison with the real sample, and the required moment is over-predicted. As another reason, the transformation induced plasticity may cause some errors in finding the appropriate material parameters, especially maximum recoverable strain. Qidwai and Lagoudas [18] stated that plastic deformations occur before full Martensitic transformation takes place. Therefore, it is not possible to obtain the maximum recoverable strain using the experimental data. This issue can be one of the reasons for the difference between experimental and numerical observations in the unloading cycle. Auricchio and Taylor [17] reported that, for the case of four-point bending, the part of the curve corresponding to the unloading and the size of the hysteresis loop differ from the experimental findings.
Figure 15. (a) Normalized moment versus dimensionless curvature and (b) normalized position of the natural axis versus dimensionless curvature for case 6.
Download figure:
Standard image High-resolution imageTo compare the numerical predictions with the experimentally reported results, the moment and curvature are normalized with the same method as the one used in experiments [39]. Referring to figure 13(b), suppose that 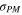 is the stress of the upper plateau, and
is the stress of the upper plateau, and 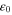 is the amount of strain at the beginning of the martensite transformation in tension at 296 K. Using these values, two quantities are defined for normalizing the moment and curvature, respectively, as
is the amount of strain at the beginning of the martensite transformation in tension at 296 K. Using these values, two quantities are defined for normalizing the moment and curvature, respectively, as  and
and 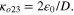 In the first quantity, D0 = D−2t is the inner diameter of the tube. Variations of the dimensionless moment with the dimensionless curvature for case 7 are depicted in figures 16(a)–(c) at 286 K, 296 K, and 306 K. The demonstrated results in this figure show the ability of the proposed model to predict the tension–compression asymmetry of shape memory alloys with good correlations with the experiment.
In the first quantity, D0 = D−2t is the inner diameter of the tube. Variations of the dimensionless moment with the dimensionless curvature for case 7 are depicted in figures 16(a)–(c) at 286 K, 296 K, and 306 K. The demonstrated results in this figure show the ability of the proposed model to predict the tension–compression asymmetry of shape memory alloys with good correlations with the experiment.
Figure 16. Variations of the dimensionless moment with the dimensionless curvature for case 7 in the temperatures of (a) 286 K, (b) 296 K and (c) 306 K.
Download figure:
Standard image High-resolution imageReferring to figures 16(a)–(c), deviation of predicted response from the experiment increases, especially in the first linear region, as the temperature decreases. In all these simulations, the material is initially in the austenite phase and this deviation would be due to variations of austenite elastic modulus. Figure 17 shows the variations of austenite elastic modulus with temperature according to the experimental stress–strain curves provided in figure 13. As is obvious, EA differs between tension and compression, which may have arisen due to the existence of some micro- (nano-) pores as well as defects in the microstructure of test samples [41, 42]. In addition, the experimental value of austenite elastic modulus increases with temperature. According to these findings, the difference between the numerical and experimental results in figure 16 can be explained. However, it should be stated that the present model cannot take different elastic moduli of austenite in tension and compression into account. Accordingly, only one fixed value is used through all the simulations. As shown in figure 17, the average value of EA of tension and compression is smaller than the value used for the simulation at the temperatures of 286 and 296 K. Therefore, the numerically predicted value of the dimensionless moment is higher than the experimental one. However, for the temperature of 306 K, the average value of EA is higher but not too far from that used for the simulation, which causes a better correlation with experimental observations. These findings demonstrate that, in order to obtain reasonable results, it is necessary to calibrate the elastic modulus of austenite based on the average value in tension and compression.
Figure 17. Variations of austenite elastic modulus with temperature.
Download figure:
Standard image High-resolution imageA comparison of the moment–curvature response for cases 6 and 7 reveals that the difference between the experiment and the presented model is larger for case 6. It might be owing to less accurate material parameters for case 6. Since there is just a uniaxial stress–strain curve at one temperature in case 6, it is not possible to find exact values of the required material parameters. However, in case 7, the existing stress–strain responses at three different temperatures makes it possible to develop a phase diagram and to find more accurate material parameters, which lead to a better correlation with experimental findings.
4. Conclusion
To account for material asymmetry in tension and compression, this paper proposes a new three-dimensional constitutive law based on microplane theory for shape memory alloys. The tension–compression asymmetry is taken into account by considering an equivalent stress based on J2−J3 invarients. Also, two internal variables are defined to distinguish between martensite volume fraction as well as elastic modulus in tension and compression. The proposed model is then used for modeling the uniaxial tension–compression, ferroelastic problem, subloops due to incomplete transformation and four-point bending of SMA tubes. The obtained results are compared with experimental and previously-reported numerical ones. In each case, the results and their discrepancy are discussed. The findings of this study show that the model predictions are in good agreement with the experimental data, as well as the previously reported results by the existing models. In the case of four-point bending, some differences are observed between numerical and experimental findings, which could be due strain localization, distortion of the tubes cross section, transformation induced plasticity, variations of austenite elastic modulus with temperature, and different values of austenite elastic modulus in tension and comperession.
Acknowledgments
All the simulations were run at the National High-Performance Computing Center of Isfahan University of Technology. The authors would also like to thank Dr Ashrafizadeh for making it possible to use the facilities of this center.


















