Abstract
Understanding the electronic structure of metal oxide semiconductors is crucial to their numerous technological applications, such as photoelectrochemical water splitting and solar cells. The needed experimental and theoretical knowledge goes beyond that of pristine bulk crystals, and must include the effects of surfaces and interfaces, as well as those due to the presence of intrinsic defects (e.g. oxygen vacancies), or dopants for band engineering. In this review, we present an account of the recent efforts in predicting and understanding the optoelectronic properties of oxides using ab initio theoretical methods. In particular, we discuss the performance of recently developed dielectric-dependent hybrid functionals, providing a comparison against the results of many-body GW calculations, including G0W0 as well as more refined approaches, such as quasiparticle self-consistent GW. We summarize results in the recent literature for the band gap, the band level alignment at surfaces, and optical transition energies in defective oxides, including wide gap oxide semiconductors and transition metal oxides. Correlated transition metal oxides are also discussed. For each method, we describe successes and drawbacks, emphasizing the challenges faced by the development of improved theoretical approaches. The theoretical section is preceded by a critical overview of the main experimental techniques needed to characterize the optoelectronic properties of semiconductors, including absorption and reflection spectroscopy, photoemission, and scanning tunneling spectroscopy (STS).
Export citation and abstract BibTeX RIS
1. Introduction
The importance of controlling the physical properties of oxide materials for present and future energy, optoelectronic and environmental technologies can hardly be overemphasized. The technological versatility of these materials is in fact outstanding. To name only a few examples relevant to renewable energy technologies, several metal oxide compounds have been suggested as promising materials to be used as photoabsorbers and cocatalysts for solar driven water splitting [1, 2], as photoanodes for dye sensitized solar cells [3], as well as in catalysis, where they can be employed both as active catalysts directly participating in the redox reactions and as inert supports for other catalysts such as metal nanoparticles [4]. The broad technological applicability of metal oxide materials, and particularly of oxide semiconductors, is made possible by their peculiar optoelectronic properties (facilitating e.g. light absorption and charge separation at energy scales relevant to redox reactions), as well as their chemical reactivity, which is enhanced by the presence of metal cations that can readily change their oxidation state, an important requirement for redox and charge transfer reactions to occur.
From a theoretical perspective, describing physical processes relevant to energy conversion technologies brings about several challenges. The first challenge is related to the heterogeneity of energy conversion materials systems, which may be represented, for example, by an interface between an oxide semiconductor and an electrolyte in the case of a photoelectrochemical cell for water splitting. How would one be able to describe, for example, the electronic structure (i.e. the level alignment between the semiconductor band edges and the redox potentials of the electrolyte) at the interface between two such chemically diverse systems, using a single, nonempirical, and accurate quantum mechanical approach? Another challenge is represented by the necessity of describing physical processes occurring at very different time and energy scales, such as light absorption and the consequent charge carrier generation in the semiconductor (the relevant time and energy scales being that of femtoseconds and electronvolts), and charge transfer at the solid–liquid interface promoted by atomic motion at room temperature (i.e. on the millielectronvolt energy scale) over typical time scales of the order of the picosecond and up to the nanosecond.
If one is interested in studying large heterogeneous systems such as solid–liquid interfaces, the use of sophisticated theoretical methods, such as many-body perturbation theory to compute the electronic structure, is often hampered by the high computational cost. One may then adopt approximate approaches in which the semiconductor and the liquid are treated separately at appropriate levels of theory, starting from the most basic density functional theory (DFT) approximations; their interaction may then be described a posteriori, treating solvation effects at different levels of accuracy, making use, e.g. of continuum solvation models [5–7]. These problems constitute the frontier of today's research in computational materials science [8], and are of great relevance to many applications, including catalysis and photocatalysis [9]. Often, however, the validation of a computational methodology for such complex systems is complicated by the lack of clean experimental data and the related difficulty of constructing realistic structural models for computational studies; moreover, defining physical quantities which may be easily compared against experimental data is not always straightforward for such complex systems. The validation problem indeed constitutes a third big challenge.
Even putting aside the complicacies related to materials heterogeneity, the task of computing accurate optoelectronic properties of oxide materials is far from trivial, although in this case the choice of the physical observables to be compared between theory and experiment can be more easily made. In this work, we provide an overview of the most recent efforts in the field of ab initio electronic structure calculations of stoichiometric and defective oxide materials, both in their bulk form and for bare surfaces. We discuss the accuracy of state of the art electronic structure methods in predicting bulk band gaps, band edge positions at surfaces, and optical transitions in defective oxides. The electronic structure methods discussed in the following sections belong either to the class of many-body perturbation theory methods in the GW approximation (section 3), which in itself may come in different flavors and with different numerical implementations, or to recently developed hybrid DFT functionals which are constructed specifically for solid state systems, namely dielectric-dependent and self-consistent hybrid functionals (section 4). The latter category of methods has the advantage of being computationally less expensive than full many body approaches, constituting an approximation to them.
When one has to determine the accuracy of ab initio methods in reproducing experiments, it is often not clear which experimental data one should use as a reference. On one hand, this issue may be related to physical effects that are missing in the theoretical description. One could think of excitonic effects and the electron–phonon renormalization of the band structure as two major causes of disagreement with experiments; in fact, these effects are often not taken into account in standard electronic structure calculations. On the other hand, the specific values of fundamental quantities such as the optical gap reported in the experimental literature are extrapolated from measured data assuming specific theoretical models. Section 2 gives an overview of the most common experimental techniques for the measurement of bulk and surface spectroscopic properties of semiconductors, dealing with the critical issue of the relationship between the raw experimental data, the theoretical model used to describe the underlying physics, and the determination of accurate numerical values for optical quantities such as the optical gap. Each section of the present work is self-contained and provides a general overview of the discussed methods. Results for oxide materials, including wide gap oxide semiconductors and correlated transition metal oxides, are then presented.
2. Experimental methods: a conceptual discussion
Reliable and meaningful experimental determination of optical properties of semiconductors critically depends on two factors. (a) Usage of up to date techniques characterized by: ample energy range, high energy and high angular resolutions, high signal to noise ratio, UHV (ultrahigh vacuum) conditions. (b) Deep enough knowledge of theory leading to the physical laws needed to extract precise and accurate numerical values from the raw data. Thus, we give here first an updated synthetic conceptual overview of state of the art spectroscopic techniques for the measurement of optical and electronic properties of oxide semiconductors, including reflection and absorption spectra, photoemission and, particularly for very thin films and surfaces, scanning tunneling spectroscopy (STS). The present is not to be intended as a complete and detailed technical description of experimental setups for which the reader can consult many excellent textbooks and papers, e.g. Yu and Cardona [10].
The generally complex and intriguing experimental dependence of the main absorption edge on photon energy is then used to illustrate how much experiments and theory are entwined (the experimental findings are 'theory laden') making questionable (or too reductive) such an apparently simple concept like that of 'optical band gap'. The positive counterpart of this experimental richness and complexity is its feedback role in stimulating new theoretical views as recently confirmed in the case of TiO2 anatase [11]. This last role of experiments is of crucial relevance for the present paper whose theoretical approach goes far beyond the mean field single electron band structure effects. The present review is limited to linear optics (linear macroscopic polarization response to applied wavy electromagnetic fields and, correspondingly, only one photon of the exciting light beam involved in the underlying microscopic processes).
The fundamental macroscopic (measurable) optical response is lumped [10] in the frequency dependent complex electric susceptibility tensor 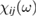 relating the Fourier transforms of the polarization vector P(ω) and of the electric field E(ω):
relating the Fourier transforms of the polarization vector P(ω) and of the electric field E(ω):
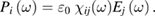
The tensor  is symmetric due to Onsager theorem and has the property
is symmetric due to Onsager theorem and has the property 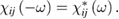
Here we have neglected spatial dispersion (wavevector dependence of 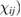 , even though it has been proved to be relevant in some cases [12]. Coherently, electric dipole approximation is understood for all waves. To simplify the notation, we will refer to the isotropic case only (cubic crystals) for which the tensor reduces to a single complex function of frequency
, even though it has been proved to be relevant in some cases [12]. Coherently, electric dipole approximation is understood for all waves. To simplify the notation, we will refer to the isotropic case only (cubic crystals) for which the tensor reduces to a single complex function of frequency 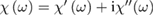 , even though many relevant semiconducting oxides are not cubic (namely TiO2 anatase and rutile). Introducing the complex relative dielectric function
, even though many relevant semiconducting oxides are not cubic (namely TiO2 anatase and rutile). Introducing the complex relative dielectric function 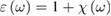 and considering that, for nonmagnetic materials, the complex refractive index is
and considering that, for nonmagnetic materials, the complex refractive index is  , we can introduce the two main laws suitable to experimentally determine the optical properties. First the normal reflectance of a semi-infinite crystal in vacuum:
, we can introduce the two main laws suitable to experimentally determine the optical properties. First the normal reflectance of a semi-infinite crystal in vacuum:
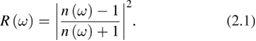
Second, the exponential decay of the intensity I of the light wave propagating in the medium along direction x > 0 beyond the outer surface at x = 0:
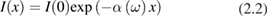
where  is the absorption coefficient
is the absorption coefficient 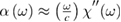 and
and  is the optical penetration depth. Then the energy balance equation for the electromagnetic energy density gives us the bridge between the macroscopic quantity
is the optical penetration depth. Then the energy balance equation for the electromagnetic energy density gives us the bridge between the macroscopic quantity 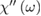 and the microscopic quantum transitions from initial states of energy Ei and final states of energy Ef with absorption of a photon with energy
and the microscopic quantum transitions from initial states of energy Ei and final states of energy Ef with absorption of a photon with energy 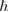 ω
ω
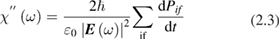
where the 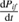 are the quantum probabilities per unit time of the above transitions. While the real part
are the quantum probabilities per unit time of the above transitions. While the real part 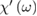 can be obtained using the first of Kramers and Kroenig equations, expressing the time invariance and causality of the dynamical polarization response:
can be obtained using the first of Kramers and Kroenig equations, expressing the time invariance and causality of the dynamical polarization response:
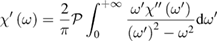
where 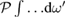 means a principal value integral. In principle the goal of theoretical predictions of, e.g.
means a principal value integral. In principle the goal of theoretical predictions of, e.g. 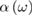 should be to reproduce the average experimental spectral behavior of this observable at all accessible frequencies apart from the (today achievable) small instrumental errors. So far, this goal has never been perfectly achieved even in the rather simple case of cubic direct-gap semiconductors like GaAs. Yet noticeable overall agreement for characteristic spectral features of the main absorption band, like van Hove singularities (including the main absorption edge, see below, and pre-band excitonic peaks, together with other many body effects) is often reached, sometimes with very good numerical estimates of optical band gap values from the fitted shape of the main absorption edge.
should be to reproduce the average experimental spectral behavior of this observable at all accessible frequencies apart from the (today achievable) small instrumental errors. So far, this goal has never been perfectly achieved even in the rather simple case of cubic direct-gap semiconductors like GaAs. Yet noticeable overall agreement for characteristic spectral features of the main absorption band, like van Hove singularities (including the main absorption edge, see below, and pre-band excitonic peaks, together with other many body effects) is often reached, sometimes with very good numerical estimates of optical band gap values from the fitted shape of the main absorption edge.
2.1. Transmission measurement of the absorption coefficient and reflection measurements of the complex index of refraction. Photoemission spectroscopy
A direct method to determine the absorption coefficient α and, thus, the imaginary part of χ, is to use equation (2.2) stating that the light transmitted through a crystal plate decreases exponentially with the thickness. Because the light penetration depth is 1/α, to measure a significant transmitted light intensity the sample thickness must be of the order of 1/α. For photon energies above the optical band gap, the absorption coefficient α increases abruptly with frequency, requiring several samples of decreasing thickness to explore a wide frequency range. To remedy this practical disadvantage, reflection measurements can be made instead. A linearly polarized monochromatic light beam hits the sample surface at a given incidence angle  , the polarization being either p or s with respect to the incidence plane defined by the incident wavevector and the surface normal. The intensity of the reflected light makes
, the polarization being either p or s with respect to the incidence plane defined by the incident wavevector and the surface normal. The intensity of the reflected light makes 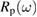 or
or 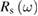 measurable, these functions of the complex refractive index
measurable, these functions of the complex refractive index  =
= 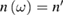 + i
+ i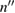 being given by the Fresnel formulae:
being given by the Fresnel formulae:
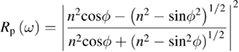
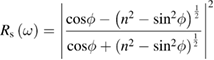
from which both  and
and  can be obtained as functions of frequency. Nowadays synchrotron radiation is used as source of the probe beam to cover a photon energy range between the infrared and the x-ray region with high intensity. The main drawback of reflection based techniques is their sensitivity to surface contamination even if UHV conditions are used. Spectroscopic ellipsometry (SE) is an alternative equivalent technique which will not be treated here being based on similar physical principles and with the same advantages and limitations. Even some emission spectroscopies, like photoluminescence, share such undesired sensitivity to surface defects. Still today the most popular method to measure the optical response is normal incidence reflection spectroscopy. It hinges on a generalization of equation (2.1). A complex normal reflectivity
can be obtained as functions of frequency. Nowadays synchrotron radiation is used as source of the probe beam to cover a photon energy range between the infrared and the x-ray region with high intensity. The main drawback of reflection based techniques is their sensitivity to surface contamination even if UHV conditions are used. Spectroscopic ellipsometry (SE) is an alternative equivalent technique which will not be treated here being based on similar physical principles and with the same advantages and limitations. Even some emission spectroscopies, like photoluminescence, share such undesired sensitivity to surface defects. Still today the most popular method to measure the optical response is normal incidence reflection spectroscopy. It hinges on a generalization of equation (2.1). A complex normal reflectivity

is formally introduced. Then it is shown that:
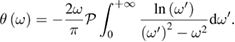
At this point, from the experimental measurement of 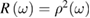 and using the above equations, the complex index of refraction and the complex electric susceptibility
and using the above equations, the complex index of refraction and the complex electric susceptibility 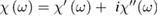 can be obtained. To introduce two other spectroscopic techniques which give access to the microscopic probabilities
can be obtained. To introduce two other spectroscopic techniques which give access to the microscopic probabilities  , it is worth anticipating, at least roughly, the dependence of probability rates on specific quantum processes responsible for the observed optical properties. Without assuming the translational invariance of crystals from the very beginning, it turns out that, for inter-band transitions involving only one photon and creating an electron–hole pair, with no phonon contribution (first order perturbation theory) [13]:
, it is worth anticipating, at least roughly, the dependence of probability rates on specific quantum processes responsible for the observed optical properties. Without assuming the translational invariance of crystals from the very beginning, it turns out that, for inter-band transitions involving only one photon and creating an electron–hole pair, with no phonon contribution (first order perturbation theory) [13]:
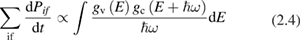
where 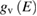 and
and 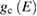 are the density of states of the valence and of the conduction band respectively. Equation (2.4) can be applied also to amorphous semiconductors. The energy dependence of the matrix elements of the perturbation operator has been neglected for it is generally weak. If we now introduce the total crystalline momentum conservation for the absorption process (crystals) the above equation can be written as (for a direct gap semiconductor) [14]:
are the density of states of the valence and of the conduction band respectively. Equation (2.4) can be applied also to amorphous semiconductors. The energy dependence of the matrix elements of the perturbation operator has been neglected for it is generally weak. If we now introduce the total crystalline momentum conservation for the absorption process (crystals) the above equation can be written as (for a direct gap semiconductor) [14]:
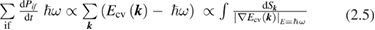
where  and the last surface integral is proportional to
and the last surface integral is proportional to 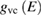 the joint density of states of the valence and the conduction bands, taking into account only allowed vertical transitions neglecting the photon momentum. In this way the main absorption band is dominated by van Hove singularities (discontinuities in
the joint density of states of the valence and the conduction bands, taking into account only allowed vertical transitions neglecting the photon momentum. In this way the main absorption band is dominated by van Hove singularities (discontinuities in 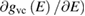 occurring whenever the denominator in the surface integral vanishes. The most import among them is around the optical band gap energy
occurring whenever the denominator in the surface integral vanishes. The most import among them is around the optical band gap energy 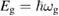 and determines, at least in the simplest cases, the shape of the main absorption edge. When phonons are involved (indirect gap semiconductors) at least second order perturbation theory must be applied. Moreover, if excitonic features are present in the experimental spectra, the theory must include also two bodies (or many-body) effects. Before discussing the difficulties connected with the experimental shape of the main absorption edge, it is convenient to introduce also photoemission spectroscopy. This spectroscopy is extremely powerful for the determination of the band structure of semiconductors even though the access to the density of states is even more indirect than in the previous cases and requires a lot of specific experimental skills. The sample surface is irradiated by rather high energy monochromatic photons and, as a result, charge carriers are injected in vacuum from the valence band and/or from core states of the solid. Then the energy distribution of the emitted electrons is analyzed as a function of photon energy
and determines, at least in the simplest cases, the shape of the main absorption edge. When phonons are involved (indirect gap semiconductors) at least second order perturbation theory must be applied. Moreover, if excitonic features are present in the experimental spectra, the theory must include also two bodies (or many-body) effects. Before discussing the difficulties connected with the experimental shape of the main absorption edge, it is convenient to introduce also photoemission spectroscopy. This spectroscopy is extremely powerful for the determination of the band structure of semiconductors even though the access to the density of states is even more indirect than in the previous cases and requires a lot of specific experimental skills. The sample surface is irradiated by rather high energy monochromatic photons and, as a result, charge carriers are injected in vacuum from the valence band and/or from core states of the solid. Then the energy distribution of the emitted electrons is analyzed as a function of photon energy  . In the same spirit as in equation (2.3) this energy distribution can be written: [13]
. In the same spirit as in equation (2.3) this energy distribution can be written: [13]
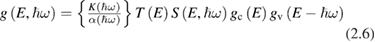
where K includes parameters of the experimental instrument,  is the absorption coefficient, T an escape probability factor and S is the fraction of excited electrons lost because of scattering. The main advantages with respect to absorption spectroscopy are: (a) the possibility of measuring absolute values of energy (e.g. the top of the valence band) and (b) a separate measurement of both
is the absorption coefficient, T an escape probability factor and S is the fraction of excited electrons lost because of scattering. The main advantages with respect to absorption spectroscopy are: (a) the possibility of measuring absolute values of energy (e.g. the top of the valence band) and (b) a separate measurement of both 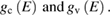
Anyhow a thorough analysis of excited states (conduction band) can only be obtained by inverse photoemission (IPES). Very recently angle-resolved photoelectron spectroscopy (ARPES) [11] has revealed to be crucial to put into evidence the role of strongly bound excitons in TiO2 anatase single crystals and nanoparticles and to elucidate the origin of crossover from polarons to Fermi liquids in transition metal oxides [15].
2.1.1. The determination of optical band gap Eg is theory laden.
Very often the goodness of ab initio computational methods of electronic structure of crystals is judged on the basis of their capability to reproduce the experimental value of optical band gap Eg. With this attitude, the intriguing experimental phenomenology underpinning the shape of the main absorption edge is given no enough attention. Only in the ideal case of a perfect direct gap semiconductor with no measurable excitonic peaks, the measurement of Eg is both unambiguous and straightforward. In this case, using equation (2.5) for  close to Eg:
close to Eg:
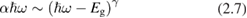
with γ = 1/2 for allowed transition (or γ = 3/2 for forbidden transitions) [10].
In indirect gap semiconductors phonons are either emitted or absorbed during photon absorption and
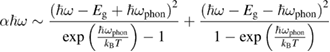
smoothing out the main absorption edge and introducing a strong temperature dependence [10].
At photon energies below Eg absorption can be due to inelastic scattering of exciton-polaritons from phonons [10] contributing with both a line and a continuous spectrum. This effect is well documented and has been known in GaAs [16] since 1962: it introduces a significant and structured temperature dependence in the increasing initial part of the absorption spectrum overshadowing the simple shape described by equation (2.7).
Yet some crystals (like, e.g. CdS, trigonal Se and TiO2 anatase) exhibit none among the above behaviors, showing instead an exponential increase of the absorption coefficient as
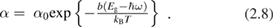
Where b is a constant and T is the temperature down to a characteristic value 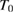 and, below,
and, below,  itself. In amorphous semiconductors, this is the so called Urbach edge, to be expected from the mainly localized nature of electron wavefunctions. In crystals, mainly characterized by extended and travelling Bloch states, this shape of the absorpion edge is not completely understood though three different explanations have been proposed: [13] (a) bound excitons interactions with phonons [17] (see figure 1); (b) electric field broadening of absorption edge; (c) electric field broadening of an exciton line.
itself. In amorphous semiconductors, this is the so called Urbach edge, to be expected from the mainly localized nature of electron wavefunctions. In crystals, mainly characterized by extended and travelling Bloch states, this shape of the absorpion edge is not completely understood though three different explanations have been proposed: [13] (a) bound excitons interactions with phonons [17] (see figure 1); (b) electric field broadening of absorption edge; (c) electric field broadening of an exciton line.
Figure 1. Optical spectra of anatase TiO2 single crystals, showing the effect of bound excitons on the shape and position of the absorption edge. Imaginary part of the dielectric function at 20 K with the electric field polarised along (a) the a-axis (E ⊥ c) and (b) the c-axis (E ǁ c) of the anatase primitive cell. The experimental data measured by spectroscopic ellipsometry on a pristine (n ~ 0 cm−3) anatase TiO2 single crystal are reported in blue, while those obtained on a highly n-doped single crystal (n = 2 × 1019 cm−3) in red. The quasiparticle indirect gap Eind = 3.47 eV and direct gap Edir = 3.97 eV, as estimated by ARPES, are indicated by dashed grey and black vertical lines, respectively. Reproduced from [11]. CC BY 4.0.
Download figure:
Standard image High-resolution image2.2. Scanning tunneling spectroscopy (STS)
All spectroscopic techniques described above furnish a spatially averaged information over a surface region whose least size is of the order of photon wavelength. Scanning tunneling microscopes can be used to get an information similar to that of photoemission but with a much higher space resolution, down to atomic resolution at very low temperatures. For spectroscopic use the tip of the microscope (with an apex radius of curvature rt) is positioned just above a fixed point of the surface and at a fixed distance z from it. Then the polarization voltage V is varied, tipically from −3 V to +3 V (or less). Correspondingly the tunneling current I between the tip and the surface (or viceversa) is measured. Using the simplest possible model [18], I can be written as:
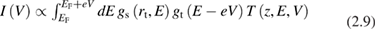
where EF is the Fermi energy, gs is the local density of states of the sample, gt is the local density of states of the tip
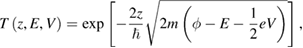
is the transmission probability of a trapezoidal vacuum barrier, 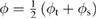 the work function average of the two electrodes and
the work function average of the two electrodes and 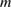 the electron mass. Provided
the electron mass. Provided 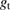 and
and 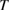 are known,
are known, 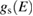 can be evaluated around the Fermi energy, measuring
can be evaluated around the Fermi energy, measuring 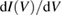 by means of the built-in lock-in technique. The error made by this procedure and more realistic interpretative equations than (2.9) are discussed in [19] and references therein. For geometric instrumental reasons
by means of the built-in lock-in technique. The error made by this procedure and more realistic interpretative equations than (2.9) are discussed in [19] and references therein. For geometric instrumental reasons 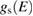 is more properly an almost normal projection of the local density of states and contains surface features. STS has the great advantage of being capable of measuring both occupied and empty states just changing the sign of the polarization potential V. A critical issue remains the mixing with the density of states of the tip [19].
is more properly an almost normal projection of the local density of states and contains surface features. STS has the great advantage of being capable of measuring both occupied and empty states just changing the sign of the polarization potential V. A critical issue remains the mixing with the density of states of the tip [19].
3. Many-body calculations of electronic structure of oxides
3.1. Introduction
As already mentioned in section 2, a quantitative understanding of the electronic excitations in materials and how they lead to the measured optical gaps and energy band dispersion in angle-resolved photoemission and inverse photoemission spectra (ARPES and IPES) must be based on appropriate theoretical models. Depending on the type of experiment, involving neutral or charged excitations, different theoretical tools may be needed. Charged excitation energies as those measured in ARPES and IPES, but also in STM, are by definition poles of the system's one-particle (electron or hole) Green's function G. The latter describes the probability amplitude for transitions of an electron or a hole from the initial to the final state throughout the fully interacting many-electron system. On the other hand, neutral excitations probed by optical techniques, such as SE or reflectivity, are intrinsically described by the macroscopic dielectric function of the system, whose knowledge requires to go beyond the single quasiparticle concept. This may be achieved, e.g. by introducing electron–hole (two particles) Green's functions [20] which may be computed within the formalism of the Bethe-Salpeter equation.
The knowledge of band structure (quasiparticle) gaps between valence and conduction single-particle states may however give a realistic estimate of the optical gaps if the electron–hole interactions (i.e. excitonic effects) are small enough to be neglected. As recently exemplified by Baldini et al [11] in the case of TiO2, this is not a trivial issue, and the key for substantially advancing our physical understanding is often found by the use of more than one experimental techniques, in combination with suitable ab initio theoretical simulations [11].
In any case, the calculation of quantitatively correct quasiparticle dispersion bands is an essential ingredient. Besides optical properties, a quantitative knowledge of the one-particle band structure is also of paramount importance when electron transport properties are considered, e.g. in non-homogeneous devices such as in solar cells, or in systems for electrochemical applications, where band alignment properties determine the functionality of the system.
The remaining of this section will be devoted to the Hedin's GW method [21–23], the state-of-the-art approach to include many-body effects in ab initio band structure calculations, focusing on its application to oxide materials.
3.2. The GW approach
The GW method has become the state-of-the-art approach for ab initio electronic structure calculations of materials based on many-body perturbation theory [24]. In the quasiparticle picture describing charged electronic excitations, the single particle energies and wavefunctions are solution of the quasiparticle equation,
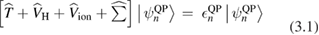
whose structure is mathematically similar to the one of the DFT Kohn–Sham equations [25],
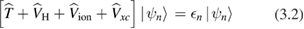
with the fundamental difference that the exchange-correlation potential 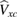 is replaced by a nonlocal, energy dependent generalized potential
is replaced by a nonlocal, energy dependent generalized potential 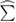 known as the electronic self-energy, describing the quantum mechanical exchange and correlation effects on the quasiparticle spectrum. The common contributions in equations (3.1) and (3.2) represent the electronic kinetic energy (
known as the electronic self-energy, describing the quantum mechanical exchange and correlation effects on the quasiparticle spectrum. The common contributions in equations (3.1) and (3.2) represent the electronic kinetic energy (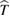 ), the classical Hartree potential (
), the classical Hartree potential (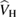 ), and the ionic potential (
), and the ionic potential ( ). Here n is a label identifying the electronic state; in the case of a Bloch wavefunction, it represents the band index, the wavevector in the first Brillouin zone, and the spin polarization.
). Here n is a label identifying the electronic state; in the case of a Bloch wavefunction, it represents the band index, the wavevector in the first Brillouin zone, and the spin polarization.
Within Hedin's self-consistent scheme, one could in principle construct systematically improved approximations to the self-energy. Moreover, one could build further approximations to include electron–hole interaction effects [26] and thus calculate optical absorption spectra and related quantities. We address the reader to existing reviews on how, starting from the Hedin's scheme, the electron–hole interaction can be also taken into account by further extending Hedin's ideas, within the same ab-initio framework [20].
3.2.1. The G0W0 approximation.
In principle, one should evaluate the self-energy by solving self-consistently the set of Hedin's equations, as graphically represented in figure 2; besides the self-energy Σ the fundamental quantities defined in Hedin's scheme are the one-particle Green's function G, the polarizability 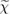 , the screened Coulomb interaction W, and the vertex function Γ. The latter quantity describes the interaction between electrons and holes, which may be created in the system upon, e.g. light absorption (neutral excitation).
, the screened Coulomb interaction W, and the vertex function Γ. The latter quantity describes the interaction between electrons and holes, which may be created in the system upon, e.g. light absorption (neutral excitation).
Figure 2. Schematic representation of the iterative solution of the Hedin's equations (specified on the sides of the pentagon), which link the self-energy Σ the one-particle Green's function G, the vertex function Γ, the irreducible polarizability 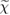 , and the screened Coulomb interaction W. Reprinted from [27], Copyright 2009, with permission from Elsevier.
, and the screened Coulomb interaction W. Reprinted from [27], Copyright 2009, with permission from Elsevier.
Download figure:
Standard image High-resolution imageThe GW approximation is meant to describe charged excitations; hence, the electron–hole interaction is neglected, and the vertex function is assumed to be 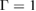 . Within this approximation for
. Within this approximation for 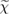 , the self-energy can thus be formally written as (see the top-left side of the pentagon in figure 2)
, the self-energy can thus be formally written as (see the top-left side of the pentagon in figure 2)

where the screened Coulomb interaction is obtained from the polarizability (density–density linear response function) within the random phase approximation,

(base of the pentagon in figure 2) which also assumes that electrons and holes do not interact.
In principle, equations (3.3) and (3.4) should be evaluated at self-consistency within the Hedin's scheme (even when neglecting the vertex), i.e. G and 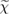 should be expressed in terms of the self-consistent quasiparticle energies and wavefunctions. In practice, this approach is computationally very expensive even for relatively small systems; a more common approach consists in evaluating the one particle Green's function by using the electronic eigenvalues and wave functions computed for some reference non-interacting system, typically the DFT Kohn–Sham system. The non-interacting Green's function G0, evaluated for the reference Kohn–Sham system, reads
should be expressed in terms of the self-consistent quasiparticle energies and wavefunctions. In practice, this approach is computationally very expensive even for relatively small systems; a more common approach consists in evaluating the one particle Green's function by using the electronic eigenvalues and wave functions computed for some reference non-interacting system, typically the DFT Kohn–Sham system. The non-interacting Green's function G0, evaluated for the reference Kohn–Sham system, reads
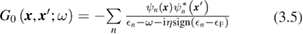
where 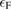 denotes the Fermi energy, and
denotes the Fermi energy, and 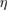 is an arbitrarily small constant which modifies the form of the Green's function so as to describe the propagation of an additional electron (for
is an arbitrarily small constant which modifies the form of the Green's function so as to describe the propagation of an additional electron (for 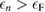 ) or hole (for
) or hole (for 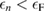 ) in the system. The spatial and spin coordinates are denoted by x, and ω indicates the frequency of the density perturbation. Within the independent particle approximation, the electronic polarizability
) in the system. The spatial and spin coordinates are denoted by x, and ω indicates the frequency of the density perturbation. Within the independent particle approximation, the electronic polarizability 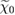 is given by the product of the non-interacting electron and hole Green's functions, as obtained from equation (3.4) by approximating G with G0 as given by (3.5). In this approximation, the screened Coulomb interaction W0 is obtained by solving the corresponding Dyson-like equation connecting
is given by the product of the non-interacting electron and hole Green's functions, as obtained from equation (3.4) by approximating G with G0 as given by (3.5). In this approximation, the screened Coulomb interaction W0 is obtained by solving the corresponding Dyson-like equation connecting 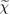 and W, as shown in figure 2. The self-energy is thus expressed in the non-self-consistent G0W0 approximation, and the quasiparticle energies are computed from first-order perturbation theory on top of the Kohn–Sham eigenvalues and wavefunctions:
and W, as shown in figure 2. The self-energy is thus expressed in the non-self-consistent G0W0 approximation, and the quasiparticle energies are computed from first-order perturbation theory on top of the Kohn–Sham eigenvalues and wavefunctions:
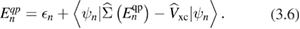
The implicit equation (3.6) may be solved by linearizing the self-energy (which should be in principle evaluated at the quasiparticle energy 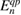 ) around the corresponding Kohn–Sham eigenvalue
) around the corresponding Kohn–Sham eigenvalue 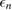 , or by obtaining the solution recursively, using e.g. the secant method. The DFT eigenvalues and wavefunctions are typically computed within the local density approximation (LDA) or the generalized gradient approximation (GGA). While this approach normally gives accurate band structures for sp semiconductors, it may fail for materials exhibiting spatially localized electronic states close to the Fermi energy, such as correlated transition metal oxides. In this case, one has to adopt a different DFT starting point, such as those obtained within DFT + U or hybrid DFT, or alternatively define an optimal starting point which avoids such arbitrary choices (see section 3.5 below).
, or by obtaining the solution recursively, using e.g. the secant method. The DFT eigenvalues and wavefunctions are typically computed within the local density approximation (LDA) or the generalized gradient approximation (GGA). While this approach normally gives accurate band structures for sp semiconductors, it may fail for materials exhibiting spatially localized electronic states close to the Fermi energy, such as correlated transition metal oxides. In this case, one has to adopt a different DFT starting point, such as those obtained within DFT + U or hybrid DFT, or alternatively define an optimal starting point which avoids such arbitrary choices (see section 3.5 below).
3.2.2. The COHSEX approximation.
One may introduce a further simplification to the RPA screened Coulomb interaction W, which can be conveniently expressed in real space as

where 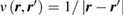 is the bare Coulomb potential, and Wp denotes the polarizable part of the W, which is a frequency dependent quantity describing electronic screening. As originally suggested by Hedin, [21] Wp may be approximated by taking its static limit (
is the bare Coulomb potential, and Wp denotes the polarizable part of the W, which is a frequency dependent quantity describing electronic screening. As originally suggested by Hedin, [21] Wp may be approximated by taking its static limit ( ), obtaining a frequency independent self-energy (the COHSEX self-energy), [23] which can be seen as originating from two contributions: a Coulomb hole (COH) self-energy, describing the electrostatic interaction between an electron and its Coulomb hole arising from static polarization of the system; a screened exchange (SEX) self-energy, describing the statically screened Fock exchange interaction, proportional to the inverse of the macroscopic dielectric constant of the system. The COHSEX approach goes beyond the Hartree–Fock theory, taking into account electronic screening, although only on a macroscopic scale and neglecting dynamical effects. The lack of frequency dependence suggests that a connection may be established between the COHSEX self-energy and the DFT exchange-correlation potential, provided that the latter includes in some form the nonlocal Fock exchange, as in hybrid functionals. This relationship allows one to define dielectric-dependent hybrid functionals, as discussed in section 4.2 below.
), obtaining a frequency independent self-energy (the COHSEX self-energy), [23] which can be seen as originating from two contributions: a Coulomb hole (COH) self-energy, describing the electrostatic interaction between an electron and its Coulomb hole arising from static polarization of the system; a screened exchange (SEX) self-energy, describing the statically screened Fock exchange interaction, proportional to the inverse of the macroscopic dielectric constant of the system. The COHSEX approach goes beyond the Hartree–Fock theory, taking into account electronic screening, although only on a macroscopic scale and neglecting dynamical effects. The lack of frequency dependence suggests that a connection may be established between the COHSEX self-energy and the DFT exchange-correlation potential, provided that the latter includes in some form the nonlocal Fock exchange, as in hybrid functionals. This relationship allows one to define dielectric-dependent hybrid functionals, as discussed in section 4.2 below.
3.3. Early applications of the GW methods to oxide materials
Despite the fact that the GW idea was initially introduced in the sixties, the lack of computational resources suitable to work out numerical solutions has limited its application to very simple model systems, such as the homogeneous electron gas, where analytical predictions could be made [28, 29]. Only in the eighties the GW method started to be applied to real materials, taking into account their microscopic structure at the atomistic level [30–34]. Due to the additional complexity of oxide materials with respect to elemental semiconductors such as silicon, applications of GW to oxides started to appear only a decade later, with the works by Massidda et al on MnO [35], NiO [36], and VO2 [37]. Such works employed a simplified scheme, neglecting dynamical effects in the self-energy (i.e. the energy dependence of Σ), with good results for theoretical bandgaps compared to experiment. Another early application of GW to oxides is described in the work by Králik and coworkers for the case of ZrO2 [38].
Some GW results on bulk oxides (namely In2O3 and MnO) can be found in the review by Bechstedt et al [39].
3.4. One-shot GW calculations: applications to d0 oxides
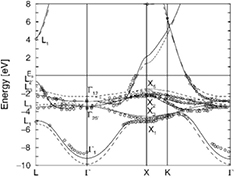
The large majority of today's GW band structure calculations are based on the so-called 'one-shot' approach (see section 3.2.1), where no self-consistency between G, W and Σ is enforced. In other words, G and W are only computed once, starting from initial DFT band structure results, and the band energy correction is obtained by evaluating (Σ − Vxc) perturbatively on the LDA or GGA Kohn–Sham eigenstates. The G0W0 approach is generally quite successful in the case of d0 oxides, with results for the computed band gaps which are essentially of the same quality as in the case of simple sp semiconductors. Noticeably, (Σ − Vxc) has been shown to introduce nontrivial (state-dependent) shifts of the d bands with respect to sp ones in noble metals, leading to band structure results in much better agreement with the experimental ARPES data than at the LDA/GGA level, as demonstrated in the case of copper shown in figure 3 [40]. Oxide materials whose band structure turns out to be well described at the G0W0 level include MgO [41] and TiO2 [42, 43]. For the latter material, calculations also reproduce the effects of strain [44] and that of Nb impurities [45]. More recently, also the case of bulk WO3 has been shown to be well described at the G0W0 level, starting from LDA or PBE [46, 47].
Figure 3. GW results for the bulk copper band structure, compared with the DFT-LDA results (dashed line), and with the experimental data reported in [49] (circles). Reprinted figure with permission from [40], Copyright 2002 by the American Physical Society.
Download figure:
Standard image High-resolution imageIn the high-throughput ab initio study by Hautier et al [48], where more than 4000 binary and ternary oxide compounds have been scanned in order to identify those with the lowest electron effective mass, G0W0 results have been taken as a reference when experimental data were not available.
Although G0W0 is reported to work well in many cases, some exceptions within simple oxides exist. The most famous one is that of ZnO, which has been reported in the past as a problematic case for GW: different theoretical works gave widely scattered results concerning a simple number as its direct bandgap at the zone center (see table 1). In ZnO, the top valence and bottom conduction states have a very different character, as shown by several authors [50, 51], and require large basis sets to be correctly described. Moreover, using plasmon pole models for the frequency integrations in GW may be a delicate choice, especially when semicore electrons are included in the valence within a pseudopotential scheme. This has been clearly shown by Stankovski et al [52], who demonstrated that the previous work by Louie and coworkers [53], using the Hybertsen plasmon pole model [33] based on sum rules, was affected by a miscount of the number of active electrons. The picture has hence been clarified by disentangling effects due to convergence issues and the plasmon pole approximation for the dynamical screening [54]. The influence of plasmon pole models in G0W0 calculations for oxide materials has been investigated by Samsonidze et al [55] for ZnO, TiO2, and Co2O and by Laasner [56] in the case of CdWO4.
Table 1. Band gap of ZnO (eV) computed within GW at various levels of theory and using different numerical approximations for the treatment of the frequency dependence in the self-energy (FF: full-frequency integration; PPM: plasmon pole models), the exchange-correlation functional used in the starting DFT calculation, and the treatment of the electron-ion interaction (AE: all-electron; NCPP: norm-conserving pseudopotentials; PAW: projected augmented wave method). G0W0 denotes one-shot GW, GW0 includes self-consistency only in the Green's function, and GW is fully self-consistent GW. Results from quasiparticle self-consistent GW (QPscGW) are also reported, in which the vertex correction has been approximately evaluated (QPscGW + fxc). The experimental band gap is 3.44 eV [78].
| GW level | DFT level | Band gap |
|---|---|---|
| G0W0 (FF) | PBE (PAW) | 2.12 |
| GW0 (FF) | PBE (PAW) | 2.54 |
| GW (FF) | PBE (PAW) | 3.20 |
| G0W0 (PPM) | LDA+U (NCPP) | 3.6 |
| G0W0 (FF) | LDA (NCPP) | 2.4 |
| G0W0 (FF) | LDA (AE) | 2.83 |
| G0W0 (FF) | PBE0 | 3.32 |
| G0W0 (PPM) | PBE (NCPP) | 3.06 |
| QPscGW | PBE (NCPP) | 4.61 |
| QPscGW + fxc | PBE (NCPP) | 3.42 |
aBruneval et al [62]. bStankovski et al [52]. cGerosa et al [51]. dCourths and Hüfner [49]. eChen and Pasquarello [79]. fFriedrich et al [50]. gGrüneis et al [91].
However, there are systems where the reported mismatch between computed G0W0 band structure and experimental photoemission data cannot be explained in terms of technicalities such as basis set convergence issues, the use of pseudopotentials, or simplifications in the description of the dynamical screening. Systems such as VO2, where G0W0 breaks down completely [57] are a clear indication that the intrinsic approximations of the method should be overcome to achieve a correct physical description of some among the oxide materials.
3.5. Beyond G0W0@LDA/GGA: self-consistency in GW
A first reason why G0W0 may fail in some oxide materials is linked to the lack of self-consistency, i.e. to the fact that the starting LDA or GGA wavefunctions are kept unchanged. Prototypical cases are systems which appear to be metallic (gapless) at the starting LDA/GGA level, while they are experimentally semiconductors or insulators. In such cases, G0W0 may be unable to open a gap, and the LDA/GGA Kohn–Sham wavefunctions exhibit wrong spatial localization properties.
This problem is usually negligible in d0 oxides, where d states are only slightly affected by the LDA/GGA overdelocalization problem, but may become important in systems such as NiO or CoO. In general, G0W0 results may be affected by the choice of the starting point, as shown by Bechstedt and coworkers in 2007 [58], and more recently by Kang et al for the case of post transition metal oxides such as Ga2O3, In2O3, and SnO2 [59]. An obvious solution for the starting point dependence would be to iterate the Hedin equations (see figure 2) to self-consistency. However, a fully self-consistent GW approach has been shown to fail if vertex corrections are not considered at the same time (i.e. self-consistency should be enforced on the full pentagon, including the nontrivial vertex function Γ in figure 2, leading to the so-called GWΓ approach) [60]. Self-consistency within GW has been shown to worsen G0W0 results for many systems [61]: essentially, a cancellation of errors has been shown to occur in the one-shot approach [62]. Since a fully self-consistent GWΓ approach is far beyond the present computational capabilities, even for very simple systems such as bulk silicon, alternative approaches allowing one to get rid of a possibly 'too wrong' starting point wavefunction are necessary. For this reason, several ideas have been proposed in the GW community, ranging from a GW0 scheme (where only G is updated), tested in the cases of ZrO2 and HfO2 [63], to strategies to choose an optimal starting point to be used in a one-shot G0W0 scheme. The latter idea has indeed been implemented in several flavors: (i) starting from an LDA+U calculation, with applications to lanthanide oxides [64, 65], MnO, FeO, CoO, NiO [66], and NiO, MnO, V2O3 [67]; (ii) starting from a COHSEX calculation, tested on TCOs (transparent conducting oxides) [68]; (iii) starting from hybrid functional calculations (typically HSE), as investigated in the case of MgO; [58] MnO, FeO, CoO, InO [69]; NiO [70]; and SnO2 [71]; and (iv) starting from LDA-1/2, tested in the case of MgO and ZnO [72].
A further step along the path of the 'starting point problem' has been taken with the so-called quasiparticle self-consistent GW (QPscGW) approach [73], introduced by van Schilfgaarde and coworkers in 2004 [74, 75] and recently applied to several oxide materials ranging from MnO, CoO, TiO [76], to TiO2 and cubic SrTiO3 [77].
In the QPscGW scheme self-consistency is introduced at the G0 level, i.e. one seeks an optimal non-interacting Green's function, having poles already at the right energy position, as the best starting point for a subsequent one-shot GW calculation. In this way, even a critical system such as VO2, where G0W0 breaks down completely also when an improved (hybrid functional) starting point is chosen [80], turns out to be well described. In most cases where G0W0 fails, QPscGW may be considered as a way for a systematic improvement of band structure theoretical results of oxide materials.
3.6. Beyond GW
Although QPscGW may represent an optimal choice as a starting point, in the intriguing case of copper oxide (CuO) it has been shown to fail [81]. The computed gap turns out to be larger than 4 eV, against an experimental gap of 1.7 eV: the reason for this disagreement has been traced back to a substantial underestimation of the dielectric screening entering in W [82]. On the other hand, in the case of CuO some authors have also used ad hoc corrections [83, 84], at the expense of losing the generality expected in a fully ab initio scheme. Possible sources of remaining errors in QPscGW are the neglect of three-points vertex contributions (which would require a GWΓ approach as discussed by van Schilfgaarde himself) and the neglect of lattice polarization effects and the electron–phonon interaction, as thoroughly discussed in a recent review by Giustino [85]. The effect of the lattice polarization has been considered for different systems, including oxides such and V2O5 (having an experimental bandgap almost coinciding with the LDA one [86]), and MgO [87]. Excitonic effects are known to play an important role in the case of CuO2 [81].
Further developments aimed to go beyond the GW approximation have been proposed also in the case of SrVO3, where the effects of dynamical vertex corrections has been studied within a GW + C scheme based on an exponential expansion of G [88]. The same oxide has been considered in the perspective of merging GW with dynamical mean field theory (DMFT) [89]. The role of vertex corrections in GW band structure calculations for oxide materials has been studied also in the case of BaBiO3 [90], CdO [91], TiO2, ZnO and MgO [92]. In general, the problem of external vertex corrections (i.e. how to implement a GWΓ scheme), as well as the problem of finding the best way to compute W (where 'internal' vertex corrections may influence the screening) are presently still open questions in the GW community.
3.7. GW Applications to realistic oxide surfaces and interfaces
GW has been successfully applied to study semiconductor surfaces since more than 15 years (see e.g. [93, 94, 95]). However, oxide surfaces still represent a challenge, because the many degrees of freedom (large number of atoms/ big supercells), associated with the complexity of many body effects in the bulk band structure, as described in the previous subsections, make actual calculations exceedingly heavy from the computational point of view. This is the reason why, till very recently, only simplified GW approaches were possible for oxide surfaces (see e.g. [96]).
However, it is precisely in the presence of a surface or an interface that the ability to compute the absolute position of electronic energy levels becomes important: for example, applications based on electron transport, as in the case of solar cells require an accurate knowledge of band edge alignment. The same is true in the case of effective 2D oxide systems and their interplay with adsorbates [97].
Thanks to the development of efficient methods to compute the screened interaction W avoiding extensive summations over empty states (see e.g. [98]), and to the availability of more powerful computational resources, large scale full GW calculations suitable to study oxide surfaces and interrfaces are now becoming a reality [99, 100]. The feasibility of ab initio GW calculations for real surfaces was clearly demonstrated in the work by Govoni and Galli [101] and that by Gao et al [102]. As a consequence, GW calculations of surfaces and complex interfaces [103], including those of transition metal oxides of interest for photoelectrochemical water splitting [104] (see figure 4) have recently started to appear in the literature. The field has been recently reviewed by Pham et al [8].
Figure 4. Band edge alignment, obtained at the G0W0 level, at the photoanode/catalyst WO3/IrO2 interface for the oxygen evolution reaction. The effect of water on the band alignment was taken into account by using continuum solvation models. The relative position of the conduction band minimum of WO3 (ECBM) and the Fermi level (Ef) of the interface, in the absence of water (left panel), and in the presence of water in contact with the absorber and the catalyst at the same time (right panel) are shown. Reprinted with permission from [104]. Copyright 2015 American Chemical Society.
Download figure:
Standard image High-resolution image4. Recent developments in hybrid functional calculations of materials
4.1. Hybrid functionals: motivations, development and application to electronic structure calculations
Although many body GW based methods have become increasingly popular even for electronic structure calculations of large condensed systems including hundreds of atoms, especially thanks to recent methodological and algorithmic developments, hybrid functionals represent a computationally more affordable alternative and a practical way to fix some of the issues of local and semilocal density functionals. Moreover, in some pathological systems, in which e.g. the self-interaction error is particularly critical, reproducing the correct ground state within DFT, including the spatial localization of relevant electronic states, is a fundamental prerequisite to obtaining accurate quasiparticle corrections, and therefore band structures properly including many body effects (see section 3.5).
Two, related, major drawbacks of local and generalized gradient exchange-correlation approximations are the incomplete cancellation of the density self-interaction potential included in the Hartree term, and the absence of a derivative discontinuity in the total energy functional with respect to density. They result, for example, in a qualitatively wrong description of charge transfer and dissociation mechanisms in molecular systems [105]. With regard to spectroscopic properties, the ionization potential (IP) and electron affinity (EA) of a finite system can be rigorously calculated using the ΔSCF approach [106]; in this case the lack of a derivative discontinuity manifests in an inaccurate prediction of the IP and EA, which may be cured by using orbital dependent energy functionals [107]. For the same reasons, the Kohn–Sham approach in which local and semilocal functionals are naturally defined provides band gap values for solids which are too small compared to experiments; this issue has a fundamental origin in the inability of the Kohn–Sham gap in capturing the derivative discontinuity, independently of the specific functional used, but for extended systems it cannot be easily circumvented using the ΔSCF method [108]. However, a practical solution to the band gap problem is again offered by orbital-dependent functionals, which are well defined in a generalized Kohn–Sham (GKS) scheme [109]. Band gaps computed within the GKS framework turn out to be in better agreement with experiments [110], since a portion of the exchange-correlation derivative discontinuity is already incorporated in the calculated GKS gap [108].
Hybrid exchange-correlation functionals are a popular implementation of orbital-dependent functionals, whose most common one-parameter form (defining full-range functionals, parametrized by the exchange fraction α) can be justified on the basis of the adiabatic connection theorem [111]; their introduction in quantum chemistry originates from the need of improving the prediction of various molecular thermochemical properties, including e.g. atomization energies [112, 113].
Hybrid functionals are constructed by admixing a portion of the exact exchange (EXX) energy 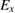 to GGA type functionals (whose exchange and correlation contributions are denoted
to GGA type functionals (whose exchange and correlation contributions are denoted  and
and 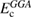 , respectively); the general form of the exchange-correlation energy for one-parameter hybrid functionals reads
, respectively); the general form of the exchange-correlation energy for one-parameter hybrid functionals reads
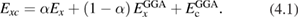
The EXX energy is defined in analogy with the exchange energy of Hartree–Fock theory, and the fraction of EXX, denoted α in the case of one-parameter hybrids, may vary from 0 (in which case the original GGA functional is obtained) to 1 (Kohn–Sham exact exchange potential) [114]; at variance with Hartree–Fock, however, the EXX integral in hybrids is evaluated using the GKS DFT wavefunctions. Several hybrid functionals have been designed, which differ by the specific choice of the GGA functional approximating the semilocal part, and the value set for the exchange fraction. The scope of the present discussion is limited to those functionals which have seen wider application to solids and solid state chemical systems, while for an overview of other approaches, including e.g. local hybrids and functionals involving unoccupied orbitals and eigenvalues, the reader is referred to [115]. The PBE0 [116] and B3LYP [117] functionals are widely employed in solid state applications. B3LYP does not follow equation (4.1), but is based on a different three-parameter functional form fitted to reproduce experimental data sets for molecules, and incorporating 20 percent of exact exchange (equivalent to α = 0.20). PBE0 instead builds on the original Becke's one-parameter hybrid (equation (4.1)), using α = 0.25. A formal justification for this value of α was provided on the basis of comparison with many-body perturbation theory [118]; however, the validity of this argument is strictly limited to reproduction of atomization energies of molecular data sets.
Hybrid functionals designed for quantum chemical calculations saw their first applications to solids at the beginning of the 2000s, providing a significant improvement over GGA in the prediction of band gaps, and a comparable or better performance for structural and cohesive properties of semiconductors [119–121]. Remarkably, they were also proven able to adequately describe correlated rare earth and transition metal monoxides [122–125]; in fact, for these Mott-Hubbard insulators, which local and semilocal functionals typically predict to be metallic, the self-interaction error overdelocalizes the partially filled d orbitals, favoring a nonmagnetic ground state. The portion of exact exchange present in hybrids partially corrects the self-interaction error, yielding a qualitatively correct insulating ground state.
Shortly afterwards, hybrid functionals specifically tailored to condensed systems began to be developed. Based on one-parameter functional forms analogous to PBE0, range-separated hybrids were proposed and have since become increasingly popular in solid state calculations; they were designed so that the Coulomb kernel in the EXX energy is separated in short- and long-range contributions, which may then be treated independently. In particular, two different exchange fractions, pertaining to the short- and long-range part of the range-separated EXX energy, need to be specified. Two popular range-separated hybrids in which the long-range part of the Coulomb interaction is completely neglected (short-range hybrids) are the Heyd–Scuseria–Ernzerhof (HSE) [126, 127], and the screened exchange LDA (sx-LDA) [108, 128, 129], functionals, for which the short-range exchange fraction is set to 0.25 and 1, respectively. In HSE, the screened Coulomb interaction in EXX is defined through the complementary error function, 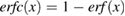 ,
,

where the screening parameter is fixed at an optimal value of ω = 0.106 a.u.−1 [130], independently of the system. Instead for sx-LDA, the screening function is defined to be system dependent. Screened exchange functionals were successfully applied to calculation of lattice constants, bulk moduli, and band gaps of solids [131–133], including correlated oxides [134], as well to defects in oxide materials [135]. HSE is today perhaps the most widely used hybrid functional for solid state calculations.
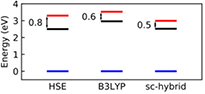
The considerable progress made in the development of efficient representations of the EXX operator [136–139], and its evaluation using highly scalable algorithms, have contributed to make hybrid functional calculations affordable for large scale condensed matter problems, including e.g. molecular dynamics simulations of aqueous solutions [140] and semiconductor-liquid interfaces [141]. However, the application of hybrid functionals originally designed for molecular quantum chemistry calculations, although often proving practically successful, is not theoretically well justified in condensed systems. One issue is related to the choice of the exchange-correlation approximation for the local part of the functional. For example, the widely used B3LYP functional does not fulfil the homogenous electron gas limit at slowly varying densities, since the Lee–Yang–Parr (LYP) correlation functional [142] is not correct in this limit. As a consequence, B3LYP does not accurately predict ground state properties (e.g. atomization energies) of solids with spatially delocalized electrons (metals and small gap semiconductors); if instead of LYP, the PW91 correlation energy is used, the resulting B3PW91 functional [112] possesses the correct free-electron gas limiting behavior, and an overall better performance is achieved in solid state calculations [143]. Nonetheless, both B3LYP and B3PW91 are semiempirical functionals optimized for molecular properties, and hence their application to condensed systems is questionable. However, even for functionals that are fundamentally better suited for solids (e.g. PBE0 and, especially, HSE), the choice of the correct value for the EXX fraction α remains an issue, which is even more critical for the calculation of spectroscopic properties. In fact, the value of α has a dramatic effect on the band structure and, in particular, on the computed band gap of semiconductors and insulators, which is systematically underestimated within GGA. For example, PBE0 overestimates by more than 50% the gap of simple semiconductors such as silicon and germanium, and tends to overestimate, although less seriously, the one of III–V semiconductors like GaAs and AlAs, while providing results in good agreement with experiment for more ionic compounds, such as AlN. At the opposite limit, strongly ionic insulators such as I–VII and II–VI compounds, including alkaline earth oxides (AeO, Ae = Be, Mg, Ca, Sr, Ba), exhibit large band gaps in the range 5–10 eV [144], reaching 14 eV in the case of LiF; for these materials, PBE0 underestimates the band gap by typically 15 to 20 percent [40]. The screened exchange HSE functional gives systematically smaller band gaps than PBE0, due to the cutoff introduced in the long-range tail of the Coulomb potential, resulting in the neglect of a portion of the exchange energy with respect to PBE0. Consequently, band gaps computed for many semiconductors with small to moderate gaps (including, e.g. III–V semiconductors and d0 metal oxides) turn out to be in better agreement with experiment [40, 50].
From the previous discussion, it is clear that a fixed value of α (e.g. 0.25 for PBE0) does not ensure equally accurate prediction of electronic properties when applied to a very broad variety of systems, such as metal oxides and strongly ionic materials. Instead, it is convenient to consider the EXX fraction as a system dependent parameter which may be affected by the bonding characteristics and, consequently, the electronic and dielectric properties of the material.
4.2. Dielectric-dependent hybrid functionals for bulk systems
The EXX fraction has been shown to be related to the strength of the electronic screening in the material. Early attempts at the construction of approximate (static) self-energies within the many-body GW scheme have shown that quasiparticle corrections to DFT eigenvalues are inversely proportional to the static dielectric constant of the material [145, 146]. Based on this observation, and invoking a formal analogy between the GKS exchange-correlation potential for full-range hybrids (obtained by deriving the total energy functional in equation (4.1) with respect to density) and the electronic self-energy in the COHSEX approximation (section 3.2.2), the EXX fraction was shown to be given as the inverse of the static dielectric constant [147–149]. Hence, for full-range dielectric-dependent hybrids the exchange-correlation potential takes a functional form analogous to PBE0 (equation (4.1)), but with a system dependent exchange fraction

which may be evaluated at different levels of accuracy, depending on the approximations made in computing the dielectric constant 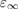 . Early works evaluated the dielectric constant using the Fermi's golden rule (independent particle approximation) [150] or the random phase approximation [151], or alternatively including the exchange-correlation contribution (local field effects) at GGA level [38]. Model dielectric functions have been used as well [146]. Inclusion of exchange-correlation effects beyond semilocal DFT was pursued in the works of Conesa [152] and Skone et al [153]. The nonlocal contributions to the dielectric response were fully taken into account by explicitly computing perturbed GKS orbitals in a self-consistent way, by means of the coupled-perturbed Kohn–Sham method [154]. The computed dielectric constants turned out to be in much better agreement with experiment compared to the values obtained neglecting local field effects or treating them at the semilocal DFT level, achieving an accuracy comparable with fully self-consistent GW calculations [155]. In the work of Skone et al, [152] a computational protocol was defined to evaluate α and
. Early works evaluated the dielectric constant using the Fermi's golden rule (independent particle approximation) [150] or the random phase approximation [151], or alternatively including the exchange-correlation contribution (local field effects) at GGA level [38]. Model dielectric functions have been used as well [146]. Inclusion of exchange-correlation effects beyond semilocal DFT was pursued in the works of Conesa [152] and Skone et al [153]. The nonlocal contributions to the dielectric response were fully taken into account by explicitly computing perturbed GKS orbitals in a self-consistent way, by means of the coupled-perturbed Kohn–Sham method [154]. The computed dielectric constants turned out to be in much better agreement with experiment compared to the values obtained neglecting local field effects or treating them at the semilocal DFT level, achieving an accuracy comparable with fully self-consistent GW calculations [155]. In the work of Skone et al, [152] a computational protocol was defined to evaluate α and 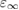 in a self-consistent way, based on the relationship in (4.3), and its performance was assessed with regard to the prediction of band gaps of a set of semiconductors and insulators. The resulting self-consistent hybrid (sc-hybrid) functional has been successfully applied to the study of very diverse condensed systems such as pristine and defective oxides [152, 50], [156], titanates [151], nitrides [157, 158], aqueous solutions [139], and defects in materials for quantum information [159].
in a self-consistent way, based on the relationship in (4.3), and its performance was assessed with regard to the prediction of band gaps of a set of semiconductors and insulators. The resulting self-consistent hybrid (sc-hybrid) functional has been successfully applied to the study of very diverse condensed systems such as pristine and defective oxides [152, 50], [156], titanates [151], nitrides [157, 158], aqueous solutions [139], and defects in materials for quantum information [159].
Along similar lines, the parameters defining range-separated hybrid functionals have been related to the dielectric properties of extended systems. The prototype of these system dependent range-separated hybrids is the screened exchange sX-LDA functional, for which the Thomas-Fermi screened interaction replaces the Coulomb kernel in the EXX energy expression

where the Thomas-Fermi wavevector  , depending on the average valence electron density ρv, is the system-dependent EXX range. Self-consistent screened exchange functionals based on a Penn model for the dielectric constant were developed and used in the works of Shimazaki and Asai [146, 160, 161], In [162] the authors explored the parameter space of short range functionals (defined by the exchange fraction and the screening length), drawing a connection with quasiparticle theory to explain the good performance of HSE functionals in predicting semiconductor band gaps and molecular formation energies. Skone et al [163] devised a range-separated dielectric-dependent hybrid (RS-DDH) in which the long-range exchange fraction was set equal to
, depending on the average valence electron density ρv, is the system-dependent EXX range. Self-consistent screened exchange functionals based on a Penn model for the dielectric constant were developed and used in the works of Shimazaki and Asai [146, 160, 161], In [162] the authors explored the parameter space of short range functionals (defined by the exchange fraction and the screening length), drawing a connection with quasiparticle theory to explain the good performance of HSE functionals in predicting semiconductor band gaps and molecular formation energies. Skone et al [163] devised a range-separated dielectric-dependent hybrid (RS-DDH) in which the long-range exchange fraction was set equal to  as obtained in the sc-hybrid, while the short-range fraction was fixed to 0.25 as in PBE0; the screening length was evaluated using three different nonempirical definitions, showing however that the computed materials properties depend very weakly on the specific choice of this parameter. For a better comparison with sx-LDA, in the following the Thomas-Fermi screening length parameter is considered.
as obtained in the sc-hybrid, while the short-range fraction was fixed to 0.25 as in PBE0; the screening length was evaluated using three different nonempirical definitions, showing however that the computed materials properties depend very weakly on the specific choice of this parameter. For a better comparison with sx-LDA, in the following the Thomas-Fermi screening length parameter is considered.
In table 2 we collect the Kohn–Sham band gaps reported in the recent literature for a set of semiconductors and insulators (excluding transition metal oxides, which are discussed in section 5), ranging from covalent sp semiconductors to strongly ionic compounds. Values computed using system independent (PBE0, B3PW91, HSE06) and system dependent hybrids (sc-hybrid, sx-LDA, RS-DDH) are compared. The mean absolute errors evaluated with respect to experimental values suggest that, for either classes of full-range and range-separated hybrids, system dependent functionals give band gaps in better agreement with experiments. For example, sc-hybrid tends to correct the overestimated (underestimated) values obtained with PBE0 for small (large) gap systems. It is however clear that the sc-hybrid performance is not equally satisfactory for all materials: as shown in [162], it tends to overestimate (underestimate) the gap of materials with dielectric constant smaller (larger) than 4–5, corresponding to large (small) gap materials, at variance with the behavior of PBE0. RS-DDH performs best among all the methods compared. The improvement of RS-DDH over sc-hybrid may be ascribed to a better description of the strongly screened Coulomb exchange interaction in condensed systems. In fact, a similar improvement is observed even for system independent hybrids when screening effects are taken into account (HSE06 versus PBE0).
Table 2. Kohn–Sham band gaps (eV) of selected semiconductors and insulators computed with full-range and range-separated hybrid functionals discussed in the text. Band gaps are evaluated at the experimental geometry. Values obtained from GGA-PBE and one-shot GW calculations using PBE as starting point (G0W0) are reported. The experimental values (exp.) are the those reported in [163]. The mean absolute error (MAE, eV) and mean absolute relative error (MARE, %) with respect to experimental values are reported.
| Full-range hybrids | Range-separated hybrids | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Phase | PBE |
PBE0 |
B3PW91 |
sc-hybrid |
HSE06 |
sx-LDA | RS-DDH |
G0W0 | Exp. | |
| Ge | Diamond | 0.00 | 1.53 | 1.03 | 0.71 | 0.74 | 0.69 |
0.50 |
0.74 | |
| Si | Diamond | 0.62 | 1.75 | 1.62 | 0.99 | 1.21 | 1.07 |
1.02 | 1.17 |
1.17 |
| C | Diamond | 4.15 | 5.95 | 5.80 | 5.42 | 5.43 | 5.38 |
5.45 | 5.59 |
5.48 |
| SiC | Zincblende | 1.37 | 2.91 | 2.71 | 2.29 | 2.32 | 2.52 |
2.32 | 2.25 |
2.39 |
| AlP | Zincblende | 1.64 | 2.98 | 2.85 | 2.37 | 2.42 | 2.21 |
2.42 | 2.49 |
2.51 |
| GaN | Zincblende | 1.88 | 3.68 | 3.39 | 3.26 | 3.08 | 3.27 |
3.30 | 2.80 |
3.29 |
| ZnS | Zincblende | 2.36 | 4.18 | 3.44 | 3.82 | 3.44 | 3.74 |
3.86 | 3.29 |
3.91 |
| BN | Zincblende | 4.49 | 6.51 | 6.29 | 6.33 | 5.91 | 6.12 |
6.34 | 6.19 |
6.40 |
| AlN | Wurtzite | 4.33 | 6.31 | 6.23 | 5.74 | 6.09 |
6.23 | 4.81 |
6.28 | |
| MgO | Rocksalt | 4.80 | 7.25 | 6.93 | 8.33 | 6.59 | 7.72 |
8.22 | 7.08 |
7.83 |
| LiCl | Rocksalt | 6.54 | 8.66 | 8.59 | 9.62 | 8.15 | 9.54 | 9.27 |
9.4 | |
| LiF | Rocksalt | 9.21 | 12.18 | 15.69 | 13.28 | 13.27 |
15.18 | 13.27 |
14.2 | |
| MAE | 1.85 | 0.58 | 0.41 | 0.25 | 0.45 | 0.22 | 0.18 | 0.43 | ||
| MARE | 41.36 | 21.32 | 14.73 | 4.55 | 6.76 | 4.98 | 3.32 | 9.67 | ||
aSkone et al [163, 153]. bSupporting information of [166]. cClark and Robertson [133]. dMoussa et al [162]. eChen and Pasquarello [92]. fShishkin and Kresse [61]. gChen and Pasquarello [79].
4.3. Alternative approaches to system dependent hybrids for semiconductor surfaces and interfaces
The methods reviewed so far propose a definition of a system dependent exchange fraction which is theoretically justified by comparison with approximate forms of the electronic self-energy within the many body GW framework. As far as concerns electronic structure calculations for bulk crystals, the relation  is well justified and gives band gaps and dielectric constants in good agreement with experiment, especially if evaluated self-consistently.
is well justified and gives band gaps and dielectric constants in good agreement with experiment, especially if evaluated self-consistently.
However, the same approach is not applicable when strong spatial variations of the dielectric response are present in the system. This is typically the case for semiconductor surfaces and interfaces, and, to a lesser extent, for defects in bulk crystals. In the latter case, one would not expect the dielectric function to deviate considerably from its value in the pristine (bulk) material, provided that the defect concentration is small enough; dielectric-dependent functionals may thus be safely used to calculate defects properties in the usual supercell approach [155]. However, in the case of surfaces and interfaces, the problem is not easily overcome.
The application of hybrid functionals to surface science problems has increased considerably in the past 10 years. In fact, the issues posed by the self-interaction error crucially affect the description of surface chemical processes of relevance for, e.g. catalysis and photoelectrochemistry [9]. For example, it has been early pointed out that the use of hybrids is essential to correctly describe localized electronic states at prototypical oxide surfaces for photocatalysis such as TiO2 [164]. However, hybrids do not always perform better compared to standard semilocal functionals in surface science studies. For example, for the important problem of the CO adsorption on transition metal surfaces, the performance of different hybrids (HSE and B3LYP) depends more critically on the choice of the semilocal part of the functional (PBE and BLYP), rather than on the inclusion of exact exchange [165]. In general, hybrid functionals should be chosen whenever an accurate description of charge localization and transfer at the surface is pursued. One may think of d electrons at cation sites on transition metal oxide surfaces as a prime example of fundamental importance to understand electrochemical mechanisms at interfaces. More often, in the study of catalytic materials, the less computationally expensive DFT + U approach is adopted to correct self-interaction, often leading to satisfactory results [167].
With regard to the more basic problem of predicting the electronic structure of pristine semiconductor surfaces, the design of hybrid functionals suited for inhomogeneous systems and inspired to many-body self-energy approximations such as GW would be a fundamental step forward, similarly to what self-consistent hybrids represent for electronic structure calculations of bulk crystals. To the best of our knowledge, this question has been mostly unexplored until now. However, the influence of α on the band alignment at semiconductor heterojunctions and on the related issue of defect energy levels positions has been quite extensively investigated. In fact, both the problems can be reduced to the one of computing accurate band edge positions [168]. In one of the earliest investigations concerning this problem, Alkauskas et al [169] studied the band offset at several semiconductor-oxide interfaces by first optimizing the exchange fraction in PBE0 so as to reproduce the experimental bulk band gap for each material separately; an interface calculation with the exchange fraction set to the average between those of the semiconductor and the oxide phases was then performed to obtain a common reference for band edge alignment. Using this approach, remarkable improvement over standard PBE0 (α fixed to 0.25) was achieved in the predicted band edge offsets for the Si/SiO2, 4H–SiC/SiO2, and Si/HfO2 heterojunctions. In a subsequent work, Komsa et al investigated the effect of the exchange fraction and the treatment of the long-range exchange interaction on the bulk band edge shifts for Si, SiC, HfO2 and SiO2 [170]; it was shown that for an optimized α parameter reproducing the experimental band gap, the band edge shifts calculated with the PBE0 and HSE functionals differed by at most 0.2 eV in the case of the large gap insulator SiO2. Very close agreement between the two methods within the mixed scheme proposed in [168] was also obtained for the band offset at the Si/SiO2 interface. However, it was pointed out in a later investigation encompassing a broader set of materials [41] that tuning the exchange fraction to reproduce the bulk band gap obtained in G0W0 does not necessarily imply that the computed band edge positions will be consistent with those calculated at the GW level; in fact, deviations between the two methods were found to be as large as 0.5–1 eV for wide gap insulators such as HfO2, MgO, and SiO2. In a subsequent work, Chen and Pasquarello proposed a nonempirical protocol for fixing a material dependent α, requiring the optimized PBE0-like functional PBE0(α) to give the same band gap obtained in a subsequent G0W0 calculation on top of PBE0(α); [79] this requirement is equivalent to defining an optimal starting point for one-shot G0W0 calculations. The ionization potentials of a set of semiconductor surfaces (Ge, Si, C, GaAs, GaP, ZnSe, ZnO, TiO2) were calculated using this method, which was compared with the results of the empirically tuned functional reproducing the experimental gap. It was found that the empirically tuned PBE0 performs slightly better than PBE0(α), while both methods clearly give better results than PBE. Of course, an empirical tuning may be biased by the lack of clean experimental data, and hence the definition of a theory consistent approach to fix the exchange fraction is certainly preferable.
Recently, Hinuma et al reported the computed band edge positions for several semiconductor surfaces, as well as the natural band offset at a few zincblende semiconductor heterojunctions, comparing different hybrid DFT and GW schemes [171]. They used dielectric-dependent hybrid functionals, where α was set to the inverse dielectric constant computed at the PBE + U and PBE0 level for the bulk material; the exact exchange potential was evaluated non self-consistently, using the PBE wavefunctions and charge densities. The results for band alignment at surfaces were compared to the partially self-consistent GW0 approach and experimental data. Dielectric-dependent hybrids showed good agreement with experimental ionization potential data, improving over HSE and, especially, GW0 for most of the materials (figure 5); the poor performance of the GW0 in predicting band edges may be related to the neglect of vertex corrections, as was pointed out in earlier studies [91, 172].
Figure 5. Ionization potential computed for several semiconductors and insulators at different levels of theory: GW0 on top of PBE (GW0@PBE); non self-consistent (nsc) dielectric-dependent hybrids with exchange fraction fixed at 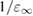 , and the dielectric constant computed using PBE0 (
, and the dielectric constant computed using PBE0 ( ) and PBE + U within the random phase approximation (
) and PBE + U within the random phase approximation (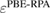 ); non self-consistent HSE06 (nsc-HSE06); semilocal PBE. Original data are reported in [170] (courtesy of F. Oba).
); non self-consistent HSE06 (nsc-HSE06); semilocal PBE. Original data are reported in [170] (courtesy of F. Oba).
Download figure:
Standard image High-resolution imageIn conclusion, for the problem of computing the electronic structure of surfaces and interfaces, material dependent hybrids have been mainly parametrized using bulk properties as a target, and a formulation based on the intrinsic characteristics of these inhomogeneous systems is presently lacking. In this regard, it would be ideal to build position dependence directly into the functional, so as to take into account the spatial variation of the dielectric properties in a natural way; a similar approach have recently been proposed for bulk systems [173], but its generalization to surfaces has not been yet pursued.
4.4. System dependent hybrid functionals for finite systems
It is worth briefly mentioning a few approaches that have been proposed to construct nonempirical system dependent hybrid functionals tailored to finite systems, such as, for example, molecules and nanoparticles. Several different ideas have been developed over the past years. An interesting approach considered a range-separated hybrid in which the range separation parameter was tuned to enforce the validity of the Koopmans' theorem (or equivalently the correspondence with excitation energies computed with the ΔSCF method) [174]; the accuracy of this approach was demonstrated for molecules, nanocrystals [174], and molecular crystals [151]. A similar idea was applied in the context of time-dependent DFT to compute optical spectra of molecules as well as solid state systems, although in the latter case the parameters in the functional were chosen semiempirically [175]. Atalla et al [176] instead proposed to optimize the exchange fraction α so as to minimize the quasiparticle correction, obtained at the G0W0 level, for the highest occupied molecular orbital. This scheme is reminiscent of the nonempirical tuning procedure presented in [60], which was however defined for extended systems. Recently, a generalization of dielectric-dependent hybrid functionals to finite systems was developed [177], in which the exchange fraction was evaluated as the ratio between the matrix elements of the statically screened and the bare exchange self-energies. This scheme, which avoids the difficulties posed by the definition of a dielectric constant for finite systems, can be made self consistent [178] and for condensed systems reduces to the dielectric-dependent hybrid functional described in [152]. It was shown to yield accurate optoelectronic properties of organic and inorganic molecules, as well as nanocrystals.
5. Electronic structure of oxide materials from material-dependent hybrid functionals
5.1. Bulk properties of d0 and correlated transition metal oxides
The electronic structure of oxide materials, and particularly that of correlated transition metal oxides, is notably challenging for density functional methods. This is mainly due to the often mixed itinerant (from oxygen s and p orbitals) and localized (from metal cation d or f orbitals) character of the band edges. Consequently, it is often preferable to treat the localized subset of electronic states separately by using models for correlated electrons, within e.g. DFT + U, or, at a higher level of theory, DMFT.
Alternatively, hybrid functionals treat delocalized and localized states on the same footing, by applying the orbital dependent Hartree–Fock exchange potential to either. Although hybrids are not specifically designed to improve the description of electron correlation over semilocal density functionals, the use of exact exchange leads to a better description of highly localized states important for a qualitatively correct description of the electronic and magnetic structure of correlated oxides.
Hybrid functionals have been used to study transition metal oxides since their first applications to extended systems. Wide gap oxide semiconductors have been extensively investigated using hybrid methods (see [50] and references therein), owing to their broad use in catalysis and optoelectronics and the importance of predicting accurate electronic properties for those applications. The more challenging magnetic rare earth oxides [121] and actinide oxides [179], as well as transition metal monoxides (MnO, FeO, CoO, NiO) [71, 123, 124, 133] have been studied using both full-range and screened exchange hybrids, obtaining qualitatively good results in terms of the predicted magnetic order and the insulating properties of the ground state. Iori et al investigated the electronic structure of binary (VO2, V2O3, Ti2O3) and more complex perovskite oxides (LaTiO3, YTiO3) showing that material independent hybrids such as HSE tend to overestimate the small experimental gap (0.2–0.7 eV) of these magnetic semiconductors, although providing a qualitatively correct description of the correlated electronic states [180]. However, for the description of more complex phenomena such as the metal insulator transition in VO2, even hybrid functionals may not be sufficient [181], and one thus has to resort to explicitly correlated methods like quantum Monte Carlo in order to capture the correct physics [182].
As for sp semiconductors discussed in the previous sections, dielectric-dependent hybrid functionals generally provide a better quantitative description of the band gap and the electronic structure, although with some exceptions. Binary d0 and correlated transition metal oxides have been investigated by Skone et al [152, 162] and Gerosa et al [50] using self-consistent hybrid functionals. In table 3 the computed fundamental gaps for a selection of such oxides is reported. Overall, the sc-hybrid functional gives gaps closer to experiment compared to PBE0, which overestimates them for almost all the considered materials. This improvement is more evident for d0 metal oxides, whereas for correlated oxides the performance is less satisfactory. In fact, while the band gap of CoO is overestimated by more than 1 eV, that of MnO and NiO is smaller than experiment by 0.2–0.3 eV. This behavior does not correlate well with the values of the experimental and theoretical dielectric constants (table 4), based on what one would expect from the relationship 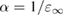 (increasing gap for decreasing dielectric constant). In fact, if one looks at the experimental gap and dielectric constant, this monotonous relationship is not satisfied; even considering the computed values, and assuming that the
(increasing gap for decreasing dielectric constant). In fact, if one looks at the experimental gap and dielectric constant, this monotonous relationship is not satisfied; even considering the computed values, and assuming that the 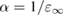 relationship still holds, then the widely verified proportionality between α and the gap would be lost (in fact, CoO and MnO have essentially the same band gap, despite having appreciably different dielectric constants). Thus, dielectric-dependent hybrids seem to perform in an unconventional way for correlated oxides. This behavior may be related to a breakdown of the validity of the arguments for the inverse proportionality of α with the dielectric constant, which are rooted into many-body theory and the quasiparticle description of electronic states.
relationship still holds, then the widely verified proportionality between α and the gap would be lost (in fact, CoO and MnO have essentially the same band gap, despite having appreciably different dielectric constants). Thus, dielectric-dependent hybrids seem to perform in an unconventional way for correlated oxides. This behavior may be related to a breakdown of the validity of the arguments for the inverse proportionality of α with the dielectric constant, which are rooted into many-body theory and the quasiparticle description of electronic states.
Table 3. Fundamental Kohn–Sham band gaps (eV) of selected wide gap oxide semiconductors and transition metal monoxides computed with full-range and range-separated hybrid functionals discussed in the text. Band gaps are evaluated at the experimental geometry, except for values marked with a dagger (†), for which the optimized geometry is considered. Values obtained from GGA-PBE and one-shot GW calculations using PBE as starting point (G0W0) are reported. The experimental values (exp.) are the those reported in [163]. The mean absolute error (MAE, eV) and mean absolute relative error (MARE, %) with respect to experimental values are reported.
| Phase | PBE | PBE0 | B3PW91 |
sc-hybrid | HSE06 | RS-DDH |
G0W0 | Exp. | |
|---|---|---|---|---|---|---|---|---|---|
| TiO2 |
Anatase | 2.18 | 4.23 | 3.66† | 3.59 | 3.73 | 3.42 | ||
| TiO2 | Rutile | 1.81 |
3.92 |
3.05 |
3.39 |
3.17 | 3.27 |
3.3 | |
| ZnO |
Wurtzite | 1.07 | 3.41 | 4.07†, 3.78 |
2.46 |
3.67 | 3.06 |
3.44 | |
| ZrO2 |
Tetragonal | 4.00 | 6.33 | 5.66† | 5.61 | 5.87 | 5.78 | ||
| HfO2 | Monoclinic | 4.32 |
6.65 |
6.68 |
5.83 |
6.67 | 5.67 |
5.84 | |
| WO3 |
Monoclinic | 1.91 | 3.74 | 3.34†, 3.47 |
3.39 |
3.49 | 3.34 |
3.38 | |
| CoO | Rocksalt | 0.00 |
2.82 |
3.06 | 3.62 |
2.82 |
3.98 | 3.4 |
2.5 |
| MnO | Rocksalt | 1.12 |
4.77 |
4.79 | 3.60 |
4.77 |
3.49 | 3.4 |
3.9 |
| NiO | Rocksalt | 0.97 |
4.09 |
3.92 | 4.11 |
4.09 |
4.15 | 4.7 |
4.3 |
| FeO | Rocksalt | 0.00 |
2.63 | 2.41 |
2.2 |
2.4 |
aGerosa et al [51]. bSkone et al [163, 153]. cSupporting Information of [166]. dChen and Pasquarello [41]. eChen and Pasquarello [79]. fRödl et al [70], G0W0@HSE.
Table 4. Electronic dielectric constant 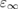 computed with the self-consistent hybrid (sc-hybrid) functional and compared to experiment (exp.). Values are taken from [153].
computed with the self-consistent hybrid (sc-hybrid) functional and compared to experiment (exp.). Values are taken from [153].
| Phase | sc-hybrid | Exp. | |
|---|---|---|---|
| TiO2 | Rutile | 6.56 | 6.34 |
| ZnO | Wurtzite | 3.46 | 3.74 |
| HfO2 | Monoclinic | 3.97 | 4.41 |
| WO3 | Monoclinic | 4.72 | 4.81 |
| CoO | Rocksalt | 4.92 | 5.35 |
| MnO | Rocksalt | 4.45 | 4.95 |
| NiO | Rocksalt | 5.49 | 5.76 |
Recent investigations on non-correlated metal oxides (Cu2O, TiO2, ZrO2, SnO2, ZnO) using dielectric-dependent and self-consistent hybrids are reported in the works of Viñes et al [183] and Fritsch et al [184], confirming the satisfactory performance in predicting band gaps as well as structural properties. In [50], several crystallographic phases of ZnO, TiO2, ZrO2, and WO3 were studied, showing that dielectric-dependent hybrids are able to reproduce well the gap of phases with very different dielectric constants, such as those of cubic and room temperature monoclinic WO3. However, the use of these functionals to predict phase stabilities (in terms of differences in total energies) gave less satisfactory results, particularly when the dielectric constant (and hence α) varies over a wide range of values. Instead, when the difference in α between different phases is not too large, the energetics is reasonably well described, as also observed for the stoichiometry reduction from TiO2 to Ti2O3.
With regard to more complex oxide materials, the screened exchange HSE functional with an optimized α parameter have been systematically applied to the study of the structural, electronic and magnetic properties of 3d perovskites belonging to the LaMO3 (M = Sc–Cu) family, yielding electronic structures in good agreement with experiments and a qualitatively correct description of the character of the electronic ground state [185]. An extensive review of applications of hybrid functionals to perovskites may be found in [186].
5.2. Band alignment at stoichiometric oxide surfaces and interfaces
The study of oxide surfaces and interfaces using dielectric-dependent hybrids has been quite limited, in part due to the conceptual difficulties faced when applying this method to inhomogeneous systems (section 4.3), in part because of the challenges posed by the description of the electronic structure of oxides even in their bulk, pristine phases (section 4.1). Here we give an account of the few studies that have been performed so far in this direction. The effect of the exchange fraction on the band edge shift with respect to PBE results for a few transition metal oxides (ZnO, TiO2, HfO2) and wide gap oxide insulators (SiO2, MgO) was investigated in [40, 60, 169]. As already discussed in section 4.3, tuning α so as to match the computed G0W0 band gap does not always give good results in terms of band edge levels. For HfO2, SiO2 and MgO the discrepancy with GW is particularly large: in fact, an optimally tuned hybrid functional gives a valence band (VB) edge position deeper by 0.4 to 0.7 eV compared to GW band edges [40]. In [60], an optimal hybrid DFT starting point was adopted for G0W0 calculations considering the experimental band gap as the target property to be reproduced. While for ZnO, HfO2, SiO2 and MgO, the VB edge positions computed with the two empirically tuned hybrid DFT and GW methods match almost perfectly (differences < 0.1 eV), for TiO2 the discrepancy turned out to be more than 0.4 eV. Using the nonempirical tuning procedure discussed in section 4.3, this discrepancy was only slightly reduced to 0.3 eV. In the same work, the ionization potentials of the wurtzite ZnO(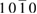 ) and rutile TiO2(1 1 0) surfaces were computed using both empirically and nonempirically tuned hybrids, giving 7.88 eV and 8.12 eV for ZnO (experimental value 7.82 eV), and 8.14 eV and 8.51 eV for TiO2 (experimental values 8.0, 8.2 eV) respectively.
) and rutile TiO2(1 1 0) surfaces were computed using both empirically and nonempirically tuned hybrids, giving 7.88 eV and 8.12 eV for ZnO (experimental value 7.82 eV), and 8.14 eV and 8.51 eV for TiO2 (experimental values 8.0, 8.2 eV) respectively.
Hinuma et al included ZnO and MgO in the set of semiconductor surfaces studied with dielectric-dependent functionals, finding good agreement with the experimental ionization potentials (see figure 5), especially for ZnO; [170] the dielectric-dependent hybrid however was found to give substantial discrepancies with GW0@PBE results, in accord with the general tendency evidenced in the studies of Pasquarello and coworkers. A more systematic study of band edge positions of transition metal oxide surfaces was performed by Toroker et al using standard PBE0 and HSE functionals [187]. For the considered set of oxides (MnO, FeO, Fe2O3, NiO, Cu2O) the position of the VB maximum computed with PBE0 was found to be 0.3–0.5 eV deeper compared to HSE, due to the neglect of the long-range part of the exact exchange interaction in the latter. Even PBE0, however, predicted the VB positions to be too shallow with respect to experiments, although the lack of clean experimental data hindered a careful assessment. Other more system targeted hybrid functional studies of the electronic structure of oxide surfaces have appeared in the recent literature for rocksalt oxides [188], perovskite transition metal oxide surfaces and interfaces [77], and nickel-iron hydroxides [189].
Finally, few studies involving oxide interfaces have been performed using dielectric-dependent or optimally tuned hybrid functionals. Except for the already discussed works of Pasquarello and coworkers, mostly considering wide gap insulators (HfO2, SiO2) and their interfaces with other semiconductors (see section 4.3), empirically tuned functionals have been used to calculate the band offset at the Ge/GeO2 heterojunction [190], and the band alignment at the interface between ZnO and the P3HT polymer, a system of interest for photovoltaic applications [191].
5.3. Hybrid functional calculation of defects in oxides
In the vast majority of technological applications, oxide semiconductors are not used in their pure and fully stoichiometric form but, rather, are functionalized by introduction of specific defects and dopants. The reason is that new electronic, optical, magnetic and chemical properties emerge when impurity atoms or intrinsic defects are incorporated in the lattice. The comprehensive understanding of the physical and chemical properties of defective oxides is a fundamental requirement for a rational and efficient design of new doped semiconducting oxides with tailored properties. This may lead to a more efficient exploitation of these complex systems and to an expansion of the range of their applications.
However, a very high accuracy is required if one is interested in using computational techniques to investigate the electronic structure and properties of defective oxides and to compare the results to experimental measurements. In this respect, the standard approach to simulate point defects in metal oxides has been rooted within DFT and the supercell model. Thermodynamic stability of defects is rather well described by local and semilocal density functional methods [192–194]. On the contrary, similarly to the band gap problem described above, standard DFT methods tend to fail in describing the position of the defect states in the band gap, mostly because they overestimate the degree of defect state delocalization as a consequence of excessive electron self-interaction they provide [195–197].
In this scenario, 'classical' hybrid functionals (B3LYP, PBE0, HSE06, etc), and, more recently, dielectric-dependent hybrid functionals, have been successfully applied to compute impurity and defect states in defective oxide semiconductors.
Although it is a common practice, to estimate the position of the energy levels introduced in the band gap by defects using the one-particle Kohn–Sham eigenvalues is a rather crude approximation. The results are very approximate and, in general, compare poorly with experimental optical absorption or emission spectroscopic data. In principle, an ideally exact exchange-correlation functional could provide exact defect state energies by computation of the defect formation energies for different charge states of the defect, i.e. charge-transition levels or CTLs [198–201]. These quantities can be directly compared to experimentally measured excitation and emission energies for defective oxides. In practice, however, given the limit of current DFT approximations, total energies, and thus also CTLs, are affected by some error. Of course, the more accurate is the exchange-correlation approximation used, the better are the corresponding CTLs. In this respect, the use of exact exchange hybrid DFT methods is a promising approach since they are known to provide band gap values in more quantitative agreement with experiments, as discussed in previous sections. These methods include unscreened, screened, and dielectric-dependent functionals.
The CTLs formalism is based on the calculation of the formation energy of the oxide defect under investigation, e.g. an oxygen vacancy, at fixed conditions of oxygen partial pressure and at T = 0 K. This will only depend on the chemical potential of the electrons (Fermi energy) that can be exchanged between the defect and the host crystal as a consequence of some external perturbation, such as light irradiation. The optical transition level [µopt(q/q')] is defined as the Fermi energy at which the formation energy of the defect ![$\left[ E_{{\rm D}}^{{\rm f}} \right]$](https://content.cld.iop.org/journals/0953-8984/30/4/044003/revision2/cmaa9725ieqn083.gif) in the charge states q and q' become equal. Optical (vertical) excitations obey the Franck–Condon principle, therefore the atomic configuration is kept frozen in the initial conditions. The optical transition level computed with reference to the top of the valence band (εv) is expressed by the following equation:
in the charge states q and q' become equal. Optical (vertical) excitations obey the Franck–Condon principle, therefore the atomic configuration is kept frozen in the initial conditions. The optical transition level computed with reference to the top of the valence band (εv) is expressed by the following equation:
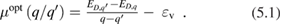
Adiabatic transitions can be described by the thermodynamic transition level [µtherm(q/q')] where ionic relaxations (of energy Erel) are taken into account as follows:
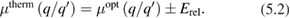
Oxygen vacancy is a common defect in oxides, especially when the sample is prepared in reducing conditions or undergoes high temperature annealing processes. Other typical intrinsic defects are interstitial metal atoms (Mi), interstitial oxygen (Oi), OH groups, peroxo groups, etc. Substitutional impurities, which replace either the lattice metal cations or oxygen anions, may also be present.
In the following we will present an overview on how classical hybrid functionals and dielectric-dependent hybrid functional methods have been exploited to improve the description of defects states in the gap of oxide materials (in terms of CTLs formalism), achieving a substantial agreement with experimental data, when available for comparison.
The situation regarding the understanding of oxygen vacancies in transition metal and rare earth oxides from a theoretical perspective was reviewed in 2007 by Ganduglia-Pirovano et al [202]. In their conclusions, the authors pointed out that: 'Very recent work on the electronic structure of defective TiO2(1 1 0) surfaces [163, 203] using periodic models and hybrid functionals indicates that we can expect an increased interest in this type of calculation in the near future'. With that they foresaw what actually happened in the next ten years. The rather slow diffusion of hybrid functionals for the description of defective materials was related to their high computational cost when a plane wave basis set is used. This is no longer true if one uses a localized basis set (e.g. Gaussian functions as in the CRYSTAL code). With the inclusion of hybrid functionals in popular plane wave based computer codes (e.g. VASP, Quantum ESPRESSO, etc) and the increase in computer power, the use of hybrid functionals has grown regularly and it has become the standard nowadays to treat this kind of problems.
Some works based on hybrid functionals appeared between 2007 and 2009, and the results were compared to GGA and GGA + U methods for the description of intrinsic defects in TiO2 [194, 204–206], and in perovskites, such as PbTiO3, PbZrO3 and SrTiO3 [207]. In these studies, the electronic properties of defects were compared on the basis of the one- particle Kohn–Sham energies.
Starting from 2008 the first works appeared, where the CTLs formalism was applied to defective oxides in the framework of hybrid density functional methods, recognizing their superior capabilities in the description of the defect states position in the band gap. One of the most studied systems in this respect has been the oxygen vacancy (VO) defect in ZnO [208, 209]. This is probably the most controversial native defect in ZnO, since for a long time it has been considered responsible for the unintentional n-type conductivity of ZnO, and classified as a shallow donor species, whereas accurate quantum mechanical calculations indicated it as a deep donor. Since many theoretical studies have been dedicated to this problem, the oxygen vacancy in ZnO can be considered nowadays a prototype system for the investigation of deep and shallow defect states in oxide semiconductors.
The first work by Kresse and coworkers [210] presented defect energetics obtained with the HSE06 hybrid functional which are consistent with the relevant experimental observations, without resorting to any empirical correction for the valence and conduction band positions. Later, Agoston et al [212] applied the unscreened PBE0 and the screened HSE06 hybrid functionals to compute CTLs for VO in In2O3, SnO2 and ZnO and compared the results with LDA and GGA calculations. The main conclusion was that even after a rigid shift correction for the band gap, LDA and GGA methods cannot reproduce the hybrid functional results because they underestimate the relaxation energy at the defect site. One year later, Zunger and coworkers [135] made a similar comparison but considering also a different portion of exact exchange compared to the original one in HSE06. They also studied other intrinsic defects, such as for example the Zn vacancy. In that work they reported that, whereas the various functionals give remarkably uniform results for the formation energies of the charge neutral lattice vacancies of ZnO, significant differences were observed when comparing CTLs. Both these two latter studies were performed using a plane wave basis set and a very limited k-point sampling due to the extremely large cost to compute the nonlocal term for the exact exchange on a large supercell. Just in parallel, another work appeared where some intrinsic and extrinsic defects in ZnO were studied by means of a localized atomic basis set approach [135]. The results are quite in line with plane wave calculations, especially regarding the important role played by the large lattice relaxation, particularly in the case of the doubly charged vacancy, which favors a negative-U character for VO.
Since the default values for the portion of exact exchange (α), e.g. α = 0.20 in B3LYP, and α = 0.25 in PBE0 or HSE06, do not always provide a band gap value in close agreement with experiments, a pragmatic solution has been proposed to vary the value of α so as to fit the experimental band gap. When this is done for the case of ZnO [213] an α = 0.32 is found. However, a parameter value that fits the band gap, not necessarily provides a quantitative description of other properties, such as the energetics of the oxygen vacancy in ZnO. Furthermore, the predictive value of such an approach is very limited since it requires an accurate knowledge of the measured band gap of every material, making studies of unknown materials impossible. The concept of varying the α parameter was further developed by Bruneval and coworkers [214], who studied the dependence of the band edges positions and of the CTLs on the α value in the case of the screened hybrid functional HSE06 for some defects in ZnO and in CdO. The absolute position of the band edges and of the defect states remains a critical issue. In this respect, solutions have been proposed, based also on calculations for defective ZnO. For example, one could resort to a common reference such as the average local electrostatic potential [215]. This approach was found to lead to results which are not sensitive to the particular choice of α.
CTLs for oxygen deficient ZnO, SnO2 and TiO2 by hybrid functional (HSE06) calculations have been compared by Janotti et al to those obtained with the LDA+U approach [216]. The former method was found to be more general and more accurate in the description of both structural and electronic properties and in some cases even essential in order to get a correct picture. Among the hybrid functionals, the screened HSE06 is considered to be the best performing for the study of defect states in oxide semiconductors, especially when shallow states are involved. There is some difficulty by unscreened hybrid functionals to correctly predict and describe this type of states, which was proposed to be related to the long-range exchange interaction [217].
HSE06 thermodynamic transition levels for defective ZnO have been systematically compared [218] to those obtained with the many body ab initio diffusion quantum Monte Carlo (DMC) method. The two DFT approaches yield a correct qualitative description of these materials. For instance, both methods showed similar trends for phase stability and defect energetics under n-type conditions. However, the formation energy of defects in ZnO can differ by over 0.5 eV when evaluated with DMC and the HSE06 functional, whereas the CTLs are in the same range. In any case, the HSE06 hybrid functional was found to outperform all DFT + U approaches considered [217].
Similar studies as those described above for the prototype material, defective ZnO, have been performed for several other defective semiconducting or insulating oxides. Here we provide a list of references, not supposed to be exhaustive, for studies of CTLs from hybrid functional calculations: SiO2, [147, 167, 169] HfO2, [204–206, 219], TiO2 [196, 215, 220, 221] ZrO2, [214, 218, 222], SnO2, [210, 215] Al2O3, [218] LiNbO3 [223], LiMO2 (M = Co, Ni) [224, 225], CdO [213, 226], WO3 [227, 228], β-MnO2 [229], CeO2 [230].
The dependence of the defect states position in the gap on the method used, and in particular on the amount of exact exchange in the exchange-correlation functional (see, e.g., figure 6), is clearly a critical aspect that casts some doubts on the general applicability of these methods. As we discussed before, experience shows that there is no single hybrid functional that is capable to describe at the same level of accuracy, or with the same systematic errors, different kinds of defects in different semiconducting and insulating materials. For this reason, today there is an increasing interest in how self-consistent or dielectric-dependent hybrid functionals perform with respect to the standard hybrid functional, and in particular how these behave when it comes to describe the properties of defective systems. Relatively few studies seem to exist, but the results are quite promising, indicating that such methods can be considered sufficiently robust not only to predict proper band gaps (see section 4.1) but also to describe finer details, such as the defects states position in the band gap. Below we discuss the few examples that have been reported in the literature so far.
Figure 6. Optical charge transition levels for the single ionization of a neutral oxygen vacancy in rutile TiO2, computed with HSE [211], B3LYP [197], and sc-hybrid [156]. The black lines represent the position of the transition level in the gap (blue and red lines represent the valence band maximum and the conduction band minimum, respectively). The energy required to excite one excess electron from the defect state to the conduction band is reported.
Download figure:
Standard image High-resolution imageOxygen vacancies in metal oxides (rutile and anatase TiO2, monoclinic room temperature WO3, and tetragonal ZrO2) have been studied using the self-consistent dielectric-dependent hybrid functional [155], which had previously demonstrated to yield an accurate description of the same pristine oxides [50]. The α value was defined for the bulk pristine crystals and then applied to the corresponding defective system. Two facts justify this procedure: first, this functional properly describes many ground state properties, and the presence of point defects is expected to have a negligible effect on the dielectric properties when their concentration is low. This study showed that this novel approach is capable of reproducing the experimentally observed optical and electrical behavior of sub-stoichiometric defective oxides, through a direct comparison of excitation and emission energies from computed CTLs and experiments. The case of monoclinic WO3 is a bit more complex, being this material highly anisotropic from the structural point of view. For this reason, it has been further investigated in a subsequent work [231], using larger supercells and varying the W–O–W chain orientation for the vacancy site position. A different physical behavior was evidenced in this investigation of the optical and magnetic properties, depending on the orientation considered.
The same methodology was applied [232] to the prototypical problem of the hole localization in Al-doped quartz SiO2. In this system the amount of admixed exact exchange in the hybrid functional was previously shown [233] to be a crucial aspect to properly capture the physical details as known from electron paramagnetic resonance spectroscopy (EPR) [234]. The self-consistently determined α value (for PBE0 calculations) is 46%, which is much higher than the standard values, but can nicely reproduce experimental EPR parameters, although it provides a very poor band structure description. Such result highlights the limits of this methodology when applied to low-dielectric-constant insulator, in contrast to the excellent performances mentioned above for moderate gap metal oxides (dielectric constants ≈4–6).
Similar concerns were discussed by Deak et al [235], concluding that a proper hybrid functional should reproduce not only the band gap, but also satisfy the generalized Koopmans' theorem, i.e. the total energy must be a linear function of the fractional occupation numbers. The authors showed that if this condition is verified, a quantitatively accurate determination of defect level positions in the gap is possible for the case of β-Ga2O3.
Finally, we shall mention that Conesa [151] has applied dielectric-dependent functionals to investigate the effect of N-doping on the electronic structure of various zinc titanates and Galli and coworkers [158] to spin defects in aluminum nitride. These few examples show that there is a potential in the use of dielectric-dependent hybrid functionals for the study of defective oxides and in particular of the CTLs. However, the number of cases discussed in the literature is not yet sufficiently ample to draw very general and universal conclusions. The main advantage of these kind of functionals is that they can be obtained self-consistently, without the need to parametrize the method on more or less accurate experimental values. A limitation is that the portion of exact exchange derived in this way is material dependent, and changes if one moves to a different material but even if one considers another polymorph of the same material. Since the presence of defects, beyond a given concentration, may also result in structural changes and phase transitions, this aspect should be carefully explored in future studies on defective oxides based on dielectric-dependent functionals.
6. Conclusions
In this work, we reviewed recent progress as well as established results in the experimental characterization and the theoretical description of the optoelectronic properties of oxide materials, with particular regard to transition metal oxides. A critical discussion of widely used spectroscopic techniques has been included, emphasizing the sensitivity of the experimentally measured values to the theoretical models used to describe the relevant physical effects; understanding experimental methods is a necessary prerequisite to a sensible benchmarking of theoretical results. On the theoretical side, we discussed the accuracy of state-of-the-art ab initio electronic structure methods in predicting target electronic properties such as the band gap of bulk oxides and the position of band edges at their surfaces, comparing methods rooted in the many-body GW approach and hybrid DFT. Recently proposed dielectric-dependent hybrid functionals have been shown to give a good description of the electronic structure (fundamental band gap) of many oxides, constituting an attractive alternative to more computationally demanding many-body calculations. However, the description of finer details of the electronic structure and optical spectra of these materials often requires adopting a fully many-body approach. This is particularly true for highly correlated oxides, which represent an important challenge for the development of improved many-body approaches as well.
The performance of these methods in describing defects in oxides as well as oxide surfaces has also been discussed. While for defects in the bulk phases dielectric-dependent hybrid functionals provide satisfactory results, both in terms of predicted defect charge stabilities and optical transition energies, the electronic structure of oxide surfaces (e.g. the determination of the ionization potential) poses more challenges, for which the identification of a proper hybrid functional or many-body approach remains an open question.
Acknowledgments
This work was supported by NSF under the NSF center NSF-CHE-1305124 (MG) and the Italian MIUR through the PRIN Project 2015K7FZLH SMARTNESS 'Solar driven chemistry: new materials for photo- and electro-catalysis' (GP). CDV acknowledges funding from the European Research Council (ERC) under the European Union's HORIZON2020 research and innovation programme (ERC Grant Agreement No [647020]). GO acknowledges funding from the EU-H2020 research and innovation programme under grant agreement No 654360 (NFFA-Europe).
MG thanks Giulia Galli, Marco Govoni and Jonathan Skone for stimulating discussions, and Fumiyasu Oba and collaborators for providing data from previous work.