Abstract
Exact analytical results expressed in terms of Bessel functions for the bandgaps, reflectance and transmittance of one-dimensional photonic crystals with a sawtooth refractive index profile on the period are derived, to our knowledge for the first time. This extends the set of exactly solvable models with periodic refractive indices. Asymptotic approximations to the above exact results have been also obtained.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recently there has been a renewal of interest in the properties of one-dimensional (1D) photonic crystals based on graded index slabs. Rauh et al [1] have considered in some detail optical properties of periodic systems consisting of slabs whose permittivities n2(z) increase linearly with depth z. They also considered periodic systems in which alternating layers have quadratically increasing and decreasing permittivities. Their work pointed out the relevance of such 1D photonic crystals for technological applications. They stressed in particular that to a good approximation all the bandgaps have the same width.
Wu et al [2] considered graded crystals with an isosceles triangle profile of the refractive index on the period. They found that the bandgap structure of such crystals is substantially different from the structure of conventional flat-layered crystals: bands can be wider or narrower, depending on the particular form (upward or downward fold) of the triangle. This evidently widens the application areas of 1D photonic crystals in general. However, their results were only obtained numerically. In subsequent publications [3, 4], the same group considered a sawtooth periodic refractive index, and obtained transmissivities greatly exceeding unity, which must raise some doubts about their method.
Very recently, Guasti and Diamant [5] also considered periodic triangular stacks. They found that reflection characteristics are similar to those of a rugate structure if the proper apodization is chosen. The results also illustrate an approximate analytical method for modelling light propagation in inhomogeneous media with discontinuities in the derivatives of the refractive index, developed by the same authors [6].
In this paper we analyse the properties of sawtooth crystals, i.e. 1D photonic crystals constructed of layers with linearly increasing refractive index n(z) in each period, giving a quadratic increase of the permittivity n2(z). Our approach is substantially analytical and, as a result, possible numerical flaws are avoided.
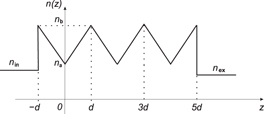
To be precise, for a slab extending from z = 0 to d we take
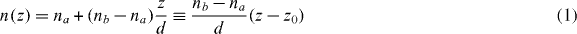
with z0 ≡ − nad/(nb − na). As seen in figure 1 the refractive index is periodic, increasing linearly from na to nb inside each layer, and falls sharply at the cell boundaries. From data in Adachi [7] one finds that the permittivity of the ternary alloy AlxGa1−xAs is approximately linear in the relative content x > 0.4 of Al for wavelengths 10 000 > λ > 6000 Å, so photonic crystals with linearly graded refractive index layers are within present technological possibilities.
Figure 1. 1D photonic crystal with a sawtooth refractive index.
Download figure:
Standard image High-resolution imageWe will express the dispersion equation for the bandgaps of these photonic crystals as well as their reflectance and transmittance in terms of Bessel functions of fractional order. This adds to a group of exactly solvable models of periodic refractive indices which is restricted at the moment to flat-layered periodic structures (binary and ternary photonic crystals) and some specific sinusoidal periodic potentials [8–10]. By means of asymptotic expansions we derive approximate sinusoidal expressions showing that the bandgaps of our sawtooth periodic potential tend to a constant width as the wavelength decreases. For simplicity, as in Rauh's work [1], we restrict our attention to normal propagation.
2. Exact results
Description of optical wave propagation of linearly polarized light of circular frequency ω through a periodic structure, with real refractive index n(z + d) = n(z), in case of normal incidence, reduces from Maxwell's equations to the Helmholtz equation

where the total electric and magnetic fields of propagating light are expressed as

Applying the W transfer matrix method for periodic potentials [11], the field E(z) and its derivative dE(z)/dz ≡ E'(z) at the edge points of the system z = 0 and Nd are related by

where u(z) and v(z) are the so-called normalized solutions, which satisfy the boundary conditions

The Nth power WN of a unimodular W-matrix as occurs in equation (4) can be expressed in terms of W and the unit matrix ![$[\hat {1}]$](https://content.cld.iop.org/journals/1367-2630/15/10/103009/revision1/nj479949ieqn1.gif)
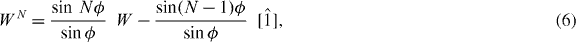
where the dispersion equation for the Bloch phase ϕ takes the form

The advantage of the transfer matrix method is that once we have solved for W of a single layer, the result for N layers is trivial, by use of equation (6).
In dimensionless units, equation (2) with the refractive index defined by equation (1), takes the form

where the dimensionless variable  is
is
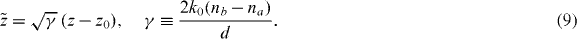
It is straightforward to prove (see appendix A) that the normalized solutions of equation (8) are Bessel functions of order ν = ± 1/4, multiplied by  , i.e.
, i.e.
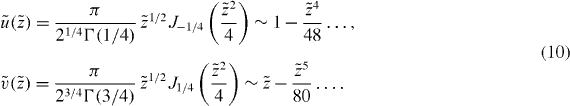
Using standard relations among Bessel functions (see chapter 9 in [12]) one finds

If we now change the variable 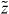 in equation (10) back to the original variable z, we obtain another set of the fundamental solutions,
in equation (10) back to the original variable z, we obtain another set of the fundamental solutions, 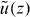 and
and 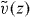 , of equation (2)
, of equation (2)

To construct the matrix W of equation (4), one has to express u(z) and v(z) in terms of 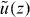 and
and 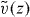 . Taking into account equation (5), one obtains
. Taking into account equation (5), one obtains

where the Wronskian  of the fundamental solutions
of the fundamental solutions  and
and 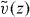 of equation (2) at the point z = 0 is
of equation (2) at the point z = 0 is

With the aid of newly introduced dimensionless parameters,

the values of 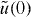 ,
,  ,
, 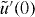 ,
, 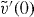 take the form
take the form
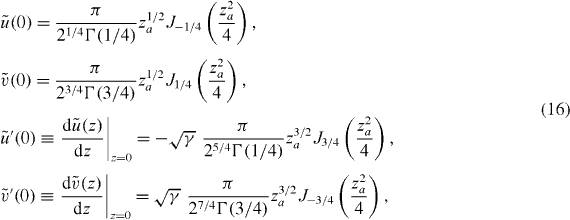
while at z = d, 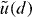 ,
,  ,
, 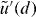 ,
,  are given by
are given by
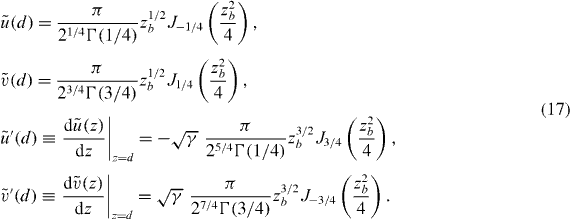
The elements of the W-matrix are then
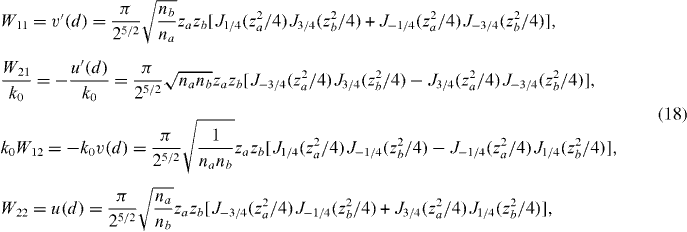
while the dispersion equation (7) takes the form
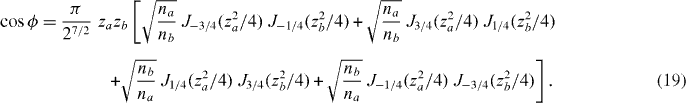
Equation (19) is the exact dispersion relation for our sawtooth 1D photonic crystal. The amplitude reflection r and transmission t coefficients are
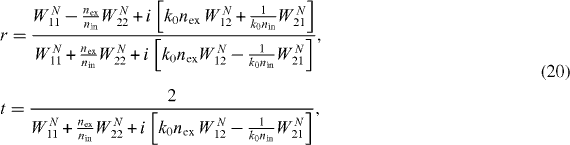
where the elements of the W-matrix are given in exact form by equation (18) and the elements of the WN-matrix are obtained by use of equation (6). The indices of refraction in the incident and exit media are nin and nex as seen in figure 1.
The above results can easily be extended to include an isosceles-triangle refractive index profile, as explained in appendix B.
3. Asymptotic estimates
The motivation for exploring those is to have simple analytic approximations for the Bloch phase cos ϕ, as well as for the reflection and transmission coefficients. Using Hankel's asymptotic formula (section 9.2 of [12]) one obtains the elements of the W-matrix in the form
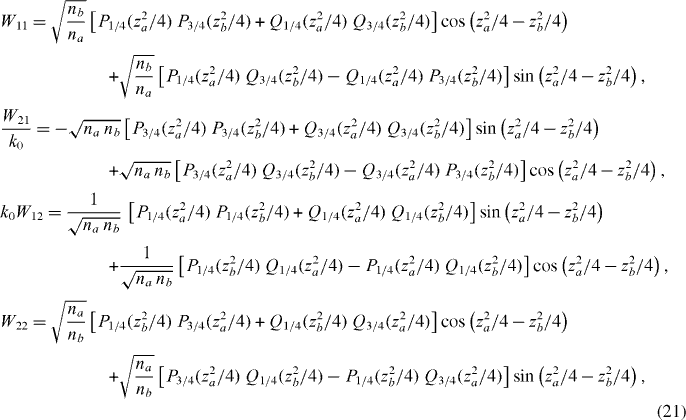
where
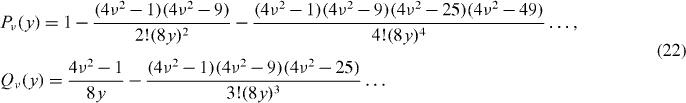
and the dispersion equation in the form
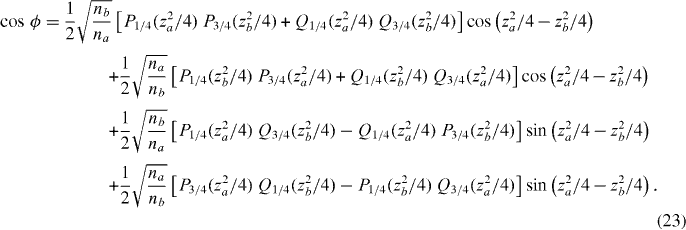
Equations (21)–(23) are the expressions we sought. By truncating the terms Pν and Qν various asymptotic approximations are obtained. In particular, after some trigonometric simplifications, the matrix elements become in the first approximation (P = 1, Q = 0)
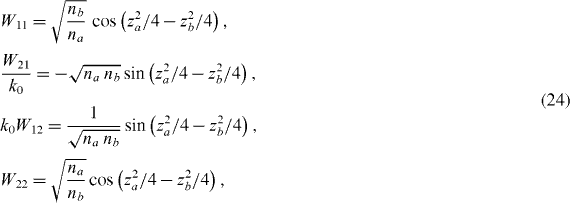
in the second (P = 1, Q = (ν2 − 0.25)/2z)
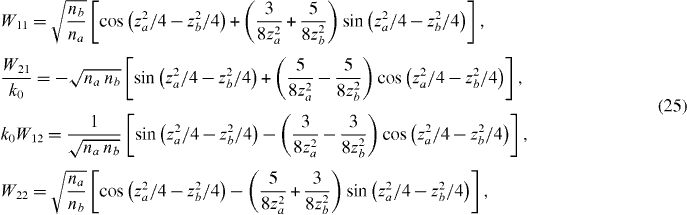
while in the third
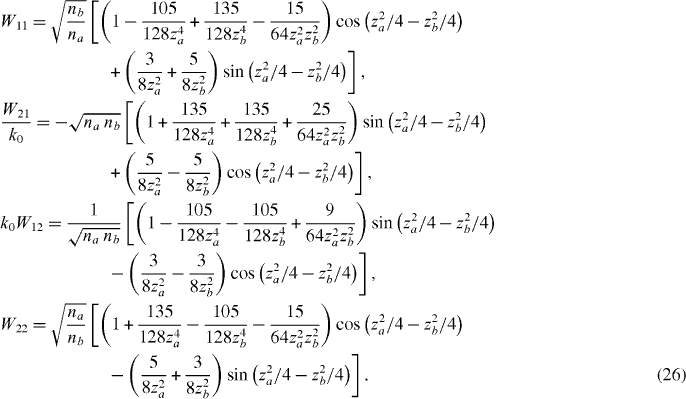
As one can see, the dispersion equation 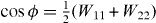 takes a particularly simple form in the first approximation
takes a particularly simple form in the first approximation
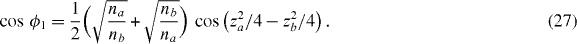
Due to its simplicity equation (27) may be particularly useful in photonic crystal design. Let us estimate its range of validity. Using expressions for W11 and W22 in equations (24) and (25), we find that cos ϕ in the second approximation can be written as
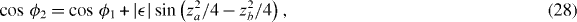
where

At the last line we took into account that for typical dielectrics the refractive indices are in the range na,b = 1...5. As a result, it is safe to use equation (27) for design purposes in the range of wavenumbers k0 such as

Figures 2–4 illustrate all of the above approximations. In the second and third approximations, cos ϕ can also be written as
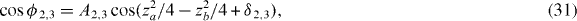
which allows for a shift of both the band centres and their widths. For our choice of nb/na = 2, the amplitude in the first approximation A1 = 1.06 accounts for the narrow bandgaps observed in the drawings.
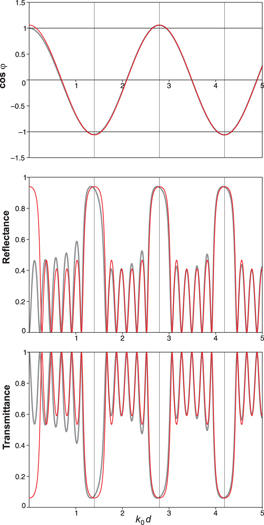
Figure 2. Exact results (thicker grey lines) (see equations (18)–(20)) versus the first asymptotic approximation (thinner red lines) (see equation (24)) for the Bloch phase, reflectance and transmittance, for a sawtooth periodic structure with na = 1.5, nb = 3 and the number of periods N = 6, in the case of normal incidence. The refractive indices outside the structure are nin = 1.0 for z < 0 and nex = 1.0 for z > Nd.
Download figure:
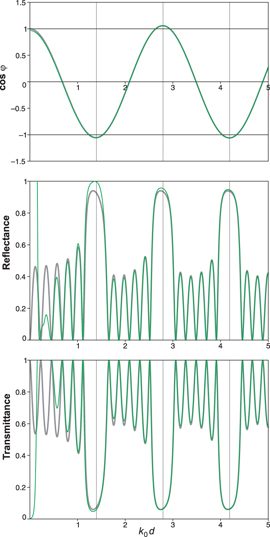
Standard image High-resolution imageFigure 3. Exact results (thicker grey lines) (see equations (18)–(20)) versus the second asymptotic approximation (thinner green lines) (see equation (25)) for the Bloch phase, reflectance and transmittance, for a sawtooth periodic structure with parameters as in figure 2.
Download figure:
Standard image High-resolution imageFigure 4. Exact results (thicker grey lines) (see equations (18)–(20)) versus the third asymptotic approximation (thinner blue lines) (see equation (26)) for the Bloch phase, reflectance and transmittance, for a sawtooth periodic structure with parameters as in figure 2.
Download figure:
Standard image High-resolution imageIn appendix C we also compare the exact results to approximations provided by binary photonic crystals (replacing the ramp by discrete steps).
4. Bandgap analysis
Figure 2 shows that the dispersion equation for cos ϕ in the first approximation is already in quite good agreement with the exact results. We now discuss some of the predictions for the bandgaps that follow from it. The bandgap edges are defined by the condition cos ϕ = (− 1)q, where the index q = 1,2,... numbers the bandgaps. This condition applied to equation (27) leads to expressions for the right kr0 and left kl0 bandedges in the first approximation:

where
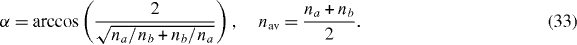
Therefore, the centres of the bandgaps kc0 and their widths w are given in the first approximation by

This is qualitatively similar to the asymptotic results obtained by Rauh et al [1]. In figure 5 we compare the accuracy of the three approximations for the bandgap centres, and in figure 6 for their widths. As one can see from equations (24)–(26), each approximation incorporates new corrections of orders 1/z 2a,b and their squares, respectively. With the exception of the first bandgap (but that is inherent in use of an asymptotic series), all three approximations provide one with quite accurate estimates and the second one balances accuracy and simplicity.
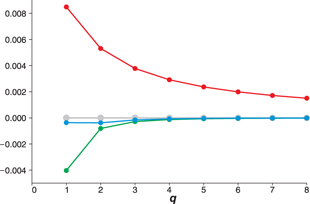
Figure 5. Dimensionless difference, (kc0,a − kc0) d, a = 1,2,3, between exact results, kc0 d, and a given asymptotic approximation, kc0,a d, for bandgap centres of a sawtooth periodic array with refractive index parameters na = 1.5, nb = 3.0 versus the bandgap index q for the first eight bandgaps. From top to bottom the lines are (kc0,1 − kc0) d (red), (kc0 − kc0) d (grey), (kc0,3 − kc0) d (blue), (kc0,2 − kc0) d (green).
Download figure:
Standard image High-resolution imageFigure 6. Dimensionless bandgap widths, w d, for a sawtooth periodic array with refractive index parameters na = 1.5, nb = 3.0 versus the bandgap index q for the first eight bandgaps. From top to bottom the lines are the second asymptotic approximation (green), the first asymptotic approximation (red), exact result (grey) and the third asymptotic approximation (blue).
Download figure:
Standard image High-resolution image5. Conclusion
We have derived the exact dispersion equation, reflection and transmission coefficients, in terms of Bessel functions, for our one-dimensional photonic crystal with a sawtooth refractive index profile. Using the Hankel expansion, we worked out the first three asymptotic approximations to those coefficients. Even the first approximation, which has a particularly simple analytic form, provides one with very reasonable estimates. Using the results of appendix A, one can easily work out solutions for any monomial behaviour (k0n(z))2 ∼ (z/L)n of the permittitivity within a single cell of the periodic system. They always involve Bessel functions J±m(z) of order m = 1/(n + 2).
Acknowledgments
We acknowledge support by FIS2011-24154 and FIS2009-SGR1289 (JM), and by NSERC discovery grant no. RGPIN-3198 (DWLS). We thank one of the referees for suggesting the addition of appendix B.
Appendix A.: Solutions of the wave equation for power law potentials
While discussing the Wentzel–Kramers–Brillouin approximation, Schiff [13, p 272] points out that when k2(z) = (z/L)n, an exact solution of the stationary state wave equation

is given by
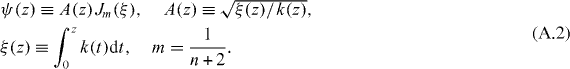
The task is to show that Jm(ξ) is a generic Bessel function of order m, a result given originally by Langer [14]. The most used case is a linear turning point with n = 1⇒m = 1/3, where the solution coincides with the Airy function. The general result makes it easy to work out the transfer matrix for a 1D photonic crystal whose refractive index profile has any monomial 'sawtooth shape' in each layer. To begin, we note that for our assumed k2(z)
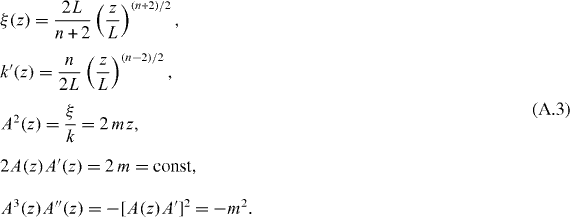
From here we work out ψ' and ψ'', and substitute into the wave equation. On functions of z, the prime means d/dz, but on the Bessel function it means d/dξ. We have
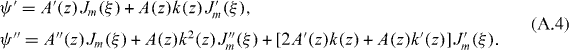
Substituting into the wave equation and removing the factor Ak2, we find that the coefficient of J'm(ξ) is

see equation (A.8) for details, while the coefficient of Jm(ξ) is 1 + [A''/Ak2], where the variable portion is
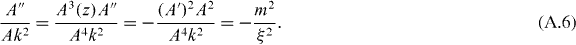
This verifies that the wave equation has been reduced to Bessel's equation for the fractional order m,
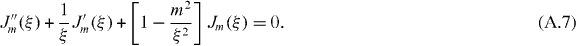
The regular solution Jm(ξ) will vanish at the origin when m > 0, so the irregular solution J−m(ξ) is also required if a non-zero initial value is in order. In equation (A.5) we used the following relations:
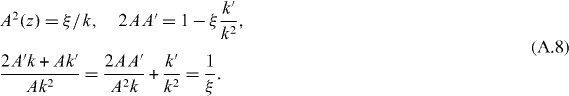
Appendix B.: Triangular profile
Our purpose here is to show how the results of the section 2 can be used to describe wave propagation through a periodic structure with a triangular refractive index profile, see figure B.1. Since the refractive index of the period with −d ⩽ z ⩽ d is an even function, the normalized solutions u and v, relating the field E(z) and its derivative dE(z)/dz at the edge points z = ± d, can be taken to be the even and odd functions, respectively. As a result, we have

where

The dispersion equation takes the form

Expressions for the elements u(d), u'(d), v(d) and v'(d) are given by equation (18).
Figure B.1. 1D photonic crystal with a triangular refractive index.
Download figure:
Standard image High-resolution imageReversing the order of the two matrices whose product gives Wt in equation (B.2) would give the transfer matrix for the inverted V triangle pattern. That is to say, if figure B.1 is a pattern DUDUDU, the new pattern would be UD UD UD. These are examples of biperiodic superlattices [16], and some interesting physics arises if one of the two components U or D is given a slightly different width dU ≠ dD.
Appendix C.: Binary approximations
We consider a binary photonic crystal composed of layers of constant refractive indices n1, n2, with corresponding thicknesses d1, d2. The elements of a binary W-matrix are well-known [11] and given by
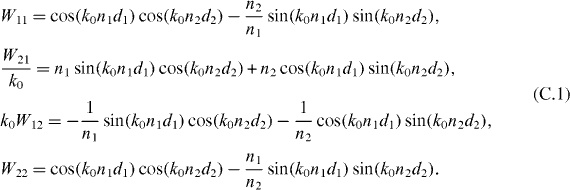
The simplest binary approximation to the sawtooth profile discussed above is given by n1 = na, n2 = nb and d1 = d2 = d/2. Figure C.1 compares the exact results for the sawtooth potential with parameters as in figure 2 to that of the simplest binary approximation. As one can see there are some similarities, but the bandgap widths differ strongly; for example, the third bandgap of the sawtooth potential disappears entirely. A better binary approximation, see figure C.2, is obtained if one follows the recipe of Kalotas and Lee [15], taking the layer indices to be n1 = (na + 3nb)/4, n2 = (3na + nb)/4 and widths d1 = d2 = d/2. (These values give the correct average wave number in each layer.)
Figure C.1. Exact results (thicker grey lines) for a sawtooth periodic potential with parameters as in figure 2 versus binary approximation (thinner black lines) with n1 = na, n2 = nb.
Download figure:
Standard image High-resolution imageFigure C.2. Like figure C.1 but with n1 = (na + 3nb)/4, n2 = (3na + nb)/4.
Download figure:
Standard image High-resolution image