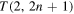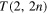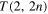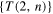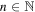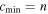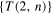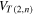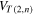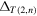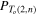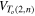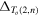Abstract
In this paper we derive and compare numerical sequences obtained by adapted polynomials such as HOMFLYPT, Jones and Alexander-Conway for the topological cascade of vortex torus knots and links that progressively untie by a single reconnection event at a time. Two cases are considered: the alternate sequence of knots and co-oriented links (with positive crossings) and the sequence of two-component links with oppositely oriented components (negative crossings). New recurrence equations are derived and sequences of numerical values are computed. In all cases the adapted HOMFLYPT polynomial proves to be the best quantifier for the topological cascade of torus knots and links.
Export citation and abstract BibTeX RIS
Communicated by Philip Boyland
1. Adapted knot polynomials for vortex knots
In recent years the present authors have shown that adapted knot polynomials can be usefully employed to study and quantify topological complexity of fluid knots (vortex or magnetic)(Liu and Ricca 2012, 2015). These adapted polynomials are function of knot type and fluid conserved quantities (such as vortex strength), and represent new powerful invariants of ideal fluid mechanics (Ricca and Liu 2014). In 2016, stimulated by the laboratory experiments of Kleckner and Irvine (2013) on the production and decay of vortex knots in water, and by the work of Shimokawa et al (2013) on recombinant DNA plasmid reactions, we have applied the adapted the HOMFLYPT polynomial to study the alternate sequence of torus knots 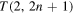 and torus links
and torus links 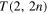 (n positive integer) of co-oriented components, when they progressively untie under the assumption of decreasing topological complexity, due to a single reconnection event at a time (see figure 1). We found that under certain simplifying assumptions the alternate cascade from
(n positive integer) of co-oriented components, when they progressively untie under the assumption of decreasing topological complexity, due to a single reconnection event at a time (see figure 1). We found that under certain simplifying assumptions the alternate cascade from 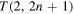 to
to 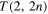 (as
(as 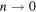 ) can be detected by a unique, monotonically decreasing sequence of HOMFLYPT numerical values (Liu and Ricca 2016).
) can be detected by a unique, monotonically decreasing sequence of HOMFLYPT numerical values (Liu and Ricca 2016).
Figure 1. Top: topological cascade of torus knots and co-oriented links by single reconnection events. Bottom: monotonically decreasing sequence of corresponding HOMFLYPT numerical values.
Download figure:
Standard image High-resolution imageThe derivation of the HOMFLYPT polynomial for fluid knots has allowed the interpretation of the two standard variables of this polynomial in terms of the average values of writhe and twist, and it has also helped to understand the physical implications of the analytical constraints that reduce the two HOMFLYPT variables to a single variable of other knot polynomials, such as Jones and Alexander-Conway. The scope of this paper is to re-examine the numerical sequence obtained by HOMFLYPT and compare it with the numerical sequences obtained by Jones and Alexander-Conway polynomials. In doing so we shall also consider the case of a cascade of torus links 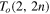 , whose components are oppositely oriented and compare the results. This will give us useful indications as to which polynomial is best suited to detect and quantify topological cascade processes. The material is arranged as follows. In section 2 we briefly recall the results obtained by HOMFLYPT for the sequence of figure 1. In section 3 we derive the expressions of Jones and Alexander-Conway polynomial for the sequence above and compute the numerical values. We then apply HOMFLYPT to the case of links with oppositely-oriented components (section 4), compute the results and compare these to the results obtained by deriving Jones and Alexander-Conway polynomials from HOMFLYPT (section 5). Conclusions are drawn in the final section.
, whose components are oppositely oriented and compare the results. This will give us useful indications as to which polynomial is best suited to detect and quantify topological cascade processes. The material is arranged as follows. In section 2 we briefly recall the results obtained by HOMFLYPT for the sequence of figure 1. In section 3 we derive the expressions of Jones and Alexander-Conway polynomial for the sequence above and compute the numerical values. We then apply HOMFLYPT to the case of links with oppositely-oriented components (section 4), compute the results and compare these to the results obtained by deriving Jones and Alexander-Conway polynomials from HOMFLYPT (section 5). Conclusions are drawn in the final section.
2. HOMFLYPT polynomial for the alternate sequence of knots and co-oriented links
In (Liu and Ricca 2016) we considered the topological cascade sequence of torus knots and links shown in figure 1 under the following assumptions:
- A1. All torus knots
 and links
and links  (with
(with  ) are standardly embedded on a mathematical torus in closed braid form.
) are standardly embedded on a mathematical torus in closed braid form. - A2. All torus knots
 and links
and links  form an ordered set
form an ordered set  (
( ) of elements listed according to their decreasing value of topological complexity given by their minimum number of crossings
) of elements listed according to their decreasing value of topological complexity given by their minimum number of crossings  .
. - A3. Any topological transition between two contiguous elements of
 is determined by a single, anti-parallel reconnection event (Laing et al 2015).
is determined by a single, anti-parallel reconnection event (Laing et al 2015).
By applying the standard HOMFLYPT skein relations, given by
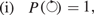

in the independent variables a and z, we can compute the polynomial PK for any given knot K. Explicit computations of some basic examples are given in (Liu and Ricca 2015). By applying equations (1)–(2) to the ordered set 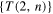 one can prove the following general result (Liu and Ricca 2016).
one can prove the following general result (Liu and Ricca 2016).
Theorem (Liu and Ricca 2016). Let us consider the ordered set 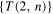
 integer,
integer,  of torus knots and links. The HOMFLYPT polynomial
of torus knots and links. The HOMFLYPT polynomial 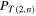 of
of 
 is given by
is given by
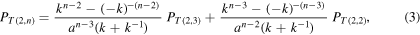
where 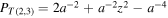 and
and 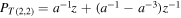 .
.
Initial values are given by the HOMFLYPT computation of the 2-component unlink unknot 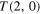 , unknot
, unknot 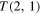 , Hopf link
, Hopf link 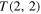 and trefoil knot
and trefoil knot 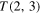 . In general, for any physical knot/link K of writhe Wr, twist Tw and unit strength (flux of vorticity), we have (Liu and Ricca 2015)
. In general, for any physical knot/link K of writhe Wr, twist Tw and unit strength (flux of vorticity), we have (Liu and Ricca 2015)

with 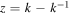 and uncertainty (probability) factors
and uncertainty (probability) factors 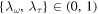 . Consistently with the above assumptions, let
. Consistently with the above assumptions, let 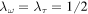 (equivalent to an equi-distribution of uncertainty of writhe and twist values) and
(equivalent to an equi-distribution of uncertainty of writhe and twist values) and 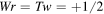 (admissible values of writhe and twist of standardly embedded positive torus knots (Oberti and Ricca 2016). Hence, the sequence of numerical values shown in figure 1 and reproduced in the table of figure 3 is obtained by taking
(admissible values of writhe and twist of standardly embedded positive torus knots (Oberti and Ricca 2016). Hence, the sequence of numerical values shown in figure 1 and reproduced in the table of figure 3 is obtained by taking

Note that a different choice of 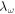 and
and  values would simply produce a vertical shift of the numerical sequence in the plot.
values would simply produce a vertical shift of the numerical sequence in the plot.
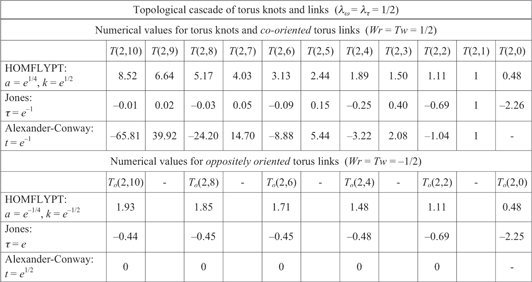
Figure 3. Numerical values of HOMFLYPT, Jones and Alexander-Conway adapted polynomials for the sequence  and
and 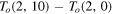 . Note that
. Note that 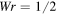 for co-oriented link components (with positive crossings) and
for co-oriented link components (with positive crossings) and 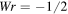 for oppositely oriented link components (with negative crossings).
for oppositely oriented link components (with negative crossings).
Download figure:
Standard image High-resolution image3. Jones and Alexander-Conway polynomials for the alternate sequence of knots and co-oriented links
3.1. Jones polynomial 
The HOMFLYPT polynomial PK degenerates to the Jones polynomial VK when we take
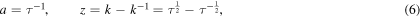
where τ is the new polynomial variable. The standard Jones polynomial is indeed a single-variable polynomial obtained by combining the two HOMFLYPT variables according to 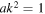 , i.e.
, i.e. 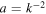 . For physical knots this amounts to a framing prescription on the admissible values of writhe (through z) and twist (through a), given by
. For physical knots this amounts to a framing prescription on the admissible values of writhe (through z) and twist (through a), given by
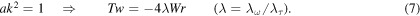
If we take  , then
, then 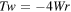 , that for
, that for 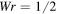 we have
we have 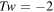 , that represents a rather peculiar constraint for fluid systems. In any case, by taking (6) the skein relations of the Jones polynomial reduce to
, that represents a rather peculiar constraint for fluid systems. In any case, by taking (6) the skein relations of the Jones polynomial reduce to
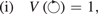
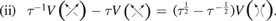
Explicit computations of some basic examples are given in (Liu and Ricca 2012). By substituting the positions (6) into (3), and after some straightforward algebra, we obtain the Jones polynomial 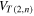 for the ordered set
for the ordered set 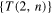
 :
:
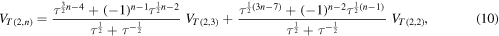
with 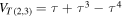 and
and 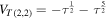 .
.
3.2. Numerical values for the sequence of 
According to Ricca and Liu (2014) (section 6, equation (16)) it is reasonable to take

Hence, by (10) and the position above we have
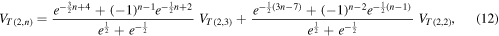
with
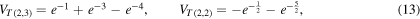
and (Ricca and Liu (2014), section 6, equation (17))

The numerical values of 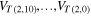 are shown in the table of figure 3. As we see, the Jones sequence is, in absolute values, a monotonically growing sequence as
are shown in the table of figure 3. As we see, the Jones sequence is, in absolute values, a monotonically growing sequence as 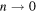 . In terms of signed numbers we actually have two distinct sequences, one of positive values for knots and one of negative values for two-component links, both growing with decreasing values of n.
. In terms of signed numbers we actually have two distinct sequences, one of positive values for knots and one of negative values for two-component links, both growing with decreasing values of n.
3.3. Alexander-Conway polynomial 
The HOMFLYPT polynomial PK degenerates to the Alexander-Conway polynomial 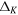 when we set
when we set

where t is the new polynomial variable. The skein relations of the Alexander-Conway polynomial reduce to

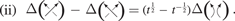
As above, by substituting the positions (15) into (3), and after some straightforward algebra, we obtain the Alexander-Conway polynomial 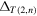 for the ordered set
for the ordered set 
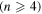 :
:
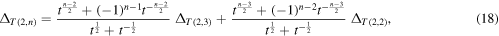
where 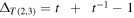 and
and 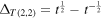 .
.
3.4. Numerical values for the sequence of 
We take

Hence, by (18) and the position above, we have
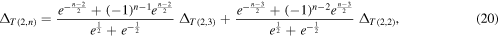
with
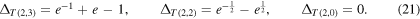
The numerical values of 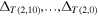 are shown in the table of figure 3. As we see the Alexander-Conway sequence is, in absolute values, a monotonically decreasing sequence as
are shown in the table of figure 3. As we see the Alexander-Conway sequence is, in absolute values, a monotonically decreasing sequence as 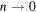 . Similarly to Jones, in terms of signed numbers we actually have two distinct sequences, one of positive values for knots and one of negative values for two-component links, both decreasing with decreasing values of n.
. Similarly to Jones, in terms of signed numbers we actually have two distinct sequences, one of positive values for knots and one of negative values for two-component links, both decreasing with decreasing values of n.
4. HOMFLYPT polynomial for the sequence of links with oppositely oriented components
In the case of torus links with oppositely oriented components the family 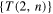 reduces to the ordered set
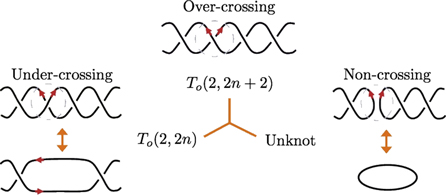
reduces to the ordered set 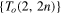 . By direct application of the HOMFLYPT skein relations (1)–(2) we can see (figure 2) that at every reduction step we have the production of a torus link of lower topological complexity, and of an unknot. Hence, we can prove the following result in full generality.
. By direct application of the HOMFLYPT skein relations (1)–(2) we can see (figure 2) that at every reduction step we have the production of a torus link of lower topological complexity, and of an unknot. Hence, we can prove the following result in full generality.
Figure 2. Application of the skein relation (2) to a portion of torus knot/link diagram. The over-crossing (top diagram, encircled region) is converted to the under-crossing (left diagrams) and the non-crossing (right diagrams). Double arrows denote topological equivalence.
Download figure:
Standard image High-resolution imageLemma. Let us consider the ordered set of oppositely oriented torus links 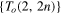
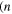 integer,
integer,  . The HOMFLYPT polynomial
. The HOMFLYPT polynomial 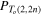 is given by
is given by
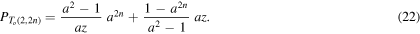
Proof. Let us apply the skein relations (1)–(2) to the top diagram of figure 2. We have

that is

By applying the same relation recursively, we have

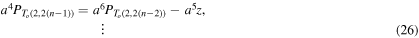
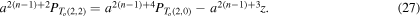
By substituting the l.h.s. term of equation (25) into the r.h.s. of (24) and by doing the same for the subsequent terms in the equations above, we obtain
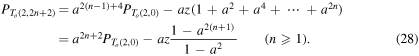
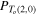 denotes the polynomial of a disjoint union of two unknots given by Liu and Ricca (2015) section 4.1, equation (4.2):
denotes the polynomial of a disjoint union of two unknots given by Liu and Ricca (2015) section 4.1, equation (4.2):

Thus, we have

or, equivalently
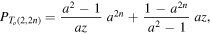
that proves the Lemma. ■
4.1. Numerical values for the sequence of 
Without loss of generality we can take  and
and 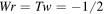 (admissible values of writhe and twist of standardly embedded negative torus links (Oberti and Ricca 2016). Hence, we have
(admissible values of writhe and twist of standardly embedded negative torus links (Oberti and Ricca 2016). Hence, we have

and according to (28), we have numerically:
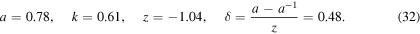
Hence, for HOMFLYPT we have
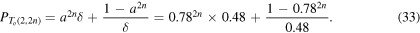
The numerical values of 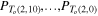 are shown in the table of figure 3. For oppositely oriented components (negative crossings) the sequence decreases with decreasing values of n. This behavior is consistent with that obtained for the alternate sequence of torus knots and co-oriented links.
are shown in the table of figure 3. For oppositely oriented components (negative crossings) the sequence decreases with decreasing values of n. This behavior is consistent with that obtained for the alternate sequence of torus knots and co-oriented links.
5. Jones and Alexander-Conway polynomials for the sequence of links with oppositely-oriented components
5.1. Jones polynomial 
As mentioned in section 3.1 HOMFLYPT degenerates to Jones by taking equations (6). Thus, equation (22) reduces to
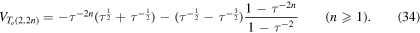
5.2. Numerical values for the sequence of 
As above, we can take the same uncertainty value for Jones and the average writhe  for standardly embedded negative torus links; then, we have
for standardly embedded negative torus links; then, we have 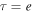 . By substituting this value into (34), we have
. By substituting this value into (34), we have
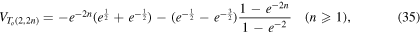
with (Ricca and Liu (2014), equation (6))

The numerical values of  are shown in the table of figure 3. The Jones sequence is given by negative numbers that decrease with decreasing values of n.
are shown in the table of figure 3. The Jones sequence is given by negative numbers that decrease with decreasing values of n.
5.3. Alexander-Conway polynomial 
6. Concluding remarks
In this paper we have derived and compared the numerical sequences obtained by HOMFLYPT, Jones and Alexander-Conway adapted polynomials for the topological cascade of torus knots and links that progressively untie by a single reconnection event at a time. For this we considered two cases: the first case is given by the alternate sequence of knots and co-oriented links (with positive crossings) considered in (Liu and Ricca 2016), the second case is given by the sequence of two-component links with oppositely oriented components (negative crossings). In the first case contrary to HOMFLYPT, that provides a monotonically decreasing sequence of numerical values for decreasing complexity, both Jones and Alexander-Conway give distinct sequences of positive and negative numbers—respectively for knots and links. In absolute values both sequences show uniform, monotonic behavior, that is increasing for Jones and decreasing for Alexander-Conway. It is also interesting to compare the relative jumps in numerical values within each sequence: we notice that these are more marked for HOMFLYPT and Alexander-Conway than Jones, so that for numerical implementation the former probably represents more robust and reliable information. Moreover, if we consider the topological complexity rate given by the ratio between the polynomial value and the topological number of crossings we find that with the exception of the unknot we have 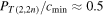 for the first knot/link types (
for the first knot/link types ( ), with this value slightly increasing as n increases (for
), with this value slightly increasing as n increases (for 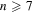 ).
).
In the case of the sequence of torus links with oppositely oriented components we derived a new, general recurrence equation for HOMFLYPT and examined the numerical sequences of all polynomials. In this case too the HOMFLYPT sequence has been found to be uniformly monotonically decreasing with decreasing complexity over the whole cascade. Jones gives a decreasing sequence, whereas Alexander-Conway does not provide any useful information. In summary, HOMFLYPT provides a consistent, reliable and robust numerical information, proving to be the best quantifier to detect and quantify topological complexity for cascades of vortex torus knots and links. We hope to be able to extend this approach to more complex families of knots and links relevant to physical processes characterized by topological transitions. Work is in progress to apply this approach to analyze data from numerical simulations of superfluid vortex tangles.
Acknowledgments
Financial support from the Natural Science Foundation of China (NSFC), Grant No. 11572005, is kindly acknowledged. XL wishes to express his gratitude to the Haiju Project Fellowship (Beijing).