-
PDF
- Split View
-
Views
-
Cite
Cite
Miccal T. Matthews, James M. Hill, Flow around nanospheres and nanocylinders, The Quarterly Journal of Mechanics and Applied Mathematics, Volume 59, Issue 2, May 2006, Pages 191–210, https://doi.org/10.1093/qjmam/hbj003
Close - Share Icon Share
Abstract
For micro- and nanoscale problems, boundary surface roughness often means that the usual no-slip boundary condition of fluid mechanics does not apply. Here we examine the steady low-Reynolds-number flow past a nanosphere and a circular nanocylinder in a Newtonian fluid, with the no-slip boundary condition replaced by a boundary condition which attempts to account for boundary slip due to the tangential shear at the boundary. We apply the so-called Navier boundary condition and use the method of matched asymptotic expansions. This model possesses a single parameter to account for the slip, the slip length  , which is made dimensionless with respect to the corresponding radius, which is assumed to be of the same order of magnitude as the slip length. Numerical results are presented for the two extreme cases,
, which is made dimensionless with respect to the corresponding radius, which is assumed to be of the same order of magnitude as the slip length. Numerical results are presented for the two extreme cases,  = 0 corresponding to classical theory, and
= 0 corresponding to classical theory, and  → ∞ corresponding to complete slip. The streamlines for
→ ∞ corresponding to complete slip. The streamlines for  > 0 are closer to the body than for
> 0 are closer to the body than for  = 0, while the frictional drag for
= 0, while the frictional drag for  > 0 is reduced below the values for
> 0 is reduced below the values for  = 0, as might be expected. For the circular cylinder, results corresponding to
= 0, as might be expected. For the circular cylinder, results corresponding to  → ∞ are in complete accord with certain low-Reynolds-number experimental results, and this excellent agreement is much better than that predicted by the no-slip boundary condition.
→ ∞ are in complete accord with certain low-Reynolds-number experimental results, and this excellent agreement is much better than that predicted by the no-slip boundary condition.
1 Introduction
For many micro or nano flow problems, the boundary surface roughness may well be significant in comparison to the dimensions of the molecules or nanoparticles involved in the flow. In this event the usual no-slip boundary condition of fluid mechanics clearly does not apply, and must be replaced by a condition which reflects boundary slip as a consequence of the tangential shear at the boundary. The simplest linear boundary condition to accommodate this is the so-called Navier boundary condition, which has been in the literature for many years, and postulates that the boundary slip is directly proportional to the tangential shear at the boundary, and the constant of proportionality is referred to as the slip length. In this paper we consider the two model problems of low-Reynolds-number flow around nanospheres and nanocylinders, assuming the Navier boundary condition with a constant slip length. For the sphere a corresponding macroscopic problem might be the flow around a dimpled golf ball, for which it is well known that the surface indentations generate reduced drag, which not only makes the ball go further but its flight is more predictable than that of an equivalent ball with a smooth surface. Indeed the reduced drag is one consequence predicted from the analysis presented here.
The steady flow of a Newtonian fluid past a sphere and a circular cylinder is a fundamental problem, first considered by Stokes (1) in the limit of zero Reynolds number R, that is, the inertial forces are neglected with respect to viscous forces in the Navier–Stokes equations. Solutions were obtained by Stokes for the sphere, but for the circular cylinder no solution was possible, leading to the well-known Stokes' paradox. Later, Whitehead (2) attempted to improve on Stokes' original solution for the sphere by obtaining higher approximations for the flow when the Reynolds number is not negligibly small, by using an iterative procedure on the full Navier–Stokes equations, beginning the process with the solution of Stokes. Whitehead found that no second approximation could be found, leading to Whitehead's paradox.
Both paradoxes were eventually overcome by Oseen, who took the inertial terms of the Navier–Stokes equation partially into account by assuming that the components of velocity could be represented as the sum of a constant (the far-field velocity) and a perturbation term (see Schlichting (3)). Higher-order terms of the Oseen solution may be found, but their value is minimal due to the underlying assumptions required to transform the Navier–Stokes equations into the relevant Oseen equations. Since the flow around a sphere and circular cylinder for small Reynolds number may be considered a singular perturbation problem, it can be addressed using the method of matched asymptotic expansions, which begin with the full Navier–Stokes equations, and assuming appropriate inner expansions valid near the sphere or circular cylinder and outer expansions valid far from the sphere or circular cylinder. Following the terminology of Proudman and Pearson (4), Kaplun (5) and Van Dyke (6), the inner and outer expansions are termed the Stokes and Oseen expansions, respectively.
The above-mentioned analysis employs the no-slip boundary condition at the surface of the sphere and circular cylinder, that is, zero relative velocity is assumed between the fluid and solid, which is a fundamental notion in classical fluid mechanics (see for example Batchelor (7)). The microscopic origin of the no-slip boundary condition has remained elusive, and cannot be derived from first principles. As pointed out by Vinogradova (8), in most cases the no-slip boundary condition yields the correct results for simple flows, and experiments at macroscopic scales are consistent with the no-slip boundary condition. However, there exist both experimental and theoretical reasons for relaxing the no-slip hypothesis. In particular, experiments which probe molecular scales for which surface roughness may be of comparable magnitude indicate that the boundary condition at the surface of a solid may be different. An improved understanding of the effect of the fluid–solid interaction on flows at this scale is essential and has received a lot of attention (see for example Thompson and Robbins (9)).
Molecular dynamics studies by Qian et al. (10) have shown relative slipping between the fluid and the solid, in violation of the no-slip boundary condition. These findings cast doubt on the general applicability of the continuum hydrodynamics model of micro- and nanofluidics, where the boundary conditions may have macroscopic implications. Detailed studies of the fluid–solid interaction by Thompson and Troian (11) showed that the degree of slip depends on a number of interfacial parameters including unequal wall and fluid densities and the strength of the weak wall–fluid interaction. Together these effects prevent the locking of fluid layer(s) to the solid wall, thus allowing slip to occur (Qian and Wang (12)). Recent studies by Sokhan et al. (13, 14) of the fluid flow in carbon nanopores and nanotubes has shown it to be characterized by a large slip length.
Although the amount of slip depends on molecular details, Hocking (15) and Lamb (16) have suggested that the overall effect on the flow on a macroscopic scale can be obtained by postulating a dynamic boundary condition in which the relative velocity at the solid boundary is proportional to the tangential viscous stress there, that is, the net tangential force per unit area exerted on the solid due to the hydrodynamic motion of the surrounding fluid (10). The constant of proportionality which expresses the ratio of the relative velocity to the tangential viscous stress is termed the slip length, denoted by  (note that Lamb (16) refers to the slip length as the coefficient of sliding friction). As demonstrated by Qian and Wang (12), for a Newtonian fluid, the tangential viscous stress is proportional to the shear rate; consequently, the amount of slip is proportional to the shear rate. This linear slip–shear relation is the simplest known boundary condition used to improve the no-slip condition, with different expressions for the slip length due to different physical backgrounds (see for example Shikhmurzaev (17)). A linear slip condition frequently makes the problem tractable (Huh and Scriven (18)), and was first introduced by Navier in 1823 (19) and later independently by Maxwell in 1879 (20) (see Dussan (21) for a historical review). The so-called Navier boundary condition is applicable whenever the molecular mean free path approaches the dimensions of the flow (18). That is, for flows at the macro or nano scale, or when mathematical results predict an unrealistic stress divergence (see Hocking (15, 22) for an account of this usage), and when there exists surface roughness which may significantly affect the flow. Usually, such a change in the no-slip boundary would in most circumstances be undetectable, since the additional term would only change the macroscopic flow by an amount proportional to the ratio of the molecular to the macroscopic length scales.
(note that Lamb (16) refers to the slip length as the coefficient of sliding friction). As demonstrated by Qian and Wang (12), for a Newtonian fluid, the tangential viscous stress is proportional to the shear rate; consequently, the amount of slip is proportional to the shear rate. This linear slip–shear relation is the simplest known boundary condition used to improve the no-slip condition, with different expressions for the slip length due to different physical backgrounds (see for example Shikhmurzaev (17)). A linear slip condition frequently makes the problem tractable (Huh and Scriven (18)), and was first introduced by Navier in 1823 (19) and later independently by Maxwell in 1879 (20) (see Dussan (21) for a historical review). The so-called Navier boundary condition is applicable whenever the molecular mean free path approaches the dimensions of the flow (18). That is, for flows at the macro or nano scale, or when mathematical results predict an unrealistic stress divergence (see Hocking (15, 22) for an account of this usage), and when there exists surface roughness which may significantly affect the flow. Usually, such a change in the no-slip boundary would in most circumstances be undetectable, since the additional term would only change the macroscopic flow by an amount proportional to the ratio of the molecular to the macroscopic length scales.
The validity of the Navier boundary condition has been shown by Qian and Wang (12) for the driven cavity problem through molecular dynamic and continuum hydrodynamic simulation for a Newtonian fluid, where the no-slip boundary condition causes unphysical stress divergence. The slip length is determined from molecular dynamics simulations, usually ranging from one to a few nanometers, and when used as an input for the continuum hydrodynamic simulation it has been shown by Qian et al. (23, 24) that molecular dynamics results can be successfully reproduced. This and other work has shown that for flow at the micro or nano scale the no-slip boundary condition is not a valid postulate. We propose that a different postulate, namely the Navier boundary condition, may be a more accurate reflection of physical reality at a fluid/solid interface at micro or nano scales. The no-slip boundary condition is in fact an approximation to the Navier boundary condition, corresponding to  = 0. (The limit of infinite slip length corresponds to the conventional condition for a liquid/gas interface, that is perfect slip, as demonstrated in the analysis of film drainage by Vinogradova (8).) As the amount of slip is extremely small for macroscopic flows, the Navier boundary condition is practically indistinguishable from the no-slip condition in most cases on the macroscopic scale. In particular, Richardson (25) has shown that for a general Newtonian fluid flow in the immediate neighbourhood of a rough solid wall the no-slip boundary condition is the relevant macroscopic boundary condition, in the sense that deviations between the results for no-slip and infinite slip are of the order of the slip length. However, for micro or nano scale problems, the difference between the solutions for no-slip and infinite slip are of an order comparable to the dimensions of the flow, and that is the dimension of interest in this study.
= 0. (The limit of infinite slip length corresponds to the conventional condition for a liquid/gas interface, that is perfect slip, as demonstrated in the analysis of film drainage by Vinogradova (8).) As the amount of slip is extremely small for macroscopic flows, the Navier boundary condition is practically indistinguishable from the no-slip condition in most cases on the macroscopic scale. In particular, Richardson (25) has shown that for a general Newtonian fluid flow in the immediate neighbourhood of a rough solid wall the no-slip boundary condition is the relevant macroscopic boundary condition, in the sense that deviations between the results for no-slip and infinite slip are of the order of the slip length. However, for micro or nano scale problems, the difference between the solutions for no-slip and infinite slip are of an order comparable to the dimensions of the flow, and that is the dimension of interest in this study.
The Navier boundary condition assumes that the degree of slip is independent of the shear rate, that is  is constant, although recent molecular dynamic simulations by Thompson and Troian (11) have indicated that
is constant, although recent molecular dynamic simulations by Thompson and Troian (11) have indicated that  is a nonlinear function of the shear rate over a large range of shear rates. At low shear rates, the Navier boundary condition is valid, that is
is a nonlinear function of the shear rate over a large range of shear rates. At low shear rates, the Navier boundary condition is valid, that is  is constant, but at high shear rates the Navier boundary condition breaks down as
is constant, but at high shear rates the Navier boundary condition breaks down as  increases rapidly with the shear rate. Thus, the Navier boundary condition is a low-shear-rate limit of a more generalized universal relationship which is significantly nonlinear and divergent at a (high) critical shear rate. Modelling flows based on a functional dependence of the slip length on the tangential viscous stress would be inherently difficult, and possibly intractable analytically except for specific problems.
increases rapidly with the shear rate. Thus, the Navier boundary condition is a low-shear-rate limit of a more generalized universal relationship which is significantly nonlinear and divergent at a (high) critical shear rate. Modelling flows based on a functional dependence of the slip length on the tangential viscous stress would be inherently difficult, and possibly intractable analytically except for specific problems.
In this paper the linear Navier boundary condition with a constant slip length is applied to the steady flow of a Newtonian fluid past a nanosphere and a nanocylinder (or nanotube), a scale at which the slip length is relevant, using the method of matched asymptotic expansions. Since the phenomena of the motion of small particles depend critically on first-order effects arising from the inertia of the fluid as pointed out by Proudman and Pearson (4), the analysis is carried through to first order. The aim of the analysis is to determine the effect of a non-zero slip length on this most basic of flows, and to determine whether or not the Navier boundary condition may be employed to study more complicated flows at the nanoscale. In the following section, the equations describing the Navier boundary condition are presented. In sections 3 and 4 the analysis for the flow past a nanosphere and a nanocylinder are presented, and are subsequently solved using the method of matched asymptotic expansions with the Reynolds number assumed a small parameter. In section 5 some general features of the solutions obtained are discussed, as well as concluding remarks.
2 The Navier boundary condition
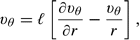
 is the slip length.
is the slip length.3 Flow past a nanosphere
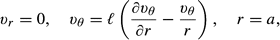
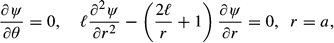
 * =
* =  /a the Navier–Stokes equation and boundary conditions become
/a the Navier–Stokes equation and boundary conditions become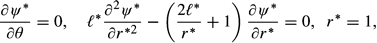
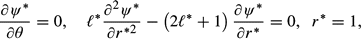
3.1 Leading-order expansions
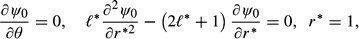
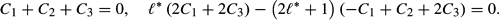
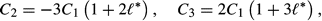
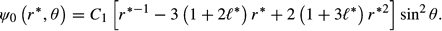
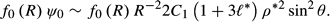
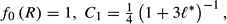
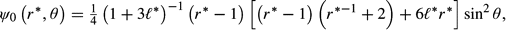
 * = 0 and agrees with the solution which appears in Basset (27) and Lamb (16).
* = 0 and agrees with the solution which appears in Basset (27) and Lamb (16).3.2 First-order expansions
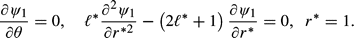
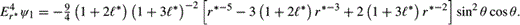
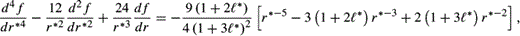
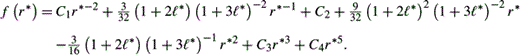
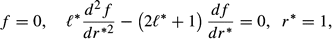
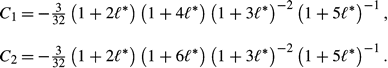
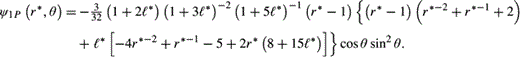
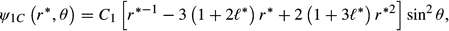
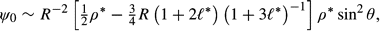
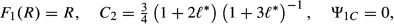
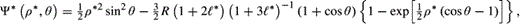
 * = 0.
* = 0.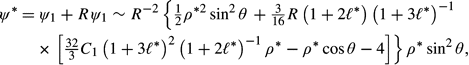
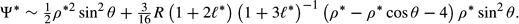
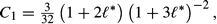
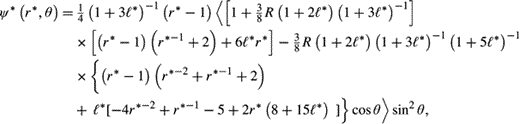
 * = 0.
* = 0.3.3 Frictional drag
There are two methods for calculating the frictional drag on a solid body immersed in a fluid—either the viscous stresses exerted by the fluid on the surface of the body are summed, or the theorem of momentum (or energy dissipation) is applied to an infinite mass of fluid surrounding the body, as mentioned by Tomotika and Aoi (28). Here the first method is used so that only the Stokes expansions and the relevant Navier–Stokes equation with assumptions consistent with the analysis are required to calculate the stresses, instead of a complementary solution of the Stokes and Oseen expansions and much more complicated form of the Navier–Stokes equation.
 *, which we keep dimensionless), substituting into the Navier–Stokes equations and integrating, yields the following expression for p evaluated at r = a:
*, which we keep dimensionless), substituting into the Navier–Stokes equations and integrating, yields the following expression for p evaluated at r = a: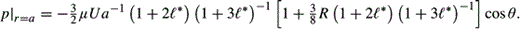
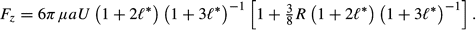
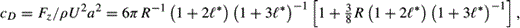
 * = 0, and agrees with the solution which appears in Basset (27) and Lamb (16) to leading order.
* = 0, and agrees with the solution which appears in Basset (27) and Lamb (16) to leading order.4 Flow past a nanocylinder
 * =
* =  /a the Navier–Stokes equation and boundary conditions become
/a the Navier–Stokes equation and boundary conditions become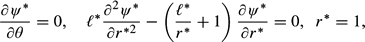
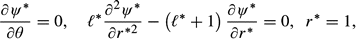
4.1 Leading-order expansions
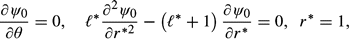
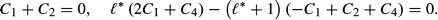
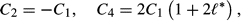
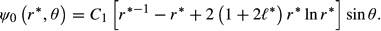
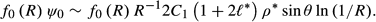
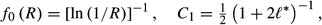
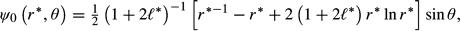
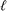 * = 0.
* = 0.4.2 First-order expansions
The first-order solution to the Stokes expansion satisfies the biharmonic equation
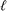 * = 0.
* = 0.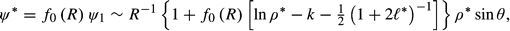
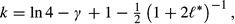
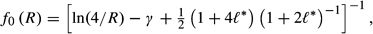
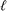 * = 0, and the full Stokes expansion is given by
* = 0, and the full Stokes expansion is given by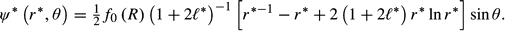
4.3 Frictional drag
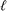 *, which we keep dimensionless), substituting into the Navier–Stokes equations and integrating yields the following expression for p evaluated at r = a:
*, which we keep dimensionless), substituting into the Navier–Stokes equations and integrating yields the following expression for p evaluated at r = a: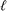 * = 0, where
* = 0, where 5 Numerical results and conclusions
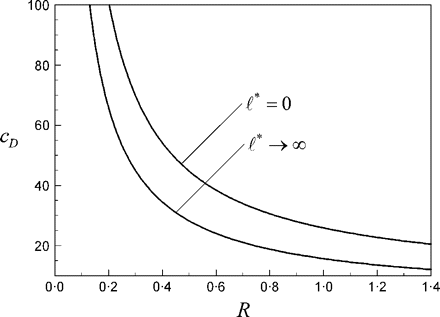
The expressions derived for the flow and the frictional drag on a nanosphere and nanocylinder, (3.1), (3.2), (4.3) and (4.4), may be discussed on the basis of the two extreme limits 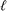 * = 0 and
* = 0 and 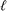 *→∞. The relevant results for finite
*→∞. The relevant results for finite 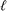 * will then fall between these two bounding curves.
* will then fall between these two bounding curves.
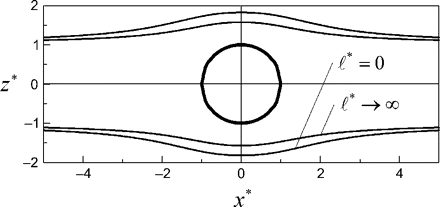
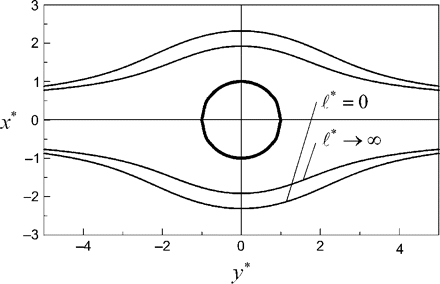
The flow past a nanosphere and nanocylinder are shown in Figs 1 and 3 for the case ψ* = 0·5 and R = 0·5 in the limits of 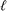 * = 0 and
* = 0 and 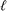 *→∞. These results show that the effect of slip has little effect on the streamlines of the flow, which move slightly closer to the nanosphere and nanocylinder for
*→∞. These results show that the effect of slip has little effect on the streamlines of the flow, which move slightly closer to the nanosphere and nanocylinder for 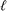 * > 0, indicating a reduced drag.
* > 0, indicating a reduced drag.
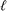 * > 0, since the fluid layers close to the nanosphere and nanocylinder would move across the corresponding surface with less resistance when slip is allowed. An important point to note is that, for the nanocylinder, the results for
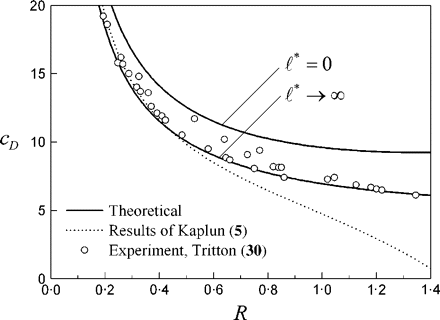
* > 0, since the fluid layers close to the nanosphere and nanocylinder would move across the corresponding surface with less resistance when slip is allowed. An important point to note is that, for the nanocylinder, the results for 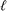 *→∞ for the frictional drag are in complete accord with the low-Reynolds-number experimental results of Tritton (30), and this agreement is much better than for
*→∞ for the frictional drag are in complete accord with the low-Reynolds-number experimental results of Tritton (30), and this agreement is much better than for 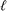 * = 0 and for the well-known higher approximation for the frictional drag obtained by Kaplun (5), which is given by
* = 0 and for the well-known higher approximation for the frictional drag obtained by Kaplun (5), which is given by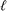 * = 0, which for comparison is also shown in Fig. 4. The excellent agreement with the experimental results of Tritton (30) in some part may be attributed to the micro diameter fibres used in the experiments, confirming the applicability of the approach adopted here at least at the micro scale.
* = 0, which for comparison is also shown in Fig. 4. The excellent agreement with the experimental results of Tritton (30) in some part may be attributed to the micro diameter fibres used in the experiments, confirming the applicability of the approach adopted here at least at the micro scale. Frictional drag versus Reynolds number for a nanocylinder with experimental points
In summary, the Newtonian flow past a nanosphere and a nanocylinder is modelled using matched asymptotic expansions. The classical no-slip boundary condition is replaced by the Navier boundary condition, which states that the relative velocity at a boundary is proportional to the tangential viscous stress at the boundary, and the constant of proportionality is the slip length 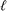 . Results for the streamlines and frictional drag are presented for
. Results for the streamlines and frictional drag are presented for 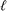 = 0 corresponding to classical theory, and
= 0 corresponding to classical theory, and 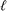 →∞ corresponding to complete slip. Numerical calculations reveal that the Navier boundary condition with a constant slip length has only a small effect on the response of both systems, implying that it only makes a small improvement over the classical no-slip boundary conditions for well-posed problems, that is, for problems that do not predict unrealistic divergence of any system response. The real advantages of using the Navier boundary condition as a replacement for the no-slip boundary condition arise when the former overcomes inherent failures of the latter, or when the slip length has a functional dependence on the shear rate.
→∞ corresponding to complete slip. Numerical calculations reveal that the Navier boundary condition with a constant slip length has only a small effect on the response of both systems, implying that it only makes a small improvement over the classical no-slip boundary conditions for well-posed problems, that is, for problems that do not predict unrealistic divergence of any system response. The real advantages of using the Navier boundary condition as a replacement for the no-slip boundary condition arise when the former overcomes inherent failures of the latter, or when the slip length has a functional dependence on the shear rate.
This work is funded by the Discovery Project scheme of the Australian Research Council, and the authors gratefully acknowledge this support.
References
G. G. Stokes, On the effect of the internal friction of fluids on the motion of pendulums,
A. N. Whitehead, Second approximations to viscous fluid motion,
I. Proudman and J. R. A. Pearson, Expansions at small Reynolds number for the flow past a sphere and circular cylinder,
O. I. Vinogradova, Drainage of a thin liquid film confined between hydrophobic surfaces,
P. A. Thompson and M. O. Robbins, Shear flow near solids: epitaxial order and flow boundary conditions,
T. Qian, X. P. Wang and P. Sheng, Generalized Navier boundary condition for the moving contact line,
P. A. Thompson and S. M. Troian, A general boundary condition for liquid flow at solid surfaces,
T. Qian and X. P. Wang, Driven cavity flow: from molecular dynamics to continuum hydrodynamics,
V. P. Sokhan, D. Nicholson and N. Quirke, Fluid flow in nanopores: accurate boundary conditions for carbon nanotubes,
V. P. Sokhan, D. Nicholson and N. Quirke, Fluid flow in nanopores: an examination of hydrodynamic boundary conditions,
Y. D. Shikhmurzaev, The moving contact line on a smooth solid surface,
C. Huh and L. E. Scriven, Hydrodynamic model of steady movement of a solid/liquid/fluid contact line,
C. L. M. H. Navier, Mémoire sur les lois du mouvement des fluides,
J. C. Maxwell, On stresses in rarefied gases arising from inequalities of temperature,
V. E. B. Dussan, On the spreading of liquids on solid surfaces: static and dynamic contact lines,
L. M. Hocking, A moving fluid interface. Part 2. the removal of the force singularity by a slip flow,
T. Qian, X. P. Wang and P. Sheng, Molecular scale contact line hydrodynamics of immiscible flows,
T. Qian, X. P. Wang and P. Sheng, Power-law slip profile of the moving contact line in two-phase immiscible flows,
S. Tomotika and T. Aoi, The steady flow of viscous fluid past a sphere and circular cylinder,