Skip to main content
SpringerLink
Log in

Modeling of Nonlinear Physiological Systems with Fast and Slow Dynamics. I. Methodology

  • Published:
Annals of Biomedical Engineering Aims and scope Submit manuscript

Abstract

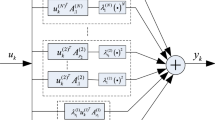
Effective modeling of nonlinear dynamic systems can be achieved by employing Laguerre expansions and feedforward artificial neural networks in the form of the Laguerre–Volterra network (LVN). This paper presents a different formulation of the LVN that can be employed to model nonlinear systems displaying complex dynamics effectively. This is achieved by using two different filter banks, instead of one as in the original definition of the LVN, in the input stage and selecting their structural parameters in an appropriate way. Results from simulated systems show that this method can yield accurate nonlinear models of Volterra systems, even when considerable noise is present, separating at the same time the fast from the slow components of these systems effectively. © 2002 Biomedical Engineering Society.

PAC2002: 8710+e, 0705Mh, 8718Sn, 0510Gg, 0210De

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. Alataris, K., T. W. Berger, and V. Z. Marmarelis. A novel network for nonlinear modeling of neural systems with arbitrary point-process inputs. Neural Networks 13:255–266, 2000.

    Google Scholar 

  2. Amorocho, J., and A. Brandstetter. Determination of nonlinear functional response functions in rainfall runoff processes. Water Resour. Res. 7:1087–1101, 1971.

    Google Scholar 

  3. Haykin, S. Neural Networks, A Comprehensive Foundation. Upper Saddle, NJ: Prentice-Hall, 1998.

    Google Scholar 

  4. Lee, Y. W., and M. Schetzen. Measurement of the Wiener kernels of a nonlinear system by cross-correlation. Int. J. Control 2:237–254, 1965.

    Google Scholar 

  5. Marmarelis, V. Z. Identification of nonlinear biological systems using Laguerre expansions of kernels. Ann. Biomed. Eng. 21:573–589, 1993.

    Google Scholar 

  6. Marmarelis, V. Z. Wiener analysis of nonlinear feedback in sensory systems. Ann. Biomed. Eng. 19:345–382, 1991.

    Google Scholar 

  7. Marmarelis, V. Z., and X. Zhao. Volterra models and three-layer perceptrons. IEEE Trans. Neural Netw. 8:1421–1433, 1997.

    Google Scholar 

  8. Ogura, H. Estimation of Wiener kernels of a nonlinear system and a fast algorithm using digital Laguerre filters. 15th NIBB Conference, Okazaki, Japan, 1985, pp. 14–62.

  9. Rissanen, J. Information theory and neural nets. In: Mathematical Perspectives on Neural Networks, edited by P. Smolensky, M. C. Mozer, and D. E. Rumelhart. Mahwah, NJ: Lawrence Erlbaum, 1996, pp. 567–602.

    Google Scholar 

  10. Watanabe, A., and L. Stark. Kernel method for nonlinear analysis: Identification of a biological control system. Math. Biosci. 27:99–108, 1975.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Biomedical Engineering, University of Southern California, University Park, Los Angeles, CA

    G. D. Mitsis & V. Z. Marmarelis

Authors
  1. G. D. Mitsis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. Z. Marmarelis
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mitsis, G.D., Marmarelis, V.Z. Modeling of Nonlinear Physiological Systems with Fast and Slow Dynamics. I. Methodology. Annals of Biomedical Engineering 30, 272–281 (2002). https://doi.org/10.1114/1.1458591

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1114/1.1458591

Search

Navigation