Review

The main objective of the present inspection is to study the MHD flow and radiative heat transfer of hyperbolic tangent fluid over a stretching sheet with fluid-particle suspension. The method of solution involves similarity transformation which reduces the partial differential equations into a non-linear ordinary differential equation. These non-linear ordinary differential equations have been solved by applying Runge-Kutta-Fehlberg forth-fifth order method (RKF45 Method) with help of Shooting technique. The temperature and velocity profiles for various values of flow parameters are presented in the figures. The numerical results of present investigation were compared with existing results and are found to be in good agreement.

Introduction

Boundary layer flow and heat transfer under the influence of stretching surface has received considerable attention in recent years. The problem has scientific and chemical engineering applications such as aerodynamic extrusion of plastic sheets and fibers, tinning of copper wire, drawing, crystal growing and glass blowing, annealing and paper production, metallurgical process, polymer extrusion process, continuous stretching, drawing, annealing and tinning of copper wires. Sakiadis (1961) was the pioneer of studying the boundary layer flow over a stretched surface moving under a constant velocity. Rajagopal and Gupta (1987) examined the boundary layer flow over a stretching sheet for a various class of non-Newtonian fluids. Rauta and Mishra (2014) investigated the heat transfer characteristics of two-dimensional flow in a porous medium over a stretching sheet with internal heat generation. Thereafter, exhaustive amount of researches were made related to boundary layer flow and heat transfer (see Ishak (2010), Ali (2006) and Yao et al. (2011)).

In recent years, many researchers are concentrated on the area of dusty fluid due to its wide range of applications such as fluidization, centrifugal separation of matter from fluid, purification of crude oil, dust collection, petroleum industry, powder technology, nuclear reactor cooling, performance of solid fuel rocket nozzles, and paint spraying. Saffman (1962) analyzed the flow of a dusty gas in which the fluid suspension particles are uniformly distributed. Further, Mohan Krishna et al. (2013) have discussed the flow of a dusty viscous fluid in the presence of transverse magnetic field with first order chemical reaction. Datta and Mishra (1982) presented the boundary layer flow of a dusty fluid over a semi-infinite flat plate along with the drag force. Due to these applications, a number of theoretical and experimental studies have been carried out by numerous researchers on dusty fluid (see (Palani and Ganesan 2007; Ramesh et al. 2017; Kumar et al. 2017a, 2017d, 2017f; Makinde et al. 2017)).

On the other hand, non-Newtonian fluids are found in many industrial and engineering processes, such as food mixing, flow of blood, plasma, mercury amalgams, and lubrications with heavy oils and greases. In view of these applications, many studies are focused on non-Newtonian fluid. Govardhan et al. (2015) initiated the magnetohydrodynamics flow of an incompressible micropolar fluid over a stretching sheet for unsteady case. Hayat et al. (2010) have initiated the effect of thermal radiation on a two-dimensional stagnation-point flow and heat transfer of an incompressible magneto-hydrodynamic Carreau fluid towards a shrinking surface with convective boundary condition. In modern days, all such interesting applications have motivated scientists and researchers to look for more avenues in the field of non-Newtonian flow (Rudraswamy et al. 2017a, 2017b; Kumar et al. 2017c, 2017e).

One of the imperative branches of non-Newtonian fluid is the tangent hyperbolic fluid capable of describing the shear thinning effects. Recently, Akbar et al. (2013) have discussed the two dimensional tangent hyperbolic fluid flow over a stretching in the presence of magnetic field. Malik et al. (2015) have used Keller box method to study MHD flow of tangent hyperbolic fluid under the influence of stretching cylinder. Nadeem and Akram (2011) analyzed the magnetohydrodynamics (MHD) peristaltic flow of a tangent hyperbolic fluid model in a vertical asymmetric channel (Fig. 1). Recently Naseer et al. (2014) have analyzed the steady boundary layer flow and heat transfer of a tangent hyperbolic fluid flow under the influence of vertical exponentially stretching cylinder. Kumar et al. (2017b) discussed an unsteady squeezed flow of a tangent hyperbolic fluid over a sensor surface in the presence of variable thermal conductivity. Nadeem and Maraj (2013) initiated the mathematical analysis for peristaltic flow of tangent hyperbolic fluid in a curved channel.

The main objective of the present inspection is to study the MHD flow and radiative heat transfer of hyperbolic tangent fluid over a stretching sheet with fluid-particle suspension. The method of solution involves similarity transformation which reduces the partial differential equations into a non-linear ordinary differential equation. These non-linear ordinary differential equations have been solved by applying Runge–Kutta–Fehlberg fourth-fifth order method (RKF-45 Method) with the help of shooting technique. The temperature and velocity profiles for various values of flow parameters are presented in the figures. The numerical results of present investigation were compared with existing results and are found to be in good agreement.

Method

The system of non-linear ordinary differential equations (2.8)–(2.9) and (3.10)–(3.11) using the boundary conditions (2.10) and (3.12) are solved numerically using Runge–Kutta–Fehlberg fourth-fifth (RKF-45) method. In maple, two sub methods are available, namely trapezoidal and midpoint method. To solve this kind of two-point boundary value problem the trapezoidal method is generally efficient, but it is incapable to handle harmless endpoint singularities, but this can be able in midpoint method. Thus, the mid-point method with the Richardson extrapolation enhancement scheme is chosen as a sub method. The asymptotic boundary conditions at η∞ were replaced by those at η∞ = 6 in accordance with standard practice in the boundary layer analysis. Additionally, the relative error tolerance for convergence is considered to be 10−6 throughout our numerical computations. The consequences of assorted pertinent parameters on flow and heat transfer characteristics are mentioned numerically and presented graphically. Comparisons between the current and former limiting results were shown in the Tables 1 and 2.

Table 1 Comparison table of skin friction coefficient (We = n = 0)
Full size table
Table 2 Comparison of −θ′(0) for different values of Prandtl number (Pr) when M = 0, We = 0, n = 0, Ec = 0, and R = 0
Full size table

Mathematical formulation

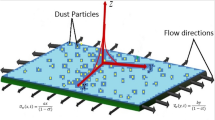
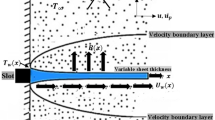
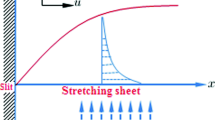
Let us consider a steady flow of an incompressible hyperbolic tangent fluid over a stretching sheet. The flow is assumed to be confined to region of y > 0. The flow is generated by the action of two equal and opposite forces along the x-axis and y-axis being normal to the flow. A uniform magnetic field B0 is imposed along the y-axis and the sheet being stretched with the velocity u w (x) along the x-axis. The number density is assumed to be constant and volume fraction of dust particles is neglected. The fluid and dust particle motions are coupled only through drag and heat transfer between them. The drag force is modeled using Stokes linear drag theory. Other interaction forces such as the virtual force, the shear lift force, and the spin-lift force will be neglected compared to the drag force. The term T w represents the temperature of fluid at the sheet, whereas T∞ denotes the ambient fluid temperature.

The constitutive equation of tangent hyperbolic fluid is (Akbar et al. 2013)

$$ \overline{\tau}=\left[{\mu}_0+\left({\mu}_0+{\mu}_{\infty}\right)\tanh {\left(\Gamma \overline{\dot{\gamma}}\right)}^n\right]\overline{\dot{\gamma}}, $$
(2.1)

in which, \( \overline{\tau} \) is the extra stress tensor, μ∞ the infinite shear rate viscosity, μ0 the zero shear rate viscosity, Γ is the time dependent material constant, n the power law index, i.e., flow behavior index and \( \overline{\dot{\gamma}} \) is defined as

$$ \overline{\dot{\gamma}}=\frac{1}{2}\sqrt{\frac{1}{2}{\sum}_i{\sum}_j{\overline{\dot{\gamma}}}_{ij}{\overline{\dot{\gamma}}}_{\mathrm{ji}}}=\sqrt{\frac{1}{2}\Pi}. $$

Consider Eq. (2.1), for the case when μ∞ = 0, because it is not possible to discuss the problem for infinite shear rate viscosity and since we have considered tangent hyperbolic fluid that describing shear thinning effects so \( \Gamma \overline{\dot{\gamma}}<1 \). Then, Eq. (2.1) takes the form

$$ {\displaystyle \begin{array}{c}\overline{\tau}={\mu}_0\left[{\left(\Gamma \overline{\dot{\gamma}}\right)}^n\right],\\ {}={\mu}_0\left[1+n\left(\Gamma \overline{\dot{\gamma}}-1\right)\right]\overline{\dot{\gamma}}.\end{array}} $$

Governing equations for hyperbolic tangent fluid model after applying the boundary layer approximations can be defined as follows (Hayat et al. 2010; Rudraswamy et al. 2017a):

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, $$
(2.2)
$$ u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \left(1-n\right)\frac{\partial^2u}{\partial {y}^2}+\sqrt{2}\nu n\Gamma \left(\frac{\partial u}{\partial y}\right)\frac{\partial^2u}{\partial {y}^2}+\frac{KN}{\rho}\left({u}_p-u\right)-\frac{\sigma {B}_0^2}{\rho }u, $$
(2.3)
$$ \frac{\partial {u}_p}{\partial x}+\frac{\partial {v}_p}{\partial y}=0, $$
(2.4)
$$ {\rho}_p\left({u}_p\frac{\partial {u}_p}{\partial x}+{v}_p\frac{\partial {u}_p}{\partial y}\right)= KN\left(u-{u}_p\right), $$
(2.5)

where (u, u p ) and (v, v p ) are the velocity components in x and y directions of the fluid and dust particle phase, respectively. ρ and ρ p  = mN are the densities of the fluid and dust particle phase, respectively. m and N are the mass and number density of the dust particles per unit volume, respectively. σ is the electrical conductivity of the fluid, ν is the kinematic viscosity of the base fluid, μ is the coefficient of viscosity of the fluid, K = 6πμr is the Stokes drag coefficient, and r is the radius of dust particle.

The appropriate boundary conditions applicable to the present problem are

$$ {\displaystyle \begin{array}{l}u={u}_w(x),\kern0.5em v=0\kern0.75em \mathrm{at}\;y=0,\\ {}u\to 0,\kern0.5em {u}_p\to 0,\kern0.5em {v}_p\to v\;\mathrm{as}\;y\to \infty, \end{array}} $$
(2.6)

where u w (x) = bx is a stretching sheet velocity with b (>0) as the stretching rate.

Equations (2.2) to (2.5) subjected to boundary conditions (2.6) admits self-similar solution in terms of the similarity function f, F and similarity variable η and they are defined as

$$ {\displaystyle \begin{array}{l}u= bx{f}^{\prime}\left(\eta \right),\kern0.5em v=-\sqrt{\nu b}f\left(\eta \right),\eta =\sqrt{\frac{b}{v}}y,\\ {}\begin{array}{ll}{u}_p= bx{F}^{\prime}\left(\eta \right),& {v}_p=-\sqrt{\nu b}F\left(\eta \right),\end{array}\end{array}} $$
(2.7)

the Eq. (2.2) and (2.4) are identically satisfied, in terms of relations (2.7). In addition, the equation (2.3) and (2.5) are reduced to the following set of non-linear ordinary differential equations:

$$ {\displaystyle \begin{array}{c}\left(1-n\right){f}^{\prime \prime \prime}\left(\eta \right)-{\left[{f}^{\prime}\left(\eta \right)\right]}^2+{f}^{\prime \prime}\left(\eta \right)f\left(\eta \right)+n{W}_e{f}^{\prime \prime \prime}\left(\eta \right){f}^{\prime \prime}\left(\eta \right)+l{\beta}_v\left[{F}^{\prime}\left(\eta \right)-{f}^{\prime}\left(\eta \right)\right]\\ {}-M\kern0.28em {f}^{\prime}\left(\eta \right)=0,\end{array}} $$
(2.8)
$$ F\left(\eta \right){F}^{\prime \prime}\left(\eta \right)-{\left[{F}^{\prime}\left(\eta \right)\right]}^2+{\beta}_v\left[\kern0.5em {f}^{\prime}\left(\eta \right)-{F}^{\prime}\left(\eta \right)\right]=0. $$
(2.9)

Transformed boundary conditions are

$$ {\displaystyle \begin{array}{l}{f}^{\prime }=1,\kern0.5em \begin{array}{cc}f\left(\eta \right)=0& \mathrm{at}\;\eta =0,\end{array}\\ {}\begin{array}{ccc}{f}^{\prime}\left(\eta \right)\to 0& {F}^{\prime}\left(\eta \right)\to 0,& F\left(\eta \right)\to f\left(\eta \right)\;\mathrm{as}\;\eta \to \infty, \end{array}\end{array}} $$
(2.10)

where \( l=\frac{Nm}{\rho } \) is the mass concentration parameter of dust particles, \( M=\frac{\sigma {B}_o^2}{\rho b} \) is the magnetic parameter, \( {\tau}_v=\frac{m}{K} \) is the relaxation time of the dust particles, \( {\beta}_v=\frac{1}{b{\tau}_v} \) is the fluid-particle interaction parameter for velocity, \( {W}_e=\frac{\sqrt{2b}{\Gamma u}_w}{\sqrt{\nu }} \) is the Weissenberg number, and n is the power law index parameter.

Heat transfer analysis

The governing boundary layer heat transport equations for both fluid and dust phase are given by

$$ {c}_p\rho \left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k\frac{\partial^2T}{\partial {y}^2}+\frac{\rho_{p{C}_p}}{\tau_T}\left({T}_p-T\right)+\frac{\rho_p}{\tau_v}{\left({u}_p-u\right)}^2-\frac{\partial {q}_r}{\partial y}, $$
(3.1)
$$ {u}_p\frac{\partial {T}_p}{\partial x}+{v}_p\frac{\partial {T}_p}{\partial y}=-\frac{c_p}{c_m{\tau}_T}\left({T}_p-\mathrm{T}\right), $$
(3.2)

where T and T p are the temperature of the fluid and dust particles, respectively, c p and c m are the specific heat of fluid and dust particles, respectively, τ T is the thermal equilibrium time, i.e., the time required by the dust cloud to adjust its temperature to that of fluid, k is the thermal conductivity of the fluid, and q r is the radiative heat flux.

Using the Rosseland approximation for radiation, radiation heat flux is simplified as

$$ {q}_r=-\frac{4{\sigma}^{\ast }}{3{k}^{\ast }}\frac{\partial {T}^4}{\partial y}, $$
(3.3)

where σ∗ is the Stefan–Boltzmann constant and k∗ is the mean absorption coefficient. It is noted that the optically thick radiation limit is considered in this model. Assuming that the temperature differences within the flow are sufficiently small such that T4 may be expressed as a linear function of temperature, we expand T4 in a Tayler series about T∞ as follows:

$$ {T}^4={T}_{\infty}^4+4{T}_{\infty}^3\left(\ T-{T}_{\infty}\right)+6{T}_{\infty}^2{\left(\ T-{T}_{\infty}\right)}^2+\dots, $$
(3.4)

neglect the higher order terms beyond the first degree in ( T − T∞), one can get,

$$ {T}^4\cong 4{T}_{\infty}^3T-3\ {T}_{\infty}^4. $$
(3.5)

Substituting Eq. (3.5) in Eq. (3.3) one can get,

$$ \frac{\partial {q}_r}{\partial y} = -\frac{16{\sigma}^{\ast }{T}_{\infty}^3}{3{k}^{\ast }}\frac{\partial^2T}{\partial {y}^2}. $$
(3.6)

In view of the Eq. (3.6), the energy Eq. (3.1) becomes

$$ {c}_p\rho \left(u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}\right)=\left(k+\frac{16{\sigma}^{\ast }{T}_{\infty}^3}{3{k}^{\ast }}\right)\frac{\partial^2T}{\partial {y}^2}+\frac{\rho_{p{C}_p}}{\tau_T}\left({T}_p-T\right)+\frac{\rho_p}{\tau_v}{\left({u}_p-u\right)}^2. $$
(3.7)

Corresponding boundary conditions for the temperature are considered as follows:

$$ {\displaystyle \begin{array}{l}T={T}_w\kern0.5em \mathrm{at}\kern0.5em y=0\\ {}\begin{array}{ccc}T\to {T}_{\infty },& {T}_p\to {T}_{\infty}\;\mathrm{as}& y\to \infty \end{array}\end{array}} $$
(3.8)

The dimensional fluid phase temperature θ(η) and dust phase temperature θ p (η) are defined as

$$ \theta \left(\eta \right)=\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }},\kern1em {\theta}_p\left(\eta \right)=\frac{T_p-{T}_{\infty }}{T_w-{T}_{\infty }}. $$
(3.9)

Using (3.9) into (3.7) and (3.2), one can get the following non-linear ordinary differential equations:

$$ \left(1+\frac{4}{3}R\right){\theta}^{{\prime\prime}}\left(\eta \right)+\Pr {\theta}^{\prime}\left(\eta \right)f\left(\eta \right)+ lPr{\beta}_t\left({\theta}_p\left(\eta \right)-\theta \left(\eta \right)\right)+{\beta}_vl\;\mathrm{EcPr}{\left[\ {F}^{\prime}\left(\eta \right)-{f}^{\prime}\left(\eta \right)\right]}^2=0, $$
(3.10)
$$ {\theta}_p^{\prime}\left(\eta \right)F\ \left(\eta \right)-\gamma {\beta}_t\left[{\theta}_p\left(\eta \right)-\theta \left(\eta \right)\right]=0, $$
(3.11)

with

$$ {\displaystyle \begin{array}{l}\theta \left(\eta \right)=1\;\mathrm{at}\kern0.5em \eta =0,\\ {}\begin{array}{ccc}\theta \left(\eta \right)\to 0,& {\theta}_p\left(\eta \right)\to 0& as\;\eta \to \infty, \end{array}\end{array}} $$
(3.12)

where \( \Pr =\frac{\mu {C}_p}{k} \) is Prandtl number, the prime denote differentiation with respect to η and \( R=\frac{4{\sigma}^{\ast }{T}_{\infty}^3}{k^{\ast }k} \) is the radiation parameter, \( \mathrm{Ec}=\frac{u_w^2}{c_p\left({T}_w-{T}_{\infty}\right)} \) is the Eckert number, \( \gamma =\frac{c_p}{c_m} \) is the specific heat ratio, \( {\beta}_t=\frac{1}{b{\tau}_T} \) is the fluid-particle interaction parameter for temperature.

The physical quantities of interest like skin friction coefficient (C f ) and local Nusselt number (Nu x ) are defined as

$$ {c}_f=\frac{\tau_w}{\rho {u}_w^2}\;\mathrm{and}\;{\mathrm{Nu}}_x=\frac{u_w{q}_w}{ak\left({T}_{\infty }-{T}_w\right)} $$

where the shear stress (τ w ) and surface heat flux (q w ) are given by

$$ {\tau}_w={\mu}_0\left(\left(1-n\right)\frac{\partial u}{\partial y}+\frac{n\Gamma}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right)\kern0.37em \mathrm{and}\;{q}_w=-k\ \frac{\partial T}{\partial y}+{q}_r. $$

Using the non-dimensional variables, one can get

$$ \sqrt{\mathit{\operatorname{Re}}}{C}_f={\left[\left(1-n\right){f}^{{\prime\prime}}\left(\eta \right)+\frac{n}{2}{W}_e{\left({f}^{{\prime\prime}}\left(\eta \right)\right)}^2\right]}_{\eta =0}\;\mathrm{and}\;\frac{{\mathrm{Nu}}_x}{\sqrt{{\operatorname{Re}}_x}}=-\left(1+\frac{4}{3}R\right)\ {\theta}^{\prime }(0), $$
(3.14)

where \( \mathrm{R}{\mathrm{e}}_x=\frac{u_w^2}{a\nu} \) is the local Reynold’s number.

Result and discussion

In the current paper, we have investigated the impact of thermal radiation on the boundary layer flow of dusty hyperbolic tangent fluid over a stretching sheet with applied magnetic field. The velocity and temperature profile for each fluid and dust phase are aforethought to research the influence of assorted flow dominant parameters like magnetic parameter, Prandtl number, Eckert number, specific heat ratio, Weissenberg number, thermal radiation parameter, power law index, and fluid-particle interaction parameter. The numerical values for skin friction coefficient and Nusselt number are maintained in Tables 3 and 4. The numerical results of a present investigation are compared with previous published results and located to be sensible agreement as shown in Tables 1 and 2.

Table 3 Numerical values of \( -\sqrt{\operatorname{Re}}{C}_f \) and \( -\left[\frac{\mathrm{N}{\mathrm{u}}_x}{\mathrm{R}{\mathrm{e}}^{1/2}}\right] \) for different values of We, n, M, β v , and l
Full size table
Table 4 Numerical values of \( -\left[\frac{\mathrm{N}{\mathrm{u}}_x}{\mathrm{R}{\mathrm{e}}^{1/2}}\right] \) for different values of Ec, γ, Pr , R, and β t
Full size table

Figure 2a, b describes the impact of Weissenberg number (We) over the velocity and temperature profile. Weissenberg number is the quantitative relation of the relaxation time of the fluid and a particular process time. This ratio will increase the thickness of the fluid, thus, velocity profile and also the associated boundary layer thickness decreases with increase of W e in shown in Fig. 2a. In the case of the temperature profile, it exhibits the opposite behavior of velocity profile as in Fig. 2b.

Fig. 1
figure 1

Physical model of the flow and coordinate system

Full size image

Figure 3a, b depicts the behavior of power law index (n) on velocity and temperature profile. Figure 3a exposes that the velocity profile and corresponding boundary layer thickness decreases by increasing the values of power law index parameter (n). Figure 3b emphasizes the temperature distribution for various values of power law index parameter. From this figure, temperature profile is strongly depressed with increasing power law index.

Fig. 2
figure 2

a, b Velocity profile and temperature profile for different values of We

Full size image

The velocity and temperature profiles are pictured in Fig. 4a, b for the variation of a magnetic parameter (M). In general, an application of transverse magnetic field normal to the flow of an electrically conducting fluid has the affection to yield a drag-like force called the Lorentz force, which acts in the direction opposite to that of flow, thus reducing its velocity. The results also show that momentum boundary layer thickness decreases whereas thermal boundary layer thickness increases.

Fig. 3
figure 3

a, b Velocity profile and temperature profile for different values of n

Full size image

The variations of velocity and temperature profile for both the phases are illustrated in Fig. 5a, b for various values of β v and β t . An uplifting value of β v can decrease the fluid phase velocity and will increase the dust phase velocity. While, evidently, an increase in β t can increase the dust phase and reduce the fluid phase temperature profile. This is because of the presence of dust particles produces friction force in the fluid, which retards the flow.

Fig. 4
figure 4

a, b Velocity profile and temperature profile for different values of M

Full size image

Figure 6a, b shows the impact of l on velocity and temperature profiles for each fluid and particle phases. Once the dust particles are suspended within the clean fluid, an interior friction is created at intervals in the fluid, and additionally, the dust particles absorb heat from the fluid once they acquire contact. As a result, thinning of thermal boundary layer thickness takes place. This tends to scale back the velocity and temperature profiles of both phases with the increase in dust particle parameter.

Fig. 5
figure 5

a, b Velocity profile and temperature profile for different values of β v and β t

Full size image

Figures 7a, 7b, and 8a depict the temperature profiles for various values of Eckert number (Ec), specific heat ratio (γ), and radiation parameter (R), respectively. One can infer from these figures that the temperature and thickness of the corresponding boundary layer of both phases will increase with rising in Ec, γ, and R. Here, Fig. 8a, determines that the effect of radiation is also to enhance the heat transfer. Thus, radiation should be at its minimum in order to facilitate the cooling process. Figure 8b describes the impact of Prandtl number (Pr) over the temperature profile. Hear the thermal boundary layer thickness minimizes by maximizing the values of Prandtl number. The central reason for reduction in temperature is a higher Prandtl number has relatively low thermal conductivity, which causes low heat penetration, thus the thermal boundary layer thickness of fluid and dust particles decreases with the rise in Prandtl number.

Fig. 6
figure 6

a, b Velocity profile and temperature profile for different values of l

Full size image
Fig. 7
figure 7

a and b Temperature profiles for different values of Ec and γ, respectively

Full size image

Figure 9a–c depicts the skin friction coefficient for β v , n, and We with different values of l, M, and l, respectively. It is obvious that skin friction coefficient will increase with associate rising values of β v , n, and We versus l, M, and l, respectively. In Fig. 10a, b, it determined that the Nusselt number decrease with increasing values of γ and R versus Ec and γ, respectively. However, Nusselt number while increase by increasing the values of Pr and β t versus R and l, respectively. This is shown in Fig. 10c, d.

Fig. 8
figure 8

a and b Temperature profiles for different values of R and Pr, respectively

Full size image
Fig. 9
figure 9

a Influence of β v and l on skin friction. b Influence of n and M on skin friction. c Influence of n and M on skin friction

Full size image
Fig. 10
figure 10

a Influence of Ec and γ on Nusselt number. b Influence of R and γ on Nusselt number. c Influence of R and Pr on Nusselt number. d Influence of l and β t on Nusselt number

Full size image

Table 3 presents the numerical values of Nusselt number and skin friction coefficient for various values M, We, β v . It is observed that skin friction increase and Nusselt number decreases with increasing M, We, β v , l, and n. Table 4 presents the numerical values of local Nusselt number for various values Ec, γ, Pr , R, and β t . From this table, we observed that, Nusselt number increase with an increasing the values of Pr and β t whereas an opposite trend is observed for different values Ec, γ, and R.

Conclusions

The present work includes the impact of thermal radiation on boundary layer flow of dusty hyperbolic tangent fluid over a stretching sheet underneath the influence of magnetic field. Numerical results are conferred in tabular/graphical kind to elucidate the details of flow and heat transfer characteristics and their dependence on the varied physical parameters. The subsequent conclusions are drawn:

  • Increasing values of W e and n will increase the temperature profile. However, decrease the velocity profile.

  • An increasing values of Ec, γ, and R parameters increase the thermal boundary layer thickness.

  • The temperature profile and corresponding boundary layer thickness was depressed by uplifting the Prandtl number.

  • Velocity and temperature profiles decreases by an increasing values of l.

  • With a rise of β v and β t , velocity and temperature profile decreases for fluid phase, but increases for dust phase.

  • An increase in the thermal boundary layer thickness and decrease in momentum boundary layer thickness was observed for the increasing values of the magnetic parameter M.

Nomenclature

\( {B}_0^2 \) magnetic field

b stretching rate

c p fluid phase specific heat coefficient (J/kgK)

c m dust phase specific heat coefficient (J/kgK)

C f skin friction coefficient

Ec Eckert number

f dimensionless velocity of the fluid phase

F dimensionless velocity of the dust phase

K Stokes drag constant

k thermal conductivity

k∗ mean absorption coefficient (m−1)

l mass concentration of dust particles parameter

M magnetic parameter

m mass of dust particles

n power law index

N dust particles number density

Nu x local Nusselt number

Pr Prandtl number

q w heat flux at the surface

q r radiative heat flux (Wm−2 )

R radiation parameter

r radius of dust particles

Re x local Reynolds number

Sh x Sherwood number

T temperature of the fluid phase

T p temperature of the dust phase

T w temperature of the fluid at the sheet

T∞ ambient fluid temperature

u w stretching sheet velocity

u, u p velocity components of fluid phase

v, v p velocity components of dust phase

We Weissenberg number

x coordinate along the plate (m)

y coordinate normal to the plate (m)

Greek symbols

β v fluid-particle interaction parameter for velocity

β t fluid-particle interaction parameter for temperature

μ dynamic viscosity (kgm−1s−1 )

ν kinematic viscosity

σ electrical conductivity of the fluid

σ∗ Stefan-Boltzmann constant

θ temperature of the fluid phase

θ p temperature of the dust phase

η similarity variable

τ T thermal equilibrium time

τ w surface shear stress

τ v dust particles relaxation time

γ specific heat ratio

ρ base fluid density (kg/m3 )

ρ p dust particles density

Γ the time constant

Superscript:

′ derivative with respect to η

Subscript:

p particle phase

∞ fluid properties at ambient condition.