Abstract
The anomalous Hall conductivity (AHC) in some ferromagnetic and antiferromagnetic Heusler compounds was theoretically and experimentally found to be exceptionally large. For the case of ferromagnetic Co2MnAl we here argue that the large AHC is connected with the appearance of Weyl points near the Fermi energy. We find four Weyl points slightly above the Fermi edge. We describe our analysis for a magnetization being in the (110)-direction. For the possible (100)-direction we find at least four Weyl points, too. We predict that Co2MnGa also possesses Weyl points near or at the Fermi energy.
Export citation and abstract BibTeX RIS
Introduction
The study of the anomalous Hall effect (AHE) has recently been attracting a growing amount of attention. Its basic theory and the connection with a topological property, the Berry phase, has been reviewed in great detail [1,2], and its application to ferromagnetic compounds, also of the Heusler type, has appeared in ref. [3–6]. Furthermore, a large anomalous Hall conductivity (AHC) was predicted and very recently discovered experimentally in non-collinear antiferromagnetic compounds [7–10].
An interesting question that comes up in connection with the exceptional values of the AHC in some ferromagnets [3] and in the antiferromagnets concerns a possible mechanism for the large size of the AHC. Here we believe there is a connection with another growing field, namely the discovery of Weyl fermions in semimetals [11–13]. Of special interest is a proposal by Wang et al. who predict and see Weyl points in some magnetic Heusler compounds [14].
The original concept of Weyl fermions comes from the standard model, where Weyl fermions are predicted to exist, but are not found experimentally. In condensed matter physics Weyl points appear when non-degenerate energy bands cross near or at the Fermi energy. They give rise to a singularity in the Berry curvature or a "magnetic monopole" in momentum space. They come in pairs and produce surface disconnected Fermi arcs, first predicted by Wan et al. [11].
Heusler compounds are face-centered cubic metallic compounds with space-group symmetry Fm-3m (No. 225 International Tables). Co2MnAl is a ferromagnet with a magnetic moment of  p.f.u., a Curie temperature of 697 K, 75% spin polarization at the Fermi energy and an AHC of
p.f.u., a Curie temperature of 697 K, 75% spin polarization at the Fermi energy and an AHC of 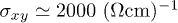 [3,6,15].
[3,6,15].
The calculations
The anomalous Hall effect is obtained by computing the Berry curvature in momentum space. This is a vector, writing its p-component as  , and is obtained from the curl of the Berry connection given by
, and is obtained from the curl of the Berry connection given by 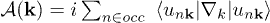 , where
, where  is the crystal-periodic eigenfunction having wave vector k and band index n. The sum extends over the occupied states. For its evaluation we use the wave functions from density functional calculations [16] following ref. [3], where the numerical work is based on
is the crystal-periodic eigenfunction having wave vector k and band index n. The sum extends over the occupied states. For its evaluation we use the wave functions from density functional calculations [16] following ref. [3], where the numerical work is based on ![$\Im \ln\det[\langle u_{n \bf k}|u_{m \bf k'}\rangle]$](https://content.cld.iop.org/journals/0295-5075/114/4/47005/revision1/epl17881ieqn6.gif) , which is directly related to the Berry connection [17]. Spin-orbit coupling (SOC) is treated in second variation and is an essential ingredient. The Hall conductivity follows from the Berry curvature by means of
, which is directly related to the Berry connection [17]. Spin-orbit coupling (SOC) is treated in second variation and is an essential ingredient. The Hall conductivity follows from the Berry curvature by means of

where  is the Fermi distribution function,
is the Fermi distribution function,  is the p-component of the Berry curvature for the wave-vector k and the components ℓ, m, p are to be chosen cyclic [2]. A limit to our numerical procedure is the rather high number of k-points, Nk, needed for convergence. We set a probable error bar at approximately 20%.
is the p-component of the Berry curvature for the wave-vector k and the components ℓ, m, p are to be chosen cyclic [2]. A limit to our numerical procedure is the rather high number of k-points, Nk, needed for convergence. We set a probable error bar at approximately 20%.
An important relation is useful for understanding of our results. Haldane [18] states that for a non-degenerate, entirely occupied band n the following relation holds:

where the integral is over the Brillouin zone (BZ), 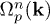 is the p-component of the Berry curvature of band n, Cn is the Chern number of band n and
is the p-component of the Berry curvature of band n, Cn is the Chern number of band n and  is the p-component of a reciprocal lattice vector. The latter quantizes the result. It is the possible non-zero Chern number that leads to striking topological effects.
is the p-component of a reciprocal lattice vector. The latter quantizes the result. It is the possible non-zero Chern number that leads to striking topological effects.
Results and discussion
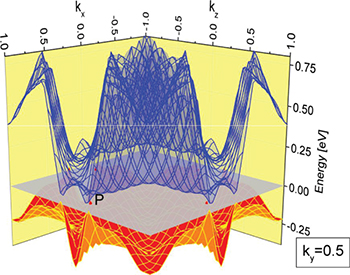
We begin with the energy band structure in its standard form, which is displayed in fig. 1. The bands are spin-filtered, so that the lines in black correspond to spin-minority states, the ones in red to spin-majority bands. The spin orientation was chosen in the (110)-direction. This orientation cannot definitely be established as the ground state since the total energy in the (001)-direction is numerically indistinguishable. A band-crossing is seen to occur slightly above the Fermi energy (energy origin) between the points X and W. We are thus led to look for the energy band-structure inside the BZ choosing a plane in the BZ in order to graph the results in two dimensions. This would naturally be the (xy)-plane, which we chose to name by the normal "z-plane". In fact Wang et al. [14] employ symmetry arguments to demonstrate that in magnetic Heusler compounds Weyl points are expected to exist in the (z = 0)-plane in momentum space. But rather than doing a search directly in this plane, we find it advantageous to start the search in the (x = ± 0.5)- and the (y = ± 0.5)-planes. As an example, we therefore graph the energy-band structure as it is seen from the (y = 0.5)-plane in fig. 2. There are four small Fermi circles (in red) to be seen at the Fermi energy (in grey), one near the point marked P. The star of the corresponding k-vector in the (y = 0.5)-plane under the the 2-fold symmetry operation, rotation about the z-axis times time reversal, 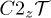 , consist of this point and another one partly covered by the states of band 29 (blue). The remaining two Fermi circles are not in the (z = 0)-plane. In fig. 3 we plot the Berry-curvature computed for the (y = 0.5)-plane. This gives us information about the nearly filled band (and all lower ones because of the sum in the definition of the Berry connection
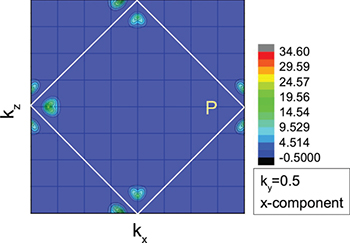
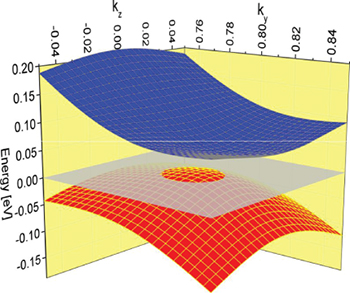
, consist of this point and another one partly covered by the states of band 29 (blue). The remaining two Fermi circles are not in the (z = 0)-plane. In fig. 3 we plot the Berry-curvature computed for the (y = 0.5)-plane. This gives us information about the nearly filled band (and all lower ones because of the sum in the definition of the Berry connection  ). Zooming in on the signal on the left, which originates from the partly covered star of k in fig. 2, we see that its states are gapped as shown in fig. 4. The states are of the same symmetry and the gap disappears if spin orbit coupling (SOC) is removed. Doing the same for the states on the right near the letter P in the figure we find that its states cross. Its energy surfaces are depicted in fig. 5. This is clearly a Weyl point, albeit slightly above the Fermi energy. There are all together four such Weyl points, their coordinates being (0.5, 0.81, 0), (−0.5, −0.81, 0), (0.81, 0.5, 0), and (−0.81,−0.5, 0). They are protected by different eigenvalues of the symmetry operation C2110 [14]. They are easily found by a search in the other planes, each plane hosting one Weyl point. As expected by the above mentioned symmetry arguments, the kz-coordinate is always 0, and each pair is related by inversion symmetry.
). Zooming in on the signal on the left, which originates from the partly covered star of k in fig. 2, we see that its states are gapped as shown in fig. 4. The states are of the same symmetry and the gap disappears if spin orbit coupling (SOC) is removed. Doing the same for the states on the right near the letter P in the figure we find that its states cross. Its energy surfaces are depicted in fig. 5. This is clearly a Weyl point, albeit slightly above the Fermi energy. There are all together four such Weyl points, their coordinates being (0.5, 0.81, 0), (−0.5, −0.81, 0), (0.81, 0.5, 0), and (−0.81,−0.5, 0). They are protected by different eigenvalues of the symmetry operation C2110 [14]. They are easily found by a search in the other planes, each plane hosting one Weyl point. As expected by the above mentioned symmetry arguments, the kz-coordinate is always 0, and each pair is related by inversion symmetry.
Fig. 1: (Color online) Top: the band structure of Co2MnAl along the usual symmetry lines. The magnetization is assumed to be along the (110)-direction. Black lines: minority states, red lines: majority states. Bottom: the Brillouin zone of the fcc lattice.
Download figure:
Standard imageFig. 2: (Color online) Energy surfaces as seen from the (ky = 0.5)-plane. Red: from states number 28; blue: from states number 29; grey: Fermi energy.
Download figure:
Standard imageFig. 3: (Color online) The x-component of the Berry curvature in the (ky = 0.5)-plane, the letter P (corresponding to P in fig. 2) marks the position of a Weyl point, which is found on the right side of P. The white lines enclose the relevant part of the BZ.
Download figure:
Standard imageFig. 4: (Color online) Energy surfaces near a Fermi circle which is cut out by the states drawn in red (from states No. 28), grey: Fermi energy. Color codes correspond to fig. 2.
Download figure:
Standard imageFig. 5: (Color online) Energy surfaces of a Weyl point that is located 30.9 meV above the Fermi energy.
Download figure:
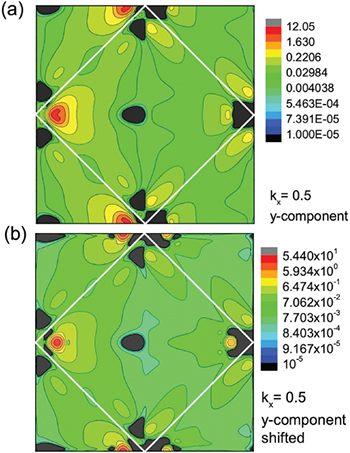
Standard imageIt is to be noted that in contrast to the gapped states, the Weyl point in the lower panel of fig. 3 on the scale plotted leaves no mark to the right of the letter P. A numerical experiment reveals more about this point. We look at the signals of the gapped states and the Weyl point in the self-consistent settings on a logarithmic scale and watch them change when the Fermi energy is increased by 30.9 meV, which brings the Weyl point down to the Fermi edge. This is shown in fig. 6(a) and (b). The Weyl-point in panel (b) becomes distinct fanning out toward the center, while the signal from the gapped states becomes slightly weaker.
Fig. 6: (Color online) Berry curvature in the (kx = 0.5)-plane in a logarithmic presentation. (a) The Fermi energy is located at the self-consistent position. (b) The Fermi energy is shifted such that the Weyl point is at the Fermi energy. The Weyl point in both cases is at the right.
Download figure:
Standard imageKnowing the energy shift that is necessary to bring the Weyl points to the Fermi energy we can now perform a calculation of the Berry curvature to exhibit all Weyl points in the kz = 0-plane. The result is shown in fig. 7 for the −y-component. The four Weyl points are marked as PW. The calculation for the x-component looks similar, except for an interchange of the positive and negative values of the PW's (the reason is the negative y-direction).
Fig. 7: (Color online) The Weyl points, PW, in the (kz = 0)-plane. The Berry curvature shown is in the −y-direction. The standard symmetry points are marked.
Download figure:
Standard imageIt is of interest to notice that the two pairs of Weyl points have different signs. Using the wording of Haldane [18] we can say that these points show properties of "wormholes": Berry flux passes from one band to the other in one pair and returns in the other one, the "space" being momentum space and the "universes" being Bloch bands. Dropping the bloomy language we state that the origin of the sign change are the different chiralities of the two pairs of Weyl points [19]. The other yellow markings in fig. 7 are due to flux through gapped states.
It is to be noted that the number of Weyl points in our calculation is twice as large as that found by Wang et al. [14]. This is interesting since the symmetry arguments used in their paper are applicable one to one to our case, in spite of the fact that Co2MnAl possesses three magnetic ions, a larger number of valence electrons and consequently a different band-structure, compared with the type of Heuslers investigated by Wang et al. The different eigenvalues of the two-fold rotation that makes the band crossing possible depend on symmetry and on the location of the band crossings in the BZ.
A brief excursion to the Heusler compound Co2MnAl assuming a magnetization in the (100)-direction seems in order. The number of symmetry elements is doubled now. Still, going through the described analysis again we find 2 pairs of Weyl points at the same positions as in the (110) case. The energy shift needed to bring these points to the Fermi energy is 30.7 meV, nearly the same as before. Because of the higher number of symmetry elements there might be more Weyl points, however, which a further study will reveal.
Since the electronic structure of Co2MnGa is very similar to that of Co2MnAl having the same number of valence electrons and an extremely similar band structures, we expect to find four Weyl points also in Co2MnGa.
Summary
In the Heusler compound Co2MnAl a large anomalous Hall effect, theoretically and experimentally, finds a possible explanation by a topological argument; the non-zero Chern numbers of the non-degenerate bands near the Fermi energy give rise to the existence of Weyl points, unremovable band crossing near the Fermi energy. There are two pairs in our analysis. However, further calculations of surface states are necessary to substantiate the effect. For technical reasons these have not yet been carried out. The Weyl points are slightly above the Fermi edge, some 30 meV, and should therefore be experimentally observable when the crystal is mildly doped. Theoretically the AHC is large already in the self-consistent calculations through the non-zero Chern numbers; it further increases markedly when the Fermi energy is raised to coincide with the Weyl points.
Acknowledgments
One of the authors (JK) gratefully acknowledges the financial support by the Max-Planck Gesellschaft.