Abstract
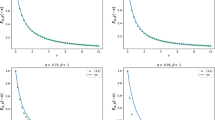
This paper proposes a global Padé approximation of the generalized Mittag-Leffler function Eα,β(-x) with x ∈ [0, ∞). This uniform approximation can account for both the Taylor series for small arguments and asymptotic series for large arguments. Based on the complete monotonicity of the function Eα,β(-x), we work out the global Padé approximation [1/2] for the particular cases (0 < α < 1, β > α), (0 < α = β < 1}, and (a = 1, ß > 1), respectively. Moreover, these approximations are inverted to yield a global Padé approximation of the inverse generalized Mittag- Leffler function -Lα,β(x) with x ∈ (0, 1/Г(β)]. We also provide several examples with selected values a and ß to compute the relative error from the approximations. Finally, we point out the possible applications using our established approximations in the ordinary and partial time-fractional differential equations in the sense of Riemann-Liouville.
Similar content being viewed by others
References
C. Atkinson, A. Osseiran, Rational solutions for the time-fractional diffusion equation. SIAM J. Appl. Math. 71, (2011), 92–106.
M. Concezzi, R. Spigler, Some analytical and numerical properties of the Mittag-Leffler functions. Fract. Calc. Appl. Anal. 418, No 1 (2015), 64–94; DOI: 10.1515/fca-2015-0006; http://www.degruyter.com/view/j/fca.2015.18.issue-1/issue-files/fca.2015.18.issue-1.xml.
K. Diethelm, N.J. Ford, A.D. Freed, Yu. Luchko, Algorithms for the fractional calculus: a selection of numerical methods. Comput. Method. Appl. M. 194, No 6 (2005), 743–773.
M.M. Dzherbashyan, Integral Transforms and Representation of Functions in Complex Domain (in Russian). Nauka, Moscow (1966).
A. Erdélyi, Magnus, F. Oberhettinger, F.G. Tricomi (Eds.), Higher Transcendental Functions. McGraw-Hill, New York (1955).
W. Feller, An Introduction to Probability Theory and Its Applications. 2nd Edition, John Wiley & Sons (1971).
R. Garrappa, Numerical evaluation of two and three parameter Mittag-Leffler function. SIAM J. Numer. Anal. 53, (2015), 1350-169.
R. Garrappa, The Mittag-Leffler function, Matlab Central File Exchange; http://www.mathworks.com/matlabcentral/fileexchange/48154 (8-10-2015).
R. Gorenflo, J. Loutchko, Y. Luchko, Computation of the Mittag-Leffler function Ea,ß(z) and its derivatives. Fract. Calc. Appl. Anal. 5, No 4 (2002), 491–518.
H.J. Haubold, A.M. Mathaiand, R.K. Saxena, Mittag-Leffler functions and their applications. J. Appl. Math. 2011 (2011), Article ID 298628.
R. Hilfer, H.J. Seybold, Computation of the generalized Mittag-Leffler function and its inverse in the complex plane. Integr. Transf. Spec. Funct. 17, No 9 (2006), 637–652.
A.A. Kilbas, M. Saigo, On Mittag-Leffler type function, fractional calculas operators and solutions of integral equations. Integr. Transf. Spec. Funct. 4, No 4 (1996), 355–370.
A.A. Kilbas, M. Saigo, R. Saxena, Generalized Mittag-Leffler function and generalized fractional calculus operators. Integr. Transf. Spec. Funct. 15, No 1 (2004), 31–49.
A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. Elsevier Science Limited (2006).
F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Imperial College Press, London (2010).
F. Mainardi, On some properties of the Mittag-Leffler function Eα(-tα), completely monotone for t > 0 with 0 < α < 1. Discrete Cont. Dyn-B 19, No 7 (2014), 2267–2278.
F. Mainardi, R. Gorenflo, On Mittag-Leffler-type functions in fractional evolution processes. J. Comput. Appl. Math. 118, No 1 (2000), 283–299.
F. Mainardi, R. Gorenflo, Time-fractional derivatives in relaxation processes: A tutorial survey. Fract. Cal. Appl. Anal. 410, No 3 (2007), 269–308; at http://www.math.bas.bg/~fcaa.
K.S. Miller, S.G. Samko, A note on the complete monotonicity of the generalized Mittag-Leffler function. Real Anal. Exchange 23, No 2 (1997), 753–755.
G.M. Mittag-Leffler, Sur la nouvelle fonction Ega(x). C. R. Acad. Sci. Paris 137, (1903), 554–558.
K.B. Oldham, J. Spanier, The Fractional Calculus. Academic Press, New York - London (1974).
J. Peng, K. Li, A note on property of the Mittag-Leffler function. J.Math. Anal. Appl. 370, No 2 (2010), 635–796.
I. Podlubny, Fractional Differential Equations, Academic Press, San Diego (1999).
I. Podlubny, Mittag-Leffler function, Matlab Central File Exchange; http://www.mathworks.com/matlabcentral/fileexchange/8738.
H. Pollard, The completely monotonic character of the Mittag-Leffler function Eα(-x). Bull. Amer. Math. Soc. 54 (1948), 1115–1116.
W.R. Schneider, Completely monotone generalized Mittag-Leffer functions. Expo. Math. 14 (1996), 3–16.
H. Seybold, R. Hilfer, Numerical algorithm for calculating the generalized Mittag-Leffler function. SIAM J. Numer. Anal. 47 (2008), 69–88.
H. Sheng, Y.Q. Chen, T. Qiu, Fractional Processes and Fractional- Order Signal Processing. Springer, London (2012).
S.T. Spencer, J.W. Hanneken, T.R. Ensley, B.N. Narahari, Properties of the Mittag-Leffler function. In: Amer. Phys. Soc. Mar. Meeting, Denver, CO, (2007), Abstract R1.00249.
A.P. Starovoitov, N.A. Starovoitova, Padé approximants of the Mittag- Leffler functions. Sb. Math. 198, No 7 (2007), 1011–1023.
A. Wiman, Über den fundamentalsatz in der teorie der funktionen Eα(x). Acta Math. 29 (1905), 191–201.
S. Winitzki, Uniform approximations for transcendental functions. ICCSA 2003, Springer (2003), 780–789.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Zeng, C., Chen, Y.Q. Global Padé Approximations of the Generalized Mittag-Leffler Function and its Inverse. FCAA 18, 1492–1506 (2015). https://doi.org/10.1515/fca-2015-0086
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1515/fca-2015-0086