Nonlinear indentation of fibers

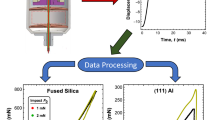
Abstract

An instrumented indentation method is established to accurately measure the local elastic-plastic material properties of a single fiber by accounting for the additional sources of compliance associated with fiber indentation. The Oliver-Pharr instrumented indentation data analysis method is compared for indentation of a standard, planar fused silica sample and in the radial direction of homogeneous, isotropic E-glass fibers of two different diameters. Compliance contributions from substrate deflection and other nonindentation-related fiber deflections are quantified and shown to be negligible. The added compliance observed is attributed to the lack of constraint due to the finite geometry of a curved fiber surface. This compliance contribution is accounted for by using a proposed area correction to capture the geometry of the curved fiber-probe contact combined with a structural compliance correction. Implementation of these corrections to experimental indentation curves results in accurate measurements of the fiber elastic modulus and hardness.

Appendices

Appendix A—Projected Area Corrections for Radial Indentation of a Filament by Various Probes

A. Conical indentation probe

Define the fiber cross-section in Fig. A1 by a circle of radius R centered at (0,0):

$${x^2} + {y^2} = {R^2},$$

((A1))

$$a_{\rm{c}}^2 + {d^2} = {R^2},$$

((A2))

FIG. A1.

Conical probe geometric projected area correction schematic.

Both a_c and d can be defined in terms of the indent depth and indenter and fiber geometry:

$$a_\text{c} = h'_\text{c} \tan \theta,$$

((A3))

$$d = R - {h_{\rm{c}}} + {h'_{\rm{c}}}.$$

((A4))

Substituting (A3) and (A4) back into (A2), expanding, and combining like terms gives h′_c in quadratic form:

$$h'_\text{c} \left(\tan^2 \theta + 1 \right) + h'_\text{c} \left(2R - 2h_\text{c} \right) + \left(h_\text{c}^2 - 2Rh_\text{c} \right) = 0.$$

((A5))

Using the quadratic formula, a solution for$h'_{\rm{c}}$ is found:

$$h'_\text{c} = {h_\text{c} - R + \left(R^2 + 2Rh_\text{c} \tan^2 \theta - h_\text{c}^2 \tan^2 \theta \right)^{1/2} \over \tan^2 \theta + 1}.$$

((A6))

Recognizing (tan²θ + 1) = sec²θ = 1/cos²θ, and dividing through by h_c gives the$h'_{\rm{c}} /h_{\rm{c}}$ solution for a cone:

$${h'_\text{c} \over h_\text{c}} = \cos^2 \theta \left(1 - {R \over h_c} + \left[ \left( {R \over h_c} \right)^2 + 2 {R \over h_c} \tan^2 \theta - \tan^2 \theta \right]^{1/2} \right).$$

((A7))

The elliptical area correction can be found in two manners: 1) considering an ideally shaped probe, and 2) staying consistent with the experiment, and using the calibrated probe area function. The first method depends heavily on the general probe shape used. For a cone, consider the area of an ellipse to be A_ellipse = πab. The major elliptical radius, a, is along the fiber axial direction and is given by, a_f; and the minor elliptical radius, b, falls along the curved transverse profile and given by a_c. Therefore:

$$A_\text{ellipse} = \pi a_\text{c} a_\text{f},$$

((A8))

$$a_\text{f} = h_\text{c} \tan \theta,$$

((A9))

$$a_\text{c} = h'_\text{c} \tan \theta,$$

((A10))

$$A_\text{ellipse} = \pi h_c h'_\text{c} \tan^2 \theta.$$

((A11))

Comparing this to the area function for a circular projection on a flat surface,$A_\text{flat} = \pi a_\text{f}^2,$ gives:

$${\left( {{{{A_{{\rm{ellipse}}}}} \over {{A_{{\rm{flat}}}}}}} \right)_{{\rm<Emphasis Type="ItalicDoubleUnderline">eal</Emphasis>}\,{\rm{Cone}}}} = {{{{h'}_{\rm{c}}}} \over {{h_{\rm{c}}}}}.$$

((A12))

The second method gives a solution that is interchangeable for all probe shapes as long as the probe area function, A, is known. This is the method used herein:

$$A_\text{flat} = \pi a_\text{f}^2 = A \, \text{evaluated} \, \, h_\text{c},$$

((A13))

$$A_\text{curved} = \pi a_\text{c}^2 = A \, \text{evaluated} \, \, h'_\text{c}.$$

((A14))

From these relationships it follows that:

$$a_\text{f} = \left( { A \, \text{evaluated} \, \, h_\text{c} \over \pi } \right)^{1/2},$$

((A15))

$$a_\text{c} = \left( {A \, \text{evaluated} \, \, h'_\text{c} \over \pi} \right)^{1/2}.$$

((A16))

Now using (A8) for A_ellipse, the general area correction ratio is:

$${\left( {{{{A_{{\rm{ellipse}}}}} \over {{A_{{\rm{flat}}}}}}} \right)_{{\rm{General}}}} = {\left[ {{{A\,{\rm{evaluated}}\,{\rm<ArticleTitle Language="En"></ArticleTitle>}\,{{h'}_{\rm{c}}}} \over {A\,{\rm{evaluated}}\,{\rm<ArticleTitle Language="En"></ArticleTitle>}\,{h_{\rm{c}}}}}} \right]^{1/2}}.$$

((A17))

B. Spherical indentation probe

Define the fiber cross section in Fig. A2 as a circle of radius R centered at (0, 0) and the probe as a circle of radius r centered at (0, R + r–h_c):

$${\rm{Fiber}}\,{\rm{:}}\,{x^2} + {y^2} = {R^2}.$$

((A18))

$${\rm<Prefix>obe</Prefix>}\,{\rm{:}}\,{x^2} + {\left( {y - R - r + {h_{\rm{c}}}} \right)^2} = {r^2}.$$

((A19))

FIG. A2.

Spherical probe geometric projected area correction schematic.

The y of interest is that where the fiber and the probe share the same x, or x²:

$${R^2} - {y^2} = {r^2} - {\left( {y - R - r + {h_{\rm{c}}}} \right)^2}.$$

((A20))

Expanding, simplifying, and solving for y gives:

$$y = {{{R^2} + Rr - R{h_{\rm{c}}} - r{h_{\rm{c}}} + {{h_{\rm{c}}^2} \over 2}} \over {R + r - {h_{\rm{c}}}}}\,{\rm<ArticleTitle Language="En"></ArticleTitle>}\,{x_{{\rm<Prefix>obe</Prefix>}}} = {x_{{\rm{fiber}}}}.$$

((A21))

Using the relationship,$R - h_{\rm{c}} = y - h'_{\rm{c}}$ gives$h'_{\rm{c}} = y - R + h_{\rm{c}},$ and dividing through by h_c gives:

$${{{{h'}_{\rm{c}}}} \over {{h_{\rm{c}}}}} = {{{R^2} + Rr - R{h_{\rm{c}}} - r{h_{\rm{c}}} + {{h_{\rm{c}}^{\rm{2}}} \over 2}} \over {R{h_{\rm{c}}} + r{h_{\rm{c}}} - h_{\rm{c}}^{\rm{2}}}} + 1 - {R \over {{h_{\rm{c}}}}}.$$

((A22))

The area correction for a spherical probe can be done using either the general Eq. (A17) or assuming an ideal spherical probe. For an ideal spherical probe, a_f and a_c are:

$${a_{\rm{f}}} = {\left[ {{h_{\rm{c}}}\left( {2r - {h_{\rm{c}}}} \right)} \right]^{1/2}},$$

((A23))

$${a_{\rm{c}}} = {\left[ {{{h'}_{\rm{c}}}\left( {2r - {{h'}_{\rm{c}}}} \right)} \right]^{1/2}}.$$

((A24))

Then the area correction ratio is given as:

$${\left( {{{{A_{{\rm{ellipse}}}}} \over {{A_{{\rm{flat}}}}}}} \right)_{{\rm<Emphasis Type="ItalicDoubleUnderline">eal</Emphasis>}\,{\rm{Sphere}}}} = {{{a_{\rm{c}}}} \over {{a_{\rm{f}}}}} = {\left[ {{{{{h'}_{\rm{c}}}\left( {2r - {{h'}_{\rm{c}}}} \right)} \over {{h_{\rm{c}}}\left( {2r - {h_{\rm{c}}}} \right)}}} \right]^{1/2}}.$$

((A25))

C. Spheroconical indentation probe

The spheroconical probe contact correction can be best described by a piecewise function separated at the transition point between spherical and conical probe shape. This transition point is at the tangent point between line 1 defined by the conical region of the probe and the spherical end of the probe defined by radius r (Fig. A3). The tangent point, (x₁, y₁) will be where the slopes are equal. The slope of line 1 is given by cot(θ), and the spherical portion of the probe can be defined as x² + y² = r² which gives a slope, dy/dx:

$${{{\rm{d}}y} \over {{\rm{d}}x}} = {x \over {{{\left( {{r^2} - {x^2}} \right)}^{1/2}}}}.$$

((A26))

FIG. A3.

Spheroconical probe geometric projected area correction schematic.

FIG. A4.

SYS plots used to measure the structural compliance, C_s, and Joslin–Oliver parameter, J_o, of the 23-μm (left) and 10-μm (right) E-glass fibers.

The slopes are found to be equal when x₁ = rcosθ and y₁ = rsinθ. This point can be used to find the intersection of lines 1 and 2, which gives y₂. The lines are defined as:

$$y1 = \cot \theta \left( x1 - x_1 \right) - y_1,$$

((A27))

$$y2 = \cot \theta \left(x2 + x_1 \right) - y_1,$$

((A28))

From the schematic, y1 = y2 = y₂ when x = 0. Therefore,

$$y_2 = - r \left(\text{sin} \theta + \text{cos} \theta \cot \theta \right),$$

((A29))

The distance h_d is the indent depth lost due to the rounding of a conical tip, and is given by:

$$h_\text{d} = \left| y_2 \right| - r = r\left( \sin \theta + \cos \theta \cot \theta - 1 \right).$$

((A30))

The relationship between$h'_{\rm{c}}$ and h_c for a spheroconical tip is then given by the spherical relationship (A22) at depths below the sphere-cone transition depth of$r - \left| {y_1 } \right|$, or h_c < r(1 − sinθ). At depths greater than r(1 − sinθ), the conical relationship (A7) can be used by substituting$h'_{\rm{c}} + h_{\rm{d}}$ for$h'_{\rm{c}}$ and h_c+ h_d for h_c, giving:

$${{{{h'}_{\rm{c}}} + {h_{\rm{d}}}} \over {{h_{\rm{c}}} + {h_{\rm{d}}}}} = f,$$

((A31))

((A32))

With simplification, this ultimately gives the piecewise function for$h'_{\rm{c}} /h_{\rm{c}}$ of a spheroconical probe governed by the sphere at low depths and a cone at greater depths:

((A33))

Similarly, the corrected area can be found using Eq. (A17) using the calibrated probe area function; or for an ideal spheroconical probe the area is given by that of a sphere at indent contact depth h_c at low depths and by a cone at an indent contact depth h_c + h_d at greater depths:

((A34))

Appendix B—Sys Plots of The E-Glass Fibers

The correction for structural compliance used when measuring the material properties of the glass fibers is extracted from the SYS plots for the 10- and 23-μm fibers portrayed below. The plots show one representative SYS curve for each indentation depth on each fiber.

The correlation depth indicated in Fig. A4 corresponds to the probe transition from spherical to conical in shape. This transition limits the linear fit region to contact depths greater than approximately 290 nm33 and restricts the SYS parameter measurements on the 10-μm fiber to only the maximum indent depth of 800 nm. Beyond this depth, the SYS compliance plots are linear, indicating that the sources of compliance associated with fiber indentation are independent of indent load, and validating the use of the Jakes et al. compliance method. The values for C_s and J_o, in Table I, are averages for all the applicable indents [i.e., five (5) 800 nm indents on the 10-μm fiber and five at each depth totaling twenty (20) on the 23-μm fiber]. The ranges given in Table I are representative of one standard deviation of the applicable measurements.

TABLE I.

Fiber indentation structural compliance, C_s, and Joslin–Oliver parameter, J_o, for the 10- and 23-μm E-glass fibers.

Based solely on the geometry of the probe-fiber contact, the relative constraining volume decreases with indent depth, which would cause an increase in the structural compliance with indent depth. Conversely, in Fig. A4, the structural compliance (slope of the SYS plot) decreases until it reaches an approximately constant value at greater indent depths (loads). Our preliminary understanding is that stress contour modifications and the material pile-up around the indenter appear to mitigate the curvature such that the structural compliance reaches a plateau value.