Measuring substrate-independent modulus of thin films

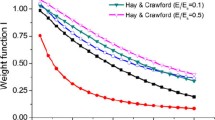
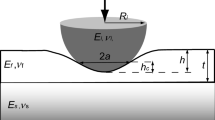
Abstract

Substrate influence is a common problem when using instrumented indentation (also known as nano-indentation) to evaluate the elastic modulus of thin films. Many have proposed models to be able to extract the film modulus (E_f) from the measured substrate-affected modulus, assuming that the film thickness (t) and substrate modulus (E_s) are known. Existing analytic models work well if the film is more compliant than the substrate. However, no analytic model accurately predicts response when the modulus of the film is more than double the modulus of the substrate. In this work, a new analytic model is proposed. This new model is shown by finite-element analysis to be able to accurately predict composite response over the domain 0.1 < E_f/E_s < 10. Finally, the new model is used to analyze experimental data for compliant films on stiff substrates and stiff films on compliant substrates.

Appendix

The model proposed here presumes that an apparent shear modulus, μ_a, has already been determined. This appendix summarizes the process for determining μ_a. Analysis is presented in reverse chronological order so as to emphasize motivation. That is, in practice, stiffness is calculated first and apparent shear modulus [Eq. (A1) ] is calculated last. The apparent shear modulus is calculated from the apparent Young’s modulus as

$${{{\mu }}_{\rm{a}}} = {{{E_{\rm{a}}}} \over {2\left( {1 + {v_{\rm{a}}}} \right)}}\quad.$$

((A1))

The apparent Young’s modulus is calculated from the apparent reduced modulus (E_r–a) as

$${E_{\rm{a}}} = \left( {1 - v_{\rm{a}}^2} \right)\left[ {{1 \over {{E_{{\rm{r}} - {\rm{a}}}}}} - {{1 - v_{\rm{i}}^2} \over {{E_{\rm{i}}}}}} \right]\quad,$$

((A2))

where E_i and ν_i represent the properties of the indenter material—in this case diamond (E_i = 1140 GPa and ν_i = 0.07). The apparent reduced modulus is calculated as

$${E_{{\rm{r}} - {\rm{a}}}} = {{\sqrt {{\pi }} } \over 2}{S \over {\sqrt A }}\quad,$$

((A3))

where A and S are the projected normal contact area and contact stiffness, respectively.

The methods for determining A and S are different, depending on whether the data are simulated or experimental. Let us first consider contact area, A, and then contact stiffness, S. One way to calculated contact area is as a function of contact depth,

$$A = f\left( {{h_c}} \right)\quad,$$

((A4))

where h_c is calculated by the method of Oliver and Pharr1 from force (P), displacement (h), and contact stiffness (S) as

$${h_c} = h - 0.75P/S\quad.$$

((A5))

This Oliver–Pharr method was applied to both simulated and experimental data, with some subtle distinctions. First, the function for relating contact depth to contact area [Eq. (A4) ] is known precisely in simulation—it is basically an input used to place the boundary nodes for the indenter. For experiments, however, the functional relationship of Eq. (A4) is determined empirically by indenting fused silica—a material of known and isotropic Young’s modulus. Second, the method for determining S for use in Eq. (A5) is different for simulation and experiment as will be explained shortly. In addition to determining contact area by means of the Oliver–Pharr method, simulations permit an alternate determination of contact area from the contact radius, a, as determined from the finite-element mesh. Thus, for simulations only, contact area was also calculated as

$$A = {{\pi }}{a^2}\quad.$$

((A6))

Thus, in Fig. 4, we compare contact area as determined by Eq. (A4) with that determined by Eq. (A6), presuming that Eq. (A6) gives the “true value.” For the simulated results plotted in Figs. 5–7, it is Eq. (A6) that is used to determine A for use in Eq. (A3). For the experimental results plotted in Figs. 8–13, it is Eq. (A4) that is used to determine A for use in Eq. (A3).

The contact stiffness (S), which is used in Eqs. (A3) and (A5 ), is also determined differently for simulation and experiment, but this is because our experiments are not simple load–unload tests, but involve applying a small oscillation to the indenter. That is, if our experiments were semi-static, we would determine S in the same way for both experiment and simulation. For simulated data, S is the slope of the force–displacement curve when the indenter is first withdrawn from the test material. For experimental data, S is basically the amplitude of the force oscillation divided by the amplitude of the displacement oscillation. An explanation of the processes for determining S by these two means is beyond the scope of this appendix. The reader is invited to consult reference15 for an explanation of the semi-static method and reference16 for an explanation of the oscillating method. However, one practical difference is worth noting here. The semi-static method yields only one measure of stiffness; thus, each simulated test yields only one value for E_r–a, E_a, μ_a, and μ_f. This is why many simulations had to be performed, each to a different depth, to examine the relevant domain of h/t. By contrast, each experimental test yields S as a continuous function of penetration depth because of the small oscillation imposed on the indenter. Thus, the experimental tests yield continuous measures of E_r–a, E_a, μ_a, and μ_f as a function of indentation depth. Multiple experimental tests on a single sample are consolidated by averaging into discrete displacement windows.

Nomenclature

a

contact radius

A

contact area

P

applied force

h

displacement of the indenter into the test surface

h_c

contact depth

t

effective film thickness (original film thickness less contact depth)

I₀

weighting factor for modulus (of Gao et al.)

I₁

weighting factor for Poisson’s ratio (of Gao et al.)

F

empirical constant (dimensionless)

D

this constant has the value of 4a/(1–ν_a). Generally, contact stiffness is given by the expression Dμ.

E

Young’s modulus

ν

Poisson’s ratio

μ

shear modulus

S

contact stiffness

κ

dielectric constant

a

as a subscript: apparent (substrate-affected)

i

as a subscript: of the indenter

f

as a subscript: of the film

r

as a subscript: reduced

s

as a subscript: of the substrate