Functional properties of rough surfaces from an analytical theory of mechanical contact

Abstract

The basic ideas behind a contact mechanics theory for randomly rough surfaces are presented. The theory is based on studying the interface at increasing magnification. At the lowest magnification, no surface roughness can be detected and the nature of the contact between two solids in this limit can be determined using standard numerical methods (e.g., FEM). The theory predicts how the surface roughness influences (or modifies) the contact stress distribution and the interfacial gap. The theory is flexible and can be applied to elastic, viscoelastic, and elastoplastic solids, as well as layered materials. Applications to leakage of seals, contact stiffness, the electric and thermal contact resistance, rubber friction, adhesion, and mixed lubrication are presented.

Graphical abstract

Introduction

In the design of engineering structures, surfaces of solids are usually assumed to be smooth. This assumption is a valid approximation (e.g., when choosing the dimension of steel beams for a bridge). However, many phenomena such as adhesion, friction, and wear depend in a crucial way on surface roughness.^1,2,3,4

Surface roughness usually extends over many decades in length scales. An asphalt road surface, for example, may be designed to be nominally flat, but is rough starting at length scales determined by the biggest stone particles in the asphalt and extending down to atomic distances (i.e., from ~1 cm to ~1 nm or 7 decades in length scale). Obtaining the microscopic stress acting between a tire and a road surface may require solving a problem with $10^{7}\times 10^{7} =10^{14}$ surface grid points, which is impossible to do directly, even on a supercomputer. For this reason, it is important to develop analytical methods to handle problems involving multiscale roughness. In this article, we will describe one such method that has been applied to a large number of practical problems such as adhesion, rubber friction, and sealing. We will not present any derivations, but rather focus on the basic idea underlying this approach.

Figure 1

A surface that appears smooth to the naked eye (e.g., a surface of a table) will exhibit roughness when observed at some magnification $\upzeta$. And an asperity that appears smooth at the magnification $\upzeta$ will exhibit surface roughness when observed at higher magnification.

Figure 2

A general surface profile $z=h(x)$ can be decomposed into a sum of cosines and sine waves of different wavelength $\uplambda$ (or wave number $q=2\uppi /\uplambda$) and different amplitudes $h_{\text{q}}$. The surface roughness power spectrum $\sim |h_{\text{q}}|^{2}.$

Surface roughness

All surfaces of solids have surface roughness on many different length scales. When a surface is observed with the naked eye, it may appear smooth, but when observed with an optical microscope, we detect surface roughness. A bump (asperity) on the surface, which appears smooth at a particular magnification $\upzeta$ will exhibit roughness when studied at higher magnification (e.g., using an electron microscope [see Figure 1]). Because contact mechanics depends on the roughness on all length scales, we need some quantity that describes the roughness on all length scales. The most useful such quantity is the surface roughness power spectrum $C({\mathbf{q}}).$^5,6,7,8 For a randomly rough surface, all of the (ensemble-averaged) information about the surface roughness is contained in $C({\mathbf{q}})$. The power spectrum is defined as the square of the surface roughness amplitude in wavevector space (see Figure 2). From $C({\mathbf{q}})$ standard quantities such as the root-mean-square (rms) roughness amplitude $h_{{{{\text {rms}}}}}$ or the rms slope $\upxi$ of the surface can be easily calculated.

Surface roughness can be studied over all relevant length scales by combining different experimental methods. Thus, using atomic force microscopy and engineering stylus measurements, all length scales from nanometer to centimeter or more can be studied. Other methods that have been used are optical and transmission electron microscopy. For surfaces with roughness with isotropic statistical properties, it is enough to measure the topography over a (long enough) line to get the one-dimensional (1D) height profile $z=h(x)$. For anisotropic roughness it is necessary to measure over an area to get the 2D height profile $z=h(x,y)$. For isotropic surface roughness $C({\mathbf{q}})$ is only a function of the wave number $|{\mathbf{q}}| = 2 \uppi /\uplambda$, where $\uplambda$ is the wavelength of a roughness component.

For the contact between two elastic solids 1 and 2 with uncorrelated roughness, the power spectrum of the combined roughness is just the sum of the individual power spectra: $C({\mathbf{q}})=C_{1}({\mathbf{q}})+C_{2}({\mathbf{q}})$.

Figure 3

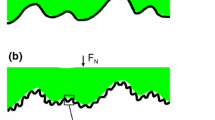
The contact between a rigid solid with a smooth surface and an elastic solid with a rough surface. At low magnification $\upzeta =1$, no roughness can be observed and it appears as if the contact is complete. At higher magnification roughness is observed and now it is observed that contact only occurs at high asperities.

Contact between solids with random roughness

Any two solid objects, even if produced in the same way, will have different surface roughness h(x, y). Hence, the contact stress field $\upsigma (x,y)$ and the gap height (surface separation) field u(x, y) will depend on microscopic details, which in general are unknown, and which vary rapidly and irregularly on a huge number of length scales down to atomic distances. For this reason, only ensemble-averaged quantities are useful and well-defined quantities. In particular, we are interested in the probability distribution of contact stress and gap height.

We will discuss a theory that predicts accurately the contact area, the contact stress distribution, and the distribution of interfacial separations.^{9,10,11,12,13,14} The theory is based on studying how contact stress probability distribution $P(\upsigma ,\upzeta )$ changes with the magnification $\upzeta$ (see Figure 3).

Consider squeezing together two elastic solids with nominally flat surfaces with a uniform applied stress $\upsigma _{0}$. If we assume that there is no friction at the interface, then at the lowest (say naked eye) magnification $\upzeta = 1$ we do not observe any roughness and it appears as if the stress at the interface equals the applied stress $\upsigma _{0}$. In this case, the probability distribution of stresses at the interface will consist of a high and narrow peak with area 1 and centered at the applied stress $\upsigma _{0}$. This function is denoted as the Dirac delta function $P(\upsigma ,1) =\delta (\upsigma -\upsigma _{0})$. Next, we increase the magnification and observe surface roughness as indicated in Figure 3. In this case, the stress probability distribution $P(\upsigma ,\upzeta )$ will broaden with tails extending to both larger and smaller stress than the applied stress $\upsigma _{0}$. One can show that this broadening process is similar to a diffusion process where time is replaced by magnification $\upzeta$ and spatial coordinate with the stress $\upsigma$, and that $P(\upsigma ,\upzeta )$ obey approximately the diffusion equation:⁹

$${\partial P \over \partial \upzeta } = D(\upzeta ) {\partial ^{2} P \over \partial \upsigma ^{2}} .$$

(1)

The diffusivity D is determined by the elastic properties of the solids and by the surface roughness power spectrum:

$$D(\upzeta ) = {\uppi \over 4} \left( {E\over 1-\upnu ^{2}}\right) ^{2} q_{0} q^{2} C(q),$$

where $q=q_{0} \upzeta$, where $q_{0}$ is the wave number of the longest wavelength roughness component (which is equal to $\uppi /L$ or larger, where L is the linear size of the system). Here, we have assumed an elastic solid with the effective modulus $E^{*}=E/(1-\upnu ^{2})$ (E is the Young’s modulus and $\upnu$ the Poisson ratio) in contact with a rigid solid, but the theory is also valid for two elastic solids 1 and 2 in which case $1/E^{*} = (1-\upnu _{1}^{2})/E_{1}+(1-\upnu _{2}^{2})/E_{2}.$

Solving (1) requires boundary conditions and for elastic contact without adhesion one can show that:

$$P(0,\upzeta ) = 0, \quad P(\infty , \upzeta ) = 0, \quad P(\upsigma , 1) = \delta (\upsigma -\upsigma _{0}).$$

The first equation is related to the fact that without adhesion there can be no negative (tensile) stress at the interface and the second condition state that there can be no infinite high stress. The third condition is valid only if the applied stress results in a uniform nominal stress at the interface, and needs to be modified if the nominal stress is different (e.g., parabolic as in a Hertz contact). Solving these equations gives the interfacial stress distribution and the relative area of contact

$${A\over A_{0}} = {{{\text {erf}}}} \left( {\surd 2 \upsigma _{0} \over \upxi E^{*}}\right) ,$$

where ${{{\text {erf}}}}$ is the error-function, and where $\upxi$ is the rms slope of the surface, which can be calculated from the power spectrum using

$$\upxi ^{2} = 2\uppi \int _{q_{0}}^{\upzeta q_{0}} {\text {d}}q \ q^{3} C(q).$$

Note that the rms slope $\upxi$ depends on the magnification $\upzeta$; when we increase the magnification, we observe more short wavelength roughness, the rms slope increases, and the relative contact area $A/A_{0}$ decreases. Thus, the apparent contact observed with an optical microscope would in general be bigger than what is observed with an electron microscope with higher magnification. The true (or real) contact area is obtained by including all the roughness down to atomic distances (say a few Angstrom), corresponding to the highest magnification $\upzeta _{1} = q_{1}/q_{0}$.

Figure 4

The relative contact area $A/A_{0}$ as a function of the applied pressure, p. The numerical exact result is from References 15, 16.

Contact mechanics problems involving two or at most three decades in length scales can be solved numerically exactly, and have been used to test the theory previously presented.¹⁴ As an example, in Figure 4, we show how the area of contact depends on the applied pressure $p=\upsigma _{0}$.

The average interfacial separation and the distribution of interfacial separation

In many applications, the (relative) area of real contact is very small and the surfaces are separated by an air or fluid film in most places. The gap field between two solids is important for fluid flow at the interface (e.g., for the leakage of seals). In some applications, the average gap height (average surface separation) is enough, but in most applications, the probability distribution of gap heights is needed. When the applied stress $\upsigma _{0}$ is such that the relative contact area is much less than 1 (but not so small that finite-size effects become important), the average separation ${{\bar{u}}}$ is related to the squeezing pressure $\upsigma _{0}$ as¹⁰

$$\upsigma _{0} = \upbeta E^{*} {\text {e}}^{-{{\bar{u}}}/u_{0}},$$

(2)

where $u_{0} \approx h_{{{{\text {rms}}}}}$ and $\upbeta$ both are determined by the surface roughness power spectrum $C({\mathbf{q}})$. The theory also predicts the probability distribution of separations.^12,13

Generalizations

A beautiful aspect of the contact mechanics approach previously presented is that the theory can easily be extended to more complex situations. Thus, both solids can have surface roughness and elasticity, and the theory can be applied to viscoelastic⁹ and elastoplastic^9,17 solids, and to layered materials.¹⁸ In addition, it is possible to include adhesion.^19,20

As an example, plasticity can be included in an approximate way by replacing the boundary condition $P(\infty , \upzeta )=0$ with $P(\upsigma _{{{{\text {P}}}}},\upzeta ) =0$, where $\upsigma _{{{{\text {P}}}}}$ is the penetration hardness obtained using, for example, a Vickers or Brinell hardness test.

When adhesion is important, negative (tensile) stresses will occur at the interface. In this case, the boundary condition $P(0, \upzeta )=0$ is replaced by $P(-\upsigma _{{{{\text {a}}}}} (\upzeta ),\upzeta ) =0$, where $\upsigma _{{{{\text {a}}}}}(\upzeta )$ is the highest tensile stress, which occurs at the interface when it is observed at the magnification $\upzeta$. This dependency on the tensile stress on the magnification is similar to the influence of surface roughness on the fluid contact angle on surfaces with roughness: the macroscopic contact angle, as observed by, for example, the naked eye, is in general different from the microscopic contact angle, as would be observed on a perfectly flat surface of the same material.

Layering of the elastic properties can be included in the theory by replacing the effective elastic modulus $E^{*}$ with $E^{*}/S(q)$, which in some applications is equivalent to replacing the surface roughness power spectrum C(q) with $C(q)|S(q)|^{2}$, where the wave number dependent factor S(q) can be calculated analytically.

The theory presented here has been compared against computationally intensive numerical models that compute the exact value for contact properties.^15,16 Figure 4 shows that the (numerically exact) contact area as a function of the squeezing pressure tends to be about $\sim 20\%$ larger at small pressures (where A varies linearly with p) than predicted by the theory. When the squeezing pressure increases, the deviation becomes smaller and vanishes at complete contact. Similarly, analysis of the (average) interfacial separation as a function of the applied pressure indicates that the elastic energy in the asperity contact regions may be slightly overestimated in the theory at low squeezing pressure, while the difference decreases at higher squeezing pressures and vanishes for complete contact. These two facts are related and can be corrected for, and result in a contact area and interfacial separation in close agreement with the numerically exact results.^21,22

Applications

Leakage of seals

Consider first a seal where the nominal contact area is a square. The seal separates a high pressure fluid on one side from a low pressure fluid on the other side, with the pressure drop $\Updelta P$. We consider the interface between the solids at increasing magnification $\upzeta$. At low magnification, we observe no surface roughness and it appears as if the contact is complete. Therefore, studying the interface only at this magnification, we would be tempted to conclude that the leak-rate vanish. However, as we increase the magnification $\upzeta$, we observe surface roughness and noncontact regions (see Figure 5), so that the contact area $A(\upzeta )$ is smaller than the nominal contact area $A_{0} = A(1)$. As we increase the magnification further, we observe shorter wavelength roughness, and $A(\upzeta )$ decreases further. For randomly rough surfaces, as a function of increasing magnification, when $A(\upzeta )/A_{0} \approx 0.42$ the noncontact area percolates,²⁴ and the first open channel is observed, which allows fluid to flow from the high pressure side to the low pressure side. The percolating channel has a most narrow constriction over which most of the pressure drop $\Updelta P$ occurs. In the simplest picture, one assumes that the whole pressure drop $\Updelta P$ occurs over this critical constriction, and if it is approximated by a rectangular pore of height $u_{{{{\text {c}}}}}$, much smaller than its width (as predicted by contact mechanics theory), the leak-rate can be approximated by:²³

$$\dot{Q} = {u_{{{{\text {c}}}}}^{3} \over 12 \upeta }\Updelta P,$$

(3)

where $\upeta$ is the fluid viscosity. The height $u_{{{{\text {c}}}}}$ of the critical constriction can be obtained using the contact mechanics theory previously described. The result (3) is for a seal with a square nominal contact area. For a rectangular contact area with the length $L_{x}$ in the fluid flow direction and $L_{y}$ in the orthogonal direction, there will be an additional factor of $L_{y}/L_{x}$ in (3).

Figure 5

The contact region (black) at different magnifications $\upzeta = 3$, 9, 12, and 648, is shown in (a–d)y, respectively. When the magnification increases from 9 to 12, the noncontact region (white area) percolates (i.e., an open [noncontact] channel extending from one side to the opposite side appears for the first time). The figure is the result of molecular dynamics simulations of the contact between elastic solids with randomly rough surfaces. Adapted from Reference 23.

Figure 6

Square symbols: the measured leak-rate for different rubber–counter surface (squeezing) pressures. The red and green solid lines are the calculated leak-rates using the critical junction theory and the Bruggeman effective medium theory, respectively. Results are shown for sandpaper and sandblasted PMMA surfaces.

The critical junction theory has been tested experimentally for several different systems.^{23,25,26,27,28} The square symbols in Figure 6 show the measured water leak-rate, as a function of the (squeezing) pressures, for a rubber square-ring seal squeezed against sandpaper and two sandblasted plexiglass (PMMA) substrates. The red solid lines show the calculated leak-rates using the critical junction theory. The green solid lines are the calculated leak-rates using the Bruggeman effective medium theory, where all of the flow channels are included in an approximate way.^25,26,27,28

Figure 7

(a) Scattering of elastic waves from a buried interface. (b) The average surface separation ${{\bar{u}}}$ depends on the applied pressure, p. (c) Effective spring model with the spring stiffness depending on the applied pressure, p.

Figure 8

The perpendicular contact stiffness as a function of the squeezing pressure (log–log scale). For an elastic solid with $E^{*}=E/(1-\upnu ^{2})=100 \ {{{\text {GPa}}}}$ and with a randomly rough (self-affine fractal) surface with the rms-roughness amplitude $1 \, \upmu {{{\text {m}}}}.$

Contact stiffness

Scattering of elastic waves from interfaces between solids is one of the most important nondestructive ways to study buried interfaces (e.g., to detect flaws or crack-like defects). Because of surface roughness, an interface of solid contact is usually less stiff than the bulk material, and is often represented as a layer of elastic springs (see Figure 7). If two solids with a nominal flat interface are squeezed together with the nominal pressure, p, the normal contact stiffness is defined as $K=-{\text {d}}p/{\text {d}}{{\bar{u}}}$. If the pressure is not too high (as to approach complete contact) or too low (where finite-size effects become important) then for elastic contact (2) holds and

$$K = {1\over u_{0}} \upbeta E^{*} {\text {e}}^{-{{\bar{u}}} / u_{0}} = {p\over u_{0}}.$$

In Figure 8, we show the contact stiffness over a wide pressure range where both finite-size effects and approach of complete contact occur.^7,29

The contact stiffness theory has been tested experimentally for both elastically soft materials such as rubber,^30,32 and for elastically stiff materials.³³ In both cases, a linear dependency of the stiffness on the squeezing pressure was found with $K\approx p/u_{0}$ with $u_{0} \approx h_{{{{\text {rms}}}}}$. For metals, plastic flow is expected at the asperity level, which will effectively increase the stiffness.

Note that $h_{{{{\text {rms}}}}}$ and hence the contact stiffness are determined mainly by the longest wavelength roughness, and in most cases it is not necessary to study the surface topography h(x, y) at high magnification in order to obtain the contact stiffness.

Figure 9

The electric current at the interface is highly nonuniform, but becomes nearly uniform a short distance from the interface where the electric potential is $\upphi _{1}$ in solid 1 and $\upphi _{2}$ in solid 2.

Heat and electric contact resistance

If an electric potential is applied between two metallic solids in contact, an electric current will flow from one solid to the other via the asperity contact regions (see Figure 9). The interfacial resistance to the current flow is denoted as the electric contact resistance. The electric contact conductance per unit area $\alpha _{{{{\text {el}}}}}$ is defined by

$$J_{z} = \alpha _{{{{\text {el}}}}} (\upphi _{1}-\upphi _{2}),$$

where $J_{z}$ is the electric current and $\upphi _{1}$ and $\upphi _{2}$ are the electric potential in the two solids close to the interface, at such distance from the interface that the electric potential is nearly uniform in the plane parallel to the interface. In a similar way, one can define a thermal contact conductance per unit area by $J_{z} = \alpha _{{{{\text {th}}}}} (T_{1}-T_{2})$, where $J_{z}$ is the thermal current, and $T_{1}-T_{2}$ the temperature change over the interface.

It has been shown by Barber³⁴ (see also References 29, 35) that the heat and electric contact resistance are closely related to the mechanical contact stiffness K. The fundamental reason for this is the similarities between the equations determining elastic deformations and the temperature in thermal contact, and the electric potential in electric contacts. For the latter two phenomena conservation of heat and of electric charge gives $\nabla \cdot \mathbf{J} = 0$ where $\mathbf{J} = - \upkappa _{{{{\text {th}}}}} \nabla T$ for the heat current and $\mathbf{J} = - \upkappa _{{{{\text {el}}}}} \nabla \upphi$ for the electric current. This gives $\nabla ^{2} T=0$ and $\nabla ^{2} \upphi =0$, respectively. These equations are similar to the continuum mechanics equation determining elastic deformations in the static limit. In particular, Boussinesq has shown that if an elastic halfspace is loaded by a normal stress, the solution involves a function $\uppsi$, which satisfies $\nabla ^{2} \uppsi =0$. Using this one can show that³⁴

$$\alpha _{{{{\text {el}}}}} = 2 \upkappa _{{{{\text {el}}}}}^{*} {K \over E^{*}},\quad \alpha _{{{{\text {th}}}}} = 2 \upkappa _{{{{\text {th}}}}}^{*} {K \over E^{*}},$$

where $1/\upkappa _{{{{\text {el}}}}}^{*} = 1/\upkappa _{{{{\text {el}}}}}^{(0)} +1/\upkappa _{{{{\text {el}}}}}^{(1)}$, and where $\upkappa _{{{{\text {el}}}}}^{(0)}$ and $\upkappa _{{{{\text {el}}}}}^{(1)}$ are the electric conductivity of solid 1 and 2, respectively. The effective thermal conductivity $\upkappa _{{{{\text {th}}}}}^{*}$ is defined in a similar way.

Because the mechanical contact resistance is mainly determined by the long wavelength roughness, it follows that the same is true for the electric and the thermal contact resistance. Information about the short wavelength roughness is in most cases not needed when determining the electrical and thermal contact resistance.

The results previously presented assume that the contact resistance is entirely due to the current constrictions involving homogeneous materials and no contamination or oxide films. Thin oxide and contamination films may have a negligible influence on the thermal contact resistance, but could affect the electric contact resistance hugely, unless the local contact pressure is big enough to break up these films.³⁶ In addition, the noncontact area could be very important for heat transfer via heat diffusion in the surrounding gas, or via blackbody heat radiation, which can be strongly enhanced at short surface separation because of the near field (evanescent) part of the electromagnetic field.^35,38,39

Figure 10

The measured and calculated friction coefficient as a function of the logarithm of the sliding speed. Measurements were performed on dry contact (red filled squares), in water (stars) and in water + soap (blue open squares). The blue line is the total calculated rubber friction coefficient and the green line the viscoelastic contribution. For rubber block sliding on an asphalt substrate at the temperature $T=15 ^{\circ} {{{\text {C}}}}$. For higher temperatures the $\upmu (v)$ curve shift to higher sliding speeds. Adapted from Reference 37.

Rubber friction

There are several different contributions to rubber friction, the relative importance of which depends on the rubber compound and countersurface properties. For hard substrates, such as road surfaces, a contribution to rubber friction arises from the time-dependent viscoelastic deformations of the rubber by the substrate asperities. That is, during sliding, an asperity contact region with linear size d will deform the rubber at a characteristic frequency $\upomega \approx v/d$, where v is the sliding speed. Because real surfaces have roughness over many decades in length scales, there will be a wide band of perturbing frequencies, all of which contribute to the viscoelastic part $\upmu _{{{{\text {visc}}}}}$ of the rubber friction coefficient. In addition, there will be a contribution $\upmu _{{{{\text {con}}}}}$ to the friction from shearing the area of real contact.

The viscoelastic contribution, and the rubber–road area of real contact, can be calculated using the contact mechanics theory previously described and depend on the surface roughness power spectrum $C({\mathbf{q}})$ and on the rubber viscoelastic modulus $E(\upomega )$ (a complex quantity with the imaginary part related to energy dissipation). Neglecting frictional heating, the friction coefficient for a rubber block squeezed against a randomly rough and rigid substrate with the pressure $p_{0}$ and sliding at the speed v, is given by^9,40

$$\begin{aligned} \upmu _{{{{\text {visc}}}}}\approx & {} {1\over 2} \int _{q_{0}}^{q_{1}}{\text {d}}q \ q^{3} \ C(q) P(q) \\&\quad \times \int _{0}^{2\uppi } {\text {d}}\upphi \ {{{\text {cos}}}}\ \upphi \ {{{\text {Im}}}}{E(qv \ {{{\text {cos}}}} \ \upphi )\over (1-\upnu ^{2})p_{0}}, \end{aligned}$$

where

$$P(q)= {{{\text {erf}}}}\left( { 1\over 2 \surd G}\right) ,$$

where

$$G(q)={1\over 8}\int _{q_{0}}^{q} {\text {d}}q \ q^{3} C(q) \int _{0}^{2\uppi } {\text {d}}\upphi \ \left| {E(qv \ {{{\text {cos}}}} \ \upphi )\over (1-\upnu ^{2}) p_{0}}\right| ^{2}.$$

Here, $q_{0}$ and $q_{1}$ are the wave numbers of the longest and shortest wavelength roughness components included in the calculation. The relative area of rubber–substrate contact is given by $A/A_{0} = P(q_{1})$.

The contribution $\upmu _{{{{\text {con}}}}}$ to the friction from the area of contact is usually written as $\upmu _{{{{\text {con}}}}} = \uptau (v) A(v)/ (p_{0} A_{0})$, where $\uptau (v)$ is the frictional shear stress acting in the area of real contact, which may be due to polymer segments (or patches of rubber) at the rubber–road interface performing cyclic binding–stretching–breaking interactions.⁴¹ However, rubber wear, and the adhesion enhancements of the area of real contact,⁴² may also be involved and there is at present no generally established consensus on the origin of $\upmu _{{{{\text {con}}}}}$, and also on how to choose the cutoff wave number, $q_{1}$. Nevertheless, in most cases, $\upmu (v)$ depends on the sliding speed as shown in Figure 10, with a low velocity peak usually around ~1 cm/s, attributed to the contribution from the area of contact, and the high velocity peak around $1 \ {{{\text {m/s}}}}$ or more, due to the viscoelastic contribution. The theory previously presented predicts that rubber friction is strongly temperature dependent, which is the reason why in F1-racing the tires are heated up before the start of a race.

Figure 11

The work of adhesion (proportional to the pull-off force) as a function of the number of contacts between smooth and rough (sandblasted) glass balls and soft and stiff silicone rubber with flat surfaces. The pull-off velocity $v \approx 1 \, \upmu {{{\text {m/s}}}}.$

Adhesion

Even the weakest force field of interest in adhesion, namely the (always acting) van der Waals interaction, which is due to quantum (and thermal) fluctuations in the charge distribution in solids, is strong on a macroscopic scale. Because of this, it is possible to keep the weight of a car suspended in a ~1 cm² contact area, assuming all the adhesive bonds break simultaneously.⁵ The fact that this is never observed is (mainly) due to surface roughness, and stress concentration at defect regions in the nominal contact region.

The influence of surface roughness on adhesion can be studied using the contact mechanics theory previously described by replacing the boundary condition $P(0,\upzeta )=0$ with the boundary condition $P(-\upsigma _{{{{\text {a}}}}},\upzeta )=0$, where $\upsigma _{{{{\text {a}}}}} (\upzeta )$ is the highest tensile stress at the interface when the contact is studied at the magnification $\upzeta$. Using the theory of cracks one can show that

$$\upsigma _{{{{\text {a}}}}} \approx \left[ \upgamma _{{{{\text {eff}}}}} (\upzeta ) E^{*} q_{0} \upzeta / 2\right] ^{1/2},$$

where $\upgamma _{{{{\text {eff}}}}} (\upzeta )$ is the effective interfacial energy (per unit surface area) in the (apparent) contact area observed at the magnification $\upzeta$. For an elastic solid with a rough surface in contact with a rigid solid with a flat smooth surface 2, $\upgamma _{{{{\text {eff}}}}} (\upzeta )$ is determined by^19,43,44

$$\upgamma _{{{{\text {eff}}}}} (\upzeta ) A(\upzeta ) = \Updelta \upgamma A(\upzeta _{1}) - U_{{{{\text {el}}}}} (\upzeta ),$$

where $\Updelta \upgamma = \upgamma _{1}+\upgamma _{2}-\upgamma _{12}$ is the change in the surface energy (per unit surface area) as two flat and smooth surfaces of the two materials are separated. $U_{{{{\text {el}}}}} (\upzeta )$ is the elastic energy stored at the interface when the roughness with wave number larger than $\upzeta q_{0}$ is included. One can write

$$U_{{{{\text {el}}}}} (\upzeta ) = E^{*} {\uppi \over 2} \int _{q_{0} \upzeta }^{q_{1}} {\text {d}}q \ q^{2} A(q) C(q).$$

The adhesion theory predicts that if the elastic modulus $E^{*}$ is large enough, or the surface roughness amplitude is large enough, then $\upgamma _{{{{\text {eff}}}}} (1) = 0$, which implies the pull-off force will vanish (i.e., there is no macroscopic adhesion). To illustrate this effect, in Figure 11, we show the measured work of adhesion w (which is proportional to the pull-off force) as a function of the number of contacts between a glass ball and a silicone rubber flat surface.⁴⁵ Note that in the adiabatic limit $w = \upgamma _{{{{\text {eff}}}}} (1)$. Results are shown for smooth and rough (sandblasted) glass balls in contact with smooth surfaces of stiff and soft silicone rubber. For the soft compound ($E=0.019 \ {{{\text {MPa}}}}$), the pull-off force increases by a factor of 2 when going from the smooth glass ball to the rough glass ball. This may be partly due to nonadiabatic effects (elastic instabilities at the asperity level), and partly to the increase in the area of real contact because of the surface roughness (the sandblasted ball has roughly double surface area as the not sandblasted ball). For the stiff rubber compound ($E=2.3 \ {{{\text {MPa}}}}$), we instead observe a reduction in the adhesion with a factor of ~10^-3 when going from the smooth ball to the sandblasted ball. This is due to the elastic energy stored at the interface during contact formation [the rubber surface must deform (bend) elastically to make contact with the glass surface], which is given back during pull-off and helps to break the interfacial bonds between the rubber and the glass ball. This same effect is the reason one cannot detect a pull-off force when removing a tire from a road surface. For very soft rubber compounds, as used in adhesive tapes, the stored elastic energy is so small that strong adhesion occurs even to very rough surfaces. It is possible to produce sticky materials from elastically stiff materials using hierarchical porous or fiber–plate constructions, which reduces the effective elastic modulus on all relevant length scales.^46,47 This is utilized in the adhesive pads of many insects and some lizards, which can adhere to very rough surfaces (e.g., stone walls).

Mixed lubrication

As a final application, we consider the sliding of an elastic cylinder (with radius R and length $L\gg R$) in a fluid on a rigid, randomly rough substrate occupying the xy-plane. This problem has important applications (e.g., for dynamical seals). We consider the simplest case of a Newtonian fluid with a constant viscosity $\upeta$, and neglect fluid flow and friction factors.^48,49 In this case, in a mean-field type of treatment, we write the pressure acting on the cylinder as the sum of the fluid and the asperity contact pressure $p_{0}(x)=p_{{{{\text {fluid}}}}}(x)+p_{{{{\text {cont}}}}}(x)$. The contact pressure is related to the average surface separation ${{\bar{u}}}(x)$ using the contact mechanics theory for dry surfaces so that, if the pressure is not too high or too low,

$$p_{{{{\text {cont}}}}} = \upbeta E^{*} {\text {e}}^{-{{\bar{u}}}/u_{0}}.$$

The fluid flow obey the Reynolds thin-film equation

$${{\text {d}}p_{{{{\text {fluid}}}}} \over {\text {d}} x} = 6 \upeta v_{0}\left( {1\over {{\bar{u}}}^{2}(x)}-{u^{*}\over {{\bar{u}}}^{3}(x)}\right) ,$$

where $u^{*}$ is determined so that the fluid pressure and the contact pressure give a normal force equal in magnitude to the external load acting on the cylinder:

$$\int _{-\infty }^{\infty } {\text {d}} x \ p_{0}(x) = {F_{{{{\text {N}}}}}\over L}.$$

The elastic deformation field is determined by the equations of elasticity:

$${{\bar{u}}}(x)=u_{0}+{x^{2}\over 2R} -{2\over \uppi E^{*}}\int _{-\infty }^{\infty }{\text {d}}x' \ p_{0} (x') {{{\text {ln}}}}\left| {x-x'\over x'}\right| .$$

Figure 12

The contact and fluid pressure distribution and the interfacial separation between an elastic cylinder sliding in the negative x-direction on a nominal flat substrate. The substrate has a self-affine fractal surface with the root-mean-square roughness $1 \, \upmu {{{\text {m}}}}.$

As an example, in Figure 12, we show the fluid pressure, the contact pressure, and the interfacial separation for a sliding speed in the mixed lubrication velocity region. Note that the surface separation is smallest on the exit side of the sliding contact as is typical for elastohydrodynamics applications.

Summary and conclusion

We have described the basic idea behind a multiscale contact mechanics theory for rough surfaces and presented several applications. The theory is accurate and very flexible and has been easily applied to many practical problems. In contrast to the classical Greenwood–Williamson contact mechanics theory,⁵⁰ which approximates all asperities by spherical bumps of equal radius and neglects the elastic coupling between the asperity contact regions, the present theory can be applied to systems with roughness extending over an arbitrary number of decades in length scales and includes the long-range elastic coupling between the different contact regions. Note that neglecting the elastic coupling result is a qualitatively wrong contact morphology¹² and huge error in most physical quantities, such as the leakage rate of seals, which depends on open flow channels at the contacting interface.²⁴