1 Introduction

The design of vehicle suspension systems (VSS) is concerned with finding a satisfactory trade-off between the conflicting criteria of vehicle ride comfort, quality of vehicle handling and road holding, within the limits of suspension travel (Hrovat, 1997; Pedro and Dahunsi, 2011). Research investigating the ability of passive vehicle suspension systems (PVSS), semi-active vehicle suspension systems (SAVSS), and AVSS to meet this demand has been very active since the 1950s (Guglielmino and Edge, 2004; Gao et al, 2006). This has been driven by the development of optimal control methods, improvements in computer processing capabilities, and increasing affordability of sensors and actuators (Hrovat, 1997; Guglielmino and Edge, 2004). Unlike PVSS and SAVSS, which have the ability only to dissipate force, AVSS are capable of introducing forces into the VSS. This positions AVSS better to address the trade-off, but at a higher cost in terms of energy and complexity (Williams, 1997; Fischer and Isermann, 2004). In addition, the best compromise must be achieved in the presence of the system’s nonlinearities and uncertainties (Pedro and Dahunsi, 2011).

Numerous AVSS control methods have been explored in previous studies. These include optimal control (Hassanzadeh et al, 2010), H 2 (Pedro, 2007), H ∞ (Chen et al, 2005; Du and Zhang, 2007; Ryu et al, 2008), H 2/H ∞ (Akcay and Turkay, 2009), linear parameter varying (LPV) (Fialho and Balas, 2002; Szaszi et al, 2002), sliding mode control (SMC) (Yoshimura et al, 2001), fuzzy logic control (FLC) (Du and Zhang, 2009a), backstepping control (Yagiz and Hacioglu, 2008), feedback linearization (FBL) (Chien et al, 2008; Fateh and Alavi, 2009), and various neural network (NN)-based control methods (Buckner et al, 2000; Dahunsi et al, 2009; Dahunsi and Pedro, 2010; Pedro and Dahunsi, 2011).

Simplicity and relative ease of tuning for adjustment of system control parameters (e.g., rise time, settling time, and overshoot), have led to extensive application of PID control in industry (Astrom and Hagglund, 2001; O′Dwyer, 2006; Cetin and Akkaya, 2010). Several authors within the field of AVSS research have applied PID control to quarter-car, half-car, and full-car AVSS (Kumar, 2008; Ekoru et al, 2011; Guclu, 2003). Furthermore, PID-based AVSS designs are used to set performance standards for other control methods such as NN-based control (Renn and Wu, 2007; Eski and Yildirim, 2009; Dahunsi and Pedro, 2010).

A lack of robustness in response to parameter variations and the requirement of high loop gains have motivated research on enhancing PID controller performance. Feng et al, 2003 demonstrated the use of a genetic algorithm (GA) to tune a combined PID/FLC for a half-car AVSS. Ji and Li 2009 employed FLC to adjust PID controller gains for an AVSS with hydraulic actuator dynamics. Dahunsi et al, 2010 and Zhao et al, 2011 overlaid PID controllers with a multi-layer perceptron (MLP) and radial basis function (RBF) NN controllers in feedforward, respectively, to quarter-car AVSS with servo-hydraulic actuator dynamics.

Past AVSS research was limited in terms of the amount of experimental validation. This is because the main focus was on calculation of the required control force, excluding the dynamics of the force generating actuators (Chantranuwathana and Peng, 2004; Sam and Hudha, 2006). Although many other types of actuators have been proposed in the literature, hydraulic actuators are the most common in AVSS owing to their rapid response time, high stiffness, superior power-to-weight ratio, low cost, and low heat dissipation during periods of sustained force generation (Dahunsi et al, 2009; Pedro and Dahunsi, 2011).

However, hydraulic actuators are highly nonlinear and prone to chattering in AVSS applications (Chantranuwathana and Peng, 2004). Moreover, since force generation in hydraulic actuators is highly coupled to the motion of the vehicle body (leading to the formation of backpressure), achieving the desired actuator force without force feedback is difficult (Sam and Hudha, 2006). Actuator force feedback stabilizes the hydraulic actuator ensuring that the desired force levels are attained, thereby improving vehicle ride comfort and road holding.

The need for hydraulic actuators with precision control for industrial applications such as automotives has warranted intensive study of their control. Marusak and Kuntanapreeda 2011 evaluated reference signal tracking performance of proportional (P), proportional-integral (PI), and model predictive controllers (MPC) for electro-hydraulic actuator force control. Guo et al, 2009 employed MLP NNs to adjust PID controller gains for position control of a servo-hydraulic system. Cetin and Akkaya 2010 developed a hybrid PID/FLC position control system for a hydraulic actuator.

Traditionally, force control in AVSS literature involves the use of an inner loop for actuator force feedback control and an outer loop for control of sprung mass displacement. Chantranuwathana and Peng 2004 studied adaptive force control of a quarter-car AVSS model using model reference adaptive control (MRAC). Sam and Hudha 2006 presented state feedback control of the outer loop together with PI control of the hydraulic actuator force in the inner control loop. Ji et al, 2007 applied a linear quadratic regulator (LQR) to sprung mass position control and time delay force control, to an electro-hydraulic quarter-car AVSS. Fateh and Alavi 2009 devised a quarter-car AVSS control scheme with FBL control of the hydraulic actuator and FLC position control of the sprung mass. Priyandoko et al, 2009 combined PI pneumatic actuator force control and PID sprung mass displacement control with NN-based active force control (AFC) and a skyhook to control a quarter-car AVSS.

Dynamic systems like AVSS contain model parameters, for example sprung mass loading, suspension damping and spring stiffness, and tyre damping and spring stiffness, whose exact values are uncertain. Hence, the need for a controller design which takes into account parametric uncertainty within acceptable bounds (Chen et al, 2005; Gao et al, 2006; Ryu et al, 2008; Du and Zhang, 2010).

This paper proposes PID control of a nonlinear half-car AVSS with hydraulic actuator dynamics. The control method consists of two control loops: an inner loop for PID hydraulic actuator force feedback control and an outer loop for suspension travel feedback control. Suspension travel is measured readily with devices like linear variable differential transformers (LVDT), prompting its selection as a controlled output variable in this work. This can also prevent suspension travel topping and bottoming (Du and Zhang, 2009b).

We also aimed to investigate the robustness of VSS in response to uncertainty in suspension damping. The performance of the developed PID-controlled nonlinear half-car AVSS with hydraulic actuator dynamics was compared with that of a nonlinear half-car PVSS with similar model parameters. Analysis was carried out in the frequency and time domains.

2 System model

2.1 Physical and mathematical modelling

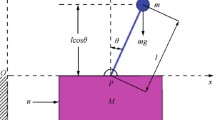
Fig. 1 illustrates a schematic of a half-car AVSS physical model, of sprung mass M s, pitch moment of inertia I θ , pitch angular displacement θ, and front and rear unsprung masses m uf and m ur, respectively. z c, z tf, and z tr are the vertical displacements of the sprung mass at the centre of gravity, the front tyre, and the rear tyre, respectively. The lengths between the front and rear axles and the vehicle centre of gravity are given by l f and l r, respectively. The front and rear suspensions travel are expressed as y f= z tf−( z c− l fsin θ) and y r= z tr−( z c+ l rsin θ), respectively. F ksf and F ksr are the forces due to the front and rear suspension springs, respectively. The forces due to the front and rear suspension dampers are F bsf and F bsr, respectively. The front and rear actuator forces are given by F af and F ar, respectively. F ktf and F ktr are the front and rear tyre spring forces, respectively, while the front and rear suspension damping forces are given by F btf and F btr, respectively.

Fig. 1
figure 1

Schematic of a half-car active vehicle suspension systems (AVSS) model for observing vehicle pitching motion

Full size image

Application of Newton’s second law of motion to the nonlinear half-car AVSS gives the governing equations of motion in state-space form as (Szaszi et al, 2002; Huang et al, 2010)

$$ \dot x = f\left( x \right) + g\left( x \right)u + pw,\,\,\,(1) $$
(1)

where x is the state vector, u is the control input vector, w is the disturbance input vector, f( x) is the system vector, g( x) is the control input matrix, and p is the disturbance input matrix.

$$ \begin{array}{*{20}c} {x = \left[ {z_{\text{c}} ,\theta ,z_{{\text{tf}}} ,z_{{\text{tr}}} ,\dot z_{\text{c}} ,\dot \theta ,\dot z_{{\text{tf}}} ,\dot z_{{\text{tr}}} ,{\text{P}}1_{\text{f}} ,{\text{P}}1_{\text{r}} ,x_{{\text{vf}}} ,x_{{\text{vr}}} } \right]^{\text{T}} } \\ { = \left[ {x_1 ,x_2 \cdots ,x_{12} } \right]^{\text{T}} ,} \\ \end{array} \,\,\,(2) $$
(2)
$$ u = \left[ {u_1 ,u_2 } \right]^{\text{T}} = \left[ {v_{\text{f}} ,v_{\text{r}} } \right]^{\text{T}} ,\,\,\,(3) $$
(3)
$$w = \left[ {w_{\text{f}} ,w_{\text{r}} ,\dot w_{\text{f}} ,\dot w_{\text{r}} } \right]^{\text{T}} ,\,\,\,(4) $$
(4)
$$ f\left( x \right) = \left[ {f_1 ,f_2 \cdots ,f_{12} } \right]^{\text{T}} .\,\,\,(5) $$
(5)

The output equation is given as

$$ y = \left[ {\begin{array}{*{20}c} {y_{\text{f}} } \\ {y_{\text{r}} } \\ \end{array} } \right] = h\left( x \right) = \left[ {\begin{array}{*{20}c} {x_3 - x_1 + l_{\text{f}} \sin x_2 } \\ {x_4 - x_1 + l_{\text{r}} \sin x_2 } \\ \end{array} } \right].\,\,\,(6) $$
(6)

The components of vector f( x) are given as

$$ f_1 = x_5 ,\,\,f_2 = x_6 ,\,\,f_3 = x_7 ,\,\,f_4 = x_8 ,\,\,\,(7)$$
(7)
$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {f_5 = \frac{1} {{M_{\text{s}} }}\left[ {{\text{ks}}_{\text{f}}^1 \left( {x_3 - x_1 + l_{\text{f}} \sin x_2 } \right) + {\text{ks}}_{\text{f}}^{{\text{nl}}} (x_3 - x_1 + l_{\text{f}} \sin x_2 )^3 } \right. + {\text{bs}}_{\text{f}}^1 \left( {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right)} \\ { - {\text{bs}}_{\text{f}}^{{\text{sym}}} \left| {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right| + {\text{bs}}_{\text{f}}^{{\text{nl}}} \left| {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right)} \\ \end{array} } \\ { - A_{{\text{hyd}}} x_9 + {\text{ks}}_{\text{r}}^1 \left( {x_4 - x_1 - l_{\text{r}} \sin x_2 } \right) + {\text{ks}}_{\text{r}}^{{\text{nl}}} \left( {x_4 - x_1 - l_{\text{r}} \sin x_2 } \right)^3 + {\text{bs}}_{\text{r}}^1 \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right)} \\ {\left. { - {\text{bs}}_{\text{r}}^{{\text{sym}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right| + {\text{bs}}_{\text{r}}^{{\text{nl}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right) - A_{{\text{hyd}}} x_{10} } \right],} \\ \end{array} \,\,\,(8) $$
(8)
$$ \begin{array}{*{20}c} {f_6 = \frac{1} {{I_\theta }}\left\{ { - l_{\text{f}} } \right.\left[ {{\text{ks}}_{\text{f}}^1 \left( {x_3 - x_1 + l_{\text{f}} \sin x_2 } \right) + {\text{ks}}_{\text{f}}^{{\text{nl}}} (x_3 - x_1 + l_{\text{f}} \sin x_2 )^3 } \right. + {\text{bs}}_{\text{f}}^1 \left( {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right)} \\ {\left. { - {\text{bs}}_{\text{f}}^{{\text{sym}}} \left| {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right| + {\text{bs}}_{\text{f}}^{{\text{nl}}} \left| {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right) - A_{{\text{hyd}}} x_9 } \right]} \\ { + \,l_{\text{r}} \left[ {{\text{ks}}_{\text{r}}^1 \left( {x_4 - x_1 + l_{\text{r}} \sin x_2 } \right) + {\text{ks}}_{\text{r}}^{{\text{nl}}} \left( {x_4 - x_1 - l_{\text{r}} \sin x_2 } \right)^3 + {\text{bs}}_{\text{r}}^1 \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right)} \right.} \\ {\left. {\left. { - {\text{bs}}_{\text{r}}^{{\text{sym}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right| + {\text{bs}}_{\text{r}}^{{\text{nl}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right) - A_{{\text{hyd}}} x_{10} } \right]} \right\}\cos x_2 ,} \\ \end{array} \,\,\,(9) $$
(9)
$$ \begin{array}{*{20}c} {f_7 = \frac{1} {{m_{{\text{uf}}} }}\left[ { - {\text{kt}}_{\text{f}} x_3 - {\text{bt}}_{\text{f}} x_7 - {\text{ks}}_{\text{f}}^1 \left( {x_3 - x_1 + l_{\text{f}} \sin x_2 } \right) - {\text{ks}}_{\text{f}}^{{\text{nl}}} (x_3 - x_1 - l_{\text{f}} \sin x_2 )^3 - {\text{bs}}_{\text{f}}^1 \left( {x_7 - x_5 + l_{\text{f}} x_6 \cos x_2 } \right)} \right.} \\ { + \left. {{\text{bs}}_{\text{f}}^{{\text{sym}}} \left| {x_7 - x_5 - l_{\text{f}} x_6 \cos x_2 } \right| - {\text{bs}}_{\text{f}}^{{\text{nl}}} \left| {x_7 - x_5 - l_{\text{f}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_7 - x_5 - l_{\text{f}} x_6 \cos x_2 } \right) + A_{{\text{hyd}}} x_9 } \right],} \\ \end{array} \,\,\,(10) $$
(10)
$$ \begin{array}{*{20}c} {f_8 = \frac{1} {{m_{{\text{ur}}} }}\left[ { - {\text{kt}}_{\text{r}} x_4 - {\text{bt}}_{\text{r}} x_8 - {\text{ks}}_{\text{r}}^1 \left( {x_4 - x_1 + l_{\text{r}} \sin x_2 } \right) + {\text{ks}}_{\text{r}}^{{\text{nl}}} \left( {x_4 - x_1 - l_{\text{r}} \sin x_2 } \right)^3 - {\text{bs}}_{\text{r}}^1 \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right)} \right.} \\ {\left. { + {\text{bs}}_{\text{r}}^{{\text{sym}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right| - {\text{bs}}_{\text{r}}^{{\text{nl}}} \left| {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right|^{1/2} \operatorname{sgn} \left( {x_8 - x_5 - l_{\text{r}} x_6 \cos x_2 } \right) + A_{{\text{hyd}}} x_{10} } \right],} \\ \end{array} \,\,\,(11) $$
(11)
$$ f_9 = \gamma \operatorname{sgn} \left[ {P_{\text{s}} - \operatorname{sgn} \left( {x_{11} } \right)x_9 } \right] \times \left| {P_{\text{s}} - \operatorname{sgn} \left( {x_{11} } \right)x_9 } \right|^{1/2} \,x_{11} - \beta x_9 - \alpha A_{{\text{hyd}}} \left( {x_5 - l_{\text{f}} x_{\text{6}} \cos x_2 - x_7 } \right),\,\,\,(12) $$
(12)
$$ f_{10} = \gamma \operatorname{sgn} \left[ {P_{\text{s}} - \operatorname{sgn} \left( {x_{12} } \right)x_{10} } \right] \times \left| {P_{\text{s}} - \operatorname{sgn} \left( {x_{12} } \right)x_{10} } \right|^{1/2} \,x_{12} - \beta x_{10} - \alpha A_{{\text{hyd}}} \left( {x_5 + l_{\text{f}} x_{\text{6}} \cos x_2 - x_8 } \right),\,\,\,(13) $$
(13)
$$ f_{11} = \dot x_{{\text{vf}}} = - x_{11} /\tau ,\,\,\,(14) $$
(14)
$$ f_{12} = \dot x_{{\text{vr}}} = - x_{12} /\tau ,\,\,\,(15) $$
(15)

where v f and v r are the front and rear control input voltages, respectively; ks lf and ks l r are linear and ks nlf and ks nlr are nonlinear spring coefficients for the front and rear suspensions, respectively; while bs lf and bs lr are linear, bs symf and bs symr asymmetric, and bs nlf and bs nlf nonlinear damping coefficients for the front and rear suspensions, respectively; ktf and ktr are the front and rear tyre stiffnesses, respectively; btf and btr are the front and rear tyre damping coefficients, respectively; and sgn() is the ‘signum’ function.

Eqs. (12)–(15) are the hydraulic actuator dynamics, where A hyd is the hydraulic piston area, and the pressure drop across the front and rear hydraulic actuator pistons are given by Plf and Plr, respectively; α, β and γ are hydraulic actuator parameters, τ is the hydraulic actuator time constant, and K vf and K vr are the servo valve gains for the front and rear actuators, respectively. The front and rear servo valve displacements are given by x vf and x vr, respectively.

A three-land four-way spool-valve double-acting hydraulic actuator (Fig. 2), was used in the AVSS. In Fig. 2, Q u and Q l are the hydraulic fluid flow rates to the upper and lower portions of the hydraulic cylinder, respectively, P s is the supply pressure, P r is the return pressure, and P u and P l are the hydraulic fluid pressures in the upper and lower portions of the cylinder, respectively.

Fig. 2
figure 2

Diagram of a double-acting hydraulic actuator

Full size image

The control input matrix, g( x), is given as

$$ g(x) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{K_{{\text{vf}}} }} {\tau }} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{{K_{{\text{vf}}} }} {\tau }} \\ \end{array} } \right]^{\text{T}} .\,\,\,(16) $$
(16)

The disturbance input matrix, p, is given as

$$ p = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & { - \frac{{{\text{kt}}_{\text{f}} }} {{m_{{\text{uf}}} }}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - \frac{{{\text{bt}}_{\text{f}} }} {{m_{{\text{uf}}} }}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & { - \frac{{{\text{kt}}_{\text{r}} }} {{m_{{\text{ur}}} }}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - \frac{{{\text{bt}}_{\text{r}} }} {{m_{{\text{ur}}} }}} & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}} \,\,\,(17) $$
(17)

2.2 Road input disturbance modelling

Eqs. (18) and (19) express the front and rear wheel input disturbances, w f and w r, respectively. The sinusoidal bump profile is illustrated in Fig. 3.

(18)
(19)

where a is the bump amplitude, V is the vehicle forward velocity, λ is the disturbance wavelength, t is the simulation time, and subscripts f and r denote the front and rear suspensions, respectively. t r0=1+ t d, where t d is the time delay between the front and rear wheels,

$$ t_{\text{d}} = (l_{\text{f}} + l_{\text{r}} )/V.\,\,\,(20) $$
(20)
Fig. 3
figure 3

Sinusoidal bump road input disturbance

(a) Disturbance time history; (b) Disturbance crosssectional dimensions

Full size image

The half-car, hydraulic actuator, and road input disturbance model parameters are given in Table 1 (Weber and Braaksma, 2000; Szaszi et al, 2002; Du and Zhang, 2009a).

Table 1
figure Tab1

Model parameters

Full size image

3 Performance specifications

The performance specifications used in this work are:

1. The closed-loops should be nominally stable, and the controller must have good command following and disturbance rejection.

2. The maximum allowable suspension travel, z max, should not exceed the limit given as

$$ \left| {y_i } \right| \leqslant z_{\max } ,\,\,\,(21) $$
(21)

where i∈(f, r), and z max is set to ±0.08 m.

3. The maximum allowable control voltage, u max, is expressed as

$$ \left| {u_i \left( t \right)} \right| \leqslant u_{\max } ,\,\,\,(22) $$
(22)

where u max is equal to ±10 V.

4. The maximum allowable controlled force, F a i , is given as

$$ \left| {F_{{\text{ai}}} } \right| \leqslant \pm M_{\text{s}} g,\,\,\,(23) $$
(23)

where g is the acceleration due to gravity, equal to 9.81 m/s2.

5. To maintain good road holding, the dynamic tyre load, F t i , should not exceed the static load, F statti (Gao et al, 2006),

$$ F_{{\text{t}}i} \leqslant F_{{\text{t}}i}^{{\text{stat}}} ,\,\,\,(24) $$
(24)

where

$$ F_{{\text{t}}i} = k_{{\text{t}}i} \left( {z_{{\text{t}}i} - w_i } \right) + b_{{\text{t}}i} \left( {\dot z_{{\text{t}}i} - \dot w_i } \right),\,\,\,(25) $$
(25)

and

$$ F_{{\text{t}}i}^{{\text{stat}}} = \left[ {\frac{{M_{\text{s}} l_i }} {{l_{\text{f}} + l_{\text{r}} }} + m_{{\text{u}}i} } \right].\,\,\,(26) $$
(26)

6. The root mean square (RMS) values of performance parameters given by Θ k, will be used to enable detailed performance comparison of the AVSS with the PVSS. For n simulation samples:

$$ \Theta _{{\text{RMS}}} = \sqrt {\frac{1} {n}\sum\limits_0^n {\left( {\Theta ^2 } \right)} } ,\,\,\,(27) $$
(27)

where

$$ \Theta = \left[ {y_{i,} F_{{\text{t}}i} ,\ddot z_{\text{c}} ,\ddot \theta ,u_i ,F_{{\text{a}}i} } \right]^{\text{T}} .\,\,\,(28) $$
(28)

7. ISO 2631–1:1997 frequency weighted RMS acceleration is the basis for evaluation of vehicle ride comfort. The AVSS model does not include vehicle seats, thus W k, the ISO 2631–1:1997 frequency weighting for acceleration input at the feet, was selected. A fifth order approximation of W k is expressed as (Zuo and Nayfeh, 2003):

$$ W_{\text{k}} \left( s \right) = \left( {87.72s^4 + 1138s^3 + 11336s^2 + 5453s + 5509} \right) \times \left( {s^5 + 92.6854s^4 + 2549.83s^3 + 25969s^2 + 81057s + 79783} \right)^{ - 1} .\,\,\,(29) $$
(29)

The weighted RMS acceleration, a RMSwi for n samples is given by

(30)

where the axis multiplication factor k axis=0.40, for vertical sprung mass acceleration along the z axis. A vibration-induced discomfort scale for various values of a RMSwi is given by the ISO 2631–1:1997 (Griffin, 2007).

4 Controller design

4.1 Control architecture

The control architecture (Fig. 4) consists of two control loops: the outer control loop serves to control suspension travel, while the inner PID force control loop ensures that the desired control force is achieved by the hydraulic actuator. R f( t) and R r( t) are the front and rear suspension travel reference signals, respectively.

Fig. 4
figure 4

Control architecture

Full size image

4.2 PID suspension travel control loop design

The structure of the PID controller structure has been applied widely (Gao, 2002; Astrom and Hagglund, 2004; Hanafi, 2010). To perform suspension travel regulation, the suspension travel reference signal, R i is set to zero so that the error between the reference and the suspension travel tends to zero as t→∞ (Gao, 2002). The outer PID suspension travel loop generates the desired actuator force reference signal F airef, given in Eq. (31).

$$ F_{{\text{airef}}} = K_{\text{p}} e_i \left( t \right) + K_{\text{I}} \int {e_i \left( t \right){\text{d}}t + K_{\text{D}} \frac{{{\text{d}}e_i \left( t \right)}} {{{\text{d}}t}},\,\,\,(31)} $$
(31)
$$ e_i \left( t \right) = R_i - y_i ,\,\,\,(32) $$
(32)

where K P is the proportional gain, K I is the integral gain, K D is the derivative gain, subscript i represents either the front or rear suspension, i∈(f, r), and e i is the error signal. The PID controller gains for the suspension travel loop are listed in Table 2. These gains were obtained by applying the Ziegler-Nichols PID controller gains tuning method.

Table 2
figure Tab2

PID suspension travel control loop tuning parameters

Full size image

4.3 PID force control loop design

The PID force control loop is shown in Fig. 5 in which u i is the hydraulic actuator control voltage.

Fig. 5
figure 5

Inner PID force feedback control loop

Full size image

This control input signal is generated by minimizing e i , the error between F airef and the actual actuator force F a i given in Eq. (33):

$$ e_i \left( t \right) = F_{{\text{airef}}} - F_{{\text{a}}i} ,\,\,\,(33) $$
(33)

and u i is then calculated using PID control (Gao, 2002; Astrom and Hagglund, 2004; Hanafi, 2010):

$$ u_i = K_{\text{p}} e_i \left( t \right) + K_{\text{I}} \int {e_i \left( t \right){\text{d}}t + K_{\text{D}} \frac{{{\text{d}}e_i \left( t \right)}} {{{\text{d}}t}}.\,\,\,(34)} $$
(34)

A saturation block was placed in front of the controller output to ensure that the control voltage limits (|u i ( t)|≤10 V) were not exceeded in the MATLAB/Simulink implementation. The PID controller gains for the inner force control loop are listed in Table 3. These controller gains were also obtained using the Ziegler-Nichols PID controller tuning rules.

Table 3
figure Tab3

PID force control loop tuning parameters

Full size image

5 Simulation results and discussion

The half-car AVSS and PVSS models were built in the MATLAB/Simulink environment. The ordinary differential equation (ODE)-3 (Bogacki-Shampine) fixed step solver was selected for the simulations. To enable observation of all model dynamics, the sampling time was set to T s=0.0001 s, smaller in magnitude than the fastest half-car AVSS model dynamics (Dahunsi and Pedro, 2010). Since the AVSS and PVSS models do not have multiple sampling times, the tasking mode for periodic sampling times was set to “Single Tasking”.

A chirp road input disturbance signal of amplitude ±15 mm (Sammier et al, 2003) with frequency increasing from 0–100 Hz (over a simulation period of 100 s), was applied to perform a frequency sweep on the AVSS and PVSS (Savaresi et al, 2010). Spectral analysis was performed on the AVSS and PVSS model outputs with the MATLAB Welch algorithm/spectral estimator. Optimal frequency response plots were obtained by using the “Hamming” window setting, a segment length of N/100 (where N is the total number of samples) and a percentage overlap of 214 (The MathWorks, Inc., 2001).

Frequency responses are plotted for Δ=±30% variation in the linear, nonlinear, and asymmetric damping coefficients in Section 5.1 (Chen et al, 2005). The time domain response plots for the AVSS and PVSS traversing over a sinusoidal bump road input disturbance are given in Section 5.2 for ±30% variation in respectively (Chen et al, 2005).

5.1 Variation of suspension damping coefficients in the frequency domain

Figs. 6–11 show the AVSS and PVSS front suspension travel, rear suspension travel, front dynamic tyre force, rear dynamic tyre force, sprung mass acceleration, and pitch angular acceleration power spectral density (PSD) plots, respectively, for Δ=±30% variation in bs l i , bs nl i , and bs sym i about their nominal values. The AVSS response was more robust to variation in suspension damping coefficients in the region below 4 Hz and the region around the wheel-hop frequency (≈12 Hz), than that of the PVSS. The PVSS peak at the wheel-hop frequency was higher than that of the AVSS. Between 4–8 Hz and above 20 Hz, both the AVSS and PVSS produced similar performance.

Fig. 6
figure 6

Front suspension travel PSD for AVSS (a) and PVSS (b)

Full size image
Fig. 7
figure 7

Rear suspension travel PSD for AVSS (a) and PVSS (b)

Full size image
Fig. 8
figure 8

Front dynamic tyre force PSD for AVSS (a) and PVSS (b)

Full size image
Fig. 9
figure 9

Rear dynamic tyre force PSD for AVSS (a) and PVSS (b)

Full size image
Fig. 10
figure 10

Sprung mass acceleration PSD for AVSS (a) and PVSS (b)

Full size image
Fig. 11
figure 11

Pitch angular acceleration PSD for AVSS (a) and PVSS (b)

Full size image

5.2 Variation of suspension damping coefficients: time domain example

Table 4 (p.410) shows the RMS values obtained as the AVSS and PVSS traversed the sinusoidal bump road input disturbance given in Section 2.2 for Δ= ±30% variation in bs l i , bs nl i , and bs sym i about their nominal values.

Table 4
figure Tab4

RMS values for Δ=±30% variation in bs l i , bs nl i , bs sym i about their nominal values

Full size image

FST: front suspension travel; RST: rear suspension travel; SMA: sprung mass acceleration; PAA: pitch angular acceleration

The AVSS and PVSS front suspension travel time histories are shown in Figs. 12a and 12b, respectively. The AVSS was more robust than the PVSS in response to variation in suspension damping coefficients. The figures also show that the AVSS front suspension travel minimum and maximum peak values were considerably lower than those of the PVSS. The RMS front suspension travel performance of the AVSS was considerably better than that of the PVSS, although the AVSS performance deteriorated with increasing suspension damping (Table 4). The AVSS and PVSS did not exceed the ±0.08 m suspension travel limit set in Section 3.

Fig. 12
figure 12

Front suspension travel time history for AVSS (a) and PVSS (b)

Full size image

Figs. 13a and 13b show the rear suspension travel time histories for the AVSS and PVSS, respectively. The peak rear suspension travel values were lower for the AVSS than for the PVSS. The AVSS performance in terms of reducing RMS suspension travel varied between 33.00% at minimum suspension damping and 28.77% at maximum suspension damping. Thus, there was a drop in performance as the suspension damping increased. The ±0.08 m suspension travel limit set in Section 3 was not exceeded by either the AVSS or the PVSS.

Fig. 13
figure 13

Rear suspension travel time history for AVSS (a) and PVSS (b)

Full size image

The front dynamic tyre force time histories for the AVSS and PVSS are shown in Figs. 14a and 14b, respectively. The AVSS front dynamic tyre force was more robust to variation in the suspension damping coefficients than the PVSS. These figures also show that the AVSS produced lower peak front dynamic tyre force magnitudes than the PVSS. Furthermore, the peak front dynamic tyre forces for both the AVSS and PVSS did not exceed the front dynamic tyre force limits specified in Section 3. The AVSS performance, in terms of reducing RMS front dynamic tyre force, deteriorated with increasing suspension damping compared with PVSS performance (Table 4).

Fig. 14
figure 14

Front dynamic tyre force time history for AVSS(a) and PVSS (b)

Full size image

Figs. 15a and 15b show the rear dynamic tyre force time histories for the AVSS and PVSS, respectively. The AVSS rear dynamic tyre force was less sensitive to variation in the suspension damping, than the PVSS. The AVSS peak rear dynamic tyre forces were lower than those of the PVSS. In addition, the rear dynamic tyre force limits specified in Section 3 were not exceeded by either the AVSS or the PVSS. Table 4 shows that the PVSS RMS rear dynamic tyre force was lower than that of the AVSS. However, the AVSS performance improved with increasing suspension damping.

Fig. 15
figure 15

Rear dynamic tyre force time history for AVSS (a) and PVSS (b)

Full size image

Figs. 16a and 16b show the sprung mass acceleration time histories for the AVSS and PVSS, respectively. The AVSS attenuated the sprung mass acceleration oscillation about 1.5 s faster than the PVSS, at the minimum suspension damping ( Δ= −30%). The AVSS peak sprung mass acceleration values were lower than those of the PVSS. The AVSS reduced the ISO-weighted RMS acceleration compared with the PVSS. However, Table 5 shows that the AVSS performance degraded with increasing suspension damping (from 31.81% improvement at the minimum damping, to 15.61% improvement at the maximum damping). Table 5 also shows that the AVSS and PVSS obtained acceleration values within the ISO 2631–1:1997 range for the “Not uncomfortable” level of discomfort.

Fig. 16
figure 16

Sprung mass acceleration time history for AVSS (a) and PVSS (b)

Full size image
Table 5
figure Tab5

Weighted RMS acceleration, a RMSwi , and discomfort levels for the PVSS and AVSS

Full size image

Figs. 17a and 17b show the pitch angular acceleration time histories for the AVSS and PVSS, respectively. The AVSS was more robust in response to variation in suspension damping coefficients than the PVSS. The AVSS attenuated the pitch angular acceleration oscillation about 1 s faster than the PVSS for Δ=−30%. However, the AVSS peak pitch angular acceleration values were higher than the corresponding PVSS values. The percentage reduction in RMS pitch angular acceleration by the AVSS compared with the PVSS deteriorated with increasing suspension stiffness; from 20.76% at Δ=−30% to −5.39% at Δ=30% (Table 4).

Fig. 17
figure 17

Pitch angular acceleration time history for AVSS (a) and PVSS (b)

Full size image

Figs. 18a and 18b show the actuator force time histories for the front and rear suspension actuators, respectively. The AVSS maintained peak actuator force levels much lower than the limits specified in Section 3 for the duration of the simulation. The RMS actuator forces for the front and rear suspension actuators reduced with increasing suspension damping (Table 4).

Fig. 18
figure 18

Actuator force time history for AVSS (a) and PVSS (b)

Full size image

5.3 Effect of the inner force control loop on AVSS performance

In this section, the effect of the inner force control loop on AVSS performance is investigated. An AVSS with both an inner PID force control loop and an outer PID suspension travel control loop was compared with a second AVSS without the inner force control loop. The PID controller gains of the outer suspension travel for the second AVSS remained the same as those given in Table 2. The sprung mass acceleration frequency and time domain responses of an AVSS without the PID force control loop are plotted against those of an AVSS with the PID force control loop. Only nominal suspension damping was considered.

Fig. 19a shows that the AVSS with PID force control performed better than the AVSS without PID force control over the frequency range plotted. Fig. 19b shows that the AVSS with force control was able to attenuate the sprung mass oscillation due to the road input disturbance after about 2 s. The AVSS without force control was unable to stabilize the hydraulic actuator, therefore the sprung mass oscillation continued beyond the duration of the simulation.

Fig. 19
figure 19

Comparison of AVSS sprung mass acceleration response with and without force control

(a) PSD; (b) Time history

Full size image

6 Conclusions

1. This paper described the development of controllers for a nonlinear half-car AVSS with hydraulic actuator dynamics, by application of PID-based controls, an outer PID suspension travel control loop, and an inner PID force control loop. A nonlinear half-car PVSS was developed for performance comparisons.

2. Performance specifications were outlined for controller performance, physical constraints (control input voltage, hydraulic actuator force output and suspension travel limitations), road holding (to prevent tyre lift off), and ride comfort (based on ISO 2631–1:1997).

3. Results of performance comparisons between the AVSS with the PVSS in the presence of uncertainties due to variations in suspension damping were given based on frequency domain analysis and an example in the time domain.

4. In the frequency domain analysis, a frequency sweep was used to obtain frequency response data from the various outputs of the nonlinear AVSS and PVSS models.

5. The frequency domain results indicated that the AVSS was less sensitive than the PVSS to variation in suspension damping in the low frequency regions (<4 Hz), between 4–8 Hz, and around the wheel-hop frequency for all the model outputs.

6. Above 20 Hz, both the AVSS and PVSS frequency responses to uncertainties in damping were similar.

7. Time domain results confirm the robustness of the AVSS in the presence of uncertainties in damping, in the low frequency region.

8. The AVSS provided a better compromise between vehicle ride comfort and road holding than the PVSS, without exceeding suspension travel, control input voltage, and hydraulic actuator force output constraints.

9. The need for hydraulic actuator force control to stabilize the actuator, thus enhancing AVSS performance, was demonstrated.