1 Introduction

Soft surrounding rock often shows serious strain softening behavior during the excavation of roadways located in weak strata composed of Jurassic or Cretaceous soft rock. The degradation of mechanical performance caused by softening behavior results in a sharp drop in a roadway’s bearing capacity. Therefore, the mechanical behavior of soft rock at the post-peak stage plays a key role in the stability of underground rock structures. The decrease in bearing capacity of soft rock is, in essence, the result of the accumulation and fast development of internal damage at the strain softening stage. Hence, an understanding of the evolution laws of strength parameters of soft rock at the post-peak stage is needed urgently to improve significantly roadway safety and the precision of numerical simulations.

It is generally acknowledged that the rock surrounding underground engineering exhibits strain softening properties (Hoek and Brown, 1997). This behavior is more significant in the special soft rock in western mining areas of China due to their poor characteristics of low strength, weak cementation, and ease of weathering. The stress-strain curve of soft rock under compression contains the evolution information of mechanical parameters in the failure process. Researchers have put forward different methods to study the strain softening behavior of soft rock. Firstly, some indoor experiments were adopted. For example, Zhang et al. (2013) proposed an elastoplastic model for red sandstone based on the tri-axial test, and obtained the evolution laws of compression strength by defining a plastic internal variable. To simulate the real failure process of surrounding rock around a deep roadway, Niu et al. (2012) designed a stress evolution path for sandy mudstone by carrying out a cyclic loading experiment which showed that the strength parameters at the post-peak stage decreased at the exponential status. Based on a direct shear test, Martin and Chandler (1994) and Martin (1997) analyzed the variation laws of strength parameters of irregular lumps of rock collected from conventional compression fractures, and then discussed the fields of application for bond-weakening and friction-hardening models. Although these experimental results are intuitive and persuasive, they lack universality due to the limitations of variation in experimental conditions and rock properties. Secondly, some strain softening models were built based on the macro effects of soft rock by employing the complete theory of continuum mechanics. Zdenek and Bazant (1984) proposed an exponent-form plastic strain softening model, and established the relationship between equivalent stress and equivalent plastic strain. Based on the Weibull probability distribution theory of micro-unit strength and taking the probabilistic damage as variable, Cao et al. (2007) developed a statistical damage constitutive model for rock mass which considered the random distribution of inner defects. The main shortcoming of the above theoretical research is that the results were based on some simplifications which limit their applicability to actual conditions. In view of this, according to the plastic potential theory and test data from tri-axial compression, Zhang et al. (2008) studied the relationship between strength parameters and strain softening parameters of granite by fitting the subsequent yield surface. On this basis, Lu et al. (2010) introduced the concept of generalized cohesion and the friction angle to express the subsequent yield surface. They discussed the attenuation rules of strength parameters of soft rock considering the confining pressure effect, and finally carried out a numerical verification. Joseph (2000) and Joseph and Barron (2003) derived the relationship between the tangent modulus and strain at the post-peak stage, and obtained the stress-strain curve by characterizing the friction angle as a function of the strain. Yu et al. (2012) put forward a degradation angle to describe the brittle feature after the peak point, and established a strain softening model which could accurately describe the relationship between the brittle behavior and the confining pressure of a rock sample. Thirdly, some numerical calculation methods were proposed to clarify the effect of strength degradation in soft rock. From the numerical results of tri-axial compression, Wang et al. (2010) and Han et al. (2013) drew the conclusion that the stress-strain curve usually displayed nonlinear characterization even if the strength parameters decreased linearly with plastic strain. According to the plastic potential theory, Li et al. (2011) established a strain softening model considering the degradation of deformation modulus and strength parameters at the post-peak stage, and carried out its further development and verification in FLAC3D. Chen et al. (2010) obtained a warning deformation value of rock failure based on a strength reduction method which considered the attenuation of the deformation modulus, cohesion and tensile strength in the failure area of the surrounding rock, and presented a new method for the rapid determination of the stability condition. Based on meso-damage mechanics, Lei et al. (2013) established an equivalent unloading numerical model for soft rock in realistic failure process analysis (RFPA), and discussed the attenuation law of stiffness and strength parameters in the unloading process. These results were all based on the assumption that the attenuation of mechanical parameters obeyed a general principle, which made the conclusions inaccurate. In addition to the above findings, Wang et al. (2009) discussed the stiffness degradation phenomenon in the local shear band from the strain localization angle. Although the results are very helpful for exploring the internal damage mechanism of soft rock, they are difficult to apply in engineering fields.

According to the results of massive cyclic loading experiments (Fang and Harrison, 2001; Isik et al., 2008; Palchik, 2011; Flora and Lirer, 2013), the elastic modulus of soft rock shows remarkable behavior of gradual degradation at the post-peak stage in the process of tri-aixal compression. Despite its apparent importance in determining the mechanical behavior of soft rock, previous studies focused mainly on the attenuation law of strength parameters, which assumed that the elastic modulus at the post-peak stage was constant. This is obviously unreasonable. Currently, there is not enough research trying to establish and understand the relationship between modulus damage and strength attenuation. To understand better the internal connection, in this paper, we present an evolution model for the attenuation law of strength parameters of soft rock at the failure stage which considers stiffness degradation. The model is verified by comparisons between a numerical simulation and an indoor test. The conclusions aim to provide theoretical guidance for studying the mechanisms affecting roadway stability in soft rock strata.

2 Stiffness degradation model for soft rock

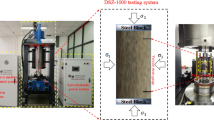
Fig. 1 shows the different stress-strain relations of soft mudstone samples, collected from the Xinjiang Ili mining area of China, under different confining pressures. Evidently, the samples were very sensitive to confining pressures whether the deformation was at the pre-peak stage or the post-peak stage. The samples exhibited residual strength and apparent shear failure even under low confining pressure, a behavior entirely different from that of hard rock.

Fig. 1
figure 1

Stress-strain relations of mudstone under tri-axial compression with different confining pressures

Full size image

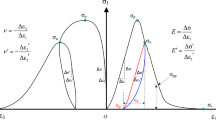
From the analysis of the entire failure process of mudstone, its damage threshold point should be at the yield point (Fig. 2). The evolution laws of stiffness and strength parameters lack regularity at the yield stage due to the low-level damage and relatively complex development of internal micro-cracks in the rock sample. After peak point B, failures in the sample expand to a high level due to the extension of a penetrative cranny, and the sample suffers concentration damage. The unloading modulus E s is much lower than the elastic modulus E 0 at the pre-peak stage if the sample is unloaded at any point K at the post-peak stage (Fig. 2). This is because of the stiffness degradation of soft rock at the post-peak stage.

Fig. 2
figure 2

Stiffness degradation of mudstone under tri-axial compression

Full size image

The yield step before the peak point could be treated as an extension of the elastic range due to the relatively short feature of yield stage AB (Fig. 2). Therefore, the stress-strain curve of soft mudstone was simplified as a tri-linear model (Fig. 3) according to the plastic strain softening model proposed by Toshikazu (1981). Stage OB includes pressurization, closure, and the development of internal micro-cracks. In stage BC, the stiffness and strength of the rock sample gradually decrease due to the extension and penetration of cracks. Stage CD represents the residual stage. To consider the effect of confining pressure, an equivalent stress σ e=σ 1−2νσ 3 was defined as vertical coordinates without considering the change in Poisson’s ratio ν. In fact, the equivalent stress σ e is equal to the superposition of the axial stress σ 1 and a constant under a specified confining pressure, so the curve shapes of σ e−ε 1 and σ 1−ε 1 are consistent with each other.

Fig. 3
figure 3

Simplified tri-linear strain softening model of mudstone

Full size image

Let the elastic modulus at the pre-peak stage and post-peak stage be E 0 and E s, respectively. Here, we introduce a softening modulus α, which denotes the softening degree at the post-peak stage. The relationship E c=E 0 should be satisfied without considering the stiffness attenuation at the yield stage, where E c represents the unloading modulus at the peak point. Through the introduction of a stiffness degradation coefficient ω with a scope of [0, 1], the unloading elastic modulus E s of point P at the post-peak stage can be defined as follows:

$${E_{\rm{s}}} = (1 - \omega ){E_{\rm{c}}} + \omega {E_{\rm{r}}},$$
(1)

where E r represents the elastic modulus at the residual stage. Equalities E s=E 0 and E s=E r hold when ω is set as 0 and 1, respectively. Actually, E s is a function of ω under a specified confining pressure. Here, ε e and ε p denote the elastic strain and plastic strain of point P, respectively.

3 Evolution model for strength parameters of soft rock

The equation for the post-peak stage can be expressed as

$${\sigma _1} = {\sigma _{1c}} - \alpha ({\varepsilon _1} - {\varepsilon _{{\rm{1c}}}}),$$
(2)

where σ 1c and σ 1 represent the axial stress at the peak point and point P, respectively. Suppose that ε 1c and ε 1 are the axial strains at the peak point and at point P, respectively. From Fig. 3, the total axial strain can be derived as

$${\varepsilon _1} = {\varepsilon _{{\rm{1e}}}} + {\varepsilon _{{\rm{1p}}}},$$
(3)

where ε 1e and ε 1p stand for the elastic strain and plastic strain, respectively. For conventional tri-axial compression, the elastic strain ε 1e of point P can be calculated as

$${\varepsilon _{1{\rm{e}}}} = {\sigma _{\rm{e}}}/{E_{\rm{s}}},$$
(4)

thus the plastic strain should be

$${\varepsilon _{1{\rm{p}}}} = {\varepsilon _{1{\rm{c}}}} + {{{\sigma _{1{\rm{c}}}} - {\sigma _1}} \over \alpha} - {{{\sigma _{\rm{e}}}} \over {{E_{\rm{s}}}}}.$$
(5)

Regardless of stiffness degradation, the elastic strain ε 1e in the post-peak stage can be calculated as ε 1e ′=σ e/E 0. According to the relationship E s<E 0, it is evident that the plastic strain decreases with the stiffness attenuation caused by the damage mechanism due to ε 1e<ε 1e ′. Actually, the deformation of soft rock is a coupled process of damage failure and a plastic mechanism. Suppose the stress state at the post-peak stage meets the Mohr-Coulomb yield criterion. Namely, all stress points are on yield surfaces Φ, which can be expressed as

$$\Phi = {\sigma _1} - \xi {\sigma _3} - 2C\sqrt \xi,$$
(6)

where ξ=(1+sinφ)/(1−sinφ), C and φ denote the cohesion and friction angle, respectively, of the subsequent yield surface in the strain softening stage. It is clear that the cohesion C and friction angle φ are not constant due to the degradation of stiffness and strength during the post-peak stage. By selecting the equivalent plastic shear strain ε ps as a softening parameter, cohesion C and friction angle φ should be the function of the confining pressure σ 3 and ε ps. That is, the stress state on the subsequent yield surface should satisfy

$${\sigma _1} - \xi ({\sigma _3},{\varepsilon ^{{\rm{ps}}}}){\sigma _3} - 2C({\sigma _3},{\varepsilon ^{{\rm{ps}}}})\sqrt {\xi ({\sigma _3},{\varepsilon ^{{\rm{ps}}}})} = 0.$$
(7)

Without considering the effect of intermediate principal stress σ 2, the equivalent plastic shear strain ε ps can be calculated as

$${\varepsilon ^{{\rm{ps}}}} = \sqrt {{1 \over 2}\left[ {{{({\varepsilon _{1{\rm{p}}}} - {\varepsilon _{{\rm{mp}}}})}^2} + {{({\varepsilon _{3{\rm{p}}}} - {\varepsilon _{{\rm{mp}}}})}^2} + \varepsilon _{{\rm{mp}}}^2} \right]} \;,$$
(8)

where ε mp is the average plastic strain, which can be obtained from ε mp=(ε 1p+ε 3p)/3.

Let η be the dialtancy gradient according to the irrelative plastic flowing law. The lateral strain ε 1p can be calculated as

$${\varepsilon _{3{\rm{p}}}} = - \eta {\varepsilon _{1{\rm{p}}}}.$$
(9)

When η=1, no dialtancy effect exists. Only if η>1, will a dialtancy effect be produced in the softening stage. The dialtancy gradient η should be the function of the confining pressure, namely η=η(σ 3). According to the simultaneous solution of Eqs. (8) and (9), the equivalent plastic strain at the post-peak stage can be changed to

$${\varepsilon ^{{\rm{ps}}}} = {\rm N}{\varepsilon _{1{\rm{p}}}},$$
(10)

where

$$N = \sqrt {{{1 + \eta + {\eta ^2}} \over 3}}.$$

Based on Eqs. (3) and (4), the relationship between strength and plastic strain in the softening stage can be established as follows:

$${\sigma _1} = {{1 + {\alpha \over {{E_0}}}} \over {1 + {\alpha \over {{E_{\rm{s}}}}}}}{\sigma _{1c}} - {\alpha \over {1 + {\alpha \over {{E_{\rm{s}}}}}}}{\varepsilon _{1p}} + 2\nu {{{\alpha \over {{E_{\rm{s}}}}} - {\alpha \over {{E_0}}}} \over {1 + {\alpha \over {{E_{\rm{s}}}}}}}{\sigma _3}.$$
(11)

Let C 0 and φ 0 be the initial cohesion and friction angle respectively, of the rock sample. When the sample is loaded to peak point, only the initial yield is produced, and the initial yield surface should satisfy

$${\Phi _0} = {\sigma _{1{\rm{c}}}} - {\xi _0}{\sigma _3} - 2{C_0}\sqrt {{\xi _0}} = 0,$$
(12)

where ξ0=(1+sinφ 0)/(1-sinφ 0).

From Eq. (12), the axial stress σ 1c is calculated as

$${\sigma _{1{\rm{c}}}} = {\xi _0}{\sigma _3} + 2{C_0}\sqrt {{\xi _0}}.$$
(13)

Thus, by jointly solving Eqs. (7), (10), (11), and (13), the evolution equations of strength parameters are determined as

$$\varphi = {\rm{arcsin}}{{{A_1}{\xi _0} + {A_2} - 1} \over {{A_1}{\xi _0} + {A_2} + 1}},$$
(14)
$$C = {A_1}{C_0}\sqrt {{{{\xi _0}} \over {{A_1}{\xi _0} + {A_2}}}} - {{{A_3}{\varepsilon _{{\rm{ps}}}}} \over {{\rm N}\sqrt {{A_1}{\xi _0} + {A_2}}}},$$
(15)

where

$${A_1} = {{1 + {\alpha \over {{E_0}}}} \over {1 + {\alpha \over {{E_{\rm{s}}}}}}},\;{A_2} = 2\nu {{{\alpha \over {{E_{\rm{s}}}}} - {\alpha \over {{E_0}}}} \over {1 + {\alpha \over {{E_{\rm{s}}}}}}},\;{A_3} = {\alpha \over {2\left( {1 + {\alpha \over {{E_{\rm{s}}}}}} \right)}}.$$

The internal friction angle reflects mainly the friction strength characteristics of soft rock, and its evolution law at the post-peak stage is dominated by the instantaneous stress state and damage mechanism. The attenuation law of cohesion is related to the plastic deformation behavior of soft rock, in addition to the stress level and damage state. Without considering the stiffness degradation, namely E s=E 0, the model factors are determined as A 1=1, A 2=0, and A 3 depends only on the softening modulus α. In this case, the friction angle at the softening stage will keep constant, and the cohesion will decrease in linear rule. This result is consistent with the conclusions obtained by Zhang et al. (2008).

4 Engineering case

The mechanical parameters of soft mudstone collected from the Ili mining area were measured as follows, by a tri-axial compression experiment: initial cohesion C 0=4.5 MPa, initial friction angle φ 0=44°, and Poisson’s ratio ν=0.25. Calculation results for other model parameters are listed in Table 1.

Table 1 Test results of soft mudstone
Full size table

Fig. 4 shows the calculation results of evolution laws of the friction angle under different confining pressures according to Eq. (14). Clearly, the degradation rate of the friction angle under uni-axial compression is significantly higher than that under tri-axial compression condition. Due to the characteristic of weak cementation, the friction angle of mudstone decreases to 20° when the confining pressure is set at 0 MPa. As the confining pressure increases, the attenuation rate decreases gradually and remains relatively constant when the confining pressure increases to 5 MPa. The percentages of the residual friction angle in relation to its initial value are 45.3%, 78.3%, 82.2%, 85.7%, 94.6%, and 98.0%, respectively, with confining pressure increasing from 0 MPa to 5 MPa.

Fig. 4
figure 4

Evolution laws of the friction angle under different confining pressures

Full size image

The attenuation laws of cohesion at the post-peak stage under different confining pressures according to Eq. (15) are shown in Fig. 5. As for the friction angle, the cohesion decreases rapidly under uni-axial compression. With increasing confining pressures, the attenuation rate seems to head downwards. Even if the confining pressure is increased to 5 MPa, cohesion of soft mudstone exhibits an obvious attenuation tendency. The percentages of residual cohesion in relation to its initial value are 45.3%, 72.2%, 74.2%, 75.9%, 84.0%, and 87.1%, respectively, when the confining pressure is increased from 0 MPa to 5 MPa.

Fig. 5
figure 5

Evolution laws of cohesion under different confining pressures

Full size image

Fig. 6 shows a comparison of residual strength parameters of soft mudstone under different confining pressures. The residual cohesion and friction angle improve significantly with increasing confining pressure. Their growth rates under high confining pressure tend to be stable. The residual friction angle approaches its initial value before damage occurs.

Fig. 6
figure 6

Residual strength parameters under different confining pressures

Full size image

The relationship between the residual friction angle φ r and the confining pressure σ 3 is established by data regression, as follows:

$${\varphi _{\rm{r}}} = 41.9 - 21.5{\rm{exp(}} - 0.7{\sigma _3}{\rm{)}}.$$
(16)

By adopting the same practice, the regression equation for residual cohesion C r is calculated from

$${C_{\rm{r}}} = {\rm{exp}}\left( {{\rm{15}}{\rm{.2}} - {{0.46} \over {{\sigma _3} + 0.67}}} \right).$$
(17)

For further analysis of the corresponding relationships between degradation stiffness and strength parameters with confining pressure and equivalent plastic strain, a contour plot for the evolution laws of mechanical parameters at the post-peak stage was drawn (Fig. 7). The results were acquired by 3D data fitting in MATLAB.

Fig. 7
figure 7

Evolution contours of mechanical parameters of soft mudstone under different confining pressures Contour plot for stiffness degradation (a), the evolution of cohesion (b), and the evolution of the friction angle (c)

Full size image

The change tendency of the evolution contour plot of elastic modulus at the post-peak stage is shown in Fig. 7a. The contour value alters sharply under low confining pressure (≤3 MPa), which indicates that the stiffness has severely decreased. For instance, the percentage of residual stiffness in relation to its initial value is only 20%, 54%, 55%, and 60% when the confining pressure is set at 0 MPa, 1 MPa, 2 MPa, and 3 MPa, respectively. However, if σ 3 is increased to 4 MPa and 5 MPa, it increases to 75% and 78%, respectively. The change tendency of the evolution contour plot reveals the significant effect of confining pressure on stiffness degradation and plastic deformation.

Figs. 7b and 7c show the evolution contour plots of the cohesion and friction angle, respectively, with equivalent plastic strain under different confining pressures. Under the action of low confining pressure, the strength parameters decrease dramatically with equivalent plastic strain at the post-peak stage. Results of equivalent plastic strain show significant differences under different confining pressures. When σ 3>3 MPa, the contour plot changes smoothly, which represents a low attenuation rate of strength parameters.

5 Model verification

To verify the advantages of the model proposed in this work, an indoor tri-axial compression experiment and corresponding numerical simulation were carried out and the results were compared. The strain softening model embedded in FLAC3D was established under the assumption that the strength parameters decrease linearly with the equivalent plastic shear strain, without considering the stiffness degradation at the post-peak stage. To address this deficiency, based on Fish programming language, the embedded model in FLAC3D was modified according to the evolution model determined by Eqs. (14) and (15). The mechanical parameters for the numerical simulation are listed in Table 2.

Table 2 Physical parameters of mudstone
Full size table

Fig. 8 shows the numerical simulation model for the mudstone sample. The loading mode is controlled by displacement with an axial velocity of ν=1×10−8 m/s, and the confining pressure was set at 0 MPa, 1 MPa, 3 MPa, 4 MPa, and 5 MPa.

Fig. 8
figure 8

Numerical calculation model of mudstone under tri-axial compression

Full size image

A comparison of the results from the indoor experiment and the numerical simulation is shown in Fig. 9. The simulation results were in good agreement with the experimental results, and the two showed the same change tendency under different confining pressures. The proposed model can accurately describe the residual stage under low confining pressure. However, the simulation results were slightly higher than the experimental results under high confining pressure (3 MPa, 4 MPa, and 5 MPa). On the whole, the peak strength of the simulation results was a little higher than that of the experimental results. This is due to the complexity of damage evolution caused by the development, extension and perforation of micro-cracks in the mudstone sample which cannot be considered in the simulation model. The simulation results showed a small fluctuation near the peak point when σ 3 was set at 5 MPa. This may result from inhomogeneous deformation caused by strain localization.

Fig. 9
figure 9

Comparison of experimental and numerical calculation results for mudstone

Full size image

6 Conclusions

From the results of tri-axial experiments and our evolution model for strength parameters considering stiffness degradation, we draw the following conclusions:

  1. 1.

    The damage threshold of soft mudstone under compression is at the yield point. However, the yield step before the peak point can be treated as an extension of the elastic range due to the relatively short feature and low damage level.

  2. 2.

    Stiffness degradation behavior has a significant influence on the evolution laws of strength parameters. The evolution rule of the friction angle is dominated mainly by the instantaneous stress state and the damage mechanism. The attenuation law of cohesion is related to the plastic behavior in addition to the stress level and damage mechanism.

  3. 3.

    Strength parameters of mudstone show fast attenuation under low confining pressure, and the rate slows down with increasing confining pressure. The friction angle tends towards its initial value under high confining pressure. All the residual strength parameters are enhanced under high confining pressure.

  4. 4.

    Our evolution model considering stiffness degradation in a mudstone sample can accurately demonstrate the attenuation law of strength parameters, thereby providing a theoretical basis for the further study of stability mechanisms of roadways excavated in soft rock strata.