Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grey, D. R.
1974.
Asymptotic behaviour of continuous time, continuous state-space branching processes.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
669.
Grey, D. R.
1974.
Asymptotic behaviour of continuous time, continuous state-space branching processes.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
669.
Bingham, N. H.
and
Doney, R. A.
1975.
Asymptotic properties of super-critical branching processes II: Crump-Mode and Jirina processes.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
66.
Bingham, N. H.
and
Doney, R. A.
1975.
Asymptotic properties of super-critical branching processes II: Crump-Mode and Jirina processes.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
66.
Bingham, N. H.
1975.
Fluctuation theory in continuous time.
Advances in Applied Probability,
Vol. 7,
Issue. 4,
p.
705.
Asmussen, S�ren
and
Hering, Heinrich
1976.
Strong limit theorems for general supercritical branching processes with applications to branching diffusions.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 36,
Issue. 3,
p.
195.
Bingham, N.H.
1976.
Continuous branching processes and spectral positivity.
Stochastic Processes and their Applications,
Vol. 4,
Issue. 3,
p.
217.
Evans, Lawrence S.
1978.
An upper bound for the mean of Yaglom's limit.
Journal of Applied Probability,
Vol. 15,
Issue. 01,
p.
199.
Biggins, J. D.
1979.
Growth rates in the branching random walk.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 48,
Issue. 1,
p.
17.
De Meyer, A.
and
Teugels, J. L.
1980.
On the asymptotic behaviour of the distributions of the busy period and service time in M/G/1.
Journal of Applied Probability,
Vol. 17,
Issue. 03,
p.
802.
De Meyer, Anne-Marie
and
Teugels, J. L.
1980.
On the asymptotic behaviour of the busy-period distribution in M/G/1 queues.
Advances in Applied Probability,
Vol. 12,
Issue. 2,
p.
301.
Biggins, J. D.
and
Shanbhag, D. N.
1981.
Some divisibility problems in branching processes.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 90,
Issue. 2,
p.
321.
Bagley, J. H.
1982.
Asymptotic properties of subcritical Galton-Watson processes.
Journal of Applied Probability,
Vol. 19,
Issue. 3,
p.
510.
Doney, R.A.
1982.
On the exact asymptotic behaviour of the distribution of ladder epochs.
Stochastic Processes and their Applications,
Vol. 12,
Issue. 2,
p.
203.
De Meyer, A.
1982.
On a theorem of bingham and doney.
Journal of Applied Probability,
Vol. 19,
Issue. 1,
p.
217.
Doney, R. A.
1982.
On the existence of the mean ladder height for random walk.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 59,
Issue. 3,
p.
373.
Pakes, Anthony G.
1986.
The Markov branching-castastrophe process.
Stochastic Processes and their Applications,
Vol. 23,
Issue. 1,
p.
1.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Bingham, N. H.
1988.
On the limit of a supercritical branching process.
Journal of Applied Probability,
Vol. 25,
Issue. A,
p.
215.
Griffiths, R. C.
and
Pakes, Anthony G.
1988.
An infinite-alleles version of the simple branching process.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
489.




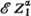 and
and 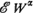 converge or diverge together, and regular variation of the tail of one of
converge or diverge together, and regular variation of the tail of one of 