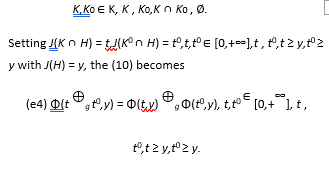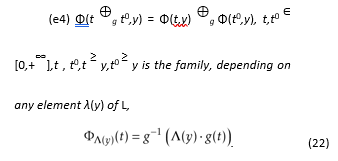1. Introduction

Since 1967 Kampe De Feriet and Forte introduced, by´ axiomatic way, the definition of measures J for general information, where general means that J is defined without probability [1].

Later, in [2], we introduced some particular family of crisp set (N ,F ,I_∞,I₀), in order to study the integration in information theory without probability. We have used them for the definition of measures of general conditional information [3] .

In this paper, we would continue the researches in the setting of Pseudo-Analysis, started in [4], by using pseudo-addition and pseudo-difference. In particular we shall study measures for general conditional information for crisp sets.

The properties of the form of conditional information have translated in a system of functional equations [5], for which we shall give a class of solutions. Moreover, by using the property of Jindependence we obtain another equation: we shall find the general solution through our previous result [6].

The paper is organize in the following way: in Sect.2 we recall some preliminaires; in Sect.3 we give the definition of general information conditioned by a variable event in pseudo-analysis. In Sect.4 we consider the statement of the problem and we traslate the properties of the form of conditional information in a system of functional equations.

We shall distinguish two cases: general case and independent case. In this last case the definition of independence is given by using the pseudo-analysis. We shall show some classes of solutions in Sect. 5. Sect.6 is devoted to the conclusions.

2. Preliminary notations

2.1. Pseudo-operations

We follow the Theory of Pseudo-Analysis introduced by E.Pap and his collegue [7], which consider the definition of pseudo operations. In particular, we shall use the pseudo-addition and the pseudo-difference: for knownledge about these pseudo-operations, we refer to [8].

Definition 2.1 The pseudo-addition ⊕ is a binary

function

⊕ : [0,M] 2 −→ [0,M], M ∈ (0,+∞],

which is commutative, associative, strictly increasing with respect ≤, with 0 as neutral element.

We shall consider only particular operation expressed by a function g, called generator function in the following way:

2.2 Measures of general information in classical analysis

Following [1], let X be an abstract space and A an algebra of all subsets of X, such that (X,A) is a measurable space.

Definition 2.3 Measure of the general information is a mapping

is not an filter [9] because it is not stable with respect to the intersection between fuzzy sets.

Given the family H = A − I_+∞ we recall from [3],

Definition 2.5 The measure of general conditional information of any set A ∈ A conditioned by a fixed H ∈ H, (J(A|H)) is a mapping

3 Pseudo-analysis: measures of general conditional information

In [4], for the first time, we have introduced the definition of J− independence property in the setting of pseudo-analysis, and we have used it to find the information of the union of two sets A,A⁰ ∈ A : J(A ∪ A⁰). From now on we consider a pseudo-addition ⊕_g generated by a function g as in (1).

Definition 3.1 Given a subfamily K ⊂ A, and a pseudo-addition ⊕_g, two sets K,K⁰ ∈ K , are called Jindependent in pseudo-analysis if the couple (K,K⁰) satisfies the following:

4. Statment of the problem: the function Φ

In this paragraph, fixed an information J, we would look for the measure of general conditional information of any set A ∈ A conditioned by a fixed H ∈ H,

4.1      General case

The conditions (2.5.1)-(2.5.3) become:

4.2      Independent case

In this paragraph, we shall consider J− independent sets in pseudo-analysis.

We suppose that there exist two sets K,K0 ∈ K,K ,K 0, K ∩ K 0 , ∅, which are J independent in pseudoanalysis in the sense of (6). From (7), and taking into account (8), it is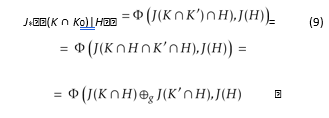

5         Solutions of the problem

Now, we are giving some solutions of the problem, distinguishing two previous cases.

5.1      General case

Proposition 5.1 A class of continuous solutions of the system (e1) − (e3) is

where ρ : [0,+∞] → [0,+∞] is any bijective , continuous, strictly increasing function, with ρ(0) = 0, ρ(+∞) = +∞ and  is defined in (2).

Proof. The condition (e1) is satisfied as the composition of two increasing functions ρ and g. The conditions (e2) and (e3) are verified by the values g(0) = ρ(0) = 0 and ρ(+∞) = g(+∞) = +∞. Moreover ρ is continuous as the generator function g.

Proposition 5.2 Another class of continuous solutions of the system (e1) − (e3) is

where µ is the product of the generator function g of the operation        _g given by (2) and m is any function as in

(12).

Proof. Let m be a particular function solution of the system (e1) − (e3) as in Prop.[5.1], which defines a pseudo-addition ⊕_m. From (2) and (10), it is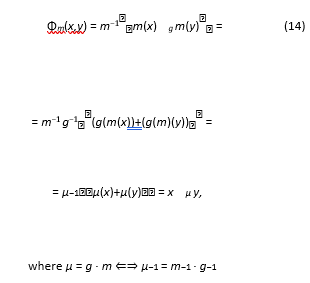

where µ = g · m ⇐⇒ µ−1 = m−1· g−1

By the properties of g and m the solutions are continuous.

Any function ρ in Prop.[5.1], in general, doesn’t define a pseudo-addition of the kind ⊕_g as in (1) because it is not commutative, neither associative. For this reason the Prop.[5.2] is not a consequence of

Prop.[5.1].

Vivona et al. / Advances in Science, Technology and Engineering Systems Journal Vol. 2, No. 2, 36-40 (2017)

5.2      Independent case

Now, we rewrite the equation (e4):

on suitable hypothesys on the function F, when ⊕ is any pseudo-addition not necessary expressed by a generator function g. The equation (17) has been solved by Benvenuti and the authors in [6] in many general cases.

In particular, when this pseudo-addition is generated by function g, we found all continuous solutions. Here, we neglect trivial solutions and we consider only the most meanigfull solution. We recall the result from [6]:

Theorem 5.3 The solution of the general Cauchy equation

generator function of the pseudo-addition

(2).

Now, we can go back to our original problem concerning the J− independence property in pseudoanalysis and we are ready to give the main theorem.

Let L be any family of continuous function Λ : (0,+∞) → (0,+∞) :

L = {Λ : (0,+∞) → (0,+∞),continuous}.             (21) Theorem

5.4 The class of continuous solutions of the equation

Proof. Now, fixed any function Λ(y) ∈ L, we are verifying that (22) is solution of (e4):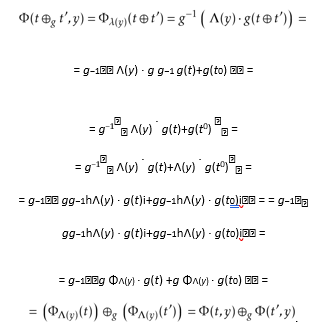

It is easy to see that any function (22) is continuous.

Proposition 5.5 The function Φ_Λ(y)(t) given by (22) is strictly increasing with respect to the variable t.

Proof. The monotonicity of the function Φ_Λ(y)(t) doesn’t depend on the variable y; moreover Λ(y) is positive. Then,

As conseguence of Theorem [5.4] and of Proposition [5.5], we get the following

Theorem 5.6 The only solution of the equations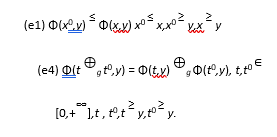

is the family, depending on any element of L, given by

(21),

It is easy to see that the conditions (e2) and (e3) are not compatible with the independent property.

6. Conclusion

In this paper, given a measure of general information J, we have defined the measure of general conditional information J^∗(A|H) of any set A ∈ A conditioned to H ∈ H. Moreover, we have considered J^∗(A|H) depending only on J(A ∩ H) and J(H) through a function Φ. The properties of this J^∗(A|H) are translated in a system of functional equations. In order to look for solutions of the system, we distinguish two cases: the first concerning monotonicity and particular values of J^∗(A|H), system (e1)-(e3), the second one related to monotonicity and independence property, equations (e1) and (e4).

I-General case: system (e1)-(e3) Some classes of the measure of general conditional information are: from (12)

depending on a class of functions  L, where  L is defined in (21).

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This research is in the framework of GNFM (Gruppo Nazionale per la Fisica Matematica) del MIUR (Ministero Italiano per l’Universita e la´ Ricerca), ITALY.

1. J.Kampe De Feriet, B.Forte, Information et Prob-abilite applications” Compt.Rand.Ac.Sc.Paris, 265, 110-114, 142-146, 350-353, 1967.
2. D.Vivona, Information Theory and Fuzzy Inte-grals: along the way paved by Pietro Benvenuti, 10th International Conference on Information Processing and Management of Uncertainty in Knowledge-based System (IPMU), Perugia Italy, 2004.
3. D.Vivona – M.Divari, On a conditional informa-tion for fuzzy sets, International Summer School on Aggregation Operators and their applica-tions (AGOP), Lugano Switzerland, 2005.
4. D.Vivona – M.Divari, Pseudo-Analysis: some measures of general information, IEEE 14th In-ternational Symposium on Intelligent Systems and Informatics (SISY), Subotica Serbia, 2016.
5. J. Aczel, Lectures on functional equations and their applications, New Jork, Academic Press, 1966.
6. P.Benvenuti – R.Mesiar – D.Vivona, The cauchy equation on I-semigroup, Aequ.Math. 63, 2002.
7. E. Pap, Null-additive Set Functions Dordrecht. Kluver Academic Publishers, 1995.
8. P.Benvenuti – R.Mesiar – D.Vivona, Mono-tone set-functions-based integrals, Handbook in Measure Theory, Elsevier Ed. 2002.
9. K.Yosida, Functional analysis, Springer, 1995.
10. D.Vivona – M.Divari, An Independence prop-erty for General Information, Natural Sciences 8 2016, dx.doi.org/10.4236/ns.2016.82008.

(Click to view)

(Click to view)