A Review on Time Series Aggregation Methods for Energy System Models
Abstract
:1. Introduction
1.1. Drivers of Model Complexity
1.2. Motivation and Scope of the Review
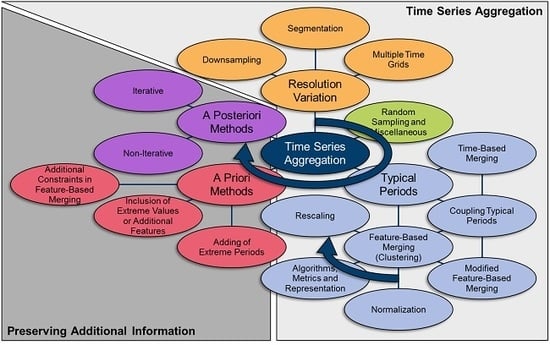
2. Methodology and Structure of the Review
2.1. Methodology of the Literature Research
2.2. Structure of the Review
3. Time Series Aggregation
3.1. Resolution Variation
3.1.1. Downsampling
3.1.2. Segmentation
3.1.3. Multiple Time Grids
3.2. Typical Periods
3.2.1. Time-Based Merging
3.2.1.1. Averaging
3.2.1.2. Time Slices
3.2.1.3. Time Slices/Averaging + Downsampling/Segmentation
3.2.2. Feature-Based Merging
- A normalization (and sometimes a dimensionality reduction).
- A distance metric.
- A clustering algorithm.
- A method to choose representatives [59].
- A rescaling step in the case of non-centroid based clustering algorithms.
3.2.2.1. Preprocessing and Normalization
3.2.2.2. Algorithms, Distance Metrics, Representation
3.2.2.3. Rescaling
3.2.3. Modified Feature-Based Merging
3.2.4. Linking Typical Periods
3.3. Random Sampling
3.3.1. Unsupervised
3.3.2. Supervised
3.4. Miscellaneous Methods
3.5. Overview and Trends in Aggregation
4. Preserving Additional Information
- Values of the original time series which could be especially important for the ESM are usually not preserved.
- A reliable estimation of the deviation of the optimization result based on aggregated time series from the one based on full time series can usually not be given.
4.1. A Priori Methods
4.1.1. Adding Extreme Periods
4.1.2. Inclusion of Extreme Values or Additional Features
4.1.3. Additional Constraints in Feature-Based Merging
4.2. A Posteriori Methods
4.2.1. Non-Iterative
4.2.2. Iterative
- Separating complicating binary variables from the vast majority of continuous variables.
- Separating the design problem from the operational problem.
- Obtaining feasible but suboptimal solutions instead of optimal but infeasible solutions for the fully resolved input data.
- Deriving implications for a meaningful TSA from the system itself instead of the input data only.
- Determining a more robust energy system by exposing the once optimized energy systems to different input data scenarios.
4.3. Overview and Trends in the Integration of Additional Information
5. Conclusions
- The question of the most important statistical features of the time series to be kept, i.e., whether the clustering of statistical features in a lower dimensional space is superior to the traditional TSA methods.
- A way to measure the accuracy of different aggregation methods a priori by defining bounds that are also valid for the computationally intractable problem.
- Enhancing the convergence rate of iterative methods in order to compete with the branch-and-bound or decomposition methods of commercial solvers
- Developing an approach that is capable of identifying the most critical situations in input time series in a non-empirical manner. This could lead to robust optimizations not based on MonteCarlo-like approaches.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| DTW | Dynamic Time Warping |
| ESM | Energy System Model |
| GEP | Generation Expansion Planning |
| MILP | Mixed Integer Linear Program |
| RES | Renewable Energy Sources |
| TR | Temporal Resolution |
| TD | Typical Day |
| TTS | Typical Time Step |
| TS | Time Slice |
| TSA | Time Series Aggregation |
| UC | Unit Commitment |
Appendix A
| Year | Author | ESM for Case Study, (Framework) | Normalization | Distance Metric | Clustering/Grouping | Representative | Extreme Periods | Linking Periods | Duration Curve |
|---|---|---|---|---|---|---|---|---|---|
| 1999 | Balachandra et al. [53] | None (just approach) | No | No | Multiple discriminant analysis | Mean | No | Yes | No |
| 2002 | Yokoyama et al. [66] | Building or district model, no storage technologies, but multiple commodities | No | No | Season-based (summer, mid-season, winter) with 4-, 2-, or 1- h resolution | (probably) Mean | No | No | No |
| 2007 | Lee et al. [183] | UC problem for 48 unit power system (not further specified) | No | No | No | No | No | Yes | No |
| 2007 | Swider et al. [122] | Single-node model for electricity production in Germany with wind and pumped hydro storage | No | No | Every two months, one weekday and one weekend day with 2-h resolution | (probably) Mean | No | No | No |
| 2008 | Marton et al. [98] | None (just approach) | No | Integral of absolute error (L1 norm) | Clustering by comparing each new day to clusters of preceding days | Mean | Yes, if outlier surpass a certain threshold of the IAE and the following day is close to the preceding cluster | Yes | No, although curve was called the duration curve |
| 2008 | Mavrotas et al. [54] | Building model for a hospital, no storage technologies, but multiple commodities | No | No | Monthly average | Mean | No | No | No |
| 2008 | Mavrotas et al. [54] | Building model for a hospital, no storage technologies, but multiple commodities | No/not mentioned | No/not mentioned | Seasonal rescaled average further segmented | Rescaled mean | Peak demand value of each cluster is kept for each attribute | No | No |
| 2009 | Alzate et al. [195] | Customer or unit partitioning/none (just approach) | Z-normalization | No (Hamming distance for out-of-sample extension) | Spectral clustering | None (just grouped) | No | No | No |
| 2009 | Casisi et al. [114] | District model, no storage technologies, but multiple commodities | No | No | Season-based (3 seasons for energy demand and 24 for sold energy to the grid) | (probably) Mean | No | No | No |
| 2009 | Lozano et al. [111] | Building model for a hospital, no storage technologies, but multiple commodities | No | No | Monthly average with distinction between weekday and weekend | (probably) Mean | No | No | No |
| 2010 | Lozano et al. [99] | District model, thermal storage units, multiple commodities | No | No | Monthly average | (probably) Mean | No | No | No |
| 2010 | Nicolosi et al. [104] | Single-node electricity dispatch model for Texas (ERCOT), no storage, technologies mentioned, (THEA) | No | No | Full resolution, 4 seasons, Wednesday, Saturday and Sunday with hourly resolution, 16 time slices | Means | No | No | No |
| 2011 | Domínguez-Muñoz et al. [55] | None (just approach) | Yes, but not mentioned which | Euclidean | k-medoids | Medoids | Peak heating and peak cooling day | No | No |
| 2011 | Haydt et al. [105] | Island electricity model for Flores (Azores), no explicitly modeled storage technologies (only via availability), (TIMES, LEAP, EnergyPlan) | No | No | LEAP: 9 time slices from the duration curve TIMES: 4 seasons, Wednesday, Saturday, and Sunday with hourly resolution EnergyPLAN: full hourly resolution | Means | No | Yes | LEAP: Yes TIMES: No |
| 2011 | Ortiga et al. [179] | Building model, thermal storage units, multiple commodities | No/not mentioned | No/not mentioned | Graphical method | Existing days | Peak heating and peak cooling day | No | Yes |
| 2011 | Pina et al. [124] | Island electricity model for São Miguel (Azores), no explicitly modeled storage technologies (only via availability), no storage technologies, (TIMES) | No | No | 4 seasons, weekday, Saturday and Sunday with hourly resolution | (probably) Mean | No | Yes | No |
| 2011 | Weber et al. [112] | Multi-node district model, daily heat and electricity storages, multiple commodities | No | No | 3 seasons further segmented into 6 irregular periods | (probably) Mean | No | No | No |
| 2012 | Buoro et al. [89] | Building model, thermal storage units, multiple commodities | No | No | Monthly average, typical weeks with 168 h | (probably) Mean | No | No | No |
| 2012 | Devogelaer et al. [125] | Multi-node model for Belgium, multiple storage technologies, multiple commodities, (JRC-EU-TIMES) | No | No | 26 2-week periods with three daily levels | (probably) Mean | Peak demand slice | Yes | No |
| 2012 | Mehleri et al. [129] | District model, no storage technologies, multiple commodities | No | No | 3 seasons further segmented into 6 irregular periods | (probably) Mean | No | No | No |
| 2012 | Van der Weijde et al. [180] | Multi-node electricity model for Great Britain, no explicitly modeled storage technologies (only as source/sink) | No | No | N hourly samples | Existing hours | No | No | No |
| 2012 | Welsch et al. [106] | Single-node electricity model for a town, battery storages, demand shifting, (OSeMOSYS) | No | No | In Proposal: 4 seasons, work days and weekends, 3 daily intervals. In example: Just one day in hourly resolution | (probably) Mean | No | Yes | No |
| 2013 | De Sisternes et al. [93] | Single-node electricity model, no storage technologies, but minimum up- and down-times | Min-max normalization for NLDC | Euclidean | Exhaustive search or heuristic | Existing weeks | Including peak week or peak day | No | Yes |
| 2013 | Kannan et al. [126] | Single-node electricity model for Switzerland and pumped hydro storage, (TIMES) | No | No | Season-based (four seasons and to diurnal time slices), or weekdays, Saturdays, Sundays in hourly resolution | Average | No | Yes | No |
| 2013 | Mehleri et al. [130] | District model, thermal storage units, multiple commodities | No | No | 3 seasons with hourly resolution | (probably) Mean | No | No | No |
| 2013 | Pina et al. [115] | Electricity model for Portugal, storage technologies considered, but modeling not explained, number of regions not mentioned, (TIMES and EnergyPLAN) | No | None | One weekday, one Saturday and one Sunday, 4 seasons | Not mentioned | No | No | No |
| 2013 | Simões et al. [127] | Multi-node model for Europe, multiple storage technologies, multiple commodities, (TIMES) | No | No | Season-based (four seasons, day, night and peak time slice) | Average | Average peak demand during each season | Yes | No |
| 2013 | Spiecker et al. [116] | Multi-node electricity model for Europe, hydro storage units, cogeneration units on regional scale | No/not mentioned | None | One weekday and one weekend day for every two months with 2 h resolution | Not mentioned | Yes, with stochastic approach | Yes | No |
| 2013 | Voll et al. [103] | District model, no storage technologies, multiple commodities | No | No | Monthly average | Mean | Two more time steps for summer and winter peak loads | No | No |
| 2014 | Adhau et al. [153] | Stochastic single-node electricity model, no storage technologies | No/not mentioned | Euclidean | k-means | Centroids | No | No | No |
| 2014 | Benítez et al. [196] | Customer or unit partitioning/none (just approach) | No/not mentioned (only one attribute) | Euclidean | Dynamic k-means | Centroids | No | Yes (yearly trajectory) | No |
| 2014 | Deane et al. [64] | UC of the Irish electricity system, pumped hydro storage, (PLEXOS) | No | No | Downsampling (5, 15, 30 and 60 min) | Average | No | Yes | No |
| 2014 | Fazlollahi et al. [138] | District heating model, no storage technologies | Min-max normalization | Euclidean | k-means | Centroids | Attribute peaks | No | No |
| 2014 | Fazlollahi et al. [69] | Two single-node district models with fixed capacities, no storage technologies, multiple commodities, UC (minimizing operating costs) | Min-max normalization | Euclidean | k-means and segmentation | Centroids | Attribute peaks | No | No |
| 2014 | Green et al. [154] | Electric dispatch model for UK, pumped hydro storage simulated, number of regions not mentioned | No (just two attributes of same scale clustered) | Euclidean | k-means | Centroids | Dominant ramp integration | No | No |
| 2014 | Poncelet et al. [36] | Island electricity model for Belgium, no storage technologies or transmissions, re-evaluation with UC model, (TIMES) | No | No | Season-based (four seasons, night, day and peak slice) | (probably) Mean | By choosing peak slice | No | No |
| 2014 | Stadler et al. [113] | Building model, multiple storage technologies, multiple commodities (DER-CAM) | No | No | (seven typical days or one typical weekday, one typical weekend day and one peak day) | (probably) Mean | Peak demand day in case of typical weekday and typical weekend day | No | No |
| 2014 | Wakui et al. [110] | Building model, thermal storage units, multiple commodities | No | No | Season-based | (probably) Mean | Peak summer day and peak winter day | No | No |
| 2014 | Wogrin et al. [85] | Single-node electricity model, no storage technologies | No (attributes of the same unit) | Euclidean | k-means, hourly, 6 system states | Centroids | No | No | No |
| 2014 | Xiao et al. [186] | Island electricity model for, no storage technologies | No | No | No | No | No | Yes | No |
| 2015 | Agapoff et al. [63] | Multi-node electricity model for GEP, no storage technologies | No/not mentioned | Euclidean | k-means, typical hours (snapshots) | Medoids | Included as clustered features (min, max, std., local difference and avg.) | No | No |
| 2015 | Brodrick et al. [155] | Single-node model of a coal-plant with alternative natural gas and solar thermal heat sources and carbon capture and storage, CO2 solvent storage unit, multiple commodities | Normalization by dividing by the average | Euclidean | k-means | Centroids | No | No | No |
| 2015 | Bungener et al. [70] | UC of a chemical cluster, multiple commodities | Normalized by average values and multiplied by weight | None, but variance indicator and zero flowrate indicator | Evolutionary mechanisms (segmentation) | Means | No | Yes (adjacent time steps are merged) | No |
| 2015 | Deml et al. [71] | Single-node electric dispatch model, pumped hydro storage | No | No | Progressive downsampling | Means | No | Yes | No |
| 2015 | Fitiwi et al. [142] | IEEE 24-bus Reliability Test System [197], multi-node electricity model, no storage technologies | Normalized by maximum line length and base load | Euclidean | k-means, typical hours (snapshots) | Medoids closest to the clusters’ centroids | No | No | No |
| 2015 | Harb et al. [101] | Building model and district model, thermal storage units, multiple commodities | No | No | Monthly average, also 15 min. and hourly resolution | Mean | No | No | No |
| 2015 | Harb et al. [90] | District model, thermal and battery storage units, multiple commodities | No | No | Cluster by sums of weeks (sensitivity analysis also for different day numbers), typical weeks | Means | No | No | No |
| 2015 | Marquant et al. [149] | District heating model, no storage technologies, multiple commodities | No/not mentioned | Euclidean | k-medoids | Medoids | Peak electricity and peak heating days | No | Yes |
| 2015 | Merkel et al. [91] | District model, thermal storage units, multiple commodities | No | No | Season based (three weeks from spring/autumn, summer and winter), 15 min. resolution | (probably) Existing weeks | No | No | No |
| 2015 | Munoz et al. [181] | IEEE Reliability Test System [188], multi-node electricity model, no storage technologies | No/not mentioned | Euclidean | Daily moment-matching, k-means for hours, typical hours (snapshots) | Centroids | Top 10 peak load hours included | No | No |
| 2015 | Poncelet et al. [177] | None (just approach) | No/not mentioned | L1-Norm | Using so-called “bins” | Existing days | No | No | Yes |
| 2015 | Samsatli et al. [16] | Multi-node island model, multiple hydrogen storage technologies, multiple commodities | No | No | Season-based (four seasons, weekdays and weekend days) | (probably) Mean | No | Yes | No |
| 2015 | Schiefelbein et al. [163] | District model, thermal storage units, multiple commodities | No/not mentioned | Euclidean | k-medoids | Medoids | No | No | |
| 2015 | Wakui et al. [109] | Building model, thermal and battery storage units, multiple commodities | No | No | Season based | (probably) Mean | Peak summer day and peak winter day | No | No |
| 2015 | Wouters et al. [117] | District model, heat, cold and battery storage technologies, multiple commodities | No | No | Season-based (spring/autumn, summer and winter) | (probably) Mean | Sensitivity analysis by adding variability to PV input data | No | No |
| 2015 | Yang et al. [118] | District model, heat and cold storage technologies, multiple commodities | No | No | Season-based (spring/autumn, summer and winter), 2 h resolution | (probably) Mean | No | No | No |
| 2015 | Yokoyama et al. [67] | Building model for a hotel, no storage technologies, but multiple commodities | No | No | Season-based (summer, mid-season, winter) with 8, 4, or 2 h resolution and for commercial solver 1 h | (probably) Mean | No | No | No |
| 2016 | Ameri et al. [119] | District model no storage technologies, multiple commodities | No | No | Season-based (summer and winter) | (probably) Mean | No | No | No |
| 2016 | Beck et al. [65] | Electric building model, battery storage | No | No | Single day downsampled (10, 30, 60, 300, 900, 3600 s), analyzed single days | Mean | No | Yes | No |
| 2016 | Bracco et al. [120] | District model, thermal and battery storage technologies, multiple commodities, (DESOD) | No/not mentioned | No | Season-based (summer, winter, mid-season) | (probably) Mean | No | No, initial conditions at each day, e.g., | No |
| 2016 | De Sisternes et al. [92] | Single-node electricity model, battery storage and minimum up- and down-times | Min-max normalization for NLDC | Euclidean | Exhaustive search or heuristic (refers to [93], but with additional cycled power error), typical weeks | Existing weeks | Including peak week or peak day | No | Yes |
| 2016 | Frew et al. [182] | Multi-node electric model of the US, pumped hydro, thermal and battery storage technologies, (POWER) | Yes, but not mentioned is which, but averaged across all potential developable sites | None | Random days | Existing days, weights calculated with least squares method | Extreme days containing the peak value for each of the eight attributes | No (net storage values of each day must be zero or SOC at start of each day equals that at the end) | Yes |
| 2016 | Haikarainen et al. [198] | Customer or unit partitioning/district model, thermal storage units, multiple commodities | No | Euclidean | k-means | Means | No | No | No |
| 2016 | Kools et al. [102] | District electricity model, battery storage units, heat demand driven CHP units considered | No | No | Averaging of eight consecutive weeks in each season to one typical day | Mean | Normal distributions added for 1 min, 15 min and 1 h resolution (stochastic impact) | Control policy for the storage (not across days) | No |
| 2016 | Lin et al. [156] | Multiple building models, thermal and battery storage units, multiple commodities | No/not mentioned (attributes of the same unit) | Euclidean | k-means | Existing day which is closest to the centroid | No | No (periodic SOC) | No |
| 2016 | Lythcke-Jørgensen et al. [88] | CHP-plant model, no storage technologies, multiple commodities | Heat demand normed by maximum value | No/not mentioned | So-called “CHOP” aggregation (graphical method) for five years of hourly data | Means | No | No | No |
| 2016 | Merrick et al. [40] | Single-node electricity model, no storage technologies | No | None | Monthly median and peak electricity demand day with 4 h resolution and only one averaged period | Medoids | Peak electricity demand days | No | No |
| 2016 | Nahmmacher et al. [143] | Multi-node electricity model LIMES-EU [199] with intraday storage technologies, (LIMES-EU) | Demand: region-specific divided by maximum value VRE: divided by maximum value across all regions | Euclidean | hierarchical | Medoids | No | No | No |
| 2016 | Oluleye et al. [123] | Single-node district model, thermal storage units, multiple commodities | None | None | One weekday and one weekend day for winter, summer and transition with 7 (6) time bands (slices) | Not mentioned | No | No | No |
| 2016 | Patteeuw et al. [94] | Building heating model of nine buildings, thermal storage units, multiple commodities | No/not mentioned, Demand: region-specific divided by maximum value | L1-Norm | Using so-called “bins”, heuristic, hierarchical clustering according to Nahmmacher et al. [143] for the years of 2013–2016 | Existing weeks (6) | Coldest week and week with highest e-demand (same week) | No | Yes |
| 2016 | Ploussard et al. [87] | IEEE 24-bus Reliability Test System [197], multi-node electricity model, no storage technologies | No/not mentioned | Euclidean | k-means, typical hours (snapshots) | Existing snapshot closest to the centroids | No | No | No |
| 2016 | Poncelet et al. [128] | Island electricity model for Belgium, no storage technologies or transmissions, re-evaluation with UC model, (TIMES) | No | None | For each of the four seasons one night, day and peak electricity time slice | Mean | Peak electricity time slice | No | No |
| 2016 | Poncelet et al. [144] | Single-node electricity model based on [200], no storage technologies, (LUSYM) | No/not mentioned, Demand: region-specific divided by maximum value | L1-Norm, Euclidean | Using so-called “bins”, heuristic, hierarchical clustering according to Nahmmacher et al. [143] | Existing days, medoids | No, for heuristics days with highest and lowest value for e-demand and highest and lowest average for wind and PV | No | Yes |
| 2016 | Samsatli et al. [17] | Multi-node hydrogen-electricity model for Great Britain, multiple hydrogen storage units, multiple commodities | No | No | Season-based (four seasons, work days and weekend days) | (Probably) Mean | No | Yes | No |
| 2016 | Schütz et al. [139] | Building model, thermal and battery storage units, multiple commodities | Min-max normalization | Euclidean | k-means k-medians k-medoids k-centers | Centroids Medians Medoids Centers | No | No | No |
| 2016 | Stenzel et al. [38] | UC of building electricity model with battery storage | No | None | downsampling | Means | No | Yes | No |
| 2016 | Wakui et al. [108] | Building model, thermal and battery storage units, multiple commodities | No | No | Season based | (probably) Mean | Peak summer day and peak winter day | No | No |
| 2016 | Wogrin et al. [83] | Single-node electricity model, pumped hydro and battery storage | No/not mentioned | Euclidean | k-means (98 system states (typical hours)) | Centroids | No, but the first and last hour of the time horizon were manually added | Yes | No |
| 2017 | Bahl et al. [157] | District model from Voll et al. [103], no storage technologies, multiple commodities | No/not mentioned (attributes of same scale clustered) | (probably) Euclidean | k-means, typical hours (snapshots) | Centroids | Feasibility time steps (peak values) and operation optimization for full time series | No | No |
| 2017 | Brodrick et al. [146] | UC of an integrated solar combined cycle, no storage technologies, multiple commodities | Z-normalization | Euclidean | k-means | Centroids | No | No | No |
| 2017 | Härtel et al. [86] | Multi-node transmission expansion planning model, no storage technologies | Either normed by highest value per market or highest value across all markets | Euclidean | k-means, k-medoids, hierarchical, systematic sampling, moment-matching, typical hours (snapshots) | Centroids, medoids, sample points | Heurisitc defining new cluster centers if 95% of a cluster’s data points are below or above a 6 h moving average, with the lowest or highest chosen as the new cluster center | No | No |
| 2017 | Heuberger et al. [158] | Single-node electricity model with carbon capture and storage and grid-level storage | Yes, but not mentioned which | Euclidean | k-means | Means | Day with annual electricity peak demand | No | No |
| 2017 | Marquant et al. [150] | District heating model, thermal and battery storage units, multiple commodities | No/not mentioned | Euclidean | k-medoids | Medoids | Peak electricity and peak heating days | No | Yes |
| 2017 | Moradi et al. [121] | Single-node model of an energy hub, thermal and battery storage, multiple commodities | No | No | Season-based (one work day and one weekend day per spring, summer, autumn and winter) | (probably) Mean | No | No | No |
| 2017 | Pfenninger et al. [37] | Multi-node electricity model for Great Britain, pumped hydro and battery storage units | Normalized by the maximum value across all time steps and model zones | Euclidean | k-means, hierarchical, downsampling, heuristics | Centroids, medoids | Min/max solar and wind days, wind and PV weeks and wind-demand weeks | No | No |
| 2017 | Renaldi et al. [61] | Single-node district heating system, long- and short-term thermal storage units, multiple commodities | No | None | Multiple time grids for different storage technologies | Downsampled 3 h steps for long-term storage | No | Yes | No |
| 2017 | Timmerman et al. [107] | Two business park models (one based on the model of Voll et al. [103]), thermal and electrical storage units, multiple commodities, (Syn-E-Sys) | No | No | Season and weekday-based (4 × 2 × 4 6 h intervals) | (probably) Mean | No | Yes | No |
| 2017 | Schütz et al. [100] | Building model, thermal and battery storage units, multiple commodities | No | No | Monthly average (one typical day per month and weighted) | (probably) Mean | No | No | No |
| 2017 | Sun et al. [136] | Customer or unit partitioning/none (just approach) | Time steps wise (in period) average s divided by maximum value of each customer | Likelihood-function | Vine-copula mixture model | None | No | No | No |
| 2017 | Teichgräber et al. [147] | Oxyfuel natural gas plant, liquid oxygen storage, multiple commodities | Z-Normalization | Euclidean | k-means | Centroids | No | No | No |
| 2017 | vom Stein et al. [79] | Multi-node electricity dispatch model for Europe, pumped hydro storage | No | L1-Norm | Clustering of consecutive time steps with objective to minimize gradients within clusters | Mean | No | Yes (clustering of consecutive time steps) | No |
| 2017 | Yang et al. [201] | Customer or unit partitioning/none (just approach) | Z-normalization | Shape-based distance | k-shape | None | No | No | No |
| 2017 | Zhu et al. [164] (refers to [55]) | Building model for an airport in China optimizing economics or CO2 emissions, no storage technologies, but start-up and shut-down costs | Yes, but not mentioned which | Euclidean | k-medoids (only three season-specific typical days) | Medoids | No | No | No |
| 2018 | Almaimouni et al. [137] | Single-node GEP for electricity, validated with rolling horizon UC, no storage technologies | Normalize by with m as number of days, principal components | Euclidean | k-means | Centroids | No | No | Only as error estimator |
| 2018 | Bahl et al. [192] | District model from Voll et al. [103] and a single-node pump system, no storage technologies, multiple commodities | No/not mentioned (attributes of same scale clustered) | Euclidean | k-means, typical hours (snapshots) | Undersestimators from minimum values of each cluster | Feasibility time steps (peak values) and operation optimization for full time series | No | No |
| 2018 | Bahl et al. [74] | District model from Voll et al. [103] with additional heat and cold storage units, multiple commodities | Yes, but not mentioned which | Euclidean | k-medoids (daily clustering and segmentation) | Medoids further segmented | Feasibility time steps (peak values) and operation optimization for full time series | No | No |
| 2018 | Brodrick et al. [97] refers to [146] | UC of an integrated solar combined cycle, no storage technologies, multiple commodities | Z-normalization | Euclidean | k-means (6 representative days) further reduced to three extreme hours | Centroids | Three extreme hours | No | No |
| 2018 | Gabrielli et al. [15] | Single-node district model, thermal, battery and hydrogen storage, multiple commodities | No/not mentioned | Not mentioned (probably Euclidean/default for Matlab k-means) | k-means | Centroids | Maximum and minimum values of the demand profiles | Yes | No |
| 2018 | Kotzur et al. [57] | Three single-node models (CHP system, residential building, island system), thermal, battery and hydrogen storage, multiple commodities | Min-max normalization | Euclidean | k-means, averaging, k-medoids, hierarchical, typical days and typical weeks | Centroids medoids | Peak periods heat and electricity demand, minimum PV feed-in | No | No |
| 2018 | Kotzur et al. [14] | Three single-node models (CHP system, residential building, island system), thermal, battery and hydrogen storage, multiple commodities | Min-max normalization | Euclidean | Exact k-medoids | Medoids | No | Yes | No |
| 2018 | Lara et al. [24] | Multi-node electricity model for Texas, multiple storage units (e.g., lithium-ion, lead-acid, and flow batteries) | Mentioned, but not which one | Euclidean | k-means for the years of 2004–2010 | Centroids | No | No, 50% SOC heuristic | No |
| 2018 | Liu et al. [148] | Multi-node electricity model for Texas (greenfield GEP), storage units and ramping constraints considered | Z-Normalization | DTW distance, Euclidean as benchmark | (k-means initially), hierarchical, k-means as benchmark | Medoids, centroids for k-means-benchmark | No | No | No |
| 2018 | Mallapragada et al. [39] (2004–2010) | Electricity GEP model for Texas, no storage or transmission units, ramping in production cost simulation considered | Min-max normalization between 0 and 2 | Euclidean and L1-Norm (as benchmark) | 4 seasons and 4 daily segments vs. k-means | Medoids | No | No, refers to [24], 50% heuristic | No |
| 2018 | Neniškis et al. [51] | Electricity and district heat model of Lithuania, pumped hydro storage, multiple commodities, (MESSAGE) | No | None | Workday and weekend day either for four seasons or for twelve months | Mean | No (but synthesized wind time series) | No | No |
| 2018 | Pineda et al. [72] | Multi-node electricity model of Europe, intraday, interday storage and ramping constraints considered | Mentioned, but not which one | Euclidean | Hierarchical | Medoids | No | Yes, by clustering adjacent periods | No |
| 2018 | Schütz et al. [58] | Building model, thermal and battery storage units, multiple commodities | Min-max normalization | Euclidean | k-means k-medians k-medoids k-centers | Centroids medians medoids centers | No | No | No |
| 2018 | Stadler et al. [165] | Building model, thermal and battery storage units, multiple commodities | No/not mentioned | (probably) Euclidean | k-medoids | Medoids | No | No | No |
| 2018 | Teichgräber et al. [159] | Two minimal UC problems: An electricity storage model and a gas turbine dispatch model | Element-wise Z-Normalization | Euclidean, Dynamic Time Warping, Shape-based Distance | k-means k-medoids Barycenter Averaging k-shape hierarchical | Centroid, medoids | No | No | No |
| 2018 | Tejada-Arango et al. [19] | UC of the Spanish electricity system, battery and pumped hydro storage | Yes, but not mentioned what kind of normalization | (probably) Euclidean | k-medoids for RP, k-means for SS | Medoids, centroids | No | Yes | No |
| 2018 | Tejada-Arango et al. [84] | UC of the IEEE 14 bus electricity model, battery and pumped hydro storage | No/not mentioned (attributes of same scale clustered) | Euclidean | k-means (for typical hours) | Centroids | No | No | No |
| 2018 | Tupper et al. [167] | UC of the IEEE 30 bus electricity model with wind generation, no storage technologies | No/not mentioned | Euclidean, band distance | k-medoids | Medoids | No | No | No |
| 2018 | Van der Heijde et al. [95] | Single-node district heating model, thermal storage | No/not mentioned | L1-Norm | Using so-called “bins” and four seasons | Existing weeks | No, but each season needs to contain at least one typical week | Yes | Yes |
| 2018 | Voulis et al. [145] | Customer or unit partitioning/none (just approach) | Normalization by maximum e-demand | Euclidean | k-means (spatio-temporal differentiation between workdays, weekends, neighborhoods, districts and municipalities) | Centroids | No | No | No |
| 2018 | Welder et al. [18] | Multi-node model for power-to- hydrogen in Germany, hydrogen storage technologies, multiple commodities | Min-max normalization | Euclidean | hierarchical | Medoids | No | Yes | Yes |
| 2019 | Baumgärtner et al. [78] | District model from Voll et al. [103] with additional heat and cold storage units and a single-node pump system, multiple commodities | No/not mentioned | Euclidean | k-medoids | Segmented under- and overestimators | Feasibility time steps (peak values) and operation optimization for full time series | No | No |
| 2019 | Baumgärtner et al. [77] | Single-node model for industrial site based on Baumgärtner et al. [202] with heat, cold and battery storage, Multi-node model for Germany with battery and hydrogen storage, multiple commodities | No/not mentioned | Euclidean | k-means | Centroids, segmented under- and overestimators | Feasibility time steps (peak values) and operation optimization for full time series | Yes | No |
| 2019 | Gabrielli et al. [160] | Single-node district model, thermal, battery and hydrogen storage, multiple commodities | No/not mentioned | Not mentioned (probably Euclidean/default for Matlab k-means) | k-means | Centroids | Maximum and minimum values of the demand profiles | Yes | No |
| 2019 | Hilbers et al. [166] | Single-node electricity model of Great Britain, no storage technologies | Yes, but not mentioned which | Euclidean | Samples (hourly). As benchmark: k-medoids (days) | Existing hours. As benchmark: medoids (days) | Yes with the method of subsampling and keeping the most expensive days | No | No |
| 2019 | Kannengießer et al. [140] | Multi-node district model and single-node island model, thermal, battery and hydrogen storage, multiple commodities | Min-max normalization | Euclidean | hierarchical | Medoids | No, but operation optimization for full time series | No | Yes |
| 2019 | Motlagh et al. [203] | Customer or unit partitioning/none (just approach) | No/not mentioned | Adjacency metric, in mapping parameter space: Euclidean d | Feature-based clustering or dynamic load-clustering | None | No | No | No |
| 2019 | Pavičević et al. [204] | Customer or unit partitioning/multi-node electricity model of the western Balkan, pumped hydro storage and CHP with thermal storage, (Dispa-SET) | No | None | By technology and location | Mean | No | No | No |
| 2019 | Pöstges et al. [187] | Single-node electricity model, no storage technologies, analytically solved as peak-load-pricing model | Yes, cap-specific costs | None | Segments in the duration curve implying use of different technologies (hours) | Sorted existing hours | Yes, by determining the capacity of each component from the merit order | No | Yes |
| 2019 | Savvidis et al. [80] | UC of dispatch electricity model for Germany, pumped hydro storage, (E2M2) | No | No | No | No | Certain time series qualities define intervals in which can be downsampled | Yes, by clustering adjacent periods | No |
| 2019 | Sun et al. [135] | Multi-node electricity model of Great Britain with intraday storage | Min-max normalization, dimensionality reduction applied | Euclidean | hierarchical | Medoids | No | No | No |
| 2019 | Teichgräber et al. [41] | Two minimal UC problems: An electricity storage model and a gas turbine dispatch model | Element-wise Z-Normalization | Euclidean, Dynamic Time Warping, Shape-based Distance | k-means k-medoids Barycenter Averaging k-shape hierarchical | Centroid, medoids | No | No | No |
| 2019 | Van der Heijde et al. [20] | Multi-node district heating model, thermal storage | No/not mentioned | L1-Norm | Using so-called “bins” | Existing days | No, but rearranging the typical days to the original sequence using a MIP | Yes | Yes |
| 2019 | Yokoyama et al. [68] | Building model for two hotels and four office buildings, no storage technologies, but multiple commodities | No | None | downsampling | Means | No | No | No |
| 2019 | Zatti et al. [141] | District model of Parma university campus and building model, thermal and battery storage, multiple commodities | Min-max normalization | Euclidean | (k-means, k-medoids) k-MILP (modification of k-medoids) | (Centroids), medoids | Automatically integrating atypical days | No | No |
| 2019 | Zhang et al. [161] | Single-node electricity model consisting of hydro, PV and wind power plants with reservoir storage | No/not mentioned | Euclidean | k-means | Means | No, but used Vine-Copula, ARMA-model and latin hypercube sampling to generate scenarios | No | No |
Appendix B
Customer and Unit Partitioning
Appendix C
Calculation Example for Time Series Normalization
References
- Robinius, M.; Otto, A.; Heuser, P.; Welder, L.; Syranidis, K.; Ryberg, D.S.; Grube, T.; Markewitz, P.; Peters, R.; Stolten, D. Linking the Power and Transport Sectors—Part 1: The Principle of Sector Coupling. Energies 2017, 10, 956. [Google Scholar] [CrossRef] [Green Version]
- Barnett, H.J. Energy Uses and Supplies 1950, 1947, 1965, Bureau of Mines: Washington, DC, USA, 1950.
- Boiteux, M. La Tarification des Demandes en Pointe. Rev. Gen. De L’electricite 1949, 58, 157–179. [Google Scholar]
- Boiteux, M. Peak-Load Pricing. J. Bus. 1960, 33, 157–179. [Google Scholar] [CrossRef]
- Steiner, P.O. Peak loads and efficient pricing. Q. J. Econ. 1957, 71, 585–610. [Google Scholar] [CrossRef]
- Sherali, H.D.; Soyster, A.L.; Murphy, F.H.; Sen, S. Linear programming based analysis of marginal cost pricing in electric utility capacity expansion. Eur. J. Oper. Res. 1982, 11, 349–360. [Google Scholar] [CrossRef]
- Helm, D. Energy policy: Security of supply, sustainability and competition. Energy Policy 2002, 30, 173–184. [Google Scholar] [CrossRef]
- Hoffman, K.C.; Wood, D.O. Energy System Modeling and Forecasting. Annu. Rev. Energy 1976, 1, 423–453. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Caramanis, M.C.; Tabors, R.D.; Nochur, K.S.; Schweppe, F.C. The Introduction of Non-Dispatchable Technologies as Decision Variables in Long-Term Generation Expansion Models. Ieee Power Eng. Rev. 1982, PER-2, 40–41. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Timilsina, G.R. A review of energy system models. Int. J. Energy Sect. Manag. 2010, 4, 494–518. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Ringkjøb, H.-K.; Haugan, P.M.; Solbrekke, I.M. A review of modelling tools for energy and electricity systems with large shares of variable renewables. Renew. Sustain. Energy Rev. 2018, 96, 440–459. [Google Scholar] [CrossRef]
- Kotzur, L.; Markewitz, P.; Robinius, M.; Stolten, D. Time series aggregation for energy system design: Modeling seasonal storage. Appl. Energy 2018, 213, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Gabrielli, P.; Gazzani, M.; Martelli, E.; Mazzotti, M. Optimal design of multi-energy systems with seasonal storage. Appl. Energy 2018, 219, 408–424. [Google Scholar] [CrossRef]
- Samsatli, S.; Samsatli, N.J. A general spatio-temporal model of energy systems with a detailed account of transport and storage. Comput. Chem. Eng. 2015, 80, 155–176. [Google Scholar] [CrossRef]
- Samsatli, S.; Staffell, I.; Samsatli, N.J. Optimal design and operation of integrated wind-hydrogen-electricity networks for decarbonising the domestic transport sector in Great Britain. Int. J. Hydrog. Energy 2016, 41, 447–475. [Google Scholar] [CrossRef]
- Welder, L.; Ryberg, D.; Kotzur, L.; Grube, T.; Robinius, M.; Stolten, D. Spatio-Temporal Optimization of a Future Energy System for Power-to-Hydrogen Applications in Germany. Energy 2018, 158, 1130–1149. [Google Scholar] [CrossRef]
- Tejada-Arango, D.A.; Domeshek, M.; Wogrin, S.; Centeno, E. Enhanced Representative Days and System States Modeling for Energy Storage Investment Analysis. IEEE Trans. Power Syst. 2018, 33, 6534–6544. [Google Scholar] [CrossRef] [Green Version]
- van der Heijde, B.; Vandermeulen, A.; Salenbien, R.; Helsen, L. Representative days selection for district energy system optimisation: A solar district heating system with seasonal storage. Appl. Energy 2019, 248, 79–94. [Google Scholar] [CrossRef]
- Ören, T.I. Computer-Aided Systems technology: Its role in advanced computerization. In Computer Aided Systems Theory; Pichler, F., Moreno Díaz, R., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 1994; pp. 11–20. [Google Scholar]
- Sass, S.; Mitsos, A. Optimal Operation of Dynamic (Energy) Systems: When are Quasi-Steady Models Adequate? Comput. Chem. Eng. 2019. [Google Scholar] [CrossRef]
- Morales-España, G.; Tejada-Arango, D. Modelling the Hidden Flexibility of Clustered Unit Commitment. IEEE Trans. Power Syst. 2018.
- Lara, C.L.; Mallapragada, D.S.; Papageorgiou, D.J.; Venkatesh, A.; Grossmann, I.E. Deterministic electric power infrastructure planning: Mixed-integer programming model and nested decomposition algorithm. Eur. J. Oper. Res. 2018, 271, 1037–1054. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Stolten, D.; Robinius, M. Cost Uncertainties in Energy System Optimisation Models: A Quadratic Programming Approach for Avoiding Penny Switching Effects. Energies 2019, 12, 4006. [Google Scholar] [CrossRef] [Green Version]
- Klinge Jacobsen, H. Integrating the bottom-up and top-down approach to energy–economy modelling: The case of Denmark. Energy Econ. 1998, 20, 443–461. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, A.; Gundersen, T.; Adams, T. Modeling and simulation of energy systems: A review. Processes 2018, 6, 238. [Google Scholar] [CrossRef] [Green Version]
- Böhringer, C.; Rutherford, T.F. Integrating bottom-up into top-down: A mixed complementarity approach. Zew-Cent. Eur. Econ. Res. Discuss. Pap. 2005, 05-028. [Google Scholar]
- Herbst, M.; Toro, F.; Reitze, F.; Eberhard, J. Bridging Macroeconomic and Bottom up Energy Models-the Case of Efficiency in Industry. EceeNeth. 2012. [Google Scholar]
- Helgesen, P.I. Top-down and Bottom-up: Combining energy system models and macroeconomic general equilibrium models. Censes: TrondheimNor. 2013. [Google Scholar]
- Schaller, R.R. Moore’s law: Past, present and future. Ieee Spectr. 1997, 34, 52–59. [Google Scholar] [CrossRef]
- Robison, R.A. Moore’s Law: Predictor and Driver of the Silicon Era. World Neurosurg. 2012, 78, 399–403. [Google Scholar] [CrossRef]
- Koch, T.; Martin, A.; Pfetsch, M.E. Progress in Academic Computational Integer Programming. In Facets of Combinatorial Optimization: Festschrift for Martin Grötschel; Jünger, M., Reinelt, G., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2013; pp. 483–506. [Google Scholar]
- Theis, T.N.; Wong, H.P. The End of Moore’s Law: A New Beginning for Information Technology. Comput. Sci. Eng. 2017, 19, 41–50. [Google Scholar] [CrossRef]
- Priesmann, J.; Nolting, L.; Praktiknjo, A. Are complex energy system models more accurate? An intra-model comparison of power system optimization models. Appl. Energy 2019, 255, 113783. [Google Scholar] [CrossRef]
- Poncelet, K.; Delarue, E.; Duerinck, J.; Six, D.; D’haeseleer, W. The Importance of Integrating the Variability of Renewables in Long-term Energy Planning Models; TME: Rome, Italy, 2014. [Google Scholar]
- Pfenninger, S. Dealing with multiple decades of hourly wind and PV time series in energy models: A comparison of methods to reduce time resolution and the planning implications of inter-annual variability. Appl. Energy 2017, 197, 1–13. [Google Scholar] [CrossRef]
- Stenzel, P.; Linssen, J.; Fleer, J.; Busch, F. Impact of temporal resolution of supply and demand profiles on the design of photovoltaic battery systems for increased self-consumption. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Mallapragada, D.S.; Papageorgiou, D.J.; Venkatesh, A.; Lara, C.L.; Grossmann, I.E. Impact of model resolution on scenario outcomes for electricity sector system expansion. Energy 2018, 163, 1231–1244. [Google Scholar] [CrossRef]
- Merrick, J.H. On representation of temporal variability in electricity capacity planning models. Energy Econ. 2016, 59, 261–274. [Google Scholar] [CrossRef] [Green Version]
- Teichgraeber, H.; Brandt, A.R. Clustering methods to find representative periods for the optimization of energy systems: An initial framework and comparison. Appl. Energy 2019, 239, 1283–1293. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brandt, A.R. Time Series Aggregation for the Optimization of Energy Systems: Goals, Challenges, Approaches, and Opportunities. Manuscr. Prep. 2019. [Google Scholar]
- Hall, L.M.H.; Buckley, A.R. A review of energy systems models in the UK: Prevalent usage and categorisation. Appl. Energy 2016, 169, 607–628. [Google Scholar] [CrossRef] [Green Version]
- Van der Voort, E. The EFOM 12C energy supply model within the EC modelling system. Omega 1982, 10, 507–523. [Google Scholar] [CrossRef]
- Kydes, A.S. The Brookhaven Energy System Optimization Model: Its Variants and Uses. In Energy Policy Modeling: United States and Canadian Experiences: Volume II Integrative Energy Policy Models; Ziemba, W.T., Schwartz, S.L., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1980; pp. 110–136. [Google Scholar]
- Loulou, R.; Kanudia, A.; Goldstein, G. Documentation for the times model part ii. Energy Technol. Syst. Anal. Programme. 2016. [Google Scholar]
- Loulou, R.; Goldstein, G.; Kanudia, A.; Lettila, A.; Remne, U. Documentation for the TIMES Model PART I; TIMES: London, UK, 2016. [Google Scholar]
- Loulou, R.; Remne, U.; Kanudia, A.; Lehtila, A.; Goldstein, G. Documentation for the TIMES Model PART I; TIMES: London, UK, 2005. [Google Scholar]
- Loulou, R.; Lehtilä, A.; Kanudia, A.; Remne, U.; Goldstein, G. Documentation for the TIMES Model PART II; TIMES: London, UK, 2005. [Google Scholar]
- Kannan, R. The development and application of a temporal MARKAL energy system model using flexible time slicing. Appl. Energy 2011, 88, 2261–2272. [Google Scholar] [CrossRef]
- Neniškis, E.; Galinis, A. Representation of wind power generation in economic models for long-term energy planning. Energetika 2018, 64. [Google Scholar] [CrossRef] [Green Version]
- Rosen, J. The Future Role of Renewable Energy Sources in European Electricity Supply: A Model-Based Analysis for the EU-15; KIT Scientific Publishing: Karlsruhe, Germany, 2008. [Google Scholar]
- Balachandra, P.; Chandru, V. Modelling electricity demand with representative load curves. Energy 1999, 24, 219–230. [Google Scholar] [CrossRef]
- Mavrotas, G.; Diakoulaki, D.; Florios, K.; Georgiou, P. A mathematical programming framework for energy planning in services’ sector buildings under uncertainty in load demand: The case of a hospital in Athens. Energy Policy 2008, 36, 2415–2429. [Google Scholar] [CrossRef]
- Domínguez-Muñoz, F.; Cejudo-López, J.M.; Carrillo-Andrés, A.; Gallardo-Salazar, M. Selection of typical demand days for CHP optimization. Energy Build. 2011, 43, 3036–3043. [Google Scholar] [CrossRef]
- Chen, C.; Ibekwe-SanJuan, F.; Hou, J. The structure and dynamics of cocitation clusters: A multiple-perspective cocitation analysis. J. Am. Soc. Inf. Sci. Technol. 2010, 61, 1386–1409. [Google Scholar] [CrossRef] [Green Version]
- Kotzur, L.; Markewitz, P.; Robinius, M.; Stolten, D. Impact of different time series aggregation methods on optimal energy system design. Renew. Energy 2018, 117, 474–487. [Google Scholar] [CrossRef] [Green Version]
- Schütz, T.; Schraven, M.; Fuchs, M.; Remmen, P.; Mueller, D. Comparison of clustering algorithms for the selection of typical demand days for energy system synthesis. Renew. energy 2018, 129, 570–582. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Seyed Shirkhorshidi, A.; Ying Wah, T. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Andrews, R.W.; Stein, J.S.; Hansen, C.; Riley, D. Introduction to the open source PV LIB for python Photovoltaic system modelling package. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 0170–0174. [Google Scholar]
- Renaldi, R.; Friedrich, D. Multiple time grids in operational optimisation of energy systems with short- and long-term thermal energy storage. Energy 2017, 133, 784–795. [Google Scholar] [CrossRef] [Green Version]
- Nanopoulos, A.; Alcock, R.; Manolopoulos, Y. Feature-based classification of time-series data. In Information Processing and Technology; Nikos, M., Stavros, D.N., Eds.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2001; pp. 49–61. [Google Scholar]
- Agapoff, S.; Pache, C.; Panciatici, P.; Warland, L.; Lumbreras, S. Snapshot selection based on statistical clustering for Transmission Expansion Planning. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Deane, J.P.; Drayton, G.; Gallachóir, B.Ó. The impact of sub-hourly modelling in power systems with significant levels of renewable generation. Appl. Energy 2014, 113, 152–158. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Yokoyama, R.; Hasegawa, Y.; Ito, K. A MILP decomposition approach to large scale optimization in structural design of energy supply systems. Energy Convers. Manag. 2002, 43, 771–790. [Google Scholar] [CrossRef]
- Yokoyama, R.; Shinano, Y.; Taniguchi, S.; Ohkura, M.; Wakui, T. Optimization of energy supply systems by MILP branch and bound method in consideration of hierarchical relationship between design and operation. Energy Convers. Manag. 2015, 92, 92–104. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, R.; Shinano, Y.; Wakayama, Y.; Wakui, T. Model reduction by time aggregation for optimal design of energy supply systems by an MILP hierarchical branch and bound method. Energy 2019, 181, 782–792. [Google Scholar] [CrossRef]
- Fazlollahi, S.; Bungener, S.L.; Mandel, P.; Becker, G.; Maréchal, F. Multi-objectives, multi-period optimization of district energy systems: I. Selection of typical operating periods. Comput. Chem. Eng. 2014, 65, 54–66. [Google Scholar] [CrossRef] [Green Version]
- Bungener, S.; Hackl, R.; Van Eetvelde, G.; Harvey, S.; Marechal, F. Multi-period analysis of heat integration measures in industrial clusters. Energy 2015, 93, 220–234. [Google Scholar] [CrossRef]
- Deml, S.; Ulbig, A.; Borsche, T.; Andersson, G. The role of aggregation in power system simulation. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Pineda, S.; Morales, J.M. Chronological Time-Period Clustering for Optimal Capacity Expansion Planning With Storage. IEEE Trans. Power Syst. 2018, 33, 7162–7170. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function AU-Ward, Joe H. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Bahl, B.; Söhler, T.; Hennen, M.; Bardow, A. Typical Periods for Two-Stage Synthesis by Time-Series Aggregation with Bounded Error in Objective Function. Front. Energy Res. 2018, 5. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Baumgärtner, N.; Temme, F.; Bahl, B.; Hennen, M.; Hollermann, D.; Bardow, A. RiSES4 Rigorous Synthesis of Energy Supply Systems with Seasonal Storage by Relaxation and Time—Series Aggregation to Typical Periods. In Proceedings of the ECOS 2019, Wroclaw, Poland, 23–28 June 2019. [Google Scholar]
- Baumgärtner, N.; Bahl, B.; Hennen, M.; Bardow, A. RiSES3: Rigorous Synthesis of Energy Supply and Storage Systems via time-series relaxation and aggregation. Comput. Chem. Eng. 2019, 127, 127–139. [Google Scholar] [CrossRef]
- Stein, D.V.; Bracht, N.V.; Maaz, A.; Moser, A. Development of adaptive time patterns for multi-dimensional power system simulations. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Georgios Savvidis, K.H. How well do we understand our power system models? In Proceedings of the 42nd International Association for Energy Economics (IAEE) Annual Conference, Montréal, QC, Canada, 29 May–1 June 2019.
- Bauer, D.; Marx, R.; Nußbicker-Lux, J.; Ochs, F.; Heidemann, W.; Müller-Steinhagen, H. German central solar heating plants with seasonal heat storage. Sol. Energy 2010, 84, 612–623. [Google Scholar] [CrossRef]
- Sorknæs, P. Simulation method for a pit seasonal thermal energy storage system with a heat pump in a district heating system. Energy 2018, 152, 533–538. [Google Scholar] [CrossRef]
- Wogrin, S.; Galbally, D.; Reneses, J. Optimizing Storage Operations in Medium-and Long-Term Power System Models. IEEE Trans. Power Syst. 2016, 31, 3129–3138. [Google Scholar] [CrossRef]
- Tejada-Arango, D.A.; Wogrin, S.; Centeno, E. Representation of Storage Operations in Network-Constrained Optimization Models for Medium- and Long-Term Operation. IEEE Trans. Power Syst. 2018, 33, 386–396. [Google Scholar] [CrossRef]
- Wogrin, S.; Dueñas, P.; Delgadillo, A.; Reneses, J. A New Approach to Model Load Levels in Electric Power Systems With High Renewable Penetration. IEEE Trans. Power Syst. 2014, 29, 2210–2218. [Google Scholar] [CrossRef]
- Härtel, P.; Kristiansen, M.; Korpås, M. Assessing the impact of sampling and clustering techniques on offshore grid expansion planning. Energy Procedia 2017, 137, 152–161. [Google Scholar] [CrossRef]
- Ploussard, Q.; Olmos, L.; Ramos, A. An operational state aggregation technique for transmission expansion planning based on line benefits. IEEE Trans. Power Syst. 2016, 32, 2744–2755. [Google Scholar] [CrossRef]
- Lythcke-Jørgensen, C.E.; Münster, M.; Ensinas, A.V.; Haglind, F. A method for aggregating external operating conditions in multi-generation system optimization models. Appl. Energy 2016, 166, 59–75. [Google Scholar] [CrossRef] [Green Version]
- Buoro, D.; Casisi, M.; Pinamonti, P.; Reini, M. Optimal synthesis and operation of advanced energy supply systems for standard and domotic home. Energy Convers. Manag. 2012, 60, 96–105. [Google Scholar] [CrossRef]
- Harb, H.; Schwager, C.; Streblow, R.; Mueller, D. Optimal design of energy systems in residential districts WITH interconnected local heating and electrical networks. In Proceedings of the 14th International IBPSA Conference, Hyderabad, India, 7–9 December 2015. [Google Scholar]
- Merkel, E.; McKenna, R.; Fichtner, W. Optimisation of the capacity and the dispatch of decentralised micro-CHP systems: A case study for the UK. Appl. Energy 2015, 140, 120–134. [Google Scholar] [CrossRef]
- de Sisternes, F.J.; Jenkins, J.D.; Botterud, A. The value of energy storage in decarbonizing the electricity sector. Appl. Energy 2016, 175, 368–379. [Google Scholar] [CrossRef] [Green Version]
- De Sisternes Jimenez, F.; Webster, M.D. Optimal Selection of Sample Weeks for Approximating the Net Load in Generation Planning Problems; Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Patteeuw, D.; Helsen, L. Combined design and control optimization of residential heating systems in a smart-grid context. Energy Build. 2016, 133, 640–657. [Google Scholar] [CrossRef]
- van der Heijde, B.; Scapino, L.; Vandermeulen, A.; Patteeuw, D.; Helsen, L.; Salenbien, R. Using Representative Time Slices for Optimization of Thermal Energy Storage Systems in Low-Temperature District Heating Systems. In Proceedings of the ECOS 2018 31st International Conference on Efficiency, Cost, Optimization, SImulation and Environmental Impact of Energy Systems, Guimarães, Portugal, 17–22 June 2018. [Google Scholar]
- Murty, M.N.; Jain, A.K.; Flynn, P. Data clustering: A review. ACM Comput Surv. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar]
- Brodrick, P.G.; Brandt, A.R.; Durlofsky, L.J. Optimal design and operation of integrated solar combined cycles under emissions intensity constraints. Appl. Energy 2018, 226, 979–990. [Google Scholar] [CrossRef]
- Marton, C.H.; Elkamel, A.; Duever, T.A. An order-specific clustering algorithm for the determination of representative demand curves. Comput. Chem. Eng. 2008, 32, 1365–1372. [Google Scholar] [CrossRef]
- Lozano, M.A.; Ramos, J.C.; Serra, L.M. Cost optimization of the design of CHCP (combined heat, cooling and power) systems under legal constraints. Energy 2010, 35, 794–805. [Google Scholar] [CrossRef]
- Schütz, T.; Schiffer, L.; Harb, H.; Fuchs, M.; Müller, D. Optimal design of energy conversion units and envelopes for residential building retrofits using a comprehensive MILP model. Appl. Energy 2017, 185, 1–15. [Google Scholar] [CrossRef]
- Harb, H.; Reinhardt, J.; Streblow, R.; Mueller, D. MIP approach for designing heating systems in residential buildings and neighbourhood. J. Build. Perform. Simul. 2015. [Google Scholar] [CrossRef]
- Kools, L.; Phillipson, F. Data granularity and the optimal planning of distributed generation. Energy 2016, 112, 342–352. [Google Scholar] [CrossRef] [Green Version]
- Voll, P.; Klaffke, C.; Hennen, M.; Bardow, A. Automated superstructure-based synthesis and optimization of distributed energy supply systems. Energy 2013, 50, 374–388. [Google Scholar] [CrossRef]
- Nicolosi, M. The Importance of High Temporal Resolution in Modeling Renewable Energy Penetration Scenarios; Lawrence Berkeley National Lab.(LBNL): Berkeley, CA, USA, 2010. [Google Scholar]
- Haydt, G.; Leal, V.; Pina, A.; Silva, C.A. The relevance of the energy resource dynamics in the mid/long-term energy planning models. Renew. Energy 2011, 36, 3068–3074. [Google Scholar] [CrossRef]
- Welsch, M.; Howells, M.; Bazilian, M.; DeCarolis, J.F.; Hermann, S.; Rogner, H.H. Modelling elements of Smart Grids—Enhancing the OSeMOSYS (Open Source Energy Modelling System) code. Energy 2012, 46, 337–350. [Google Scholar] [CrossRef]
- Timmerman, J.; Hennen, M.; Bardow, A.; Lodewijks, P.; Vandevelde, L.; Van Eetvelde, G. Towards low carbon business park energy systems: A holistic techno-economic optimisation model. Energy 2017, 125, 747–770. [Google Scholar] [CrossRef]
- Wakui, T.; Kawayoshi, H.; Yokoyama, R. Optimal structural design of residential power and heat supply devices in consideration of operational and capital recovery constraints. Appl. Energy 2016, 163, 118–133. [Google Scholar] [CrossRef]
- Wakui, T.; Yokoyama, R. Optimal structural design of residential cogeneration systems with battery based on improved solution method for mixed-integer linear programming. Energy 2015, 84, 106–120. [Google Scholar] [CrossRef]
- Wakui, T.; Yokoyama, R. Optimal structural design of residential cogeneration systems in consideration of their operating restrictions. Energy 2014, 64, 719–733. [Google Scholar] [CrossRef]
- Lozano, M.A.; Ramos, J.C.; Carvalho, M.; Serra, L.M. Structure optimization of energy supply systems in tertiary sector buildings. Energy Build. 2009, 41, 1063–1075. [Google Scholar] [CrossRef]
- Weber, C.; Shah, N. Optimisation based design of a district energy system for an eco-town in the United Kingdom. Energy 2011, 36, 1292–1308. [Google Scholar] [CrossRef]
- Stadler, M.; Groissböck, M.; Cardoso, G.; Marnay, C. Optimizing Distributed Energy Resources and building retrofits with the strategic DER-CAModel. Appl. Energy 2014, 132, 557–567. [Google Scholar] [CrossRef] [Green Version]
- Casisi, M.; Pinamonti, P.; Reini, M. Optimal lay-out and operation of combined heat & power (CHP) distributed generation systems. Energy 2009, 34, 2175–2183. [Google Scholar]
- Pina, A.; Silva, C.A.; Ferrão, P. High-resolution modeling framework for planning electricity systems with high penetration of renewables. Appl. Energy 2013, 112, 215–223. [Google Scholar] [CrossRef]
- Spiecker, S.; Vogel, P.; Weber, C. Evaluating interconnector investments in the north European electricity system considering fluctuating wind power penetration. Energy Econ. 2013, 37, 114–127. [Google Scholar] [CrossRef]
- Wouters, C.; Fraga, E.S.; James, A.M. An energy integrated, multi-microgrid, MILP (mixed-integer linear programming) approach for residential distributed energy system planning—A South Australian case-study. Energy 2015, 85, 30–44. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Zhang, S.; Xiao, Y. Optimal design of distributed energy resource systems coupled with energy distribution networks. Energy 2015, 85, 433–448. [Google Scholar] [CrossRef]
- Ameri, M.; Besharati, Z. Optimal design and operation of district heating and cooling networks with CCHP systems in a residential complex. Energy Build. 2016, 110, 135–148. [Google Scholar] [CrossRef]
- Bracco, S.; Dentici, G.; Siri, S. DESOD: A mathematical programming tool to optimally design a distributed energy system. Energy 2016, 100, 298–309. [Google Scholar] [CrossRef]
- Moradi, S.; Ghaffarpour, R.; Ranjbar, A.M.; Mozaffari, B. Optimal integrated sizing and planning of hubs with midsize/large CHP units considering reliability of supply. Energy Convers. Manag. 2017, 148, 974–992. [Google Scholar] [CrossRef]
- Swider, D.J.; Weber, C. The costs of wind’s intermittency in Germany: Application of a stochastic electricity market model. Eur. Trans. Electr. Power 2007, 17, 151–172. [Google Scholar] [CrossRef]
- Oluleye, G.; Vasquez, L.; Smith, R.; Jobson, M. A multi-period Mixed Integer Linear Program for design of residential distributed energy centres with thermal demand data discretisation. Sustain. Prod. Consum. 2016, 5, 16–28. [Google Scholar] [CrossRef]
- Pina, A.; Silva, C.; Ferrão, P. Modeling hourly electricity dynamics for policy making in long-term scenarios. Energy Policy 2011, 39, 4692–4702. [Google Scholar] [CrossRef]
- Devogelaer, D. Towards 100% Renewable Energy in Belgium by 2050; FPB: Brussels¸ Belgium, 2012. [Google Scholar]
- Kannan, R.; Turton, H. A Long-Term Electricity Dispatch Model with the TIMES Framework. Environ. Model. Assess. 2013, 18, 325–343. [Google Scholar] [CrossRef] [Green Version]
- Simões, S.; Nijs, W.; Ruiz, P.; Sgobbi, A.; Radu, D.; Yilmaz Bolat, P.; Thiel, C.; Peteves, E. The JRC-EU-TIMES model—Assessing the long-term role of the SET Plan Energy technologies. JRC’s Inst. Energy Transport Tech. Rep. 2013. [Google Scholar]
- Poncelet, K.; Delarue, E.; Six, D.; Duerinck, J.; D’haeseleer, W. Impact of the level of temporal and operational detail in energy-system planning models. Appl. Energy 2016, 162, 631–643. [Google Scholar] [CrossRef] [Green Version]
- Mehleri, E.D.; Sarimveis, H.; Markatos, N.C.; Papageorgiou, L.G. A mathematical programming approach for optimal design of distributed energy systems at the neighbourhood level. Energy 2012, 44, 96–104. [Google Scholar] [CrossRef]
- Mehleri, E.D.; Sarimveis, H.; Markatos, N.C.; Papageorgiou, L.G. Optimal design and operation of distributed energy systems: Application to Greek residential sector. Renew. Energy 2013, 51, 331–342. [Google Scholar] [CrossRef]
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When Is “Nearest Neighbor” Meaningful? In Proceedings of the Database Theory—ICDT’99; Beeri, C., Buneman, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 217–235. [Google Scholar]
- Keogh, E.; Mueen, A. Curse of Dimensionality. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer US: Boston, MA, USA, 2010; pp. 257–258. [Google Scholar]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the Surprising Behavior of Distance Metrics in High Dimensional Space. In Proceedings of the Database Theory—ICDT 2001; Van den Bussche, J., Vianu, V., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved Deep Embedded Clustering with Local Structure Preservation. In Proceedings of the 26th International Joint Conference on Artificial Intelligence; AAAI Press: Melbourne, Australia, 2017; pp. 1753–1759. [Google Scholar]
- Sun, M.; Teng, F.; Zhang, X.; Strbac, G.; Pudjianto, D. Data-Driven Representative Day Selection for Investment Decisions: A Cost-Oriented Approach. IEEE Trans. Power Syst. 2019, 34, 1. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Konstantelos, I.; Strbac, G. C-Vine Copula Mixture Model for Clustering of Residential Electrical Load Pattern Data. IEEE Trans. Power Syst. 2017, 32, 2382–2393. [Google Scholar] [CrossRef] [Green Version]
- Almaimouni, A.; Ademola-Idowu, A.; Nathan Kutz, J.; Negash, A.; Kirschen, D. Selecting and Evaluating Representative Days for Generation Expansion Planning. In 2018 Power Systems Computation Conference; IEEE: Piscataway Township, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Fazlollahi, S.; Girardin, L.; Maréchal, F. Clustering Urban Areas for Optimizing the Design and the Operation of District Energy Systems. In Computer Aided Chemical Engineering; Klemeš, J.J., Varbanov, P.S., Liew, P.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 33, pp. 1291–1296. [Google Scholar]
- Schütz, T.; Schraven, M.; Harb, H.; Fuchs, M.; Mueller, D. Clustering Algorithms for the Selection of Typical Demand Days for the Optimal Design of Building Energy Systems. In Proceedings of the ECOS 2016: 29th International Conference on Efficiency, Cost, Optimization, Simulation, and Environmental Impact of Energy Systems, Portoroz, Slovenia, 16–23 June 2016. [Google Scholar]
- Kannengießer, T.; Hoffmann, M.; Kotzur, L.; Stenzel, P.; Schuetz, F.; Peters, K.; Nykamp, S.; Stolten, D.; Robinius, M. Reducing Computational Load for Mixed Integer Linear Programming: An Example for a District and an Island Energy System. Energies 2019, 12, 2825. [Google Scholar] [CrossRef] [Green Version]
- Zatti, M.; Gabba, M.; Freschini, M.; Rossi, M.; Gambarotta, A.; Morini, M.; Martelli, E. k-MILP: A novel clustering approach to select typical and extreme days for multi-energy systems design optimization. Energy 2019, 181, 1051–1063. [Google Scholar] [CrossRef]
- Fitiwi, D.Z.; de Cuadra, F.; Olmos, L.; Rivier, M. A new approach of clustering operational states for power network expansion planning problems dealing with RES (renewable energy source) generation operational variability and uncertainty. Energy 2015, 90, 1360–1376. [Google Scholar] [CrossRef]
- Nahmmacher, P.; Schmid, E.; Hirth, L.; Knopf, B. Carpe diem: A novel approach to select representative days for long-term power system modeling. Energy 2016, 112, 430–442. [Google Scholar] [CrossRef]
- Poncelet, K.; Höschle, H.; Delarue, E.; Virag, A.; D’haeseleer, W. Selecting Representative Days for Capturing the Implications of Integrating Intermittent Renewables in Generation Expansion Planning Problems. IEEE Trans. Power Syst. 2016, 32, 1936–1948. [Google Scholar] [CrossRef] [Green Version]
- Voulis, N.; Warnier, M.; Brazier, F.M.T. Understanding spatio-temporal electricity demand at different urban scales: A data-driven approach. Appl. Energy 2018, 230, 1157–1171. [Google Scholar] [CrossRef]
- Brodrick, P.G.; Brandt, A.R.; Durlofsky, L.J. Operational optimization of an integrated solar combined cycle under practical time-dependent constraints. Energy 2017, 141, 1569–1584. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brodrick, P.G.; Brandt, A.R. Optimal design and operations of a flexible oxyfuel natural gas plant. Energy 2017, 141, 506–518. [Google Scholar] [CrossRef]
- Liu, Y.; Sioshansi, R.; Conejo, A.J. Hierarchical Clustering to Find Representative Operating Periods for Capacity-Expansion Modeling. IEEE Trans. Power Syst. 2018, 33, 3029–3039. [Google Scholar] [CrossRef]
- Marquant, J.; Omu, A.; Evins, R.; Carmeliet, J. Application of Spatial-Temporal Clustering to Facilitate Energy System Modelling. In 14th International Confrence of IBPSA Building Simulation 2015; Khare, V.R., Gaurav, C., Eds.; IIIT Hyderabad: Hyderabad, India, 2015; pp. 551–558. [Google Scholar]
- Marquant, J.F.; Mavromatidis, G.; Evins, R.; Carmeliet, J. Comparing different temporal dimension representations in distributed energy system design models. Energy Procedia 2017, 122, 907–912. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C.-T. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef] [Green Version]
- Adhau, S.P.; Moharil, R.M.; Adhau, P.G. K-Means clustering technique applied to availability of micro hydro power. Sustain. Energy Technol. Assess. 2014, 8, 191–201. [Google Scholar] [CrossRef]
- Green, R.; Staffell, I.; Vasilakos, N. Divide and Conquer? k-Means Clustering of Demand Data Allows Rapid and Accurate Simulations of the British Electricity System. IEEE Trans. Eng. Manag. 2014, 61, 251–260. [Google Scholar] [CrossRef]
- Brodrick, P.G.; Kang, C.A.; Brandt, A.R.; Durlofsky, L.J. Optimization of carbon-capture-enabled coal-gas-solar power generation. Energy 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Lin, F.; Leyffer, S.; Munson, T. A two-level approach to large mixed-integer programs with application to cogeneration in energy-efficient buildings. Comput. Optim. Appl. 2016, 65, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Bahl, B.; Kümpel, A.; Seele, H.; Lampe, M.; Bardow, A. Time-series aggregation for synthesis problems by bounding error in the objective function. Energy 2017, 135, 900–912. [Google Scholar] [CrossRef]
- Heuberger, C.F.; Staffell, I.; Shah, N.; Dowell, N.M. A systems approach to quantifying the value of power generation and energy storage technologies in future electricity networks. Comput. Chem. Eng. 2017, 107, 247–256. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brandt, A.R. Systematic Comparison of Aggregation Methods for Input Data Time Series Aggregation of Energy Systems Optimization Problems. In Computer Aided Chemical Engineering; Eden, M.R., Ierapetritou, M.G., Towler, G.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 44, pp. 955–960. [Google Scholar]
- Gabrielli, P.; Fürer, F.; Mavromatidis, G.; Mazzotti, M. Robust and optimal design of multi-energy systems with seasonal storage through uncertainty analysis. Appl. Energy 2019, 238, 1192–1210. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Hu, W.; Wang, Y.; Dong, L.; Zhang, J. Coordinated optimal operation of hydro–wind–solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 1027–1035. [Google Scholar]
- Schiefelbein, J.; Tesfaegzi, J.; Streblow, R.; Müller, D. Design of an optimization algorithm for the distribution of thermal energy systems and local heating networks within a city district. Proc. Ecos 2015. [Google Scholar]
- Zhu, Q.; Luo, X.; Zhang, B.; Chen, Y. Mathematical modelling and optimization of a large-scale combined cooling, heat, and power system that incorporates unit changeover and time-of-use electricity price. Energy Convers. Manag. 2017, 133, 385–398. [Google Scholar] [CrossRef]
- Stadler, P.; Girardin, L.; Ashouri, A.; Maréchal, F. Contribution of Model Predictive Control in the Integration of Renewable Energy Sources within the Built Environment. Front. Energy Res. 2018, 6. [Google Scholar] [CrossRef] [Green Version]
- Hilbers, A.P.; Brayshaw, D.J.; Gandy, A. Importance subsampling: Improving power system planning under climate-based uncertainty. Appl. Energy 2019, 251, 113114. [Google Scholar] [CrossRef] [Green Version]
- Tupper, L.L.; Matteson, D.S.; Anderson, C.L.; Zephyr, L. Band Depth Clustering for Nonstationary Time Series and Wind Speed Behavior. Technometrics 2018, 60, 245–254. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, L.; Rousseeuw, P.J. Clustering by means of medoids. Statistical Data Analysis based on the L1 Norm. Y. DodgeEd 1987, 405–416. [Google Scholar]
- Vinod, H. Integer Programming and the Theory of Grouping. J. Am. Stat. Assoc. 1969, 64. [Google Scholar] [CrossRef]
- Singh, A.; Yadav, A.; Rana, A. K-means with Three different Distance Metrics. Int. J. Comput. Appl. 2013, 67. [Google Scholar] [CrossRef]
- Bradley, P.S.; Mangasarian, O.L.; Street, W.N. Clustering via concave minimization. In Advances in Neural Information Processing Systems; Mit Press: Cambridge, MA, USA, 1997; pp. 368–374. [Google Scholar]
- Whelan, C.; Harrell, G.; Wang, J. Understanding the K-Medians Problem. In Proceedings of the International Conference on Scientific Computing (CSC), The Steering Committee of The World Congress in Computer Science, Computer, San Diego, CA, USA, 27–30 July 2015; p. 219. [Google Scholar]
- Har-Peled, S. Geometric Approximation Algorithms; American Mathematical Soc.: Providence, RI USA, 2006. [Google Scholar]
- Paparrizos, J.; Gravano, L. k-Shape: Efficient and Accurate Clustering of Time Series. Sigmod Rec. 2016, 45, 69–76. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Niennattrakul, V.; Srisai, D.; Ratanamahatana, C. Shape-based template matching for time series data. Knowl.-Based Syst. 2012, 26. [Google Scholar] [CrossRef]
- Poncelet, K.; Höschle, H.; Delarue, E.; D’haeseleer, W. Selecting Representative Days for Investment Planning Models; kU Leuven: Leuven, Belgium, 2015. [Google Scholar]
- Tveit, T.-M.; Savola, T.; Gebremedhin, A.; Fogelholm, C.-J. Multi-period MINLP model for optimising operation and structural changes to CHP plants in district heating networks with long-term thermal storage. Energy Convers. Manag. 2009, 50, 639–647. [Google Scholar] [CrossRef]
- Ortiga, J.; Bruno, J.C.; Coronas, A. Selection of typical days for the characterisation of energy demand in cogeneration and trigeneration optimisation models for buildings. Energy Convers. Manag. 2011, 52, 1934–1942. [Google Scholar] [CrossRef]
- van der Weijde, A.H.; Hobbs, B.F. The economics of planning electricity transmission to accommodate renewables: Using two-stage optimisation to evaluate flexibility and the cost of disregarding uncertainty. Energy Econ. 2012, 34, 2089–2101. [Google Scholar] [CrossRef]
- Munoz, F.D.; Mills, A.D. Endogenous Assessment of the Capacity Value of Solar PV in Generation Investment Planning Studies. IEEE Trans. Sustain. Energy 2015, 6, 1574–1585. [Google Scholar] [CrossRef] [Green Version]
- Frew, B.A.; Jacobson, M.Z. Temporal and spatial tradeoffs in power system modeling with assumptions about storage: An application of the POWER model. Energy 2016, 117, 198–213. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.-Y.; Chen, C.-L. Unit commitment with probabilistic reserve: An IPSO approach. Energy Convers. Manag. 2007, 48, 486–493. [Google Scholar] [CrossRef]
- Phan, Q.A.; Scully, T.; Breen, M.; Murphy, M.D. Determination of optimal battery utilization to minimize operating costs for a grid-connected building with renewable energy sources. Energy Convers. Manag. 2018, 174, 157–174. [Google Scholar] [CrossRef]
- Saravanan, B.; Das, S.; Sikri, S.; Kothari, D.P. A solution to the unit commitment problem—A review. Front. Energy 2013, 7, 223–236. [Google Scholar] [CrossRef]
- Xiao, J.; Bai, L.; Li, F.; Liang, H.; Wang, C. Sizing of Energy Storage and Diesel Generators in an Isolated Microgrid Using Discrete Fourier Transform (DFT). IEEE Trans. Sustain. Energy 2014, 5, 907–916. [Google Scholar] [CrossRef]
- Pöstges, A.; Weber, C. Time series aggregation—A new methodological approach using the “peak-load-pricing” model. Util. Policy 2019, 59, 100917. [Google Scholar] [CrossRef]
- Billington, R.; Allan, R.N. Reliability Evaluation of Power Systems; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Short, W.; Sullivan, P.; Mai, T.; Mowers, M.; Uriarte, C.; Blair, N.; Heimiller, D.; Martinez, A. Regional Energy Deployment System (ReEDS); National Renewable Energy Lab.(NREL): Golden, CO, USA, 2011. [Google Scholar]
- Frew, B.A.; Becker, S.; Dvorak, M.J.; Andresen, G.B.; Jacobson, M.Z. Flexibility mechanisms and pathways to a highly renewable US electricity future. Energy 2016, 101, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Scott, I.J.; Carvalho, P.M.S.; Botterud, A.; Silva, C.A. Clustering representative days for power systems generation expansion planning: Capturing the effects of variable renewables and energy storage. Appl. Energy 2019, 253, 113603. [Google Scholar] [CrossRef]
- Bahl, B.; Lützow, J.; Shu, D.; Hollermann, D.E.; Lampe, M.; Hennen, M.; Bardow, A. Rigorous synthesis of energy systems by decomposition via time-series aggregation. Comput. Chem. Eng. 2018, 112, 70–81. [Google Scholar] [CrossRef]
- Conejo, A.J.; Castillo, E.; Minguez, R.; Garcia-Bertrand, R. Decomposition Techniques in Mathematical Programming: Engineering and Science Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Schwele, A.; Kazempour, J.; Pinson, P. Do unit commitment constraints affect generation expansion planning? A scalable stochastic model. Energy Syst. 2019. [Google Scholar] [CrossRef]
- Pavičević, M.; Kavvadias, K.; Pukšec, T.; Quoilin, S. Comparison of different model formulations for modelling future power systems with high shares of renewables—The Dispa-SET Balkans model. Appl. Energy 2019, 252, 113425. [Google Scholar] [CrossRef]
- Alzate, C.; Espinoza, M.; De Moor, B.; Suykens, J.A.K. Identifying Customer Profiles in Power Load Time Series Using Spectral Clustering. In Artificial Neural Networks–ICANN 2009; Alippi, C., Polycarpou, M., Panayiotou, C., Ellinas, G., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2009; pp. 315–324. [Google Scholar]
- Benítez, I.; Quijano, A.; Díez, J.-L.; Delgado, I. Dynamic clustering segmentation applied to load profiles of energy consumption from Spanish customers. Int. J. Electr. Power Energy Syst. 2014, 55, 437–448. [Google Scholar] [CrossRef]
- Yang, J.; Ning, C.; Deb, C.; Zhang, F.; Cheong, D.; Lee, S.E.; Sekhar, C.; Tham, K.W. k-Shape clustering algorithm for building energy usage patterns analysis and forecasting model accuracy improvement. Energy Build. 2017, 146, 27–37. [Google Scholar] [CrossRef]
- Motlagh, O.; Berry, A.; O’Neil, L. Clustering of residential electricity customers using load time series. Appl. Energy 2019, 237, 11–24. [Google Scholar] [CrossRef]
- Haikarainen, C.; Pettersson, F.; Saxén, H. A decomposition procedure for solving two-dimensional distributed energy system design problems. Appl. Therm. Eng. 2016, 100, 30–38. [Google Scholar] [CrossRef]
- Grigg, C.; Wong, P.; Albrecht, P.; Allan, R.; Bhavaraju, M.; Billinton, R.; Chen, Q.; Fong, C.; Haddad, S.; Kuruganty, S. The IEEE reliability test system-1996. A report prepared by the reliability test system task force of the application of probability methods subcommittee. IEEE Trans. Power Syst. 1999, 14, 1010–1020. [Google Scholar] [CrossRef]
- Haller, M.; Ludig, S.; Bauer, N. Decarbonization scenarios for the EU and MENA power system: Considering spatial distribution and short term dynamics of renewable generation. Energy Policy 2012, 47, 282–290. [Google Scholar] [CrossRef]
- Stiphout, A.V.; Vos, K.D.; Deconinck, G. The Impact of Operating Reserves on Investment Planning of Renewable Power Systems. IEEE Trans. Power Syst. 2017, 32, 378–388. [Google Scholar] [CrossRef]
- Baumgärtner, N.; Delorme, R.; Hennen, M.; Bardow, A. Design of low-carbon utility systems: Exploiting time-dependent grid emissions for climate-friendly demand-side management. Appl. Energy 2019, 247, 755–765. [Google Scholar] [CrossRef]














| Term | Synonym (Term in This Review) | Definition | Keywords Used for Literature Research |
|---|---|---|---|
| Clustering (of Time Series) | Grouping, (Clustering) | “Given a dataset of n time series data , the process of unsupervised partitioning of into in such a way that homogeneous time series data are grouped together based on a certain similarity measure” [59] | Clustering |
| Complexity Reduction | None, (Complexity Reduction) | Different techniques to increase the computational tractability of ESMs [35] | Complexity Reduction |
| Energy System Model | Energy System Optimization Model, (Energy System Model) | A model “the analysis of existing national energy systems, as well as the prediction of potential future scenarios, is usually performed with” [9] | Energy System Optimization Model, Energy System Model |
| Period | None, (Period) | A group of consecutive time steps describing a regular amount of time (e.g., 24 h) | Typical Period |
| Representative | Typical, (Typical) | A single time step or a period representing a group of time steps or periods determined by clustering | Representative Day, Representative Week |
| Sample | None, (Sample) | A single time step or period taken from the original time series | Sampling, Random Sampling, Subsampling |
| Snapshot | System State, Time Step, (Time Step, If subset of TS: Typical Time Step) | A term used in the literature for typical time steps (TTS) | Snapshot |
| System State | Snapshot, Time Step, (Time Step, If subset of TS: Typical Time Step) | A term misleadingly used in the literature for typical time steps (TTS). It actually describes the state of a system under both external conditions (e.g., capacity factors) and internal state variables (e.g., storage levels) at a specific time step | System State |
| Temporal Resolution | None, (Temporal Resolution) | The resolution of a discretized time series given by the length of its time steps | Temporal Resolution |
| Time Series Aggregation | Temporal Aggregation, (Time Series Aggregation | In the narrow sense: The reduction of time steps in time series In a broader sense: The reduction of the number of time steps or time series | Time Series Aggregation, Temporal Aggregation |
| Time Slice | Time Slot, (Time Slice) | Hierarchically merged time steps appearing in a systematic order as used by the TIMES framework | Time Slice |
| Time Step | Snapshot System State (Time Step) | The smallest possible time interval of a discrete time series represented by a single value for each attribute | Time Step Typical Time Step |
| Typical | Representative (Typical) | Periods or single time steps considered to capture the basic characteristics of the external operating conditions of an energy system are named “typical” | Typical Day Typical Week |
| Sets & Indices | |
|---|---|
| Set | |
| Set/Index of Attributes | , |
| Set/Index of Time Steps | , |
| Set/Index of Periods | , |
| Set/Index of Inner-Period Time Steps | , |
| Set/Index of Cluster Members | , |
| Cluster Center (as Defined) | |
| Discrete Value of Time Series (Normed) | |
| Number of Items in a Set | |
| Matrix Path for Dynamic Time Warping | |
| Minkowski Exponent |
| Period Merging Type | Resolution Variation | Typical Periods |
|---|---|---|
| Time-based | Downsampling | Time Slices and Averaging |
| Feature-based | Segmentation | Clustering |
| Period Merging Type | Resolution Variation | Typical Periods |
|---|---|---|
| Time-Based | Downsampling - Does not exploit repeating time series patterns - Does not differentiate between more and less variant sections of the time series | Time Slices and Averaging + Exploits repeating time series patterns - Based on the modeler’s experience - Does not merge similar adjacent time steps |
| Feature-Based | Segmentation - Does not exploit repeating time series patterns + Differentiates between more and less variant sections of the time series | Clustering + Exploits repeating time series patterns + Automatic identification of similar patterns - Does not merge similar adjacent time steps |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, M.; Kotzur, L.; Stolten, D.; Robinius, M. A Review on Time Series Aggregation Methods for Energy System Models. Energies 2020, 13, 641. https://doi.org/10.3390/en13030641
Hoffmann M, Kotzur L, Stolten D, Robinius M. A Review on Time Series Aggregation Methods for Energy System Models. Energies. 2020; 13(3):641. https://doi.org/10.3390/en13030641
Chicago/Turabian StyleHoffmann, Maximilian, Leander Kotzur, Detlef Stolten, and Martin Robinius. 2020. "A Review on Time Series Aggregation Methods for Energy System Models" Energies 13, no. 3: 641. https://doi.org/10.3390/en13030641