Abstract
The psychological and statistical literature contains several proposals for calculating and plotting confidence intervals (CIs) for within-subjects (repeated measures) ANOVA designs. A key distinction is between intervals supporting inference about patterns of means (and differences between pairs of means, in particular) and those supporting inferences about individual means. In this report, it is argued that CIs for the former are best accomplished by adapting intervals proposed by Cousineau (Tutorials in Quantitative Methods for Psychology, 1, 42–45, 2005) and Morey (Tutorials in Quantitative Methods for Psychology, 4, 61–64, 2008) so that nonoverlapping CIs for individual means correspond to a confidence for their difference that does not include zero. CIs for the latter can be accomplished by fitting a multilevel model. In situations in which both types of inference are of interest, the use of a two-tiered CI is recommended. Free, open-source, cross-platform software for such interval estimates and plots (and for some common alternatives) is provided in the form of R functions for one-way within-subjects and two-way mixed ANOVA designs. These functions provide an easy-to-use solution to the difficult problem of calculating and displaying within-subjects CIs.
Similar content being viewed by others
There is now widespread agreement among experts that confidence intervals (CIs) should replace or supplement the reporting of p values in psychology (e.g., American Psychological Association, 2010; Dienes, 2008; Loftus, 2001; Rozeboom, 1960; Wilkinson & Task Force on Statistical Inference, 1999). What limited empirical data there are (Fidler & Loftus, 2009) suggest that CIs are easier to interpret than p values (e.g., reducing common misinterpretations associated with significance tests). In addition, there are a number of statistical arguments in favour of reporting CIs—the chief one being that they are more informative, because they convey information about both the magnitude of an effect and the precision with which it has been estimated (Baguley, 2009; Loftus, 2001). Not all of the arguments in favour of reporting CIs are statistical. Even advocates of null-hypothesis significance tests have suggested that such tests are overused, leading to “p value clutter” (Abelson, 1995, p. 77). A plot of means with CIs could replace many of the less interesting omnibus tests and pairwise comparisons that routinely accompany ANOVA.
Despite this near consensus, it is not uncommon for statistical summaries to be limited to point estimates—even for the most important effects. A major barrier to reporting CIs is lack of understanding among researchers of how to calculate an appropriate interval estimate where more than a single parameter estimate is involved. Cumming and Finch (2005) explored some of these barriers, providing guidance on how to calculate, report, and interpret CIs (with emphasis on the graphical presentation of means in a two-independent-group design). The difficulties they addressed are even more acute when more than two means are of interest or with within-subjects (repeated measures) designs.
In this article, I review the problem of constructing within-subjects CIs for ANOVA, consider the additional problem of displaying the interval, review the main solutions that have been proposed, and propose guidelines for calculating and displaying appropriate CIs. These solutions are implemented in the software environment R for a one-way design, making it easy to both obtain and plot suitable intervals. R is free, open source, and runs on Mac, Linux, and Windows operating systems (R Development Core Team, 2009). This program removes a barrier to the reporting of within-subjects CIs: Few of the commonly proposed solutions are implemented in readily available software.
Within-subject confidence intervals: the nature of the problem
First, consider the simple case of constructing and plotting a CI around a single mean. In a typical application, the variance is unknown and the interval estimate is formed using the t distribution. Both the CI and the formally equivalent one-sample t test assume that data are sampled from a population with normally distributed, independent errors.Footnote 1 For a sample of size n, a two-sided CI with 100(1 − α)% confidence takes the form
where \( \hat{\mu } \) is the sample mean (and an estimate of the population mean μ), \( {t_{{n - 1,1 - \alpha /2}}} \) is the critical value of the t distribution, and \( {\hat{\sigma }_{{\hat{\mu }}}} \) is the standard error of the mean estimated from the sample standard deviation \( \hat{\sigma }\;({\text{i}}{\text{.e}}.,\;{\hat{\sigma }_{{\hat{\mu }}}} = \hat{\sigma }/\sqrt {n} ) \). The margin of error (CI half-width) of this interval is therefore a multiple of the standard error of the parameter estimate. For intervals based on the t distribution, this multiple depends on (a) sample size and (b) the desired level of confidence. The sample size has an impact on both \( {\hat{\sigma }_{{\hat{\mu }}}} \) and the critical value of t, but its impact on the latter is often negligible unless n is small (and for a 95% CI, the multiplier t n–1,.975 approaches z .975 = 1.96 for any large sample).
In practice, researchers are often interested in comparing several means. ANOVA is the most common statistical procedure employed for this purpose. The additional complexity of dealing with several independent means produces several challenges. Even for the simple case of two independent means (which reduces to an independent t test), there are two main ways to plot an appropriate CI. The first option is to plot a CI for each population mean [e.g., using Eq. 1]. The second option is to plot a CI for the difference in population means. For independent means μ 1 and μ 2, sampled from a normal distribution with unknown variance, the CI for their difference takes the form
where n 1 and n 2 are the sizes of the two samples and \( {\hat{\sigma }_{{{{\hat{\mu }}_1} - {{\hat{\mu }}_2}}}} \) is the standard error of the difference. This quantity is typically estimated from the pooled standard deviation of the samples as \( {\hat{\sigma }_{{{{\hat{\mu }}_1} - {{\hat{\mu }}_2}}}} = {\hat{\sigma }_{\text{pooled}}}\sqrt {{1/{n_1} + 1/{n_2}}} \). The only additional assumption (at this stage) is that the population variances of the two groups are equal (i.e., \( \sigma_1^2 = \sigma_2^2 \)). A crucial observation is that the standard error of the difference is larger than the standard errors of the two means (\( {\hat{\sigma }_{{{{\hat{\mu }}_1}}}} \) and \( {\hat{\sigma }_{{{{\hat{\mu }}_2}}}} \)). This follows from the variance sum law, which relates the sum or difference of two variables to their respective variances. For the variance of a difference, the relationship can be stated as
where \( {\sigma_{{{X_1},{X_2}}}} \) is the covariance between the two variables. Because the covariance is zero when the groups are independent, \( \sigma_{{{x_1} - {x_2}}}^2 \) reduces to \( \sigma_1^2 + \sigma_2^2 \), and it follows that the standard deviation of a difference is \( \sqrt {{\sigma_1^2 + \sigma_2^2}} \). If the variances are also equal, it is trivial to show that the standard error of a difference between independent means is \( \sqrt {2} \) times larger than that of either of the separate means (each standard error being a simple function of σ when n is fixed). Thus, if sample sizes and variances are approximately equal, it is not unreasonable to work on the basis that the standard error of any difference is around \( \sqrt {2} \) larger than the standard error for an individual parameter (Schenker & Gentleman, 2001).
This discrepancy presents problems when deciding what to plot if more than one parameter (e.g., mean) is involved. Inference with a CI is usually accomplished merely by determining whether the interval contains or does not contain a parameter value of interest (e.g., zero). This practice mimics a null-hypothesis significance test, but does not make use of the additional information a CI delivers. A better starting point is to treat values within the interval as plausible values of the parameter, and values outside the interval as implausible values (Cumming & Finch, 2005; Loftus, 2001).Footnote 2 Thus, the CI can be interpreted with respect to a range of potentially plausible parameter values, rather than restricting interest to a single value. This is very important when considering the practical significance of an effect (Baguley, 2009). For instance, a CI that excludes zero may be statistically significant, but may not include any effect sizes that are practically significant. Likewise, a CI that includes zero may be statistically nonsignificant, but the effect cannot be interpreted as negligible unless it also excludes nonnegligible effect sizes.
If the margin of error around each individual mean computed from Eq. 1 is equal to 10, then the margin of error around a difference between independent means will be in the region of \( \sqrt {2} \times 10 \approx 14 \) (assuming similar sample sizes and variances). If the separate intervals overlap by some minuscule quantity, then the total distance between them will be approximately \( 10 + 10 = 20 \). Since this gap is larger than 14, it is implausible, according to Eq. 2, that the true difference is zero. Plotting intervals around the individual means using Eq. 1 will be misleading (e.g., if the overlapping CIs are erroneously interpreted as suggesting that the true difference might plausibly be zero).
It is possible to apply rules of thumb about the proportion of overlap to avoid these sorts of errors or to adjust a graphical display to deal with these problems (Cumming & Finch, 2005; Schenker & Gentleman, 2001). Furthermore, depending on the primary focus of inference, it is reasonable to plot the quantity of interest—whether individual means or their difference—with an appropriate CI. This is relatively easy with only two means, but with three or more means it becomes harder. For instance, a plot of all of the differences between a set of means can be hard to interpret. Patterns that are obvious when plotting separate means (e.g., increasing or decreasing trends) will often be obscured.
The same general problems that arise when plotting CIs in between-subjects (independent measures) ANOVA also arise for within-subjects analyses. Plotting within-subjects data also raises a more fundamental problem. In a within-subjects design, it is no longer reasonable to assume that the errors in each sample are independent. It is almost inevitable that they will be correlated—and usually positively correlated. The correlations reflect systematic individual differences that arise when measuring the same units (e.g., human participants) repeatedly. For example, participants with good memories will tend to score high on a memory task, leading to positive correlations between repeated measurements. Negative correlations might arise if repeated measurements are constrained by a common factor that forces some measurements to increase or decrease at the expense of others (e.g., a fast response time might slow down a later response if there is insufficient time to recover between them).
The main implication of this dependence is that the standard error for the differences between the means of any two samples will depend on the correlation between the two. This is evident from Eq. 3, bearing in mind that the Pearson correlation coefficient is a standardized covariance (i.e., \( {\rho_{{{X_1},{X_2}}}} = {\sigma_{{{X_1},{X_2}}}}/[{\sigma_{{{X_1}}}}{\sigma_{{{X_2}}}}] \)). Positive correlations lead to smaller standard errors, while negative correlations lead to larger standard errors. Only if the correlation between measures is close to zero would one expect the standard error of a difference in a within-subjects design to be similar to that obtained with a between-subjects design.
Within-subjects confidence intervals: some proposed solutions
Loftus–Masson intervals
In the psychological literature, the best-known solution to the problem of plotting correlated means in ANOVA designs is that of Loftus and Masson (1994; Masson & Loftus, 2003). Loftus and Masson recognized the central problem of computing within-subjects confidence intervals in the context of ANOVA. They started by noting that plotting CIs around individual means in between-subjects designs is informative about the pattern of differences between conditions (because their width is related by a factor of approximately \( \sqrt {2} \) to the width of a difference between means). In a between-subjects design, the typical approach is to use Eq. 1 to calculate the standard error from a pooled standard deviation rather than the separate estimates for each sample. This is readily derived from the between-subjects ANOVA error term, because \( {\hat{\sigma }_{{pooled}}} = \sqrt {{M{S_{{error}}}}} \). If sample sizes are equal, this will produce intervals of identical width, but when sample sizes are unequal (or if homogeneity of variance cannot be assumed) researchers are advised to compute the standard error separately for each sample. In balanced designs (those with equal cell sizes), this has the added virtue of revealing systematic patterns in the variances of the samples (e.g., increasing or decreasing width of the CI across conditions). However, because the pooled-variance estimate is based on all N observations, rather than on n within each of the J levels, the intervals with separate error terms will be slightly wider (by virtue of using \( {t_{{n - 1,1 - \alpha /2}}} \) as a multiplier rather than the value \( {t_{{N - J,1 - \alpha /2}}} \)).
Loftus and Masson (1994) proposed a method of constructing a within-subjects CI that mimics the characteristics of the usual between-subjects CI for ANOVA. In a between-subjects ANOVA, the individual differences are subsumed in the error term of the analysis, and hence reduce the sensitivity of the omnibus F test statistic (this being MS effect/MS error). Since the between-subjects CIs constructed around individual means usually use the same error term as the omnibus F test, the two procedures are broadly consistent. Clear patterns in a plot of means and CIs tend to be associated with a large F statistic. To create an equivalent plot for within-subjects CIs that is just as revealing about the pattern of means between conditions, Loftus and Masson propose constructing the CI from the pooled error term of the within-subjects F statistic. In essence, their approach is to adapt Eq. 1 by deriving \( {\hat{\sigma }_{\text{pooled}}} \) from an error term that excludes systematic individual differences.
If individual differences are large relative to other sources of error, they can have a huge impact on the width of the intervals that are plotted. Figure 1 shows data from a hypothetical free recall experiment reported by Loftus and Masson (1994), comparing three different presentation times (1, 2, or 5 s per word). The mean number of words recalled (out of 25) is plotted in Fig. 1a as if they were from a between-subjects design and in Fig. 1b as if they arose from a within-subjects design.
Data from Loftus and Masson’s (1994) hypothetical free recall experiment comparing three different presentation times (1, 2, or 5 s per word). Mean numbers of words recalled (out of 25) are plotted (a) with a conventional between-subjects CI and (b) with a within-subjects Loftus–Masson CI
Although the standard error used to construct the CI in each panel is based on MS error, this is computed from the between-subjects ANOVA as \( \sqrt {{M{S_{{within}}}/N}} \) and from the within-subjects ANOVA as \( \sqrt {{M{S_{{factor\;subjects}}}/n}} \).Footnote 3 The dramatic difference in widths in Fig. 1 is a consequence of the high correlation between repeated measurements on the same individuals (the correlations between pairs of measurements from the same individual being in the region of r = .98 for the free recall data). Real data might well produce less dramatic differences, but even the moderate correlations typical of individual differences between human participants (e.g., .20 < r < .80) are likely to have a substantial impact.
Loftus–Masson intervals are widely used, but have attracted some criticism. They correctly mimic the relationship between the default CIs and the omnibus F test found for between-subjects designs, but they necessarily assume sphericity (homogeneity of variances of the differences between pairs of repeated samples). The homogeneity-of-variances assumption is easy to avoid for between-subjects CIs by switching from pooled to separate error terms, but trickier to avoid for within-subjects CIs because the separate error terms would still be correlated. Another concern is that Loftus–Masson intervals are widely perceived as difficult to compute and plot, and this has led to several publications attempting to address these obstacles (e.g., Cousineau, 2005; Hollands & Jarmasz, 2010; Jarmasz & Hollands, 2009; Wright, 2007). A final issue is that Loftus–Masson intervals are primarily concerned with providing a graphical representation of a pattern of a set of means for informal inference. They were never intended to mimic hypothesis tests for individual means or for the differences between pairs of means. Loftus and Masson (1994; Masson & Loftus, 2003) are quite explicit about this, and it would be unreasonable to criticize their approach on this basis. However, confusion arises in practice if the Loftus–Masson approach is adopted and interpreted as a graphical implementation of a significance test.
Cousineau–Morey intervals
Cousineau (2005) proposed a simple alternative to Loftus–Masson CIs that does not assume sphericity. His approach also strips out individual differences from the calculation, but does this by normalizing the data. This procedure was also used by Loftus and Masson (1994), but only to illustrate the process of removing individual differences rather than for computing the CI. Indeed, at least one commentary on Loftus and Masson proposed constructing within-subjects CIs by normalizing the raw scores—though they refer to them as scores adjusted for between-subjects variability (Bakeman & McArthur, 1996).
The process of normalizing a data set starts by participant-mean centering: subtracting the mean of each participant from their raw scores. While this removes individual differences, it also changes the mean score for each level of the factor. Adding the grand mean back to every score restores the original means for each level. This process is illustrated in Fig. 2 for the free recall data. Panel (a) shows the spread of raw scores around each level mean. Panel (b) shows the normalized scores. The level means are indicated by a solid black line, and the grand mean by a dashed grey line. This combination of participant-mean centering followed by adding back the grand mean relocates all condition effects relative to the grand mean rather than participant means.
Figure 2 illustrates how normalized scores relate all condition effects relative to an idealized average participant (thus removing individual differences). This process could also be viewed as a form of ANCOVA in which adjusted means are calculated by stripping out the effect of a between-subjects covariate (Bakeman & McArthur, 1996). Cousineau’s (2005) proposal is to use Eq. 1 to construct CIs for the normalized samples. Because they are constructed in the same way as standard CIs for individual means, it is possible to use standard software to calculate and plot them (provided you first obtain normalized data). By removing individual differences and computing CIs from a single sample (without pooling error terms), there is also no need to assume sphericity.
Morey (2008) pointed out that Cousineau’s (2005) approach produces intervals that are consistently too narrow. Morey explains that normalizing induces a positive covariance between normalized scores within a condition, introducing bias into the estimates of the sample variances. The degree of bias is proportional to the number of means: For a one-way design with J means, a normalized variance is too small by a factor of J/(J – 1). This suggests a simple correction to the Cousineau approach, in which the width of the CI is rescaled by a factor of \( \sqrt {{\left( {J - 1} \right)/J}} \). For further discussion, and a formal derivation of the bias, see Morey’s study.
It is worth illustrating the process of constructing a Cousineau–Morey interval in a little more detail. This illustration assumes a one-way within-subjects ANOVA design with J levels. If Y ij is the score of the ith participant in condition j (for i = 1 to n), \( {\hat{\mu }_i} \) is the mean of participant i across all J levels (for j = 1 to J), and \( {\hat{\mu }_{\text{grand}}} \) is the grand mean, normalized scores can be expressed as:
The correct interval, removing the bias induced by normalizing the scores, is therefore
where \( \hat{\sigma }_{{{{\hat{\mu }}_j}}}^{\prime } \) is the standard error of the mean computed from the normalized scores of the jth level. For factorial designs, Morey indicates that J can be replaced by the total number of conditions across all repeated measures fixed factors (i.e., excluding the random factor for subjects). In practice, this involves computing the normalized scores of all repeated measures conditions as if they arose from a one-way design. If the design also incorporates between-subjects factors, the intervals can be computed separately for each of the groups defined by combinations of between-subjects factors.
The intervals themselves have the same expected width as the Loftus–Masson CIs in large samples, but do not assume sphericity. Except when J = 2, their width varies as a function of the variances and covariances of the repeated measures samples (though when J = 2, the Cousineau–Morey and Loftus–Masson intervals are necessarily identical). Because Cousineau–Morey intervals are sensitive to the variances of the samples, they are therefore potentially more informative and more robust than Loftus–Masson intervals. This comes at a small cost. By abandoning a pooled error term, the quantile used as a multiplier in Eq. 5 is \( {t_{{n - 1,1 - \alpha /2}}} \) rather than \( {t_{{\left( {n - 1} \right)\left( {J - 1} \right),1 - \alpha /2}}} \). Thus, when J > 2, the Cousineau–Morey intervals will on average be slightly wider than Loftus–Masson intervals when n is small (though any given interval could be smaller or wider, depending on the sample covariance matrix). As the aim is to produce intervals suitable for detecting patterns among means when presented graphically, this cost can be considered negligible. A possible exception is for small samples (provided also that sphericity is not seriously violated).
One further issue with the Cousineau–Morey intervals is that correcting the normalized sample variance for bias introduces an obstacle to calculating and plotting the CIs. It is no longer possible simply to apply standard software solutions to the normalized data. Cousineau (2005) provides SPSS syntax for computing the uncorrected intervals. The correction factor can be incorporated into most software by a suitable adjustment of the confidence level. For moderately large samples and J = 2, a 99% CI for the normalized scores gives an approximate 95% Cousineau–Morey interval. For instance, with α = .05 (i.e., 95% confidence) and n = 30, the usual critical value of t would be 2.045. For a factor with J = 3 levels, the correction factor is \( \sqrt {{3/2}} \approx 1.225 \). As 1.225 × 2.045 ≈ 2.5, you can mimic a 95% Cousineau–Morey interval by plotting a 98.2% CI for the normalized data using standard software. A 98.2% CI is required because t 29 = 2.5 excludes around 0.9% in each tail. It is possible to compute the required confidence level using most statistics packages or with spreadsheet software. The Appendix describes SPSS syntax for normalizing a data set and plotting Cousineau–Morey intervals.
Within-subjects intervals from a multilevel model
Blouin and Riopelle (2005) presented a critique of Loftus–Masson intervals and proposed an alternative approach based on multilevel (also termed linear mixed, hierarchical linear, or random coefficient) regression models. Multilevel models were developed to deal with clustered data such as children in schools (where children are modelled as Level 1 units nested within a random sample of schools at Level 2). Units within a cluster tend to be more similar to each other than units from different clusters. In a multilevel model, this dependency between observations is modelled by estimating the variance within and between units as separate parameters. This differs from a standard linear regression model, where a single variance parameter is estimated for the individual differences. An important advantage of multilevel regression is the ability to extend the model to deal with dependencies arising from contexts other than a simple nested hierarchy with two levels. These include hierarchies with more than two levels, or different patterns of correlations between observations within a level. A more comprehensive introduction to the topic is found in Hox (2010).
Blouin and Riopelle’s (2005) critique is quite technical and has had limited impact (perhaps because it has been presented in relation to a particular software package: SAS, SAS Institute, Cary, NC). The core of their critique is that Loftus–Masson intervals, by stripping out individual differences, derive CIs from a model in which subjects are treated as a fixed factor. In contrast, a standard CI such as those from Eqs. 1 or 2 (including the between-subjects intervals that Loftus–Masson intervals seek to mimic) treats subjects as a random effect. This implies that Loftus–Masson intervals cannot be legitimately applied for inference about individual means. This may (at first) seem like a devastating critique of the Loftus–Masson approach. However, a careful reading of Loftus and Masson (1994) reveals that this conclusion is unwarranted; as already noted, Loftus and Masson are quite careful to restrict the interpretation of their intervals to an informal, graphical inference about the pattern of means.
Blouin and Riopelle (2005) confirmed this interpretation when they reported standard errors for the Loftus and Masson (1994) free recall data (plotted here in Fig. 1) both for an individual mean and for a difference between means computed using their preferred method (a multilevel model).Footnote 4 In their example, presentation time is treated as a fixed effect, subjects are a random effect, and a covariance matrix with compound symmetry is fitted for the repeated measures (i.e., for the within-subjects effect). Under this model, the standard error for inference about an individual condition mean is 1.879, but for a difference between means it is \( \sqrt {2} \times 0.248 \). The value of 0.248 is identical to the standard error of the Loftus–Masson interval. Inference about the pattern of means (implicitly linked to the differences between pairs of means) is therefore unaffected by the choice of ANOVA or multilevel model in this instance. This should not be surprising. For balanced data, there is a well-known equivalence between a multilevel model with compound symmetry among the repeated measures and a within-subjects ANOVA model, provided that restricted maximum likelihood (RML) estimation is used to fit the multilevel model (Searle, Casella, & McCulloch, 1992). The advantage of the multilevel model—with respect to inference about a pattern of means—is therefore its flexibility (Blouin & Riopelle, 2005; Hox, 2010; Searle et al., 1992). Within the multilevel framework, it is straightforward to relax the sphericity assumption, to cope with unbalanced designs, and to incorporate additional factors or covariates.
The multilevel approach offers a flexible method for obtaining within-subjects CIs, both for revealing patterns of means and for inferences about individual means. The former are more-or-less equivalent to either Loftus–Masson or Cousineau–Morey intervals (depending on the pattern of variances and covariances being assumed). The latter are arguably superior to those constructed from individual samples (Blouin & Riopelle, 2005).
Goldstein–Healy plots
The problem of the graphical presentation of means (or indeed of other statistics such as odds ratios) occurs in contexts other than classical ANOVA designs. Goldstein and Healy (1995) proposed a simple solution designed for presenting a large collection of means. Their solution was intended to facilitate inference about differences between pairs of statistics—its best-known application being in the effectiveness of schools (e.g., by plotting estimates of Level 2 residuals for a multilevel model comparing educational attainment of children clustered within schools). The basic form of the proposal is to derive a common multiplier to the standard errors of each statistic that, when plotted, would equate to an approximate 95% CI for their difference. This multiplier combines the appropriate quantile and the requisite adjustment for a difference between independent means into a single number, thus facilitating plotting of a large number of statistics (assuming that the standard errors are available).Footnote 5
Goldstein and Healy (1995) showed that for two independent means sampled from normal distributions with known standard errors, the probability of nonoverlapping CIs with 100(1 – α) = C% confidence is given by
In this equation, \( {\sigma_{{{{\hat{\mu }}_i}}}} \) and \( {\sigma_{{{{\hat{\mu }}_j}}}} \) are the standard errors of the means, and z C is the positive quantile of the standard normal distribution z that corresponds to C% confidence. When these two standard errors are equal, the quantity \( \left( {{\sigma_{{{{\hat{\mu }}_i}}}} + {\sigma_{{{{\hat{\mu }}_j}}}}} \right)/\sqrt {{\sigma_{{{{\hat{\mu }}_i}}}^2 + \sigma_{{{{\hat{\mu }}_j}}}^2}} \) is at its maximum and γ ij is at its minimum. Conversely, γ ij is maximized when one standard error is infinitely larger than the other (e.g., \( {\sigma_{{{\mu_i}}}} = 0 \) and \( {\sigma_{{{\mu_j}}}} = 1 \)). Fixing γ ij at the desired probability and solving for z C gives the appropriate multiplier for a plot of the two means. This logic can be extended to other statistics. The quantity \( \left( {{\sigma_{{{{\hat{\mu }}_i}}}} + {\sigma_{{{{\hat{\mu }}_j}}}}} \right)/\sqrt {{\sigma_{{{{\hat{\mu }}_i}}}^2 + \sigma_{{{{\hat{\mu }}_j}}}^2}} \) can be averaged over all pairs when plotting more than two statistics (and this approach will be reasonably accurate, unless the range of standard errors is large).
A multiplier of approximately 1.39 standard errors produces approximate 95% CIs of the difference between independent statistics with equal standard errors (Goldstein & Healy, 1995). Panel (a) of Fig. 3 plots the probability of nonoverlap γ ij as a function of the right-hand side of Eq. 6. This is done separately for the smallest ratio of standard errors and for maximally different standard errors. The horizontal line at γ ij = .05 intersects these lines at 1.386 (to three decimal places) for the equal-standard-errors curve, or 1.960 if the ratio of standard errors is infinitely large (or if it approaches zero). The latter necessarily reduces to a multiplier for a single mean (the other mean being, in effect, a population parameter measured with perfect precision). The extension to the t distribution is straightforward (Afshartous & Preston, 2010; Goldstein & Healy, 1995), in which case the multiplier also varies as a function of the degrees of freedom (df). This can be seen in panels (b) and (c) of Fig. 3, where the function for nonoverlap of a CI is shown for t distributions with 9 and 29 df, respectively. The t distribution converges rapidly on z as its df become large. Thus, the z approximation is likely to be adequate, even if the standard errors are estimated from the sample standard deviation (provided that n is not very small).
Multipliers for a Goldstein–Healy plot of CIs for two independent statistics, following (a) a z distribution, (b) a t 9 distribution, and (c) a t 29 distribution. Multipliers are shown as a function of the probability of nonoverlap of their CIs and for different ratios of standard errors (equal or infinite)
For within-subjects CIs, it would be unreasonable to assume independent statistics. Afshartous and Preston (2010) consider how to construct a Goldstein–Healy plot for correlated statistics. The \( {\sigma_{{{{\hat{\mu }}_i}}}} + {\sigma_{{{{\hat{\mu }}_j}}}} \) term in Eq. 6 is derived from the variance sum law when the covariance between sample statistics is exactly zero (representing the standard error of a difference between the statistics). Expressing Eq. 3 in terms of the standard errors of the statistics and the correlation between the samples ρ ij and applying this to Eq. 6 gives the corresponding expression for within-subjects CIs,
With this equation, the average correlation between pairs of repeated measures could be used alongside the average ratio of standard errors to generate a single multiplier for a set of correlated means or other statistics. Afshartous and Preston (2010) explained how to calculate multipliers for within-subjects or between-subjects CIs using the z or t distribution. Unlike variability in standard errors or the choice of t or z, whether the statistics are independent or correlated has a huge impact on the multiplier. For instance, a modest positive correlation of ρ ij = .30 reduces the multiplier from around 1.446 to 1.210 for a t distribution with df = 29. For the same sample size, ρ ij = .75 halves the width of the CI in relation to the independent case (from 1.446 to 0.7231).
A Goldstein–Healy plot provides a quick and easy way to generate a standard error multiplier for plotting between-subjects or within-subjects CIs (and the approach is exact if only two means are plotted). One crucial difference with the Loftus–Masson and Cousineau–Morey intervals is that intervals are designed so that lack of overlap between 95% intervals corresponds to a 95% CI for the difference that does not include zero (i.e., to a null-hypothesis significance test of the difference between statistics at α = .05). Thus, on average, the width of a CI for the Goldstein–Healy plot is smaller than that of a standard Loftus–Masson or Cousineau–Morey interval.
Selecting the correct interval to plot
In selecting the correct interval to plot, it is first necessary to consider the inferences they support. Graphical presentation of interval estimates is best suited to informal inference. Nevertheless, it is helpful to pick a method that generates intervals that are at least roughly equivalent to a CI used for formal inference. The principal reason for this is that people (including some experienced researchers) often interpret overlapping 95% CIs as equivalent to a nonsignificant difference between statistics (Belia, Fidler, Williams, & Cumming, 2005). This will not always be true, depending on the type of inference being made and the choice of interval that is plotted (Cumming & Finch, 2005; Schenker & Gentleman, 2001). The problem can be avoided by applying rules of thumb (e.g., 50% overlap corresponds to a significant difference), but it would be preferable to plot an interval corresponding to the inference of primary interest and thus to avoid the problem altogether (Goldstein & Healy, 1995; Moses, 1987).Footnote 6
The methods for constructing within-subjects CIs discussed in the previous section can be grouped roughly into three broad approaches. First, the Loftus–Masson and Cousineau–Morey intervals aim to reveal a pattern among means consistent with an omnibus F test in ANOVA. Second, the Goldstein–Healy plot aims to depict intervals for which lack of overlap roughly corresponds to a significant difference between statistics. Third, a multilevel model can provide intervals for the individual means that treat subjects as a random factor. A further distinction is that the Goldstein–Healy plot and Loftus–Masson intervals make fairly strong assumptions about the form of the covariance matrix (either by using a pooled error term or by assuming a common correlation between conditions). Cousineau–Morey intervals assume neither sphericity nor homogeneity of covariances (and are also fairly easy to compute). A multilevel model is the most flexible approach, and either compound symmetry or an unstructured covariance matrix (or covariance structures of intermediate complexity) can be adopted. This leads naturally to a choice of intervals that depends on the primary inference of interest and the nature of the correlation structure between repeated measures in the population.
It is possible to narrow down the choice of intervals by realizing that there is a clear link between the Loftus–Masson and Goldstein–Healy approaches. Both broadly address the same question—but by slightly different routes. Assuming large samples with equal variances and covariances, the expected width of both Loftus–Masson and Cousineau–Morey intervals is larger than that of the interval in a Goldstein–Healy plot by the familiar factor of \( \sqrt {2} \). It is therefore simple to adjust either interval to match the other. Because the Cousineau–Morey intervals assume neither sphericity nor homogeneity of covariances for the repeated measures they should, as a rule, be preferred over the other two methods. Sphericity only infrequently holds for real data sets (with the exception of within-subjects ANOVA effects with 1 df in the numerator—equivalent to a paired t test—for which sphericity is always true). Because violations of sphericity always lead to inferences that are too liberal (e.g., CIs that are too narrow), it makes sense to choose interval estimates that relax the assumption by default.
For inferences about differences in means that are consistent with the omnibus F test from within-subjects ANOVA, and for which nonoverlap of CIs corresponds to an inference of no difference, I propose plotting Cousineau–Morey intervals with the following adjustment:
The \( \sqrt {2} /2 \) factor adjusts a Loftus–Masson or Cousineau–Morey interval to match that of a CI for a difference (see, e.g., Hollands & Jarmasz, 2010). This equation combines advantages of computing a standard error from normalized data with the ease of interpretation of CIs in a Goldstein–Healy plot.
It is worth making the reasoning behind the \( \sqrt {2} /2 \) adjustment factor explicit. Although the ratio of the width of the CI for a difference to the CI for an individual mean is \( \sqrt {2} \) to 1, this must be halved when plotting intervals around individual means. For a difference in means, inference depends on the margin of error around one statistic including or not including a parameter value (e.g., zero). Lack of overlap of CIs plotted around individual means depends on the margin of error around two statistics. To ensure that the sum of the margin of error around each statistic is \( \sqrt {2} \) times larger than for an individual statistic, it is necessary to scale each individual margin of error (w) by the \( \sqrt {2} /2 \) factor (i.e., \( \sqrt {2} /2w + \sqrt {2} /2w = \sqrt {2} w \)). The halving is therefore a trivial, but easily overlooked, consequence of plotting two intervals rather than one.
In some cases, it may be reasonable to plot an adjusted Loftus–Masson interval instead. For a one-way within-subjects ANOVA, this takes the form
where MS error is the denominator of F statistic for the test of the factor. When sphericity holds, Eq. 9 offers a modest advantage over Eq. 8 when n – 1 is small (e.g., below 15) and (n – 1)(J – 1) is large (e.g., over 30). Note that Eq. 9 also explains the correspondence between the Goldstein–Healy plot and adjusted Loftus–Masson intervals. The multiplier in the former combines the \( {{{\sqrt {2} }} \left/ {2} \right.} \) adjustment and the quantile \( {t_{{\left( {n - 1} \right)\left( {J - 1} \right),1 - \alpha /2}}} \) in the latter (\( \sqrt {{M{S_{{error}}}/n}} \) being the standard error). One further distinction is that the Loftus–Masson intervals deal with within-subjects designs by removing individual differences from the standard error. The spirit of the Goldstein–Healy plot is to adjust only the multiplier, and thus Afshartous and Preston (2010) recalculate the multiplier of the Goldstein–Healy plot to take account of the correlation between the standard errors.
For many applications of ANOVA, it is sufficient to focus on the pattern of means and differences between pairs of means. In this case, the adjusted Cousineau–Morey interval proposed here is a sensible candidate. In some applications of ANOVA, the primary focus will be on inference about individual means. This might arise in a longitudinal study where the focus is on whether the mean is different from some threshold at each time point. If so, it would be more appropriate to plot CIs derived from a multilevel model. One of the advantages of this approach is the ability to relax the sphericity assumption by fitting a model with an unstructured covariance matrix (estimating the variances and covariances between repeated measures with separate parameters).
I have suggested that inference about individual means is only infrequently the main focus of inference for ANOVA designs. Nevertheless, there will almost always be some interest in the width of the CI for the individual means. For example, in a recognition memory experiment, the main focus will usually be on differences between conditions, but it would also be valuable to ascertain whether performance in each condition exceeds chance. The width of a CI for an individual mean also indicates the precision with which that statistic has been measured (Kelley, Maxwell, & Rausch, 2003; Loftus, 2001). For this reason alone, it would be advantageous to be able to display CIs representing differences between means alongside those depicting the precision with which each sample is measured. Simultaneous plotting of two distinct interval estimates can be addressed in several ways, but perhaps the most elegant and user-friendly display is a two-tiered CI: a form of two-tiered error bar plot (Cleveland, 1985).
The outer tier of a two-tiered CI is plotted as a standard error bar. The inner tier is then formed by drawing a line at right angles to the error bar with the required margin of error (as if shifting the line commonly drawn at the limits of the interval so that it bisects the error bar). Cleveland (1985) used the inner tier of the error bar to designate a 50% CI (similar to the central box of a box plot), while the outer tier represented a 95% CI for each statistic. I propose using the outer tier to depict a 95% CI for an individual mean and drawing the inner tier so that lack of overlap corresponds to a 95% CI for the difference in means. This property is demonstrated in Fig. 4, in which two-tiered CIs for the difference between two correlated means are displayed.
Overlap of the inner-tier error bars of a two-tiered 95% CI corresponds to statistical significance with α = .05 and indicates that the 95% CI for a difference includes zero. In panel (a), there is clear separation of the inner-tier error bars, and the paired t test is statistically significant (p < .05). In panel (b), the inner-tier error bars are adjacent, and the paired t test is on the cusp of statistical significance (p = .05). In panel (c), the inner-tier error bars show substantial overlap, and the paired t test does not reach statistical significance (p > .05)
In panel (a), the correlation between paired observations is substantial (r = .8) and a paired t test is statistically significant (p = .001). In panel (b), the correlation between paired observations is lower (r = .6) and the paired t test is on the cusp of statistical significance (p = .05). In panel (c), the correlation between paired observations is lower still (r = .45) and the paired t test is nonsignificant (p = .10). Figure 4 demonstrates the close correspondence between overlap of the inner error bars and statistical significance from a paired t test (and, by implication, a CI for a difference that includes zero as a plausible value).
Figure 5 depicts two-tiered CIs for the free recall data constructed in this way. Panel (a) plots 95% CIs from a multilevel model with an unstructured covariance matrix for the outer tier and difference-adjusted Cousineau–Morey intervals for the inner tier. Panel (b) plots 95% CIs from a multilevel model under the assumption of compound symmetry for the repeated measures as the outer tier and difference-adjusted Loftus–Masson intervals for the inner tier.
Two-tiered CIs for the free recall data. In panel (a), the outer tier is a 95% CI derived from a multilevel model with an unstructured covariance matrix, while the inner tier is a difference-adjusted Cousineau–Morey interval. In panel (b), the outer tier is a 95% CI derived from a multilevel model with a covariance matrix constrained to compound symmetry, while the inner tier is a difference-adjusted Loftus–Masson interval
For these data, the correlations between repeated measures are both very high and very consistent. It follows that both constrained and unconstrained covariance matrix approaches will produce similar results. This is the case even though n = 10 (which implies that the Loftus–Masson intervals are on average slightly narrower than the Cousineau–Morey intervals).Footnote 7 Looking at the two-tiered CI, the presence of plausible differences between the conditions—indicated by nonoverlapping inner error bars—is obvious. Also obvious is the lack of precision with which individual means are measured. So while the experiment provides clear evidence of differences between conditions, it is also clear that participants vary considerably on this task and that each population mean is estimated very imprecisely.
The recipe for construction of a two-tiered CI described here is suitable when—as is common—the correlation between the samples is positive. If some covariances are negative or if sample sizes are very small, the recipe could fail: The (outer) multilevel CI may be narrower than the (inner) difference-adjusted CI. When n for one or more samples is very low (e.g., <10), the quality of the variance and covariance estimates is likely to be poor. A pooled error term is likely to provide superior estimates in this situation (particularly if negative correlations have arisen through sampling error). In larger samples, any negative correlations are likely to reflect a process of genuine interest to a researcher, and it may be better to plot the individual means and differences separately (even if adopting a pooled error term produces a “successful” two-tiered CI plot).Footnote 8
Constructing one-tiered and two-tiered confidence interval plots
Cousineau–Morey CIs can be computed from standard ANOVA output without too much difficulty (e.g., using spreadsheet software such as Excel). Single-tier CI plots can be generated with a little more effort. Many statistical packages, such SPSS, also have options to fit multilevel models for within-subjects ANOVA designs and can provide appropriate CIs for individual means. Constructing a two-tier plot is more difficult. To facilitate this process for one-tier plots and to support the use of two-tiered plots, it is possible to write custom macros or functions. This section introduces R functions for computing and plotting one-tiered and two-tiered plots for Loftus–Masson, Cousineau–Morey, and multilevel model intervals (R Development Core Team, 2009). I provide the code for new R functions to compute the CIs and construct the plots in the supplementary materials for this article. Other functions used here are loaded automatically with R or are part of the R base installation. Their application is illustrated first for a one-way within-subjects design. For the Cousineau–Morey and multilevel model approaches, it is also extended to deal with two-way mixed designs. R was chosen because it is free, open source, and runs on Mac, Windows, and Linux operating systems. This removes a further obstacle preventing researchers from graphical presentation of means from within-subjects ANOVA designs. Goldstein–Healy plots, more suited to large collections of means and other statistics, are not implemented. However, Afshartous and Preston (2010) have provided R functions for calculating multipliers for between-subjects (independent) and within-subjects (dependent) designs for both z and t distributions.
Confidence intervals for one-factor ANOVA designs
The following examples use the free recall data from Loftus and Masson (1994). This data set and the emotion data set used in later examples are included in the supplementary materials. The first step is to load the data into R. Two options are illustrated here. The first assumes that the data set is in the form of a comma-separated variable (.csv) file. The second assumes that data are in an SPSS (.sav) data file. R functions usually take within-subjects (repeated measures) data in long form, with each observation on a separate row, but most ANOVA software requires the data in broad form (where each person is on a separate row).Footnote 9 Data imported from other software will therefore usually arrive in broad format. For this reason, the R functions described here take input as a data frame (effectively a collection of named variables arranged in columns) in broad form. The file  is arranged in three columns so that the first row contains the three condition names (
is arranged in three columns so that the first row contains the three condition names ( ,
,  and
and  ) and the next 10 rows contain the raw data. To import data from this file, type
) and the next 10 rows contain the raw data. To import data from this file, type  at the R console prompt and then hit the return key.Footnote 10 R will import the data into the data frame
at the R console prompt and then hit the return key.Footnote 10 R will import the data into the data frame  and use the header row as column names. If the data are in an SPSS .sav file, it is first necessary load the
and use the header row as column names. If the data are in an SPSS .sav file, it is first necessary load the  package (a part of the base installation that allows for importing of data from other packages). The following commands use the
package (a part of the base installation that allows for importing of data from other packages). The following commands use the  function to import the data:
function to import the data:

The additional  argument overrides the default behaviour of the function (which is to import data as an R list object).
argument overrides the default behaviour of the function (which is to import data as an R list object).
For one-way ANOVA, the functions  and
and  provide between-subjects, Loftus–Masson, and Cousineau–Morey intervals, respectively.Footnote 11 Each is structured in the format
provide between-subjects, Loftus–Masson, and Cousineau–Morey intervals, respectively.Footnote 11 Each is structured in the format 
 . The first argument is the name of the R data frame object containing the data in broad format (and must be included). The second argument is the desired confidence level, and defaults to .95 (95%) if omitted. The third argument takes the value
. The first argument is the name of the R data frame object containing the data in broad format (and must be included). The second argument is the desired confidence level, and defaults to .95 (95%) if omitted. The third argument takes the value  or
or  and indicates whether to adjust the width of the interval so that absence of overlap of CIs for two means corresponds to a 95% CI for their difference. It defaults to
and indicates whether to adjust the width of the interval so that absence of overlap of CIs for two means corresponds to a 95% CI for their difference. It defaults to  for
for  and
and  , and
, and  for
for  . To call each function with its default settings, use the format
. To call each function with its default settings, use the format  . For example, difference-adjusted 95% Cousineau–Morey intervals for the free recall data are obtained from the call:
. For example, difference-adjusted 95% Cousineau–Morey intervals for the free recall data are obtained from the call:  . The output takes the form
. The output takes the form

It is easy to override the defaults. The following calls generate 99% Cousineau–Morey intervals or difference-adjusted 95% between-subjects intervals:

These functions require data structured in the appropriate way. If the data frame is in broad form but also includes columns that are not relevant to the analysis, the required variables can be selected by column number. For example, if only the 2-second and 5-second conditions are of interest, the following call, selecting only Columns 2 and 3, is appropriate:

Multilevel models can be run using several different packages in R. Here, I use the  package. This is also part of the base R installation (Pinheiro, Bates, DebRoy, Sarkar, & R Core Team, 2009). In addition, the
package. This is also part of the base R installation (Pinheiro, Bates, DebRoy, Sarkar, & R Core Team, 2009). In addition, the  package is used to compute the interval estimates (Warnes et al., 2009). The
package is used to compute the interval estimates (Warnes et al., 2009). The  package is not part of the base installation and needs to be installed.Footnote 12 Both packages are loaded and later detached each time the function is run. This approach is slightly inefficient but makes it less likely that the function will interfere with other packages the user is working with. The multilevel function described here has the format
package is not part of the base installation and needs to be installed.Footnote 12 Both packages are loaded and later detached each time the function is run. This approach is slightly inefficient but makes it less likely that the function will interfere with other packages the user is working with. The multilevel function described here has the format  . The third argument has the default
. The third argument has the default  and specifies the type of covariance matrix fitted for the repeated measures. To fit a model that assumes compound symmetry, use the argument
and specifies the type of covariance matrix fitted for the repeated measures. To fit a model that assumes compound symmetry, use the argument  . The following calls produce 95% CIs for the free recall data with each of the two covariance structure options:
. The following calls produce 95% CIs for the free recall data with each of the two covariance structure options:

One-tiered and two-tiered confidence interval plots for one-way designs
The CIs obtained from these functions can be used for plotting within R, or as input for other software that has suitable options for specifying a plot. The  function described here will plot single-tiered CIs using any of the functions above. The choice of interval is described by the
function described here will plot single-tiered CIs using any of the functions above. The choice of interval is described by the  argument, with the default being
argument, with the default being  (Cousineau–Morey intervals), and other options being
(Cousineau–Morey intervals), and other options being  (Loftus–Masson),
(Loftus–Masson),  (between subjects), and
(between subjects), and  (multilevel). For the first three types, the
(multilevel). For the first three types, the  argument defaults to
argument defaults to  (but is ignored if
(but is ignored if  ). For
). For  , the
, the  argument defaults to
argument defaults to  (and is ignored for any other type of interval). Additional arguments alter elements of the plot such as axis labels, limits of the y-axis, main title, error bar line widths, or the point symbol. Further adjustments are possible by editing the plot or altering the plot parameters in R. The following commands reproduce panels (a) and (b) of Fig. 1:
(and is ignored for any other type of interval). Additional arguments alter elements of the plot such as axis labels, limits of the y-axis, main title, error bar line widths, or the point symbol. Further adjustments are possible by editing the plot or altering the plot parameters in R. The following commands reproduce panels (a) and (b) of Fig. 1:

The default behaviour of the function is to produce the option recommended here: a Cousineau–Morey CI with an adjustment, so that nonoverlapping intervals correspond to the 95% CI for their difference. Thus, the following two calls are equivalent:

The composition of a tiered plot is less flexible. It makes sense to pair multilevel-model CIs with an unstructured covariance matrix to Cousineau–Morey intervals. Likewise, it makes sense to pair a multilevel-model CI that assumes compound symmetry to Loftus–Masson intervals. The interval type is determined by the  argument. The former is the default output (
argument. The former is the default output ( ), while the latter requires the argument
), while the latter requires the argument  . The
. The  argument influences only the inner tier and adjusts either the Cousineau–Morey or Loftus–Masson intervals by the \( \sqrt {2} /2 \) factor required to support inferences about differences between means. As before, this is set by the argument
argument influences only the inner tier and adjusts either the Cousineau–Morey or Loftus–Masson intervals by the \( \sqrt {2} /2 \) factor required to support inferences about differences between means. As before, this is set by the argument  (which is the default).
(which is the default).
As for the  function, additional arguments can be supplied to influence the look of the plot or alter titles and labels. The
function, additional arguments can be supplied to influence the look of the plot or alter titles and labels. The  function also takes three further arguments:
function also takes three further arguments:  for the size of the points being plotted,
for the size of the points being plotted,  for the size of text labels, and
for the size of text labels, and  or
or  (to add a grid to the plot). The grid is particularly useful for a complex two-tiered plot, where the grid can make it easier to detect overlap. Thus panels (a) and panel (b) of Fig. 5 can be reproduced with the following R code:
(to add a grid to the plot). The grid is particularly useful for a complex two-tiered plot, where the grid can make it easier to detect overlap. Thus panels (a) and panel (b) of Fig. 5 can be reproduced with the following R code:

A basic two-tiered plot (with Cousineau–Morey intervals for differences between means as the inner tier and multilevel CIs with an unstructured covariance matrix as the outer tier) is therefore obtained by:

To augment the display, plotting parameters can be edited using the  function, and lines or other features added to the plot using
function, and lines or other features added to the plot using  , or one of many other R graphics functions.Footnote 13 Hence, to add dashed lines (line type
, or one of many other R graphics functions.Footnote 13 Hence, to add dashed lines (line type  ) connecting the level means to the free recall plot, either of these functions will work:
) connecting the level means to the free recall plot, either of these functions will work:

Functions for two-way mixed ANOVA designs
Obtaining intervals for more complex designs using the Cousineau–Morey or multilevel approaches is not too difficult in R. The principal obstacle is to rewrite the functions to pick out a grouping variable from a data frame in broad format. Deciding how to plot the intervals is more challenging. The functions in this section demonstrate one solution to plotting the intervals. This is implemented for the two-tiered plot only.
The functions take input in the form of a data frame in which some columns represent the J levels of the within-subjects factor, and either the first or last column is the grouping variable for the between-subjects factor (with the last column being designated by default). The following example uses data from an experiment looking at recognition of emotions from facial expression and body posture in young children.Footnote 14 Three groups of children were shown photographs of actors displaying the emotions pride, happiness, or surprise. Members of one group were shown pictures of both face and torso, members of a second group were shown torso alone, and children in a third group were shown face alone. These data are contained in the file  . To load these into R (as a data frame), use the following command:
. To load these into R (as a data frame), use the following command:

To view the data, type the name of the data frame ( ) and hit the return key. For longer files, you may wish to use the
) and hit the return key. For longer files, you may wish to use the  function to see just the first few rows. The groups are coded numerically from 1 (both face and torso), through 2 (torso alone), to 3 (face alone).Footnote 15 The functions
function to see just the first few rows. The groups are coded numerically from 1 (both face and torso), through 2 (torso alone), to 3 (face alone).Footnote 15 The functions  and
and  are similar to those described earlier, except that they each take an additional argument:
are similar to those described earlier, except that they each take an additional argument:  . This indicates the column containing the grouping variable. It may take only the value
. This indicates the column containing the grouping variable. It may take only the value  or
or  (with
(with  being the default). Because the grouping variable is in the first column of the
being the default). Because the grouping variable is in the first column of the  data frame, the following calls are required to produce Cousineau–Morey intervals (adjusted for differences between means) and multilevel CIs for individual means (with an unstructured covariance matrix).
data frame, the following calls are required to produce Cousineau–Morey intervals (adjusted for differences between means) and multilevel CIs for individual means (with an unstructured covariance matrix).

The options for the structure of the multilevel covariance matrix deserve further discussion. Mixed ANOVA designs (those with both between-subjects and within-subjects factors) fit a model that assumes multisample sphericity (Keselman, Algina, & Kowalchuk, 2001). This requires that the covariance matrices for each of the groups be identical in the population being sampled. This is unlikely to hold in practice. Accordingly, the safest option is to fit a model in which the covariances between repeated measurements are free to vary, and in which groups are independent (but not constrained to be equal). This option is selected by default, or via the  argument, though a simpler structure will sometimes suffice. This argument supports two other options. The
argument, though a simpler structure will sometimes suffice. This argument supports two other options. The  argument fits a matrix with compound symmetry within each group (though neither variances nor covariances between groups are constrained to be equal). The final option is multisample compound symmetry (
argument fits a matrix with compound symmetry within each group (though neither variances nor covariances between groups are constrained to be equal). The final option is multisample compound symmetry ( ), in which all groups share a common variance and the covariances within and between groups are equal.
), in which all groups share a common variance and the covariances within and between groups are equal.
To produce two-tiered CI plots using these functions, use the  function. This will plot Cousineau–Morey intervals as the inner tier and CIs from a multilevel model as the outer tier. By default, it adjusts the inner tier to correspond to a difference between means, while the outer tier assumes an unstructured covariance matrix. Simpler covariance structures can be fitted if necessary. Even with moderate-sized data sets, fitting an unstructured covariance matrix for a two-way design could take some time (e.g., it takes up to a minute for the emotion data using a reasonably powerful desktop computer). For this reason, it may be convenient to set up a plot using a simple covariance structure (e.g., adjusting the plot parameters as desired) and switch to the unstructured covariance matrix as a final step. A two-tiered plot for the emotion data set can be fitted with each of the three available covariance structures as follows:
function. This will plot Cousineau–Morey intervals as the inner tier and CIs from a multilevel model as the outer tier. By default, it adjusts the inner tier to correspond to a difference between means, while the outer tier assumes an unstructured covariance matrix. Simpler covariance structures can be fitted if necessary. Even with moderate-sized data sets, fitting an unstructured covariance matrix for a two-way design could take some time (e.g., it takes up to a minute for the emotion data using a reasonably powerful desktop computer). For this reason, it may be convenient to set up a plot using a simple covariance structure (e.g., adjusting the plot parameters as desired) and switch to the unstructured covariance matrix as a final step. A two-tiered plot for the emotion data set can be fitted with each of the three available covariance structures as follows:

The plot can be customized (e.g., adding or editing labels and other features). Particularly important for a mixed ANOVA is the ability to change the colour, size, and type of point symbol for each group. Arguments to alter these features and also to add lines connecting groups are incorporated in the function. The  argument displaces points from the same group along the x-axis to reduce clutter. Its default value depends on the number of groups but can be increased or reduced. Some examples follow:
argument displaces points from the same group along the x-axis to reduce clutter. Its default value depends on the number of groups but can be increased or reduced. Some examples follow:

Figure 6 shows a two-tiered plot for the emotion data.
Two-tiered plot for a two-way mixed ANOVA design using the emotion data. The groups (both face and torso, torso alone, or face alone) are identified by different plot and line symbols, while the within-subjects factor (emotion) is identified on the x-axis. The outer tier of the error bars depicts a 95% CI for an individual mean derived from a multilevel model with an unstructured covariance matrix, while the inner tier is a difference-adjusted Cousineau–Morey interval
The R code to reproduce this plot is:

A two-way ANOVA on the emotion data reports a statistically significant emotion by group interaction (F 4,174 = 8.34) that the plot can help to interpret. The dark grey horizontal line at 33.3% in Fig. 6 represents recognition performance expected by random guessing (since there were three options for each picture) and was added with the call:

The pattern in Fig. 6 is not a simple one, but the inner-tier CIs suggest that accuracy is generally high and at similar levels, except for two means (where performance is markedly lower). These are for recognizing pride by face alone and happiness by torso alone. This suggests that children recognize pride mainly by body posture and happiness through facial expression. The outer-tier intervals are generally comfortably above chance levels (being above the grey line). However, for recognizing happiness from body posture alone, children are performing at levels consistent with chance. Recognizing pride from facial expression is also not much different from chance (and the outer-tier CI just overlaps the grey line).
Conclusions
Graphical presentation of means for within-subjects ANOVA designs has long been recognized as a problem, with several possible solutions having been proposed (e.g., Afshartous & Preston, 2010; Blouin & Riopelle, 2005; Loftus & Masson, 1994; Morey, 2008). The recommended solutions reviewed earlier are summarized in Table 1.
The approach advocated here is to use Eq. 8 to plot difference-adjusted Cousineau–Morey intervals: intervals calibrated so that an absence of overlap corresponds to a CI for a difference between two means. This solution avoids the restrictive assumption of sphericity and matches the inference of primary interest for most ANOVA analyses: patterns among a set of condition means. Each of the solutions summarized in Table 1 could, in principle, be used to implement formal inference for the parameter of interest. This should generally be avoided, because there are limitations to the approach with respect to formal inference (where issues such as corrections for multiple comparisons come to the fore). These and other limitations are considered in more detail below.
Sometimes interest focuses on whether individual means are different from some population value (e.g., chance performance). In this case, and following Blouin and Riopelle (2005), a multilevel model can be used to derive the appropriate interval estimates (and models can be fitted that relax the sphericity assumption or cope with imbalance). In many cases, both types of inference are of interest, and two-tiered CIs can be plotted. In a two-tiered plot, the outer tier depicts the CI for an individual mean and the inner tier supports inferences about differences between means. For plotting large numbers of means or other statistics, a Goldstein–Healy plot is a convenient alternative (Afshartous & Preston, 2010; Goldstein & Healy, 1995).
A practical obstacle to graphical presentation of means is that few of the options are implemented in widely available statistics software. I have provided R functions that compute CIs and generate both one-tiered and two-tiered plots for the Loftus–Masson, Cousineau–Morey, and multilevel approaches reviewed here. The initial focus is on intervals for a one-way ANOVA design, but it is possible to modify these functions for more complex designs (and this is illustrated for a two-way mixed ANOVA).
Potential limitations
There are several potential limitations of the approach advocated here. First, emphasis is on informal inference about means or patterns of means. The interval estimates proposed here will be reasonably accurate for most within-subjects ANOVA designs, but are intended chiefly as an aid to the exploration and interpretation of data. Thus, they may compliment formal inference, but are not intended to mimic null-hypothesis significance tests.
Even so, informal inference is more than sufficient to resolve many research questions—notably where the effects are very salient in a graphical display. This suggests that formal inference should be reserved to test hypotheses that relate to patterns that are not easily detected by eye, or to quantify the degree of support for a particularly important hypothesis. In the context of ANOVA, such hypotheses are not typically addressed by the omnibus test of an effect, but by focused contrasts (see, e.g., Loftus, 2001; Rosenthal, Rosnow, & Rubin, 2000).Footnote 16 Furthermore, formal inference need not take the form of a null-hypothesis significance test. Rouder, Speckman, Sun, Morey, and Iverson (2009) recommend CIs for reporting data but advocate Bayes factors for formal inference. Dienes (2008) describes approaches for Bayesian and likelihood-based inference for contrasts among means and provides MATLAB code to implement them.Footnote 17 Contrasts are particularly useful for testing hypotheses about complex interaction effects (Abelson & Prentice, 1997). Thus, the limitations of graphical methods for inference may, paradoxically, be an advantage. As noted in the introduction, significance tests tend to be overused, and those tests not relating to the main hypotheses of interest can often be replaced by a graph with appropriate interval estimates. Formal inference can then be reserved for tests of a small number of important hypotheses.
A second limitation is that all of the approaches discussed here make distributional assumptions that may not hold in practice. Where the errors of the statistical model are not at least approximately normal—and particularly where they follow heavy-tailed or highly skewed distributions—interval estimates based on the z or t distribution may not provide good approximations (see, e.g., Afshartous & Preston, 2010). For the Loftus–Masson and Cousineau–Morey approaches, it is possible to apply bootstrap solutions. Wright (2007) provides R functions for bootstrap versions of the Loftus–Masson intervals for one-way ANOVA. For more complex designs, it is advisable to apply a bespoke solution. The best approach may be to bootstrap trimmed means or medians (rather than means), and the adequacy of the bootstrap simulations in each case needs to be checked (see Wilcox & Keselman, 2003). Similar reservations arise for complex multilevel models. However, the equivalence of multilevel models with balanced designs to within-subjects ANOVA models (at least when restricted maximum likelihood estimation is used and compound symmetry assumed) suggests that CIs will be sufficiently accurate for the range of models implemented here. This may no longer be true for very unbalanced designs or where the distributional assumptions of ANOVA are severely violated. One alternative is to obtain the highest posterior density (HPD) intervals from Markov chain Monte Carlo simulations (see, e.g., Baayen, Davidson, & Bates, 2008). In addition, if bootstrapping or other approaches are required for the CIs, the conventional ANOVA model may be unsuitable, and other approaches should be considered. In short, if a within-subjects ANOVA is considered suitable in the first place, the proposed solutions implemented here should suffice for informal inference.
The final limitation is that I have not explicitly considered the issue of multiple testing. Correcting for multiple testing is a difficult problem for informal inference. As a large number of inferences can be drawn, and as different people will be interested in different questions, it may not be appropriate to determine any correction in advance. For graphical presentation of means, it is more appropriate to report uncorrected CIs and take account of multiple testing in other ways. For example, with J = 5 means, there are \( J\left( {J - 1} \right)/2 = 10 \) possible pairwise comparisons. This implies that one pair of appropriately adjusted 95% CIs would be expected not to overlap just by chance. Where the number of inferences to be drawn is known in advance, it is possible to make a Bonferroni-style correction by altering the confidence level (e.g., for five tests, a 99% CI is a Bonferroni-adjusted 95% CI). The drawback of this approach is that corrections for multiple testing suitable for plotting tend to be very conservative. If multiple corrections are critical, it is best to supplement graphical presentation with formal a priori or post hoc inference using a procedure that also controls Type I error rates in a strong fashion.Footnote 18 There are also more formal treatments of the multiple-comparison problem in relation to a Goldstein–Healy plot (see Afshartous & Preston, 2010; Afshartous & Wolf, 2007).
Summary
It is possible to offer a solution to plotting within-subjects CIs that is both accurate and robust to violations of sphericity. The intervals themselves can be calculated and plotted in R with the functions provided here. These interval estimates are suitable for exploratory analyses and informal inference when reporting data from classical ANOVA designs, and they are designed to support graphical inference about the pattern of means across conditions. When both types of inference are of interest, they can be displayed together as a two-tiered CI.
Notes
Alternatives exist that relax some or all of these assumptions, but are not relevant to the present discussion.
Visual display of interval estimates lends itself to the informal interpretation of a CI favoured here. CIs can also be used for formal inference, and if so, the same problems arise.
In a one-way design, MS within is a pooled variance that can be computed directly as the average of the variances of the groups. MS factor×subjects is also a pooled variance, but one equivalent to averaging the variances of the differences between correlated samples.
Blouin and Riopelle (2005) frame the distinction in terms of the SAS terminology “broad” or “narrow” inference spaces. However, in this case, the distinction (which is more general) boils down to inference about means or differences in means. I assume most readers are unfamiliar with SAS terminology and attempt a simpler exposition.
A plot involving such a large number of statistics is sometimes termed a caterpillar plot—for its resemblance to the insect. The term Goldstein–Healy plot is preferred here (because the focus is on plotting intervals for a small number of means for which the resemblance is typically lost).
Moses (1987) advocated plots with a multiplier of 1.5 standard errors for independent statistics (a variant of a Goldstein–Healy plot that tends to be slightly conservative).
In moderate to large samples, true coverage for the two intervals should be very similar when sphericity is true (and close to nominal coverage for samples from populations with normal errors), but for even quite modest violations of sphericity, the coverage of Loftus–Masson intervals is likely to unacceptable (see Mitzel & Games, 1981).
In most cases where the “inner” tier error bars fall outside the range of the “outer” tier, the bars fall close to the ends of the vertical line representing the multilevel CI and appear coherently “grouped.” This unusual variant of the two-tiered plot is still interpretable (and can act as a diagnostic for the presence of negatively correlated samples). R code illustrating such a plot is included in the supplementary materials published with this article.
Switching between long and broad forms can be accomplished using the
 function in R. SPSS users can restructure the data set using the
function in R. SPSS users can restructure the data set using the  command.
command.R will import files from its working directory. If the data are not in this directory, either change the working directory or specify the full path name (not illustrated here because it depends on the operating system).
The between-subjects CI function is implemented primarily for purposes of comparison. It uses a pooled variance estimate and also only takes input in broad format (rather than the usual long format).
The call
 will download and install the package from an online repository (and you may be prompted to select one if you have not previously installed a new package).
will download and install the package from an online repository (and you may be prompted to select one if you have not previously installed a new package).To find out more about any function in the R base installation, use the
 function or
function or  . The call
. The call  or
or  brings up information about the graphical parameters.
brings up information about the graphical parameters.These data are from an unpublished study by Uppal (2006).
If the groups are coded with text labels, R will treat the codes as a factor object and arrange the levels in alphabetical order by default. Using numeric codes makes it easier to reorder the groups.
Any ANOVA contrast can be viewed as a difference between two means (constructed from weighted linear combinations of a set of sample means). It is therefore relatively straightforward to plot a CI for a contrast using conventional methods (though it is generally more helpful to plot the set of unweighted means, as advocated here). If a plot of the contrast itself is required, it is probably better to plot a CI of the weighted difference itself rather than plot the weighted means separately. In addition, it is important to rescale the contrast weights so that their absolute sum is 2, or else the difference will no longer be on the same scale as the original means (see Kirk, 1995, p. 114).
For R code, see Baguley and Kaye (2010).
Multiple testing can also be addressed by switching to Bayesian or likelihood-based methods. However, there is some disagreement about whether multiple testing is a problem outside of frequentist statistics (for a brief discussion, see Dienes, 2008).
References
Abelson, R. P. (1995). Statistics as principled argument. Hillsdale: Erlbaum.
Abelson, R. P., & Prentice, D. A. (1997). Contrast tests of interaction hypotheses. Psychological Methods, 2, 315–328.
Afshartous, D., & Preston, R. A. (2010). Confidence intervals for dependent data: Equating nonoverlap with statistical significance. Computational Statistics and Data Analysis, 54, 2296–2305.
Afshartous, D., & Wolf, M. (2007). Avoiding data snooping in multilevel and mixed effects models. Journal of the Royal Statistical Society: Series A, 170, 1035–1059.
American Psychological Association. (2010). Publication manual of the American Psychological Association (6th ed.). Washington: Author.
Baayen, R. H., Davidson, D. J., & Bates, D. M. (2008). Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language, 59, 390–412.
Baguley, T. (2009). Standardized or simple effect size: What should be reported? British Journal of Psychology, 100, 603–617.
Baguley, T., & Kaye, W. S. (2010). Review of Understanding psychology as a science: An introduction to scientific and statistical inference. British Journal of Mathematical and Statistical Psychology, 63, 695–698.
Bakeman, R., & McArthur, D. (1996). Picturing repeated measures: Comments on Loftus, Morrison, and others. Behavior Research Methods, Instruments, & Computers, 28, 584–589.
Belia, S., Fidler, F., Williams, J., & Cumming, G. (2005). Researchers misunderstand confidence intervals and standard error bars. Psychological Methods, 10, 389–396.
Blouin, D. C., & Riopelle, A. J. (2005). On confidence intervals for within-subject designs. Psychological Methods, 10, 397–412.
Cleveland, W. S. (1985). The elements of graphing data. New York: Chapman & Hall.
Cousineau, D. (2005). Confidence intervals in within- subject designs: A simpler solution to Loftus and Masson’s method. Tutorials in Quantitative Methods for Psychology, 1, 42–45.
Cumming, G., & Finch, S. (2005). Inference by eye: Confidence intervals, and how to read pictures of data. American Psychologist, 60, 170–180.
Dienes, Z. (2008). Understanding psychology as a science: An introduction to scientific and statistical inference. Basingstoke: Palgrave Macmillan.
Fidler, F., & Loftus, G. (2009). Why figures with error bars should replace p values: Some conceptual arguments and empirical demonstrations. Zeitschrift für Psychologie, 217, 27–37.
Goldstein, H., & Healy, M. J. R. (1995). MJR: The graphical presentation of a collection of means. Journal of the Royal Statistical Society: Series A, 158, 175–177.
Hollands, J. G., & Jarmasz, J. (2010). Revisiting confidence intervals for repeated-measures designs. Psychonomic Bulletin & Review, 17, 135–138.
Hox, J. J. (2010). Multilevel analysis: Techniques and applications (2nd ed.). Mahwah: Erlbaum.
Jarmasz, J., & Hollands, J. G. (2009). Using confidence intervals in repeated-measures designs: The number of observations principle. Canadian Journal of Experimental Psychology, 63, 124–138.
Kelley, K., Maxwell, S. E., & Rausch, J. R. (2003). Obtaining power or obtaining precision: Delineating methods of sample size planning. Evaluation & the Health Professions, 26, 258–287.
Keselman, H. J., Algina, J., & Kowalchuk, R. K. (2001). The analysis of repeated measures designs: A review. British Journal of Mathematical and Statistical Psychology, 54, 1–20.
Kirk, R. E. (1995). Experimental design (3rd ed.). Belmont: Brooks/Cole.
Loftus, G. R. (2001). Analysis, interpretation, and visual presentation of experimental data. In J. Wixted & H. Pashler (Eds.), Stevens’ handbook of experimental psychology: Vol. 4. Methodology in experimental psychology (3rd ed., pp. 339–390). New York: Wiley.
Loftus, G. R., & Masson, M. E. J. (1994). Using confidence intervals in within-subject designs. Psychonomic Bulletin & Review, 1, 476–490.
Masson, M. E. J., & Loftus, G. R. (2003). Using confidence intervals for graphically based data interpretation. Canadian Journal of Experimental Psychology, 57, 203–220.
Mitzel, H. C., & Games, P. A. (1981). Circularity and multiple comparisons in repeated measures designs. British Journal of Mathematical and Statistical Psychology, 34, 253–259.
Morey, R. D. (2008). Tutorials in Quantitative Methods for Psychology, 4, 61–64.
Moses, L. E. (1987). Graphical methods in statistical analysis. Annual Review of Public Health, 8, 309–353.
Pinheiro, J., Bates, D., DebRoy, S., Sarkar, D., & the R Core Team (2009). nlme: Linear and nonlinear mixed effects models. R package version 3.1-92.
R Development Core Team. (2009). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. Available at www.R-project.org.
Rosenthal, R., Rosnow, R. L., & Rubin, D. B. (2000). Contrasts and correlations in behavioral research. New York: Cambridge University Press.
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225–237.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological Bulletin, 57, 416–428.
Schenker, N., & Gentleman, J. F. (2001). On judging the significance of differences by examining the overlap between confidence intervals. The American Statistician, 55, 182–186.
Searle, S. R., Casella, G., & McCulloch, C. E. (1992). Variance components. New York: Wiley.
Uppal, A. (2006). Can children effectively recognize pride from body posture or facial expression? Unpublished BSc. psychology research project. Nottingham Trent University, Nottingham, U.K.
Warnes, G. R., Bolker, B., Lumley, T., & Johnson, R. C. (2009). gmodels: Various R programming tools 1397 for model fitting. R package version 2.15.0. Available at http://CRAN.R-project.org/package=gmodels.
Wilcox, R. R., & Keselman, H. J. (2003). Modern robust data analysis methods: Measures of central tendency. Psychological Methods, 8, 254–274.
Wilkinson, L., & the Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54, 594–604.
Wright, D. B. (2007). Graphing within subject confidence intervals (WSCI) using SPSS and S-Plus. Behavior Research Methods, 39, 82–85.
Author note
The author thanks Andy Fugard, Ken Kelley, Gregory Francis, and two anonymous reviewers for providing constructive comments on previous drafts of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.3758/s13428-013-0347-9.
Appendix
Appendix
This code tricks SPSS into plotting 95% confidence intervals for the Loftus and Masson (1994) free recall data with the Cousineau–Morey approach. The first set of commands computes the required confidence level to obtain a 95% CI, using the normalized scores for n per level = 10 and J = 3 levels. To adjust any of these values, just edit the appropriate value of the input (0.95, 3, or 10).

This should return the target confidence level (97.83%) as a variable in a new data view window and return the value to the output window (along with the inputs).
At this point, open or make active the SPSS data file  . The next set of commands calculates the normalized data (and is adapted from Cousineau, 2005).
. The next set of commands calculates the normalized data (and is adapted from Cousineau, 2005).

To obtain the 95% Cousineau–Morey intervals, either use the one-sample T-TEST procedure or plot the CIs using 97.83% as the nominal confidence level.

These intervals match those of the call  to the
to the  R function provided in the supplementary materials to about three decimal places.
R function provided in the supplementary materials to about three decimal places.
Rights and permissions
About this article
Cite this article
Baguley, T. Calculating and graphing within-subject confidence intervals for ANOVA. Behav Res 44, 158–175 (2012). https://doi.org/10.3758/s13428-011-0123-7
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-011-0123-7


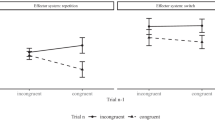








 function in R. SPSS users can restructure the data set using the
function in R. SPSS users can restructure the data set using the  command.
command. will download and install the package from an online repository (and you may be prompted to select one if you have not previously installed a new package).
will download and install the package from an online repository (and you may be prompted to select one if you have not previously installed a new package). function or
function or  . The call
. The call  or
or  brings up information about the graphical parameters.
brings up information about the graphical parameters.