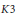Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Top, Jaap
and
Zeeuw, Frank De
2009.
Explicit Elliptic $K3$ Surfaces with Rank 15.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 5,
Schütt, Matthias
Shioda, Tetsuji
and
van Luijk, Ronald
2010.
Lines on Fermat surfaces.
Journal of Number Theory,
Vol. 130,
Issue. 9,
p.
1939.
ELSENHANS, ANDREAS-STEPHAN
and
JAHNEL, JÖRG
2011.
On the computation of the Picard group for K3 surfaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 151,
Issue. 2,
p.
263.
Salgado, Cecilia
2012.
On the rank of the fibers of elliptic K3 surfaces.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 43,
Issue. 1,
p.
7.
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2012.
Kummer surfaces and the computation of the Picard group.
LMS Journal of Computation and Mathematics,
Vol. 15,
Issue. ,
p.
84.
Hassett, Brendan
and
Várilly-Alvarado, Anthony
2013.
Failure of the Hasse principle on general surfaces.
Journal of the Institute of Mathematics of Jussieu,
Vol. 12,
Issue. 4,
p.
853.
Garbagnati, Alice
2013.
Elliptic K3 Surfaces with Abelian and Dihedral Groups of Symplectic Automorphisms.
Communications in Algebra,
Vol. 41,
Issue. 2,
p.
583.
Schütt, Matthias
2013.
Arithmetic and Geometry of K3 Surfaces and Calabi–Yau Threefolds.
Vol. 67,
Issue. ,
p.
71.
Poonen, Bjorn
Testa, Damiano
and
van Luijk, Ronald
2015.
Computing Néron–Severi groups and cycle class groups.
Compositio Mathematica,
Vol. 151,
Issue. 4,
p.
713.
KUMAR, ABHINAV
and
KUWATA, MASATO
2017.
ELLIPTIC K3 SURFACES ASSOCIATED WITH THE PRODUCT OF TWO ELLIPTIC CURVES: MORDELL–WEIL LATTICES AND THEIR FIELDS OF DEFINITION.
Nagoya Mathematical Journal,
Vol. 228,
Issue. ,
p.
124.
Várilly-Alvarado, Anthony
2017.
Geometry Over Nonclosed Fields.
p.
197.
Fisher, Tom
2020.
Explicit moduli spaces for congruences of elliptic curves.
Mathematische Zeitschrift,
Vol. 295,
Issue. 3-4,
p.
1337.
Gong, Cheng
and
Xu, Wan-Yuan
2020.
On the Mordell–Weil rank of a surface fibration.
Communications in Algebra,
Vol. 48,
Issue. 2,
p.
724.
Kimura, Yusuke
2021.
F-theory models with 3 to 8 U(1) factors on K3 surfaces.
International Journal of Modern Physics A,
Vol. 36,
Issue. 17,
p.
2150125.
Costa, Edgar
and
Sertöz, Emre Can
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
293.
Gillibert, Jean
and
Levin, Aaron
2022.
Descent on elliptic surfaces and arithmetic bounds for the Mordell–Weil rank.
Algebra & Number Theory,
Vol. 16,
Issue. 2,
p.
311.